引言
大涡模拟 是模拟和预测非定常湍流的有效工具,它的基本思想是数值求解大涡的运动,而采用物理模型模拟小涡对大涡的影响. 比较而言,直接数值模拟 虽然可以模拟非定常湍流,但其巨大的计算量导致难以用于工程实际. 雷诺平均 方法的计算量较小,因此常用于工程问题[1 ] ,但它难以用于预测大涡运动的非定常特性. 随着计算机的发展,大涡模拟已经越来越多地被应用于科学研究和工程设计[2 ,3 ,4 ,5 ] . 当大涡模拟用于壁湍流时,由于壁面会引入正比于壁面距离的新的尺度,因此在壁面附近,大涡模拟又分为解析壁面 层(wall-resolved)的大涡模拟和模化壁面层(wall-modeled)的大涡模拟[6 ,7 ] . 解析壁面层的网格尺度与黏性长度同量级,模化壁面层的网格尺度与边界层厚度同量级,因此模化壁面层的大涡模拟所需的网 格量远小于解析壁面层的网格量. 例如,在一个计算机翼绕流的算例中,当雷诺数 Re = 1 0 9 [8 ] 因此,模化壁面层的大涡模拟在工程中有重要意义.
本文详细讨论了大涡模拟壁模型的特点和最新发展,内容安排如下:在第1节 讨论了大涡模拟的壁模型. 首先介绍了壁模型的基本思想和分类,然后介绍了平衡层壁模型,最后介绍了非平衡壁模型和双层模型的最新发展. 在第2节, 介绍了周期山状流的模化壁面层的大涡模拟和平衡层壁模型的应用细节,并与先前的计算和实验结果进行了比较. 第3节对本文的内容进行了总结和展望.
1 壁模型
壁面附近湍流结构的特征尺度正比于其与壁面间的距离. 如果完全解析近壁湍流结构,大涡模拟所需的计算量与直接数值模拟相当. 解析壁面层的大涡模拟大部分的网格用于解析近壁流动. Re > 1 0 6 [9 ,10 ] . 壁面附近的流动常满足特定的规律并趋于形成自维持过程[11 ,12 ] . 近壁湍流的上述特性使得可以采用简化的方法或模型刻画近壁流动,常用的简化方案有雷诺平均与大涡模拟混合方法[13 ,14 ,15 ] 和壁模型[9 -10 ,16 ] . 本文介绍采用壁模型简化近壁流动的方案.
Sagaut[11 ] 将大涡模拟壁模型分为4类:高阶边界条件(high-order boundary conditions),壁面应力模型(wall-stress models),离面边界条件(off-wall boundary conditions) 和确定性最小边界层单元模拟(deterministic minimal boundary-layer unit simulation),其中壁面应力模型的应用最为广泛.
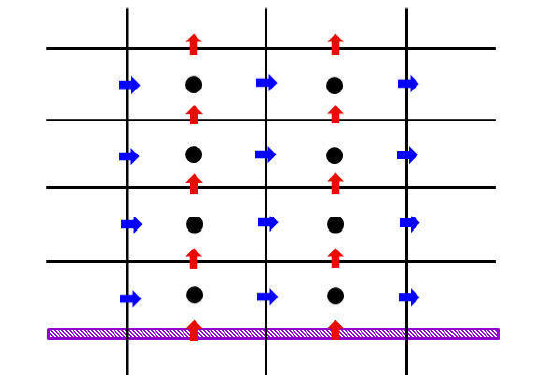
壁面应力模型可以在较粗的网格上保证近壁的动量守恒,从而得到正确的速度分布. 以图1 中的不可压槽道湍流为例,控制方程为不可压缩流动的Navier-Stokes(NS)方程
$\dfrac{\partial u_i }{\partial t} + \dfrac{\partial u_i u_j }{\partial x_j } = -\dfrac{1}{\rho }\dfrac{\partial p}{\partial x_i } + \nu \dfrac{\partial ^2u_i }{\partial x_j \partial x_j } -\dfrac{1}{\rho }\dfrac{\partial P}{\partial x_i }\delta _{1i} (1)$
$\dfrac{\partial u_i }{\partial x_i } = 0 (2)$
其中, u i i = 1,2 , 3 p P ρ ν
$\dfrac{\partial \bar {u}_i }{\partial t} + \dfrac{\partial \bar {u}_i \bar {u}_j }{\partial x_j } = - \dfrac{1}{\rho }\dfrac{\partial \bar {p}}{\partial x_i } + \nu \dfrac{\partial ^2\bar {u}_i }{\partial x_j \partial x_j } + \dfrac{\partial \tau _{ij} }{\partial x_j } - \dfrac{1}{\rho }\dfrac{\partial P}{\partial x_i }\delta _{1i} $(3)
$\dfrac{\partial \bar {u}_i }{\partial x_i } = 0 (4)$
图1 湍流大涡模拟区域与壁模型示意图. 边界附近的网格不足以解析近壁流动结构时,常用的有限差分算子得到的黏性应力项并不 是壁面切应力的正确值. 壁模型可以在较粗的网格上保证近壁的动量守恒,从而得到正确的速度分布(根据Piomelli和Balaras[9 ] 的图2 修改而来)
Fig. 1 Diagrammatic sketch of the LES region and the wall-model. If meshes near the wall is too coarse to resolve the flow structure, the viscous stress obtained by the usual finite difference operator is not correct. Wall-models can guarantee the momentum conservation on coarse meshes near the wall, obtaining correct velocity profiles (modified based on the Fig.2 of Ref.[9])
其中,顶标‘ ¯ τ ij = u ̅ i u ̅ j - u i u j ¯
为不失一般性, 以Schumann[17 ] 提供的方法为例在图2 所示的网格上离散动量方程(3)
$ \dfrac{\partial \bar {u}_i }{\partial t} + {\rm D}_j \left( {\bar {u}_i \bar {u}_j } \right) = - {\rm D}_i \left( {\dfrac{\bar {p}}{\rho }} \right) + {\rm D}_j \left( {\nu \dfrac{\partial \bar {u}_i }{\partial x_j }} \right) + {\rm D}_j \tau _{ij} - {\rm D}_i \left( {\dfrac{P}{\rho }} \right)\delta _{1i} (5) $
其中, D ν ∂ u ̅ 1 / ∂ x 2
图2 交错网格与边界示意图
Fig. 2 Schematic of the staggered mesh and the boundary
Schumann[17 ] 提出了一种根据壁面律计算壁面切应力的模型(常被称为平衡层模型[6 ] ),该模型从已解析的流场中构造瞬时壁面应力边界条件
$\tau _{\rm w} = \dfrac{\left. u \right|_1 }{\left. {\left\langle u \right\rangle } \right|_1 }\left\langle {\tau _{\rm w} } \right\rangle (6) $
其中, u 1 u 1 τ w [17 ] 利用恒定压力梯度槽道和管道流动的特点给出平均壁面应力 τ w [17 ] 所给出的壁面应力模型的一个主要缺点是需要事先知道平均壁面应力. 克服这一缺点的一种方案是通过近壁的速度分布反推壁面切应力[18 ] ,即求解如下方程
$\dfrac{\left\langle u \right\rangle \left( y \right)}{u_\tau } = \dfrac{1}{\kappa }\ln \left( {\dfrac{yu_\tau }{\nu }} \right) + C (7)$
其中, u τ = τ w / ρ κ C C ≈ 5.5 . 通过已解析的流动可得到对数区距壁面 y u . 方程(7)中的唯一未知量为 u τ τ w = ρ u τ 2 .
Werner-Wengle模型[19 ] (简称WW模型)采用瞬时速度代替平均速度,并采用线性律与幂律的匹配形式近似表示壁面速度分布,得到了壁面切应力与已解析的近壁流场速度的解析表达式. 与方程(7)相比,WW模型有两个优点:第一,可以通过瞬时速度求得瞬时壁面切应力;第二,避免了求解含有对数函数的超越方程. WW模型的速度剖面为
$u^ + = \begin{cases} {y^ + } , & {y^ + \leqslant y_{\rm C}^ + } \\ {A\left( {y^ + } \right)^B} , & {y^ + > y_{\rm C}^ + } \end{cases} (8)$
其中, A = 8.3 B = 1 / 7 y C + = A 1 / 1 - B u + = u / u τ y + = y u τ / ν .
Inagaki等[20 ] 在WW模型的双层速度形式基础上引入了缓冲层的影响并通过修正后的三层速度匹配形式改进了计算结果
$u^ + = \begin{cases} {y^ + } ,& { y^ + \leqslant y_{\rm C1}^ + } \\ {A_1 \left( {y^ + } \right)^{B_1 }} , & {y_{\rm C1}^ + < y^ + \leqslant y_{\rm C2}^ + } \\ {A_2 \left( {y^ + } \right)^{B_2 }} , & {y^ + > y_{\rm C2}^ + } \end{cases} (9) $
其中, A 1 = 2.7 A 2 = 8.6 B 1 = 1 / 2 B 2 = 1 / 7 y C 1 + = A 1 1 / 1 - B 1 y C 2 + = A 2 / A 1 1 / B 1 - B 2 .
Breuer和Rodi[21 ] 在对数律中提出三层速度匹配形式,分段表示出线性律、缓冲层和对数律的速度剖面
$ u^ + = \begin{cases} {y^ + } , & {y^ + \leqslant 5} \\ {A\ln \left( {y^ + } \right) + B} , & {5 < y^ + \leqslant 30} \\ {\kappa ^{ - 1}\ln \left( {Ey^ + } \right)} , & {y^ + > 30} \end{cases} (10) $
其中, E = 9.8 A = κ - 1 ln 30 E - 5 / ln 6 B = 5 - A ln 5 .
上述壁面应力模型均由近壁的瞬时速度确定壁面应力. 这一做法的物理基础是对数律区的速度与壁面应力相关的实验现象[22 ] . 这一物理基础隐含了上述模型中所用到的已解析的近壁流场速度位于对数律区,即:距壁面的第一层网格不超过对数律区. 值得注意的是,这种基于统计平均的速度分布又要求近壁流动的网格要适当的粗,以保证单位网格区域内包含足够数量的小尺度结构[9 ] . 实际计算中常取距壁面的第一层网格位于对数律区或黏性子区的上层. 上述壁面应力模型没有考虑边界层内的相干结构对壁面应力和速度脉动的影响,而边界层内的倾斜结构以及下扫和喷射过程都会影响壁面应力和速度脉动的关联. Piomelli等[23 ] 通过引入流向距离参数考虑倾斜结构引起的壁面切应力与近壁速度之间的滞后现象.
壁面应力模型的基础是近壁平均速度分布的壁面律,但普适的壁面律在具有逆压梯度的流动中并不存在[24 ] . 尽管如此,这些模型仍被广泛地应用于建筑物绕流、风场以及大气边界层等高雷诺数复杂壁湍流的大涡模拟[9 ,10 ] ,并且常可得到合理的结果,尤其是流动的平均量. Larsson等[25 ] 对这一现象的解释为:(1)壁面应力模型仅模化了边界层内区的部分流动(约占边界层厚度的20%),大涡模拟可以解析80%边界层厚度内的非平衡效应;并且未解析的20%近壁流动的时间尺度远小于已解析的流动尺度(因流动的时间尺度与壁面距离成正比);(2)逆压梯度较大的流动区域往往对应于对流项较大的区域,两者对壁面应力的影响可相互抵消. 但同时,也有工作表明平衡律模型难以准确计算分离流动的壁面摩擦力[10 ] .
Breuer等[26 ] 从边界层方程出发,考虑了压力梯度的非平衡效应,对WW模型进行了推广. 该方法通过WW模型的幂律速度剖 面构造人工黏性,并通过统计估计定义黏性子层的相对厚度,在周期山状流的数值模拟中准确计算了流动的分离与壁面摩擦力. Duprat等[27 ] 在近壁流动的控制方程中直接考虑了流向压力梯度的非平衡效应,同时以流向压力梯度和壁面摩擦力为特征量, 引入近壁流动的混合特征速度,并以此对壁面单位进行了重新标度. 进一步地,Duprat等[27 ] 依据此混合速度提出了一种近壁涡黏系数衰减的新形式,从而引入了压力梯度对速度剖面和壁面应力 的影响. 相比于仅考虑平衡效应的壁面模型,定义混合速度有效地克服了流动分离点附近的奇异性,并有效地反映了流向压力梯度对流动的影响. 该壁模型准确模拟了周期山状流,尤其在流动的逆压区取得较好的预测结果,数值结果表明在非平衡壁模型中同时考虑了压力梯度和雷诺应力具有重要意义.
Yang等[28 ] 同时考虑了近壁流动的压力梯度效应以及局部加速度和对流效应,并提出积分型壁模型. 该模型首先假设近壁速度剖面由线性过渡为对数函数的多参数形式,并引入线性扰动对平衡层壁面律进行了推广;然后通过匹配条件以及积分边界层方程的物理约束,重构壁面流动的速度分布形式,并由此确定壁面摩擦力. 相比于平衡层模型,该模型同时考虑了控制方程中各非平衡项;相比于双层模型(下文将详述),该模型避免了直接求解边界层方程,因此该模型具有多物理和实现简单的优点,迅速引起了广泛关注.
Nicoud等[29 ] 提出了通过最优控制理论来确定壁面切应力的方法. 该方法将计算出的平均速度剖面与目标平均速度剖面的偏差作为优化目标,采用一个时间步长内的次优控制策略可以在较粗的网格上得到较为准确的壁面切应力,并以此约束外区大涡模拟达到最优解. 但是该方法在每个时间步都需要大量的迭代来完成优化过程,因此它的成本比在相同的网格上使用显式壁面应力模型大20倍. 此外,该方法还必须提供目标平均速度剖面用来确定目标函数. 为了克服这些缺点,Nicoud等[29 ] 提出了线性随机估计形式的壁面应力模型,该模型可以通过局部速度场显式预测壁面切应力,其中的模型系数通过次优控制策略得到的数据确定. 槽道湍流数值模拟的结果表明由该方法推导出的壁模型可以在较粗的网格上准确预测高雷诺数流动的平均速度剖面. 最近,Bae等[30 ,31 ,32 ,33 ] 提出了滑移边界条件修正壁面应力边界条件可能引起的对数区速度匹配问题.
另外一种提供壁面应力边界条件的模型是双层模型(two-layer model). 这种模型通过在壁面附近嵌入一套细网格并在细网格上求解简化的流动方程为大涡模拟提供应力边界条件[34 ] ,近壁流动的简化方程常取为雷诺平均后的边界层方程
$ \dfrac{\partial u_i }{\partial t} + \dfrac{\partial u_i u_j }{\partial x_j } = - \dfrac{1}{\rho }\dfrac{\partial p}{\partial x_i } + \dfrac{\partial }{\partial x_2 }\left[ {\left( {\nu + \nu _t } \right)\dfrac{\partial u_i }{\partial x_2 }} \right] , \ \ {i = 1,3} $(11)
$ \dfrac{\partial u_2 }{\partial x_2 } = - \dfrac{\partial u_1 }{\partial x_1 } -\dfrac{\partial u_3 }{\partial x_3 } (12)$
其中压力项通过外流得到,湍流涡黏 ν t
$\dfrac{\nu _t }{\nu } = \kappa y^ + \left( {1 - {\rm e}^{ - {y^ + } /A}} \right)^2 (13)$
其中 A = 19 .
双层模型[34 ] 用于近壁平衡的流动时Karman系数 κ [35 ] 提出了动态Karman系数的修正方法,使得第一层大涡模拟网格上的湍流涡黏 ν t ν S GS
$\hat {\kappa } = \dfrac{\left\langle {\nu _{\rm SGS} } \right\rangle }{\nu \left\langle {y_{\rm w}^ + \left({1 - {\rm e}^{ - {y_{\rm w}^ + } /A}} \right)^2} \right\rangle } (14)$
其中, y w + [35 ] 将该方法用于机翼绕流中,准确预测了流动分离和再附区. Kawai和Larsson[36 ] 认为,Karman系数 κ κ ̂ κ ̂ . Kawai和Larsson[36 ] 假设Karman系数 κ [37 ] 根据需要被模化的雷诺应力加上可解应力的和为通过Karman系数标准值0.41得到的总应力, 也得到了随壁面法向变化的动态Karman系数 κ .
由上可以看到,双层模型比基于壁面律的壁面应力模型更易考虑非平衡效应,但其应用过程也相应 比较复杂. 与双层模型相 关的综述或介绍可参见文献[9 ,38 -40 ] .
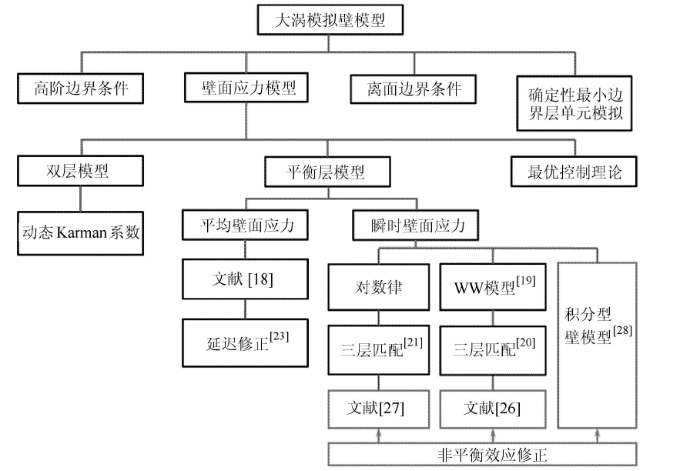
本节内容所提到的大涡模拟壁模型关系如图3 所示. 本文主要介绍了壁面应力模型中的平衡层模型和双层模型. 平衡层模型假设 速度剖面的形式(例如对数律或WW模型中的幂律),从而可以通过瞬时近壁速度求得瞬时壁面切应力. 在此基础上,出现了多种考虑非平衡效应的修正方法. 双层模型通过在近壁细网格上求解简化的流动方程得到壁面切应力,并通过动态方法调整湍流涡黏中的Karman系数来考虑非平衡效应.
图3 本文介绍的大涡模拟中的壁模型,其中壁面应力模型的应用最为广泛. 它主要包括平衡层模型和双层模型. 平衡层模型可以 通过近壁速度求得壁面切应力,双层模型通过在近壁细网格上求解简化的流动方程得到壁面切应力. 在平衡层模型的基础上,考虑非平衡效应的修正方法可以用于非平衡湍流
Fig. 3 Wall-models for LES of wall-bounded turbulence. Wall-stress models are widely used in LES. The equilibrium models and the two-layer models are the two main branches of the wall-stress models. The equilibrium models compute the wall-stress based on the equilibrium boundary layer near the wall. The two-layer models compute the wall-stress by solving the simplified equations near the wall. The improved versions of the equilibrium models have the capability of accounting for the non-equilibrium effects
2 周期山状流的模化壁面层的大涡模拟
2.1 周期山状流的大涡模拟方程
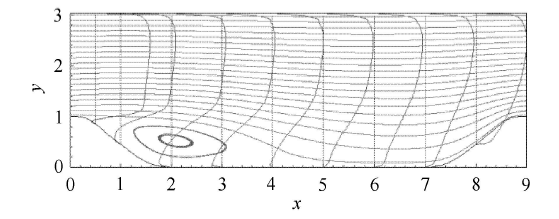
周期山状流是ERCOFTAC/IAHR(欧洲湍流与燃烧研究机构)设计的LES的测试算例,被广泛用于数值方法和湍流模型的研究[41 ,42 ,43 ,44 ] . 该算例所用的工况为槽道中周期性放置山状障碍,其中山的高度为 h 9 h 3.035 h 4.5 h . 雷诺数( Re = U b h / ν ) 为10 595,其中 U b h U b 图4 给出了周期山状流平均速度的流线以及不同流向位置处的平均流向速度剖面.
图4 周期山状流平均速度的流线以及不同流向位置处的平均流向速度剖面
Fig. 4 The streamlines and the profiles of the mean streamwise velocities at different streamwise locations
为封闭大涡模拟方程中的亚格子应力项,通常使用不可压缩湍流的涡黏假设
$\tau _{ij} = 2\nu _{\rm SGS} \bar {S}_{ij} + \dfrac{1}{3}\delta _{ij} \tau _{kk} (15)$
其中, S ̅ ij = ∂ u ̅ i / ∂ x j + ∂ u ̅ j / ∂ x i / 2 ν S GS
在采用了上面的涡黏假设后,大涡模拟的动量方程如下
$ \dfrac{\partial \bar {u}_i }{\partial t} + \dfrac{\partial \bar {u}_i \bar {u}_j }{\partial x_j } = - \dfrac{1}{\rho }\dfrac{\partial \bar {p}}{\partial x_i } + \dfrac{\partial }{\partial x_j }\Bigg[ \left({\nu + \nu _{\rm SGS} } \right) \cdot \\ \left( {\dfrac{\partial \bar {u}_i }{\partial x_j } +\dfrac{\partial \bar {u}_j }{\partial x_i }} \right)\Bigg] - \dfrac{1}{\rho }\dfrac{\partial P}{\partial x_i}\delta _{1i} (16)$
需要得到涡黏系数的模型才能求解方程(16). Smagorinsky涡黏模型[45 ] 是大涡模拟中常用的模型之一,它的涡黏系数为
ν S GS = C s 2 Δ ̅ 2 S ̅ ( 17 )
其中, S ̅ = 2 S ̅ ij S ̅ ij Δ ̅ C s 2 C s 2
为了解决这个问题,Germano等[46 ] 发展了确定系数 C s 2 Δ ̅ Δ ̅ ∧ . 同时采用该单元与相邻单元内物理量的简单平均得到二次滤波以后的量. 在使用滤波宽度 Δ ̅ τ ij Δ ̅ ∧ T ij τ ij T ij
$\tau _{ij} = \bar {u}_i \bar {u}_j - \overline {u_i u_j } (18)$
$ T_{ij} = {\mathop{\bar {u}}\limits^{ \wedge}}_i {\mathop{\bar {u}}\limits^{ \wedge}}_j - \widehat{\overline {u_i u_j } } (19)$
从而可以得到Germano恒等式
L ij = u ̅ ∧ i u ̅ ∧ j - u ̅ i u ̅ j ̂ = T ij - τ ∧ ij (20)
其中, u ̅ ∧ i u ̅ ∧ j - u ̅ i u ̅ j ̂
根据Smagorinsky模型,滤波宽度 Δ ̅
$\tau _{ij} - \dfrac{1}{3}\delta _{ij} \tau _{kk} = 2C_{\rm s}^2 \bar {\varDelta }^2\left| \bar {S}\right|\bar {S}_{ij} (21)$
同样地,滤波宽度 Δ ̅ ∧
$T_{ij} - \dfrac{1}{3}\delta _{ij} T_{kk} = 2C_s^2 {\mathop{\bar {\varDelta^2 }}\limits^{ \wedge}}\left|{\mathop{\bar {S}}\limits^{ \wedge}} \right|{\mathop{\bar {S}}\limits^{ \wedge}}_{ij} (22)$
代入Germano恒等式,并令
$M_{ij} = \left( {\mathop{\bar {\varDelta^2}}\limits^{ \wedge}} / \bar {\varDelta }^2 \right)\left|{\mathop{\bar {S}}\limits^{ \wedge}} \right|{\mathop{\bar {S}}\limits^{ \wedge}}_{ij} - \widehat{\left|\bar {S} \right|\bar {S}_{ij} } (23)$
可以得到
$L_{ij} - \dfrac{1}{3}\delta _{ij} L_{kk} = 2C_{\rm s}^2 \bar {\varDelta }^2M_{ij} (24)$
上式是超定方程,可以采用最小二乘法求解[47 ]
$C_{\rm s}^2 \bar {\varDelta }^2 = \dfrac{1}{2}\dfrac{L_{ij} M_{ij} }{M_{kl} M_{kl} } (25)$
需要注意的是,根据上式计算得到的系数 C s 2
$C_{\rm s}^2 \bar {\varDelta }^2 = \dfrac{1}{2}\dfrac{\left\langle {L_{ij} M_{ij} } \right\rangle _z}{\left\langle {M_{kl} M_{kl} } \right\rangle _z } (26)$
其中, z
在 数值模拟中,下壁面设置为无滑移边界条件,流向与展向设置为周期边界条件,上壁面的切应力边界条件由壁模型提供. 时间推进采用分步法,对流项的时间推进采用显式的两步Adams-Bashforth格式,黏性项采用Crank-Nicholson格式. 流场采用非结构网格离散,方程中的空间导数采用有限体积方法离散. 非结构网格可以采用任意形状的单元,因此能够很好地模拟复杂几何边界. 尤其是在非结构网格上结合有限体积方法,可以使计算程序具有很强的通用性. 为了保持数值计算的精度和稳定性, 使用了基于离散动能守恒原理的非结构网格上的离散方法[48 ] . 该方法在计算区域中不产生非物理的能量源,从而可以保持大涡模拟的精度和预测能力. 压力Poisson方程采用代数多重网格方法求解,代数多重网格的求解器为Hypre软件包中的BoomerAMG.
2.2 周期山状流大涡模拟的壁模型
本节阐述在计算中采用WW模型 (式(8)) 的主要思路,即如何由近壁速度确定壁面切应力.
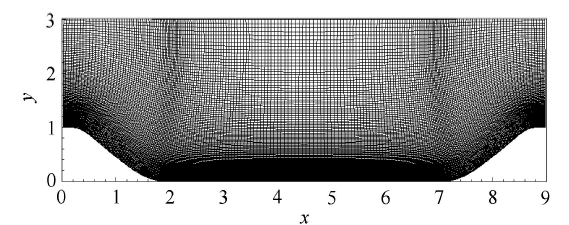
采用 与ERCOFTAC数据库中文献[49 ,50 ] 相同的计算网格:其中流向、法向和展向的网格数目分别为197, 129和186. 需要注意的是, 文献[49 ,50 ] 使用基于结构网格的流场求解器,而本文使用基于非结构网格的流场求解器, 因此该网格预先被处理成非结构网格的形式. 图5 画出了垂直于展向的某一截面上的网格分布,下壁面近壁网格的特征尺度满足
y 1 + < 2 (27)
其中,上标“+”表示用黏性长度做无量纲化, y 1
y 1 + ∈ [ 12,17 ] (28)
可以看到上壁面附近网格尺度不能够解析壁面层,因此需要在上壁面使用壁模型.
图5 周期山状流的大涡模拟所用的网格截面
Fig. 5 A two-dimensional slice of the grid used for LES of the flows over periodic hills
本文使用的壁模型是WW模型(式(8)). 在应用中通常采用单元积分的形式,即
U p u τ = 1 Δ y + ∫ 0 Δ y + u + ( y + ) d y + ( 29 )
其中, U p Δ y + = Δ y u τ / ν Δ y u τ
根据WW模型(式(8)),如果近壁速度满足
$\left| {U_{\rm p} } \right| \leqslant \dfrac{\nu }{2\Delta y}A^{\tfrac{2}{1 - B}} (30)$
则第一层网格全部在线性底层. 此时,壁面切应力可以表示为
$\left| {\tau _{\rm w} } \right| = \rho \dfrac{2\nu \left| {U_{\rm p} } \right|}{\Delta y} (31)$
如果近壁速度满足
$\left| {U_{\rm p} } \right| > \dfrac{\nu }{2\Delta y}A^{\tfrac{2}{1 - B}} (32)$
则第一层网格单元内的速度部分在线性层部分在幂律层. 此时,壁面切应力可以表示为
$\left| {\tau _{\rm w} } \right| = \rho \left[ {\dfrac{1 - B}{2}A^{\tfrac{1 + B}{1 - B}}\left( {\dfrac{\nu }{\Delta y}} \right)^{1 + B} + \dfrac{1 + B}{A}\left({\dfrac{\nu }{\Delta y}} \right)^B\left| {U_{\rm p} } \right|} \right]^{\tfrac{2}{1+ B}} (33)$
由此,根据WW模型得到了壁面切应力与近壁速度间的解析关系. 根据Schumann[17 ] 的假设,近壁附近的瞬时切向速度 和壁面切应力同向. 由此在计算中,上述表达式中壁面切应力 τ w U p
2.3 计算结果
本文采用动态Smagorinsky模型(以下简写为DSM)作为大涡模拟的亚格子模型,并且在上壁面使用WW模型. 当流动达到统计定常 的状态后统计时长为 500 h / U b .
图4 画出了平均流场的流线,从中可以看出流动分离、再附和回流区等分离流的物理特征. 流动分离点在 x = 0.2 x = 4.6 [49 ,50 ] 的结果吻合.
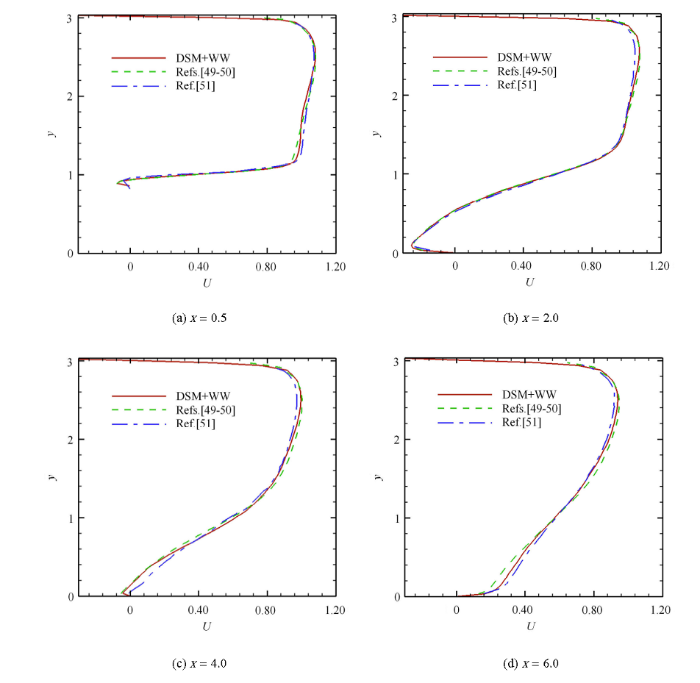
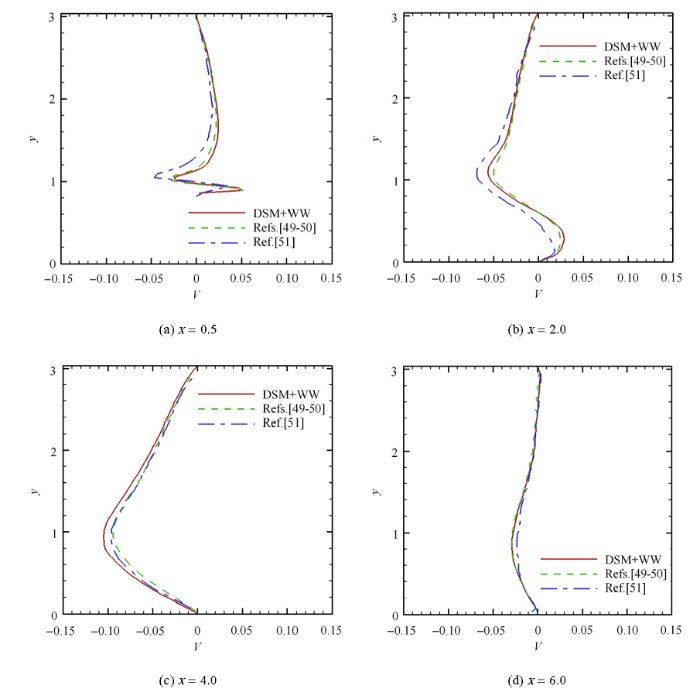
本文在4个截面处比较了计算的平均速度与文献[49 ,50 ]的计算结果以及文献[51 ] 的实验结果,这4个截面分别是位于流动分离点 附近的 x = 0.5 x = 2.0 x = 4.0 x = 6.0 . 图6 对比了平均流向速度 U 图7 对比了平均法向速度 V 49 ,50 ]的计算结果以及文献[51 ] 的实验结果 吻合很好. x = 0.5 图6 (a)所示. 此外,流速在山顶高度附近快速增加,这说明存在流动分离形成的强剪切层. x = 2.0 x = 0.5 图6 (b)所示. x = 4.0 图6 (c)所示. x = 6.0 图6 (d)所示. 此外,图7 (c)和图7 (d)表明 x = 4.0 x = 6.0
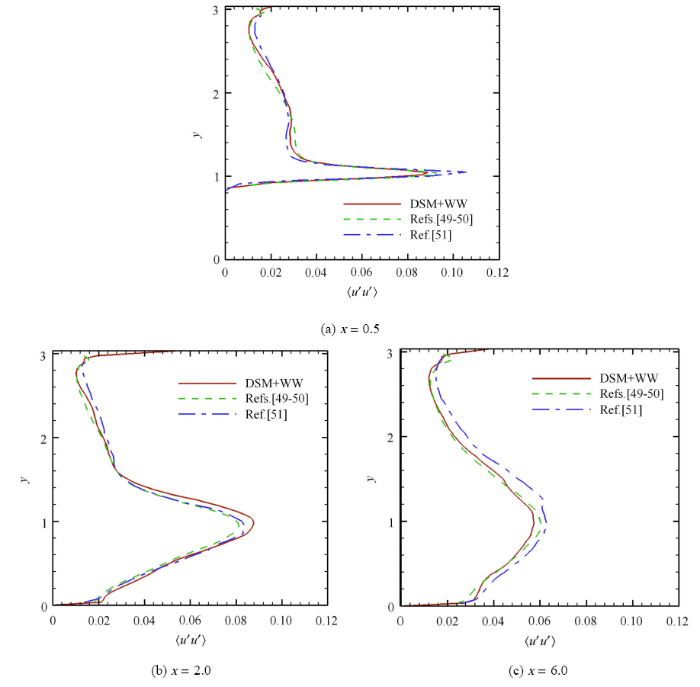
进一步地比较 x = 0.5 x = 2.0 x = 6.0 图8 比较了流向脉动速度的二阶统计量 u ' u ' 图9 比较了法向脉动速度的二阶统计量 v ' v ' 图10 比较了雷诺应力 u ' v ' . 本文的结果与文献[49 ,50 ] 的计算结果以及文献[51 ] 的实验结果吻合很好. x = 0.5 图8 (a)和图10 (a)所示. 从图8 (b)、图9 (b)以及图10 (b)可以看出,由于存在剪切, x = 2.0 图6 (d)表明 x = 6.0 图8 (c), 图9 (c)以及图10 (c)可以看出, x = 6.0 x = 2.0
图6 周期山状流的流向平均速度剖面的比较
Fig. 6 The profiles of the mean streamwise velocities
图7 周期山状流的法向平均速度剖面的比较
Fig. 7 The profiles of the mean wall-normal velocities
图8 周期山状流的流向速度脉动方差的比较
Fig. 8 The variance of streamwise velocities
图9 周期山状流的法向速度脉动方差的比较
Fig. 9 The variance of wall-normal velocities
图10 周期山状流的雷诺应力的比较
Fig. 10 The profiles of Reynolds stresses
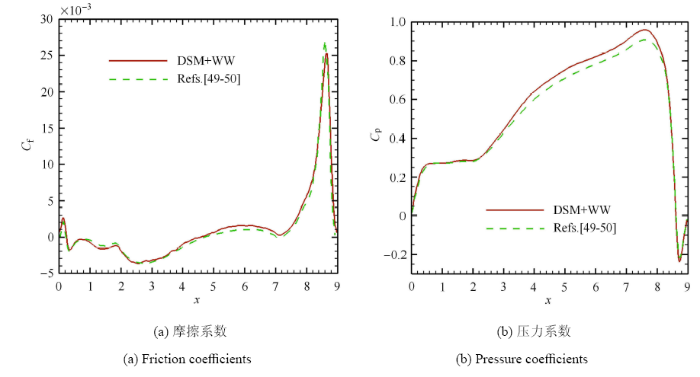
本文所得到的下壁面摩擦系数的结果与文献[49 ,50 ]的结果一致,如图11 (a)所示. 下壁面摩擦系数在流动分离点( x = 0.2 x = 4.6 x = 2.6 x = 8.6
图11 (b)比较了下壁面的压力系数 C p 49 ,50 ]的结果吻合较好,在流动恢复段有约 5 % 图11 (b)可以看出,压力系数在山顶后陡升,形成逆压梯度从而引起分离,接着压力系数在回流区的前半部分( x = 0.5 x = 2.0 x = 7.6 x = 8.7
图11 周期山状流下壁面摩擦系数与压力系数的比较
Fig. 11 The friction and the pressure coefficients along the bottom wall
3 结 论
本文根据湍流近壁流动的特征讨论了用于大涡模拟的壁模型,其中主要讨论了壁面应力模型. 壁面应力模型中已经被广泛研 究和使用的是平衡层模型,该类模型通过假定速度剖面(对数律或幂律)可以给出壁面切应力与近壁速度之间的联系. 但是如果近壁流动远离平衡状态,平衡层模型难以准确估计壁面切应力,此时需要考虑压力梯度等非平衡效应. 除了平衡层模型,双层模型也广泛用于求解壁面切应力,但是其应用过程比平衡层模型更复杂. 图3 画出了本文介绍的壁模型的关系图.
本文实现了基于WW模型的周期山状流的大涡模拟. 该大涡模拟基于非结构网格的有限体积方法来离散控制方程,并使用基于离散 动能守恒原理的方法,使用动态Smagorinsky模型作为亚格子模型,并且在不能解析壁面层的上壁面使用WW模型提供应力边界条件. 分析了流动的平均速度、脉动方差、雷诺应力、壁面压力以及摩擦力等统计量,本文的计算结果与文献的数值结果以及实验结果一致.
由于WW模型属于平衡层模型,而周期山状流下壁面附近存在流动分离、再附以及回流等压力梯度不能忽略的非平衡现象,因此 当前的工作在下壁面附近使用了能够解析壁面层的网格. 为了进一步减少计算量,可以在下壁面附近使用不能解析壁面层的网格,那就需要能够适用于分离流等复杂流动的壁模型,这是现在一个活跃的研究领域. 本文提到的考虑了压力梯度等非平衡效应的各种壁模型应该被广泛测试,以加深对这些模型适用范围的认识. 最后,当考虑湍流噪声问题, 需要精准计算壁面附近流动的时空关联,因此需要发展时间精准的壁模型[52 ] .
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
安翼 , 莫晃锐 , 刘青泉 . 高速列车头型长细比对气动噪声的影响
. 力学学报 , 2017 , 49 (5 ): 985 -996
[本文引用: 1]
(An Yi Mo Huangrui Liu Qingquan Study on the influence of the nose slenderness ratio of high-speed train on the aerodynamic noise
.Chinese Journal of Theoretical and Applied Mechanics , 2017 , 49 (5 ): 985 -996 (in Chinese))
[本文引用: 1]
[2]
林孟达 , 崔桂香 , 张兆顺 等 . 飞机尾涡演变及快速预测的大涡模拟研究
. 力学学报 , 2017 , 49 (6 ): 1185 -1200
[本文引用: 1]
(Lin Mengda Cui Guixiang Zhang Zhaoshun et al .Large eddy simulation on the evolution and the fast-time prediction of aircraft wake vortices
.Chinese Journal of Theoretical and Applied Mechanics , 2017 , 49 (6 ): 1185 -1200 (in Chinese))
[本文引用: 1]
[3]
冯峰 , 郭力 , 王强 . 高亚声速喷流气动噪声数值分析
. 力学学报 ,2016 , 48 (5 ): 1049 -1060
[本文引用: 1]
(Feng Feng Guo Li Wang Qiang Numerical investigation of noise of a high subsonic turbulent jet
.Chinese Journal of Theoretical and Applied Mechanics , 2016 , 48 (5 ): 1049 -1060 (in Chinese))
[本文引用: 1]
[4]
王纪 , 邱翔 , 罗剑平 等 . 湍流强度对预混燃烧影响的大涡模拟研究
. 力学季刊 , 2014 (4 ): 548 -559
[本文引用: 1]
(Wang Ji Qiu Xiang Luo Jianping et al .Large eddy simulation of the effects of turbulence intensity on premixed combustion
.Chinese Quarterly of Mechanics 2014 (4 ): 548 -559 (in Chinese))
[本文引用: 1]
[5]
刘难生 , 仲峰泉 , 陆夕云 等 . 旋转圆管湍流的大涡模拟数值研究
. 力学学报 , 2002 , 34 (6 ): 833 -846
[本文引用: 1]
(Liu Nansheng Zhong Fengquan Lu Xiyun et al .Large eddy simulation on turbulent flow in a pipe rotating about its axis
.Chinese Journal of Theoretical and Applied Mechanics , 2002 , 34 (6 ): 833 -846 (in Chinese))
[本文引用: 1]
[6]
Moin P Bodart J Bose S et al .Wall-modeling in complex turbulent flows
//Braza M, Bottaro A, Thompson M, eds. Advances in Fluid-Structure Interaction, Berlin: Springer , 2016 : 207 -19
[本文引用: 2]
[7]
Park GI Moin P Wall-modeled LES: Recent applications to complex flows//
Annual Research Briefs 2016. Stanford, CA: Cent. Turbul. Res. , 2016 : 39 -50
[本文引用: 1]
[8]
Choi H Moin P Grid-point requirements for large eddy simulation: Chapman’s estimates revisited
.Phys Fluids , 2012 , 24 (1 ): 011702
[本文引用: 1]
[9]
Piomelli U Balaras E Wall-layer models for large-eddy simulations
.Annu Rev Fluid Mech , 2002 , 34 (1 ): 349 -374
[本文引用: 6]
[10]
Piomelli U Wall-layer models for large-eddy simulation
.Progress in Aerospace Sciences , 2008 , 44 (6 ): 437 -446
[本文引用: 4]
[11]
Sagaut P Large Eddy Simulation for Incompressible Flows: An Introduction
. Berlin: Springer , 2006
[本文引用: 2]
[12]
许春晓 . 壁湍流相干结构和减阻控制机理
. 力学进展 , 2015 , 45 : 201504
[本文引用: 1]
(Xu Chunxiao Coherent structures and drag-reduction mechanism in wall turbulence
.Advances in Mechanics , 2015 , 45 : 201504 (in Chinese))
[本文引用: 1]
[13]
Chaouat B The state of the art of hybrid RANS/LES modeling for the simulation of turbulent flows
.Flow Turbul Combust , 2017 , 99 (2 ): 279 -327
[本文引用: 1]
[14]
Fu S Xiao ZX Chen HX et al .Simulation of wing-body junction flows with hybrid RANS/LES methods
.International Journal of Heat and Fluid Flow , 2007 , 28 (6 ): 1379 -1390
[本文引用: 1]
[15]
Balin R Spalart PR Jansen KE An investigation into the reduction of log-layer mismatch in wall-modeled LES with a hybrid RANS/LES approach
//Bulletin of the American Physical Society , 2017 , 62
[本文引用: 1]
[16]
Bose ST Park GI Wall-Modeled Large-eddy simulation for complex turbulent flows
.Annu Rev Fluid Mech , 2018 , 50 (1 ): 535 -561
[本文引用: 1]
[17]
Schumann U Subgrid scale model for finite difference simulations of turbulent flows in plane channels and annuli
.J Comput Phys , 1975 , 18 (4 ): 376 -404
[本文引用: 5]
[18]
Grötzbach G Direct numerical and large eddy simulation of turbulent channel flows
.Encyclopedia of fluid mechanics , 1987 , 6 : 1337 -1391
[本文引用: 1]
[19]
Werner H Wengle H Large-eddy simulation of turbulent flow over and around a cube in a plate channel//Werner H, Wengle H, eds. Turbulent Shear Flows 8
. Berlin: Springer , 1993 : 155 -168
[本文引用: 1]
[20]
Inagaki M Murata O Kondoh T et al .Numerical prediction of fluid-resonant oscillation at low mach number
.AIAA Journal , 2002 , 40 (9 ): 1823 -1829
[本文引用: 1]
[21]
Breuer M Rodi W Large eddy simulation of complexturbulent flows of practical interest//Hirschel EH, ed. Flow Simulation with High Performance Computers II
. Braunschweig: Vieweg , 1996 . 258 -274
[本文引用: 1]
[22]
Rajagopalan S Antonia RA Some properties of the large structure in a fully developed turbulent duct flow
. Phys Fluids , 1979 , 22 (4 ): 614 -622
[本文引用: 1]
[23]
Piomelli U Ferziger J Moin P et al .New approximate boundary conditions for large eddy simulations of wall-bounded flows
.Physics of Fluids A: Fluid Dynamics , 1989 , 1 (6 ): 1061 -1068
[本文引用: 1]
[24]
Skote M Henningson DS Direct numerical simulation of a separated turbulent boundary layer
.J Fluid Mech , 2002 , 471 : 107 -136
[本文引用: 1]
[25]
Larsson J Kawai S Bodart J et al .Large eddy simulation with modeled wall-stress: Recent progress and future directions
.Mech Eng Rev , 2016 , 3 (1 ): 15 -00418
[本文引用: 1]
[26]
Breuer M Kniazev B Abel M Development of wall models for LES of separated flows using statistical evaluations
.Computer & Fluids 2007 , 36 : 817 -837
[本文引用: 1]
[27]
Duprat C Balarac G Métais O et al .A wall-layer model for large-eddy simulations of turbulent flows with/out pressure gradient
.Phys. Fluids , 2011 , 23 (1 ): 015101
[本文引用: 2]
[28]
Yang X Sadique J Mittal R et al .Integral wall model for large eddy simulations of wall-bounded turbulent flows
.Phys Fluids , 2015 , 27 (2 ): 025112
[本文引用: 1]
[29]
Nicoud F Baggett JS Moin P et al .Large eddy simulation wall-modeling based on suboptimal control theory and linear stochastic estimation
.Phys. Fluids , 2001 , 13 (10 ): 2968 -2984
[本文引用: 2]
[30]
Bae HJ Lozano-Durán A Bose ST et al .Turbulence intensities in large-eddy simulation of wall-bounded flows
.Phys Rev Fluids , 2018 , 3 (1 ): 014610
[本文引用: 1]
[31]
Bae HJ Lozano-Durán A Moin P Investigation of the slip boundary condition in wall-modeled LES//Annual Research Briefs 2016
. Stanford, CA: Cent. Turbul. Res. 2016 : 75 -86
[本文引用: 1]
[32]
Yang X Bose ST Moin P A physics-based interpretation of the slip-wall LES model//Annual ResearchBriefs 2016
. Stanford, CA: Cent. Turbul. Res. 2016 : 65 -74
[本文引用: 1]
[33]
Lozano-Durán A Bae HJ Bose ST et al . Dynamic wall models for the slip boundary condition//Annual Research Briefs 2017
. Stanford, CA: Cent. Turbul. Res. 2017 . In press
[本文引用: 1]
[34]
Balaras E Benocci C Piomelli U Two-layer approximate boundary conditions for large-eddy simulations
.AIAA Journal , 1996 , 34 (6 ): 1111 -1119
[本文引用: 2]
[35]
Wang M Moin P Dynamic wall modeling for large-eddy simulation of complex turbulent flows
.Phys Fluids , 2002 , 14 (7 ): 2043 -2051
[本文引用: 2]
[36]
Kawai S Larsson J Dynamic non-equilibrium wall-modeling for large eddy simulation at high Reynolds numbers
.Phys Fluids , 2013 , 25 (1 ): 015105
[本文引用: 2]
[37]
Park GI Moin P An improved dynamic non-equilibrium wall-model for large eddy simulation
.Phys. Fluids , 2014 , 26 (1 ): 37 -48
[本文引用: 1]
[38]
Park GI Moin P Numerical aspects and implementation of a two-layer zonal wall model for LES ofcompressible turbulent flows on unstructured meshes
.J Comput Phys , 2016 , 305 : 589 -603
[本文引用: 1]
[39]
张兆顺 , 崔桂香 , 许春晓 . 湍流大涡数值模拟的理论与应用 . 北京 : 清华大学出版社 , 2008 : 194 -196
(Zhang Zhaoshun Cui Guixiang Xu Chunxiao. Theory and Application of Large-Eddy Simulation of Turbulent Flows. Beijing : Tsinghua University Press , 2008 : 194 -196 (in Chinese))
[40]
崔桂香 , 许春晓 , 张兆顺 . 湍流大涡数值模拟进展
. 空气动力学学报 , 2004 , 22 (2 ): 121 -129
[本文引用: 1]
(Cui Guixiang Xu Chunxiao Zhang Zhaoshun Progress in large eddy simulation of turbulent flows
.Acta Aerodynamica Sinica , 2004 , 22 (2 ): 121 -129 (in Chinese))
[本文引用: 1]
[41]
Tunstall R Laurence D Prosser R et al .Towards a generalised dual-mesh hybrid LES/RANS framework with improved consistency
.Computers & Fluids 2017 , 157 : 73 -83
[本文引用: 1]
[42]
Kumar G Lakshmanan SK Gopalan H et al .Investigation of the sensitivity of turbulent closures and coupling of hybrid RANS-LES models for predicting flow fields with separation and reattachment
.International Journal for Numerical Methods in Fluids , 2017 , 83 (12 ): 917 -939
[本文引用: 1]
[43]
Kadoch B Reimann T Schneider K et al .Comparison of a spectral method with volume penalization and a finite volume method with body fitted grids for turbulent flows
.Computers & Fluids 2016 , 133 : 140 -150
[本文引用: 1]
[44]
Wu JL Wang JX Xiao H et al .A priori assessment of prediction confidence for data-driven turbulence modeling
.Flow Turbul Combust , 2017 , 99 (1 ): 25 -46
[本文引用: 1]
[45]
Smagorinsky J General circulation experiments with the primitive equations
.Monthly Weather Review , 1963 , 91 (3 ): 99 -164
[本文引用: 1]
[46]
Germano M Piomelli U Moin P et al .A dynamic subgrid-scale eddy viscosity model
.Physics of Fluids A: Fluid Dynamics , 1991 , 3 (7 ): 1760 -1765
[本文引用: 1]
[47]
Lilly DK A proposed modification of the Germanosubgrid-scale closure method
.Physics of Fluids A: Fluid Dynamics , 1992 , 4 (3 ): 633 -635
[本文引用: 1]
[48]
You D Ham F Moin P Discrete conservation principles in large-eddy simulation with application to separation control over an airfoil
.Phys Fluids , 2008 , 20 (10 ): 101515
[本文引用: 1]
[49]
Temmerman L Leschziner MA Mellen CP et al .Investigation of wall-function approximations and subgrid-scale models in large eddy simulation of separated flow in a channel with streamwise periodic constrictions
.Int J Heat Fluid Flow , 2003 , 24 (2 ): 157 -180
[本文引用: 8]
[50]
Fröhlich J Mellen CP Rodi W et al .Highly resolved large-eddy simulation of separated flow in a channel with streamwise periodic constrictions
.J Fluid Mech , 2005 , 526 : 19 -66
[本文引用: 8]
[51]
Breuer M Peller N Rapp C et al .Flow over periodic hills-numerical and experimental study in a wide range of Reynolds numbers
.Computers & Fluids 2009 , 38 (2 ): 433 -457
[本文引用: 3]
[52]
He GW Jin GD Yang Y Space-time correlations and dynamic coupling in turbulent flows
.Annu Rev Fluid Mech , 2017 , 49 : 51 -70
[本文引用: 1]
高速列车头型长细比对气动噪声的影响
1
2017
... 大涡模拟 是模拟和预测非定常湍流的有效工具,它的基本思想是数值求解大涡的运动,而采用物理模型模拟小涡对大涡的影响. 比较而言,直接数值模拟 虽然可以模拟非定常湍流,但其巨大的计算量导致难以用于工程实际. 雷诺平均 方法的计算量较小,因此常用于工程问题[1 ] ,但它难以用于预测大涡运动的非定常特性. 随着计算机的发展,大涡模拟已经越来越多地被应用于科学研究和工程设计[2 ,3 ,4 ,5 ] . 当大涡模拟用于壁湍流时,由于壁面会引入正比于壁面距离的新的尺度,因此在壁面附近,大涡模拟又分为解析壁面 层(wall-resolved)的大涡模拟和模化壁面层(wall-modeled)的大涡模拟[6 ,7 ] . 解析壁面层的网格尺度与黏性长度同量级,模化壁面层的网格尺度与边界层厚度同量级,因此模化壁面层的大涡模拟所需的网 格量远小于解析壁面层的网格量. 例如,在一个计算机翼绕流的算例中,当雷诺数 Re = 1 0 9 [8 ] 因此,模化壁面层的大涡模拟在工程中有重要意义. ...
高速列车头型长细比对气动噪声的影响
1
2017
... 大涡模拟 是模拟和预测非定常湍流的有效工具,它的基本思想是数值求解大涡的运动,而采用物理模型模拟小涡对大涡的影响. 比较而言,直接数值模拟 虽然可以模拟非定常湍流,但其巨大的计算量导致难以用于工程实际. 雷诺平均 方法的计算量较小,因此常用于工程问题[1 ] ,但它难以用于预测大涡运动的非定常特性. 随着计算机的发展,大涡模拟已经越来越多地被应用于科学研究和工程设计[2 ,3 ,4 ,5 ] . 当大涡模拟用于壁湍流时,由于壁面会引入正比于壁面距离的新的尺度,因此在壁面附近,大涡模拟又分为解析壁面 层(wall-resolved)的大涡模拟和模化壁面层(wall-modeled)的大涡模拟[6 ,7 ] . 解析壁面层的网格尺度与黏性长度同量级,模化壁面层的网格尺度与边界层厚度同量级,因此模化壁面层的大涡模拟所需的网 格量远小于解析壁面层的网格量. 例如,在一个计算机翼绕流的算例中,当雷诺数 Re = 1 0 9 [8 ] 因此,模化壁面层的大涡模拟在工程中有重要意义. ...
飞机尾涡演变及快速预测的大涡模拟研究
1
2017
... 大涡模拟 是模拟和预测非定常湍流的有效工具,它的基本思想是数值求解大涡的运动,而采用物理模型模拟小涡对大涡的影响. 比较而言,直接数值模拟 虽然可以模拟非定常湍流,但其巨大的计算量导致难以用于工程实际. 雷诺平均 方法的计算量较小,因此常用于工程问题[1 ] ,但它难以用于预测大涡运动的非定常特性. 随着计算机的发展,大涡模拟已经越来越多地被应用于科学研究和工程设计[2 ,3 ,4 ,5 ] . 当大涡模拟用于壁湍流时,由于壁面会引入正比于壁面距离的新的尺度,因此在壁面附近,大涡模拟又分为解析壁面 层(wall-resolved)的大涡模拟和模化壁面层(wall-modeled)的大涡模拟[6 ,7 ] . 解析壁面层的网格尺度与黏性长度同量级,模化壁面层的网格尺度与边界层厚度同量级,因此模化壁面层的大涡模拟所需的网 格量远小于解析壁面层的网格量. 例如,在一个计算机翼绕流的算例中,当雷诺数 Re = 1 0 9 [8 ] 因此,模化壁面层的大涡模拟在工程中有重要意义. ...
飞机尾涡演变及快速预测的大涡模拟研究
1
2017
... 大涡模拟 是模拟和预测非定常湍流的有效工具,它的基本思想是数值求解大涡的运动,而采用物理模型模拟小涡对大涡的影响. 比较而言,直接数值模拟 虽然可以模拟非定常湍流,但其巨大的计算量导致难以用于工程实际. 雷诺平均 方法的计算量较小,因此常用于工程问题[1 ] ,但它难以用于预测大涡运动的非定常特性. 随着计算机的发展,大涡模拟已经越来越多地被应用于科学研究和工程设计[2 ,3 ,4 ,5 ] . 当大涡模拟用于壁湍流时,由于壁面会引入正比于壁面距离的新的尺度,因此在壁面附近,大涡模拟又分为解析壁面 层(wall-resolved)的大涡模拟和模化壁面层(wall-modeled)的大涡模拟[6 ,7 ] . 解析壁面层的网格尺度与黏性长度同量级,模化壁面层的网格尺度与边界层厚度同量级,因此模化壁面层的大涡模拟所需的网 格量远小于解析壁面层的网格量. 例如,在一个计算机翼绕流的算例中,当雷诺数 Re = 1 0 9 [8 ] 因此,模化壁面层的大涡模拟在工程中有重要意义. ...
高亚声速喷流气动噪声数值分析
1
2016
... 大涡模拟 是模拟和预测非定常湍流的有效工具,它的基本思想是数值求解大涡的运动,而采用物理模型模拟小涡对大涡的影响. 比较而言,直接数值模拟 虽然可以模拟非定常湍流,但其巨大的计算量导致难以用于工程实际. 雷诺平均 方法的计算量较小,因此常用于工程问题[1 ] ,但它难以用于预测大涡运动的非定常特性. 随着计算机的发展,大涡模拟已经越来越多地被应用于科学研究和工程设计[2 ,3 ,4 ,5 ] . 当大涡模拟用于壁湍流时,由于壁面会引入正比于壁面距离的新的尺度,因此在壁面附近,大涡模拟又分为解析壁面 层(wall-resolved)的大涡模拟和模化壁面层(wall-modeled)的大涡模拟[6 ,7 ] . 解析壁面层的网格尺度与黏性长度同量级,模化壁面层的网格尺度与边界层厚度同量级,因此模化壁面层的大涡模拟所需的网 格量远小于解析壁面层的网格量. 例如,在一个计算机翼绕流的算例中,当雷诺数 Re = 1 0 9 [8 ] 因此,模化壁面层的大涡模拟在工程中有重要意义. ...
高亚声速喷流气动噪声数值分析
1
2016
... 大涡模拟 是模拟和预测非定常湍流的有效工具,它的基本思想是数值求解大涡的运动,而采用物理模型模拟小涡对大涡的影响. 比较而言,直接数值模拟 虽然可以模拟非定常湍流,但其巨大的计算量导致难以用于工程实际. 雷诺平均 方法的计算量较小,因此常用于工程问题[1 ] ,但它难以用于预测大涡运动的非定常特性. 随着计算机的发展,大涡模拟已经越来越多地被应用于科学研究和工程设计[2 ,3 ,4 ,5 ] . 当大涡模拟用于壁湍流时,由于壁面会引入正比于壁面距离的新的尺度,因此在壁面附近,大涡模拟又分为解析壁面 层(wall-resolved)的大涡模拟和模化壁面层(wall-modeled)的大涡模拟[6 ,7 ] . 解析壁面层的网格尺度与黏性长度同量级,模化壁面层的网格尺度与边界层厚度同量级,因此模化壁面层的大涡模拟所需的网 格量远小于解析壁面层的网格量. 例如,在一个计算机翼绕流的算例中,当雷诺数 Re = 1 0 9 [8 ] 因此,模化壁面层的大涡模拟在工程中有重要意义. ...
湍流强度对预混燃烧影响的大涡模拟研究
1
2014
... 大涡模拟 是模拟和预测非定常湍流的有效工具,它的基本思想是数值求解大涡的运动,而采用物理模型模拟小涡对大涡的影响. 比较而言,直接数值模拟 虽然可以模拟非定常湍流,但其巨大的计算量导致难以用于工程实际. 雷诺平均 方法的计算量较小,因此常用于工程问题[1 ] ,但它难以用于预测大涡运动的非定常特性. 随着计算机的发展,大涡模拟已经越来越多地被应用于科学研究和工程设计[2 ,3 ,4 ,5 ] . 当大涡模拟用于壁湍流时,由于壁面会引入正比于壁面距离的新的尺度,因此在壁面附近,大涡模拟又分为解析壁面 层(wall-resolved)的大涡模拟和模化壁面层(wall-modeled)的大涡模拟[6 ,7 ] . 解析壁面层的网格尺度与黏性长度同量级,模化壁面层的网格尺度与边界层厚度同量级,因此模化壁面层的大涡模拟所需的网 格量远小于解析壁面层的网格量. 例如,在一个计算机翼绕流的算例中,当雷诺数 Re = 1 0 9 [8 ] 因此,模化壁面层的大涡模拟在工程中有重要意义. ...
湍流强度对预混燃烧影响的大涡模拟研究
1
2014
... 大涡模拟 是模拟和预测非定常湍流的有效工具,它的基本思想是数值求解大涡的运动,而采用物理模型模拟小涡对大涡的影响. 比较而言,直接数值模拟 虽然可以模拟非定常湍流,但其巨大的计算量导致难以用于工程实际. 雷诺平均 方法的计算量较小,因此常用于工程问题[1 ] ,但它难以用于预测大涡运动的非定常特性. 随着计算机的发展,大涡模拟已经越来越多地被应用于科学研究和工程设计[2 ,3 ,4 ,5 ] . 当大涡模拟用于壁湍流时,由于壁面会引入正比于壁面距离的新的尺度,因此在壁面附近,大涡模拟又分为解析壁面 层(wall-resolved)的大涡模拟和模化壁面层(wall-modeled)的大涡模拟[6 ,7 ] . 解析壁面层的网格尺度与黏性长度同量级,模化壁面层的网格尺度与边界层厚度同量级,因此模化壁面层的大涡模拟所需的网 格量远小于解析壁面层的网格量. 例如,在一个计算机翼绕流的算例中,当雷诺数 Re = 1 0 9 [8 ] 因此,模化壁面层的大涡模拟在工程中有重要意义. ...
旋转圆管湍流的大涡模拟数值研究
1
2002
... 大涡模拟 是模拟和预测非定常湍流的有效工具,它的基本思想是数值求解大涡的运动,而采用物理模型模拟小涡对大涡的影响. 比较而言,直接数值模拟 虽然可以模拟非定常湍流,但其巨大的计算量导致难以用于工程实际. 雷诺平均 方法的计算量较小,因此常用于工程问题[1 ] ,但它难以用于预测大涡运动的非定常特性. 随着计算机的发展,大涡模拟已经越来越多地被应用于科学研究和工程设计[2 ,3 ,4 ,5 ] . 当大涡模拟用于壁湍流时,由于壁面会引入正比于壁面距离的新的尺度,因此在壁面附近,大涡模拟又分为解析壁面 层(wall-resolved)的大涡模拟和模化壁面层(wall-modeled)的大涡模拟[6 ,7 ] . 解析壁面层的网格尺度与黏性长度同量级,模化壁面层的网格尺度与边界层厚度同量级,因此模化壁面层的大涡模拟所需的网 格量远小于解析壁面层的网格量. 例如,在一个计算机翼绕流的算例中,当雷诺数 Re = 1 0 9 [8 ] 因此,模化壁面层的大涡模拟在工程中有重要意义. ...
旋转圆管湍流的大涡模拟数值研究
1
2002
... 大涡模拟 是模拟和预测非定常湍流的有效工具,它的基本思想是数值求解大涡的运动,而采用物理模型模拟小涡对大涡的影响. 比较而言,直接数值模拟 虽然可以模拟非定常湍流,但其巨大的计算量导致难以用于工程实际. 雷诺平均 方法的计算量较小,因此常用于工程问题[1 ] ,但它难以用于预测大涡运动的非定常特性. 随着计算机的发展,大涡模拟已经越来越多地被应用于科学研究和工程设计[2 ,3 ,4 ,5 ] . 当大涡模拟用于壁湍流时,由于壁面会引入正比于壁面距离的新的尺度,因此在壁面附近,大涡模拟又分为解析壁面 层(wall-resolved)的大涡模拟和模化壁面层(wall-modeled)的大涡模拟[6 ,7 ] . 解析壁面层的网格尺度与黏性长度同量级,模化壁面层的网格尺度与边界层厚度同量级,因此模化壁面层的大涡模拟所需的网 格量远小于解析壁面层的网格量. 例如,在一个计算机翼绕流的算例中,当雷诺数 Re = 1 0 9 [8 ] 因此,模化壁面层的大涡模拟在工程中有重要意义. ...
Wall-modeling in complex turbulent flows
2
2016
... 大涡模拟 是模拟和预测非定常湍流的有效工具,它的基本思想是数值求解大涡的运动,而采用物理模型模拟小涡对大涡的影响. 比较而言,直接数值模拟 虽然可以模拟非定常湍流,但其巨大的计算量导致难以用于工程实际. 雷诺平均 方法的计算量较小,因此常用于工程问题[1 ] ,但它难以用于预测大涡运动的非定常特性. 随着计算机的发展,大涡模拟已经越来越多地被应用于科学研究和工程设计[2 ,3 ,4 ,5 ] . 当大涡模拟用于壁湍流时,由于壁面会引入正比于壁面距离的新的尺度,因此在壁面附近,大涡模拟又分为解析壁面 层(wall-resolved)的大涡模拟和模化壁面层(wall-modeled)的大涡模拟[6 ,7 ] . 解析壁面层的网格尺度与黏性长度同量级,模化壁面层的网格尺度与边界层厚度同量级,因此模化壁面层的大涡模拟所需的网 格量远小于解析壁面层的网格量. 例如,在一个计算机翼绕流的算例中,当雷诺数 Re = 1 0 9 [8 ] 因此,模化壁面层的大涡模拟在工程中有重要意义. ...
... Schumann[17 ] 提出了一种根据壁面律计算壁面切应力的模型(常被称为平衡层模型[6 ] ),该模型从已解析的流场中构造瞬时壁面应力边界条件 ...
Wall-modeled LES: Recent applications to complex flows//
1
2016
... 大涡模拟 是模拟和预测非定常湍流的有效工具,它的基本思想是数值求解大涡的运动,而采用物理模型模拟小涡对大涡的影响. 比较而言,直接数值模拟 虽然可以模拟非定常湍流,但其巨大的计算量导致难以用于工程实际. 雷诺平均 方法的计算量较小,因此常用于工程问题[1 ] ,但它难以用于预测大涡运动的非定常特性. 随着计算机的发展,大涡模拟已经越来越多地被应用于科学研究和工程设计[2 ,3 ,4 ,5 ] . 当大涡模拟用于壁湍流时,由于壁面会引入正比于壁面距离的新的尺度,因此在壁面附近,大涡模拟又分为解析壁面 层(wall-resolved)的大涡模拟和模化壁面层(wall-modeled)的大涡模拟[6 ,7 ] . 解析壁面层的网格尺度与黏性长度同量级,模化壁面层的网格尺度与边界层厚度同量级,因此模化壁面层的大涡模拟所需的网 格量远小于解析壁面层的网格量. 例如,在一个计算机翼绕流的算例中,当雷诺数 Re = 1 0 9 [8 ] 因此,模化壁面层的大涡模拟在工程中有重要意义. ...
Grid-point requirements for large eddy simulation: Chapman’s estimates revisited
1
2012
... 大涡模拟 是模拟和预测非定常湍流的有效工具,它的基本思想是数值求解大涡的运动,而采用物理模型模拟小涡对大涡的影响. 比较而言,直接数值模拟 虽然可以模拟非定常湍流,但其巨大的计算量导致难以用于工程实际. 雷诺平均 方法的计算量较小,因此常用于工程问题[1 ] ,但它难以用于预测大涡运动的非定常特性. 随着计算机的发展,大涡模拟已经越来越多地被应用于科学研究和工程设计[2 ,3 ,4 ,5 ] . 当大涡模拟用于壁湍流时,由于壁面会引入正比于壁面距离的新的尺度,因此在壁面附近,大涡模拟又分为解析壁面 层(wall-resolved)的大涡模拟和模化壁面层(wall-modeled)的大涡模拟[6 ,7 ] . 解析壁面层的网格尺度与黏性长度同量级,模化壁面层的网格尺度与边界层厚度同量级,因此模化壁面层的大涡模拟所需的网 格量远小于解析壁面层的网格量. 例如,在一个计算机翼绕流的算例中,当雷诺数 Re = 1 0 9 [8 ] 因此,模化壁面层的大涡模拟在工程中有重要意义. ...
Wall-layer models for large-eddy simulations
6
2002
... 壁面附近湍流结构的特征尺度正比于其与壁面间的距离. 如果完全解析近壁湍流结构,大涡模拟所需的计算量与直接数值模拟相当. 解析壁面层的大涡模拟大部分的网格用于解析近壁流动. Re > 1 0 6 [9 ,10 ] . 壁面附近的流动常满足特定的规律并趋于形成自维持过程[11 ,12 ] . 近壁湍流的上述特性使得可以采用简化的方法或模型刻画近壁流动,常用的简化方案有雷诺平均与大涡模拟混合方法[13 ,14 ,15 ] 和壁模型[9 -10 ,16 ] . 本文介绍采用壁模型简化近壁流动的方案. ...
... [9 -10 ,16 ]. 本文介绍采用壁模型简化近壁流动的方案. ...
... 湍流大涡模拟区域与壁模型示意图. 边界附近的网格不足以解析近壁流动结构时,常用的有限差分算子得到的黏性应力项并不 是壁面切应力的正确值. 壁模型可以在较粗的网格上保证近壁的动量守恒,从而得到正确的速度分布(根据Piomelli和Balaras[9 ] 的图2 修改而来) ...
... 上述壁面应力模型均由近壁的瞬时速度确定壁面应力. 这一做法的物理基础是对数律区的速度与壁面应力相关的实验现象[22 ] . 这一物理基础隐含了上述模型中所用到的已解析的近壁流场速度位于对数律区,即:距壁面的第一层网格不超过对数律区. 值得注意的是,这种基于统计平均的速度分布又要求近壁流动的网格要适当的粗,以保证单位网格区域内包含足够数量的小尺度结构[9 ] . 实际计算中常取距壁面的第一层网格位于对数律区或黏性子区的上层. 上述壁面应力模型没有考虑边界层内的相干结构对壁面应力和速度脉动的影响,而边界层内的倾斜结构以及下扫和喷射过程都会影响壁面应力和速度脉动的关联. Piomelli等[23 ] 通过引入流向距离参数考虑倾斜结构引起的壁面切应力与近壁速度之间的滞后现象. ...
... 壁面应力模型的基础是近壁平均速度分布的壁面律,但普适的壁面律在具有逆压梯度的流动中并不存在[24 ] . 尽管如此,这些模型仍被广泛地应用于建筑物绕流、风场以及大气边界层等高雷诺数复杂壁湍流的大涡模拟[9 ,10 ] ,并且常可得到合理的结果,尤其是流动的平均量. Larsson等[25 ] 对这一现象的解释为:(1)壁面应力模型仅模化了边界层内区的部分流动(约占边界层厚度的20%),大涡模拟可以解析80%边界层厚度内的非平衡效应;并且未解析的20%近壁流动的时间尺度远小于已解析的流动尺度(因流动的时间尺度与壁面距离成正比);(2)逆压梯度较大的流动区域往往对应于对流项较大的区域,两者对壁面应力的影响可相互抵消. 但同时,也有工作表明平衡律模型难以准确计算分离流动的壁面摩擦力[10 ] . ...
... 由上可以看到,双层模型比基于壁面律的壁面应力模型更易考虑非平衡效应,但其应用过程也相应 比较复杂. 与双层模型相 关的综述或介绍可参见文献[9 ,38 -40 ] . ...
Wall-layer models for large-eddy simulation
4
2008
... 壁面附近湍流结构的特征尺度正比于其与壁面间的距离. 如果完全解析近壁湍流结构,大涡模拟所需的计算量与直接数值模拟相当. 解析壁面层的大涡模拟大部分的网格用于解析近壁流动. Re > 1 0 6 [9 ,10 ] . 壁面附近的流动常满足特定的规律并趋于形成自维持过程[11 ,12 ] . 近壁湍流的上述特性使得可以采用简化的方法或模型刻画近壁流动,常用的简化方案有雷诺平均与大涡模拟混合方法[13 ,14 ,15 ] 和壁模型[9 -10 ,16 ] . 本文介绍采用壁模型简化近壁流动的方案. ...
... -10 ,16 ]. 本文介绍采用壁模型简化近壁流动的方案. ...
... 壁面应力模型的基础是近壁平均速度分布的壁面律,但普适的壁面律在具有逆压梯度的流动中并不存在[24 ] . 尽管如此,这些模型仍被广泛地应用于建筑物绕流、风场以及大气边界层等高雷诺数复杂壁湍流的大涡模拟[9 ,10 ] ,并且常可得到合理的结果,尤其是流动的平均量. Larsson等[25 ] 对这一现象的解释为:(1)壁面应力模型仅模化了边界层内区的部分流动(约占边界层厚度的20%),大涡模拟可以解析80%边界层厚度内的非平衡效应;并且未解析的20%近壁流动的时间尺度远小于已解析的流动尺度(因流动的时间尺度与壁面距离成正比);(2)逆压梯度较大的流动区域往往对应于对流项较大的区域,两者对壁面应力的影响可相互抵消. 但同时,也有工作表明平衡律模型难以准确计算分离流动的壁面摩擦力[10 ] . ...
... [10 ]. ...
Large Eddy Simulation for Incompressible Flows: An Introduction
2
2006
... 壁面附近湍流结构的特征尺度正比于其与壁面间的距离. 如果完全解析近壁湍流结构,大涡模拟所需的计算量与直接数值模拟相当. 解析壁面层的大涡模拟大部分的网格用于解析近壁流动. Re > 1 0 6 [9 ,10 ] . 壁面附近的流动常满足特定的规律并趋于形成自维持过程[11 ,12 ] . 近壁湍流的上述特性使得可以采用简化的方法或模型刻画近壁流动,常用的简化方案有雷诺平均与大涡模拟混合方法[13 ,14 ,15 ] 和壁模型[9 -10 ,16 ] . 本文介绍采用壁模型简化近壁流动的方案. ...
... Sagaut[11 ] 将大涡模拟壁模型分为4类:高阶边界条件(high-order boundary conditions),壁面应力模型(wall-stress models),离面边界条件(off-wall boundary conditions) 和确定性最小边界层单元模拟(deterministic minimal boundary-layer unit simulation),其中壁面应力模型的应用最为广泛. ...
壁湍流相干结构和减阻控制机理
1
2015
... 壁面附近湍流结构的特征尺度正比于其与壁面间的距离. 如果完全解析近壁湍流结构,大涡模拟所需的计算量与直接数值模拟相当. 解析壁面层的大涡模拟大部分的网格用于解析近壁流动. Re > 1 0 6 [9 ,10 ] . 壁面附近的流动常满足特定的规律并趋于形成自维持过程[11 ,12 ] . 近壁湍流的上述特性使得可以采用简化的方法或模型刻画近壁流动,常用的简化方案有雷诺平均与大涡模拟混合方法[13 ,14 ,15 ] 和壁模型[9 -10 ,16 ] . 本文介绍采用壁模型简化近壁流动的方案. ...
壁湍流相干结构和减阻控制机理
1
2015
... 壁面附近湍流结构的特征尺度正比于其与壁面间的距离. 如果完全解析近壁湍流结构,大涡模拟所需的计算量与直接数值模拟相当. 解析壁面层的大涡模拟大部分的网格用于解析近壁流动. Re > 1 0 6 [9 ,10 ] . 壁面附近的流动常满足特定的规律并趋于形成自维持过程[11 ,12 ] . 近壁湍流的上述特性使得可以采用简化的方法或模型刻画近壁流动,常用的简化方案有雷诺平均与大涡模拟混合方法[13 ,14 ,15 ] 和壁模型[9 -10 ,16 ] . 本文介绍采用壁模型简化近壁流动的方案. ...
The state of the art of hybrid RANS/LES modeling for the simulation of turbulent flows
1
2017
... 壁面附近湍流结构的特征尺度正比于其与壁面间的距离. 如果完全解析近壁湍流结构,大涡模拟所需的计算量与直接数值模拟相当. 解析壁面层的大涡模拟大部分的网格用于解析近壁流动. Re > 1 0 6 [9 ,10 ] . 壁面附近的流动常满足特定的规律并趋于形成自维持过程[11 ,12 ] . 近壁湍流的上述特性使得可以采用简化的方法或模型刻画近壁流动,常用的简化方案有雷诺平均与大涡模拟混合方法[13 ,14 ,15 ] 和壁模型[9 -10 ,16 ] . 本文介绍采用壁模型简化近壁流动的方案. ...
Simulation of wing-body junction flows with hybrid RANS/LES methods
1
2007
... 壁面附近湍流结构的特征尺度正比于其与壁面间的距离. 如果完全解析近壁湍流结构,大涡模拟所需的计算量与直接数值模拟相当. 解析壁面层的大涡模拟大部分的网格用于解析近壁流动. Re > 1 0 6 [9 ,10 ] . 壁面附近的流动常满足特定的规律并趋于形成自维持过程[11 ,12 ] . 近壁湍流的上述特性使得可以采用简化的方法或模型刻画近壁流动,常用的简化方案有雷诺平均与大涡模拟混合方法[13 ,14 ,15 ] 和壁模型[9 -10 ,16 ] . 本文介绍采用壁模型简化近壁流动的方案. ...
An investigation into the reduction of log-layer mismatch in wall-modeled LES with a hybrid RANS/LES approach
1
2017
... 壁面附近湍流结构的特征尺度正比于其与壁面间的距离. 如果完全解析近壁湍流结构,大涡模拟所需的计算量与直接数值模拟相当. 解析壁面层的大涡模拟大部分的网格用于解析近壁流动. Re > 1 0 6 [9 ,10 ] . 壁面附近的流动常满足特定的规律并趋于形成自维持过程[11 ,12 ] . 近壁湍流的上述特性使得可以采用简化的方法或模型刻画近壁流动,常用的简化方案有雷诺平均与大涡模拟混合方法[13 ,14 ,15 ] 和壁模型[9 -10 ,16 ] . 本文介绍采用壁模型简化近壁流动的方案. ...
Wall-Modeled Large-eddy simulation for complex turbulent flows
1
2018
... 壁面附近湍流结构的特征尺度正比于其与壁面间的距离. 如果完全解析近壁湍流结构,大涡模拟所需的计算量与直接数值模拟相当. 解析壁面层的大涡模拟大部分的网格用于解析近壁流动. Re > 1 0 6 [9 ,10 ] . 壁面附近的流动常满足特定的规律并趋于形成自维持过程[11 ,12 ] . 近壁湍流的上述特性使得可以采用简化的方法或模型刻画近壁流动,常用的简化方案有雷诺平均与大涡模拟混合方法[13 ,14 ,15 ] 和壁模型[9 -10 ,16 ] . 本文介绍采用壁模型简化近壁流动的方案. ...
Subgrid scale model for finite difference simulations of turbulent flows in plane channels and annuli
5
1975
... 为不失一般性, 以Schumann[17 ] 提供的方法为例在图2 所示的网格上离散动量方程(3) ...
... Schumann[17 ] 提出了一种根据壁面律计算壁面切应力的模型(常被称为平衡层模型[6 ] ),该模型从已解析的流场中构造瞬时壁面应力边界条件 ...
... 其中, u 1 u 1 τ w [17 ] 利用恒定压力梯度槽道和管道流动的特点给出平均壁面应力 τ w [17 ] 所给出的壁面应力模型的一个主要缺点是需要事先知道平均壁面应力. 克服这一缺点的一种方案是通过近壁的速度分布反推壁面切应力[18 ] ,即求解如下方程 ...
... [17 ]所给出的壁面应力模型的一个主要缺点是需要事先知道平均壁面应力. 克服这一缺点的一种方案是通过近壁的速度分布反推壁面切应力[18 ] ,即求解如下方程 ...
... 由此,根据WW模型得到了壁面切应力与近壁速度间的解析关系. 根据Schumann[17 ] 的假设,近壁附近的瞬时切向速度 和壁面切应力同向. 由此在计算中,上述表达式中壁面切应力 τ w U p
Direct numerical and large eddy simulation of turbulent channel flows
1
1987
... 其中, u 1 u 1 τ w [17 ] 利用恒定压力梯度槽道和管道流动的特点给出平均壁面应力 τ w [17 ] 所给出的壁面应力模型的一个主要缺点是需要事先知道平均壁面应力. 克服这一缺点的一种方案是通过近壁的速度分布反推壁面切应力[18 ] ,即求解如下方程 ...
Large-eddy simulation of turbulent flow over and around a cube in a plate channel//Werner H, Wengle H, eds. Turbulent Shear Flows 8
1
1993
... Werner-Wengle模型[19 ] (简称WW模型)采用瞬时速度代替平均速度,并采用线性律与幂律的匹配形式近似表示壁面速度分布,得到了壁面切应力与已解析的近壁流场速度的解析表达式. 与方程(7)相比,WW模型有两个优点:第一,可以通过瞬时速度求得瞬时壁面切应力;第二,避免了求解含有对数函数的超越方程. WW模型的速度剖面为 ...
Numerical prediction of fluid-resonant oscillation at low mach number
1
2002
... Inagaki等[20 ] 在WW模型的双层速度形式基础上引入了缓冲层的影响并通过修正后的三层速度匹配形式改进了计算结果 ...
Large eddy simulation of complexturbulent flows of practical interest//Hirschel EH, ed. Flow Simulation with High Performance Computers II
1
1996
... Breuer和Rodi[21 ] 在对数律中提出三层速度匹配形式,分段表示出线性律、缓冲层和对数律的速度剖面 ...
Some properties of the large structure in a fully developed turbulent duct flow
1
1979
... 上述壁面应力模型均由近壁的瞬时速度确定壁面应力. 这一做法的物理基础是对数律区的速度与壁面应力相关的实验现象[22 ] . 这一物理基础隐含了上述模型中所用到的已解析的近壁流场速度位于对数律区,即:距壁面的第一层网格不超过对数律区. 值得注意的是,这种基于统计平均的速度分布又要求近壁流动的网格要适当的粗,以保证单位网格区域内包含足够数量的小尺度结构[9 ] . 实际计算中常取距壁面的第一层网格位于对数律区或黏性子区的上层. 上述壁面应力模型没有考虑边界层内的相干结构对壁面应力和速度脉动的影响,而边界层内的倾斜结构以及下扫和喷射过程都会影响壁面应力和速度脉动的关联. Piomelli等[23 ] 通过引入流向距离参数考虑倾斜结构引起的壁面切应力与近壁速度之间的滞后现象. ...
New approximate boundary conditions for large eddy simulations of wall-bounded flows
1
1989
... 上述壁面应力模型均由近壁的瞬时速度确定壁面应力. 这一做法的物理基础是对数律区的速度与壁面应力相关的实验现象[22 ] . 这一物理基础隐含了上述模型中所用到的已解析的近壁流场速度位于对数律区,即:距壁面的第一层网格不超过对数律区. 值得注意的是,这种基于统计平均的速度分布又要求近壁流动的网格要适当的粗,以保证单位网格区域内包含足够数量的小尺度结构[9 ] . 实际计算中常取距壁面的第一层网格位于对数律区或黏性子区的上层. 上述壁面应力模型没有考虑边界层内的相干结构对壁面应力和速度脉动的影响,而边界层内的倾斜结构以及下扫和喷射过程都会影响壁面应力和速度脉动的关联. Piomelli等[23 ] 通过引入流向距离参数考虑倾斜结构引起的壁面切应力与近壁速度之间的滞后现象. ...
Direct numerical simulation of a separated turbulent boundary layer
1
2002
... 壁面应力模型的基础是近壁平均速度分布的壁面律,但普适的壁面律在具有逆压梯度的流动中并不存在[24 ] . 尽管如此,这些模型仍被广泛地应用于建筑物绕流、风场以及大气边界层等高雷诺数复杂壁湍流的大涡模拟[9 ,10 ] ,并且常可得到合理的结果,尤其是流动的平均量. Larsson等[25 ] 对这一现象的解释为:(1)壁面应力模型仅模化了边界层内区的部分流动(约占边界层厚度的20%),大涡模拟可以解析80%边界层厚度内的非平衡效应;并且未解析的20%近壁流动的时间尺度远小于已解析的流动尺度(因流动的时间尺度与壁面距离成正比);(2)逆压梯度较大的流动区域往往对应于对流项较大的区域,两者对壁面应力的影响可相互抵消. 但同时,也有工作表明平衡律模型难以准确计算分离流动的壁面摩擦力[10 ] . ...
Large eddy simulation with modeled wall-stress: Recent progress and future directions
1
2016
... 壁面应力模型的基础是近壁平均速度分布的壁面律,但普适的壁面律在具有逆压梯度的流动中并不存在[24 ] . 尽管如此,这些模型仍被广泛地应用于建筑物绕流、风场以及大气边界层等高雷诺数复杂壁湍流的大涡模拟[9 ,10 ] ,并且常可得到合理的结果,尤其是流动的平均量. Larsson等[25 ] 对这一现象的解释为:(1)壁面应力模型仅模化了边界层内区的部分流动(约占边界层厚度的20%),大涡模拟可以解析80%边界层厚度内的非平衡效应;并且未解析的20%近壁流动的时间尺度远小于已解析的流动尺度(因流动的时间尺度与壁面距离成正比);(2)逆压梯度较大的流动区域往往对应于对流项较大的区域,两者对壁面应力的影响可相互抵消. 但同时,也有工作表明平衡律模型难以准确计算分离流动的壁面摩擦力[10 ] . ...
Development of wall models for LES of separated flows using statistical evaluations
1
2007
... Breuer等[26 ] 从边界层方程出发,考虑了压力梯度的非平衡效应,对WW模型进行了推广. 该方法通过WW模型的幂律速度剖 面构造人工黏性,并通过统计估计定义黏性子层的相对厚度,在周期山状流的数值模拟中准确计算了流动的分离与壁面摩擦力. Duprat等[27 ] 在近壁流动的控制方程中直接考虑了流向压力梯度的非平衡效应,同时以流向压力梯度和壁面摩擦力为特征量, 引入近壁流动的混合特征速度,并以此对壁面单位进行了重新标度. 进一步地,Duprat等[27 ] 依据此混合速度提出了一种近壁涡黏系数衰减的新形式,从而引入了压力梯度对速度剖面和壁面应力 的影响. 相比于仅考虑平衡效应的壁面模型,定义混合速度有效地克服了流动分离点附近的奇异性,并有效地反映了流向压力梯度对流动的影响. 该壁模型准确模拟了周期山状流,尤其在流动的逆压区取得较好的预测结果,数值结果表明在非平衡壁模型中同时考虑了压力梯度和雷诺应力具有重要意义. ...
A wall-layer model for large-eddy simulations of turbulent flows with/out pressure gradient
2
2011
... Breuer等[26 ] 从边界层方程出发,考虑了压力梯度的非平衡效应,对WW模型进行了推广. 该方法通过WW模型的幂律速度剖 面构造人工黏性,并通过统计估计定义黏性子层的相对厚度,在周期山状流的数值模拟中准确计算了流动的分离与壁面摩擦力. Duprat等[27 ] 在近壁流动的控制方程中直接考虑了流向压力梯度的非平衡效应,同时以流向压力梯度和壁面摩擦力为特征量, 引入近壁流动的混合特征速度,并以此对壁面单位进行了重新标度. 进一步地,Duprat等[27 ] 依据此混合速度提出了一种近壁涡黏系数衰减的新形式,从而引入了压力梯度对速度剖面和壁面应力 的影响. 相比于仅考虑平衡效应的壁面模型,定义混合速度有效地克服了流动分离点附近的奇异性,并有效地反映了流向压力梯度对流动的影响. 该壁模型准确模拟了周期山状流,尤其在流动的逆压区取得较好的预测结果,数值结果表明在非平衡壁模型中同时考虑了压力梯度和雷诺应力具有重要意义. ...
... [27 ]依据此混合速度提出了一种近壁涡黏系数衰减的新形式,从而引入了压力梯度对速度剖面和壁面应力 的影响. 相比于仅考虑平衡效应的壁面模型,定义混合速度有效地克服了流动分离点附近的奇异性,并有效地反映了流向压力梯度对流动的影响. 该壁模型准确模拟了周期山状流,尤其在流动的逆压区取得较好的预测结果,数值结果表明在非平衡壁模型中同时考虑了压力梯度和雷诺应力具有重要意义. ...
Integral wall model for large eddy simulations of wall-bounded turbulent flows
1
2015
... Yang等[28 ] 同时考虑了近壁流动的压力梯度效应以及局部加速度和对流效应,并提出积分型壁模型. 该模型首先假设近壁速度剖面由线性过渡为对数函数的多参数形式,并引入线性扰动对平衡层壁面律进行了推广;然后通过匹配条件以及积分边界层方程的物理约束,重构壁面流动的速度分布形式,并由此确定壁面摩擦力. 相比于平衡层模型,该模型同时考虑了控制方程中各非平衡项;相比于双层模型(下文将详述),该模型避免了直接求解边界层方程,因此该模型具有多物理和实现简单的优点,迅速引起了广泛关注. ...
Large eddy simulation wall-modeling based on suboptimal control theory and linear stochastic estimation
2
2001
... Nicoud等[29 ] 提出了通过最优控制理论来确定壁面切应力的方法. 该方法将计算出的平均速度剖面与目标平均速度剖面的偏差作为优化目标,采用一个时间步长内的次优控制策略可以在较粗的网格上得到较为准确的壁面切应力,并以此约束外区大涡模拟达到最优解. 但是该方法在每个时间步都需要大量的迭代来完成优化过程,因此它的成本比在相同的网格上使用显式壁面应力模型大20倍. 此外,该方法还必须提供目标平均速度剖面用来确定目标函数. 为了克服这些缺点,Nicoud等[29 ] 提出了线性随机估计形式的壁面应力模型,该模型可以通过局部速度场显式预测壁面切应力,其中的模型系数通过次优控制策略得到的数据确定. 槽道湍流数值模拟的结果表明由该方法推导出的壁模型可以在较粗的网格上准确预测高雷诺数流动的平均速度剖面. 最近,Bae等[30 ,31 ,32 ,33 ] 提出了滑移边界条件修正壁面应力边界条件可能引起的对数区速度匹配问题. ...
... [29 ]提出了线性随机估计形式的壁面应力模型,该模型可以通过局部速度场显式预测壁面切应力,其中的模型系数通过次优控制策略得到的数据确定. 槽道湍流数值模拟的结果表明由该方法推导出的壁模型可以在较粗的网格上准确预测高雷诺数流动的平均速度剖面. 最近,Bae等[30 ,31 ,32 ,33 ] 提出了滑移边界条件修正壁面应力边界条件可能引起的对数区速度匹配问题. ...
Turbulence intensities in large-eddy simulation of wall-bounded flows
1
2018
... Nicoud等[29 ] 提出了通过最优控制理论来确定壁面切应力的方法. 该方法将计算出的平均速度剖面与目标平均速度剖面的偏差作为优化目标,采用一个时间步长内的次优控制策略可以在较粗的网格上得到较为准确的壁面切应力,并以此约束外区大涡模拟达到最优解. 但是该方法在每个时间步都需要大量的迭代来完成优化过程,因此它的成本比在相同的网格上使用显式壁面应力模型大20倍. 此外,该方法还必须提供目标平均速度剖面用来确定目标函数. 为了克服这些缺点,Nicoud等[29 ] 提出了线性随机估计形式的壁面应力模型,该模型可以通过局部速度场显式预测壁面切应力,其中的模型系数通过次优控制策略得到的数据确定. 槽道湍流数值模拟的结果表明由该方法推导出的壁模型可以在较粗的网格上准确预测高雷诺数流动的平均速度剖面. 最近,Bae等[30 ,31 ,32 ,33 ] 提出了滑移边界条件修正壁面应力边界条件可能引起的对数区速度匹配问题. ...
Investigation of the slip boundary condition in wall-modeled LES//Annual Research Briefs 2016
1
2016
... Nicoud等[29 ] 提出了通过最优控制理论来确定壁面切应力的方法. 该方法将计算出的平均速度剖面与目标平均速度剖面的偏差作为优化目标,采用一个时间步长内的次优控制策略可以在较粗的网格上得到较为准确的壁面切应力,并以此约束外区大涡模拟达到最优解. 但是该方法在每个时间步都需要大量的迭代来完成优化过程,因此它的成本比在相同的网格上使用显式壁面应力模型大20倍. 此外,该方法还必须提供目标平均速度剖面用来确定目标函数. 为了克服这些缺点,Nicoud等[29 ] 提出了线性随机估计形式的壁面应力模型,该模型可以通过局部速度场显式预测壁面切应力,其中的模型系数通过次优控制策略得到的数据确定. 槽道湍流数值模拟的结果表明由该方法推导出的壁模型可以在较粗的网格上准确预测高雷诺数流动的平均速度剖面. 最近,Bae等[30 ,31 ,32 ,33 ] 提出了滑移边界条件修正壁面应力边界条件可能引起的对数区速度匹配问题. ...
A physics-based interpretation of the slip-wall LES model//Annual ResearchBriefs 2016
1
2016
... Nicoud等[29 ] 提出了通过最优控制理论来确定壁面切应力的方法. 该方法将计算出的平均速度剖面与目标平均速度剖面的偏差作为优化目标,采用一个时间步长内的次优控制策略可以在较粗的网格上得到较为准确的壁面切应力,并以此约束外区大涡模拟达到最优解. 但是该方法在每个时间步都需要大量的迭代来完成优化过程,因此它的成本比在相同的网格上使用显式壁面应力模型大20倍. 此外,该方法还必须提供目标平均速度剖面用来确定目标函数. 为了克服这些缺点,Nicoud等[29 ] 提出了线性随机估计形式的壁面应力模型,该模型可以通过局部速度场显式预测壁面切应力,其中的模型系数通过次优控制策略得到的数据确定. 槽道湍流数值模拟的结果表明由该方法推导出的壁模型可以在较粗的网格上准确预测高雷诺数流动的平均速度剖面. 最近,Bae等[30 ,31 ,32 ,33 ] 提出了滑移边界条件修正壁面应力边界条件可能引起的对数区速度匹配问题. ...
Dynamic wall models for the slip boundary condition//Annual Research Briefs 2017
1
... Nicoud等[29 ] 提出了通过最优控制理论来确定壁面切应力的方法. 该方法将计算出的平均速度剖面与目标平均速度剖面的偏差作为优化目标,采用一个时间步长内的次优控制策略可以在较粗的网格上得到较为准确的壁面切应力,并以此约束外区大涡模拟达到最优解. 但是该方法在每个时间步都需要大量的迭代来完成优化过程,因此它的成本比在相同的网格上使用显式壁面应力模型大20倍. 此外,该方法还必须提供目标平均速度剖面用来确定目标函数. 为了克服这些缺点,Nicoud等[29 ] 提出了线性随机估计形式的壁面应力模型,该模型可以通过局部速度场显式预测壁面切应力,其中的模型系数通过次优控制策略得到的数据确定. 槽道湍流数值模拟的结果表明由该方法推导出的壁模型可以在较粗的网格上准确预测高雷诺数流动的平均速度剖面. 最近,Bae等[30 ,31 ,32 ,33 ] 提出了滑移边界条件修正壁面应力边界条件可能引起的对数区速度匹配问题. ...
Two-layer approximate boundary conditions for large-eddy simulations
2
1996
... 另外一种提供壁面应力边界条件的模型是双层模型(two-layer model). 这种模型通过在壁面附近嵌入一套细网格并在细网格上求解简化的流动方程为大涡模拟提供应力边界条件[34 ] ,近壁流动的简化方程常取为雷诺平均后的边界层方程 ...
... 双层模型[34 ] 用于近壁平衡的流动时Karman系数 κ [35 ] 提出了动态Karman系数的修正方法,使得第一层大涡模拟网格上的湍流涡黏 ν t ν S GS
Dynamic wall modeling for large-eddy simulation of complex turbulent flows
2
2002
... 双层模型[34 ] 用于近壁平衡的流动时Karman系数 κ [35 ] 提出了动态Karman系数的修正方法,使得第一层大涡模拟网格上的湍流涡黏 ν t ν S GS
... 其中, y w + [35 ] 将该方法用于机翼绕流中,准确预测了流动分离和再附区. Kawai和Larsson[36 ] 认为,Karman系数 κ κ ̂ κ ̂ . Kawai和Larsson[36 ] 假设Karman系数 κ [37 ] 根据需要被模化的雷诺应力加上可解应力的和为通过Karman系数标准值0.41得到的总应力, 也得到了随壁面法向变化的动态Karman系数 κ . ...
Dynamic non-equilibrium wall-modeling for large eddy simulation at high Reynolds numbers
2
2013
... 其中, y w + [35 ] 将该方法用于机翼绕流中,准确预测了流动分离和再附区. Kawai和Larsson[36 ] 认为,Karman系数 κ κ ̂ κ ̂ . Kawai和Larsson[36 ] 假设Karman系数 κ [37 ] 根据需要被模化的雷诺应力加上可解应力的和为通过Karman系数标准值0.41得到的总应力, 也得到了随壁面法向变化的动态Karman系数 κ . ...
... [36 ]假设Karman系数 κ [37 ] 根据需要被模化的雷诺应力加上可解应力的和为通过Karman系数标准值0.41得到的总应力, 也得到了随壁面法向变化的动态Karman系数 κ . ...
An improved dynamic non-equilibrium wall-model for large eddy simulation
1
2014
... 其中, y w + [35 ] 将该方法用于机翼绕流中,准确预测了流动分离和再附区. Kawai和Larsson[36 ] 认为,Karman系数 κ κ ̂ κ ̂ . Kawai和Larsson[36 ] 假设Karman系数 κ [37 ] 根据需要被模化的雷诺应力加上可解应力的和为通过Karman系数标准值0.41得到的总应力, 也得到了随壁面法向变化的动态Karman系数 κ . ...
Numerical aspects and implementation of a two-layer zonal wall model for LES ofcompressible turbulent flows on unstructured meshes
1
2016
... 由上可以看到,双层模型比基于壁面律的壁面应力模型更易考虑非平衡效应,但其应用过程也相应 比较复杂. 与双层模型相 关的综述或介绍可参见文献[9 ,38 -40 ] . ...
湍流大涡数值模拟进展
1
2004
... 由上可以看到,双层模型比基于壁面律的壁面应力模型更易考虑非平衡效应,但其应用过程也相应 比较复杂. 与双层模型相 关的综述或介绍可参见文献[9 ,38 -40 ] . ...
湍流大涡数值模拟进展
1
2004
... 由上可以看到,双层模型比基于壁面律的壁面应力模型更易考虑非平衡效应,但其应用过程也相应 比较复杂. 与双层模型相 关的综述或介绍可参见文献[9 ,38 -40 ] . ...
Towards a generalised dual-mesh hybrid LES/RANS framework with improved consistency
1
2017
... 周期山状流是ERCOFTAC/IAHR(欧洲湍流与燃烧研究机构)设计的LES的测试算例,被广泛用于数值方法和湍流模型的研究[41 ,42 ,43 ,44 ] . 该算例所用的工况为槽道中周期性放置山状障碍,其中山的高度为 h 9 h 3.035 h 4.5 h . 雷诺数( Re = U b h / ν ) 为10 595,其中 U b h U b 图4 给出了周期山状流平均速度的流线以及不同流向位置处的平均流向速度剖面. ...
Investigation of the sensitivity of turbulent closures and coupling of hybrid RANS-LES models for predicting flow fields with separation and reattachment
1
2017
... 周期山状流是ERCOFTAC/IAHR(欧洲湍流与燃烧研究机构)设计的LES的测试算例,被广泛用于数值方法和湍流模型的研究[41 ,42 ,43 ,44 ] . 该算例所用的工况为槽道中周期性放置山状障碍,其中山的高度为 h 9 h 3.035 h 4.5 h . 雷诺数( Re = U b h / ν ) 为10 595,其中 U b h U b 图4 给出了周期山状流平均速度的流线以及不同流向位置处的平均流向速度剖面. ...
Comparison of a spectral method with volume penalization and a finite volume method with body fitted grids for turbulent flows
1
2016
... 周期山状流是ERCOFTAC/IAHR(欧洲湍流与燃烧研究机构)设计的LES的测试算例,被广泛用于数值方法和湍流模型的研究[41 ,42 ,43 ,44 ] . 该算例所用的工况为槽道中周期性放置山状障碍,其中山的高度为 h 9 h 3.035 h 4.5 h . 雷诺数( Re = U b h / ν ) 为10 595,其中 U b h U b 图4 给出了周期山状流平均速度的流线以及不同流向位置处的平均流向速度剖面. ...
A priori assessment of prediction confidence for data-driven turbulence modeling
1
2017
... 周期山状流是ERCOFTAC/IAHR(欧洲湍流与燃烧研究机构)设计的LES的测试算例,被广泛用于数值方法和湍流模型的研究[41 ,42 ,43 ,44 ] . 该算例所用的工况为槽道中周期性放置山状障碍,其中山的高度为 h 9 h 3.035 h 4.5 h . 雷诺数( Re = U b h / ν ) 为10 595,其中 U b h U b 图4 给出了周期山状流平均速度的流线以及不同流向位置处的平均流向速度剖面. ...
General circulation experiments with the primitive equations
1
1963
... 需要得到涡黏系数的模型才能求解方程(16). Smagorinsky涡黏模型[45 ] 是大涡模拟中常用的模型之一,它的涡黏系数为 ...
A dynamic subgrid-scale eddy viscosity model
1
1991
... 为了解决这个问题,Germano等[46 ] 发展了确定系数 C s 2 Δ ̅ Δ ̅ ∧ . 同时采用该单元与相邻单元内物理量的简单平均得到二次滤波以后的量. 在使用滤波宽度 Δ ̅ τ ij Δ ̅ ∧ T ij τ ij T ij
A proposed modification of the Germanosubgrid-scale closure method
1
1992
... 上式是超定方程,可以采用最小二乘法求解[47 ] ...
Discrete conservation principles in large-eddy simulation with application to separation control over an airfoil
1
2008
... 在 数值模拟中,下壁面设置为无滑移边界条件,流向与展向设置为周期边界条件,上壁面的切应力边界条件由壁模型提供. 时间推进采用分步法,对流项的时间推进采用显式的两步Adams-Bashforth格式,黏性项采用Crank-Nicholson格式. 流场采用非结构网格离散,方程中的空间导数采用有限体积方法离散. 非结构网格可以采用任意形状的单元,因此能够很好地模拟复杂几何边界. 尤其是在非结构网格上结合有限体积方法,可以使计算程序具有很强的通用性. 为了保持数值计算的精度和稳定性, 使用了基于离散动能守恒原理的非结构网格上的离散方法[48 ] . 该方法在计算区域中不产生非物理的能量源,从而可以保持大涡模拟的精度和预测能力. 压力Poisson方程采用代数多重网格方法求解,代数多重网格的求解器为Hypre软件包中的BoomerAMG. ...
Investigation of wall-function approximations and subgrid-scale models in large eddy simulation of separated flow in a channel with streamwise periodic constrictions
8
2003
... 采用 与ERCOFTAC数据库中文献[49 ,50 ] 相同的计算网格:其中流向、法向和展向的网格数目分别为197, 129和186. 需要注意的是, 文献[49 ,50 ] 使用基于结构网格的流场求解器,而本文使用基于非结构网格的流场求解器, 因此该网格预先被处理成非结构网格的形式. 图5 画出了垂直于展向的某一截面上的网格分布,下壁面近壁网格的特征尺度满足 ...
... [49 ,50 ]使用基于结构网格的流场求解器,而本文使用基于非结构网格的流场求解器, 因此该网格预先被处理成非结构网格的形式. 图5 画出了垂直于展向的某一截面上的网格分布,下壁面近壁网格的特征尺度满足 ...
... 图4 画出了平均流场的流线,从中可以看出流动分离、再附和回流区等分离流的物理特征. 流动分离点在 x = 0.2 x = 4.6 [49 ,50 ] 的结果吻合. ...
... 本文在4个截面处比较了计算的平均速度与文献[49 ,50 ]的计算结果以及文献[51 ] 的实验结果,这4个截面分别是位于流动分离点 附近的 x = 0.5 x = 2.0 x = 4.0 x = 6.0 . 图6 对比了平均流向速度 U 图7 对比了平均法向速度 V 49 ,50 ]的计算结果以及文献[51 ] 的实验结果 吻合很好. x = 0.5 图6 (a)所示. 此外,流速在山顶高度附近快速增加,这说明存在流动分离形成的强剪切层. x = 2.0 x = 0.5 图6 (b)所示. x = 4.0 图6 (c)所示. x = 6.0 图6 (d)所示. 此外,图7 (c)和图7 (d)表明 x = 4.0 x = 6.0
... ,本文的计算结果与文献[49 ,50 ]的计算结果以及文献[51 ] 的实验结果 吻合很好. x = 0.5 图6 (a)所示. 此外,流速在山顶高度附近快速增加,这说明存在流动分离形成的强剪切层. x = 2.0 x = 0.5 图6 (b)所示. x = 4.0 图6 (c)所示. x = 6.0 图6 (d)所示. 此外,图7 (c)和图7 (d)表明 x = 4.0 x = 6.0
... 进一步地比较 x = 0.5 x = 2.0 x = 6.0 图8 比较了流向脉动速度的二阶统计量 u ' u ' 图9 比较了法向脉动速度的二阶统计量 v ' v ' 图10 比较了雷诺应力 u ' v ' . 本文的结果与文献[49 ,50 ] 的计算结果以及文献[51 ] 的实验结果吻合很好. x = 0.5 图8 (a)和图10 (a)所示. 从图8 (b)、图9 (b)以及图10 (b)可以看出,由于存在剪切, x = 2.0 图6 (d)表明 x = 6.0 图8 (c), 图9 (c)以及图10 (c)可以看出, x = 6.0 x = 2.0
... 本文所得到的下壁面摩擦系数的结果与文献[49 ,50 ]的结果一致,如图11 (a)所示. 下壁面摩擦系数在流动分离点( x = 0.2 x = 4.6 x = 2.6 x = 8.6
... 图11 (b)比较了下壁面的压力系数 C p 49 ,50 ]的结果吻合较好,在流动恢复段有约 5 % 图11 (b)可以看出,压力系数在山顶后陡升,形成逆压梯度从而引起分离,接着压力系数在回流区的前半部分( x = 0.5 x = 2.0 x = 7.6 x = 8.7
Highly resolved large-eddy simulation of separated flow in a channel with streamwise periodic constrictions
8
2005
... 采用 与ERCOFTAC数据库中文献[49 ,50 ] 相同的计算网格:其中流向、法向和展向的网格数目分别为197, 129和186. 需要注意的是, 文献[49 ,50 ] 使用基于结构网格的流场求解器,而本文使用基于非结构网格的流场求解器, 因此该网格预先被处理成非结构网格的形式. 图5 画出了垂直于展向的某一截面上的网格分布,下壁面近壁网格的特征尺度满足 ...
... ,50 ]使用基于结构网格的流场求解器,而本文使用基于非结构网格的流场求解器, 因此该网格预先被处理成非结构网格的形式. 图5 画出了垂直于展向的某一截面上的网格分布,下壁面近壁网格的特征尺度满足 ...
... 图4 画出了平均流场的流线,从中可以看出流动分离、再附和回流区等分离流的物理特征. 流动分离点在 x = 0.2 x = 4.6 [49 ,50 ] 的结果吻合. ...
... 本文在4个截面处比较了计算的平均速度与文献[49 ,50 ]的计算结果以及文献[51 ] 的实验结果,这4个截面分别是位于流动分离点 附近的 x = 0.5 x = 2.0 x = 4.0 x = 6.0 . 图6 对比了平均流向速度 U 图7 对比了平均法向速度 V 49 ,50 ]的计算结果以及文献[51 ] 的实验结果 吻合很好. x = 0.5 图6 (a)所示. 此外,流速在山顶高度附近快速增加,这说明存在流动分离形成的强剪切层. x = 2.0 x = 0.5 图6 (b)所示. x = 4.0 图6 (c)所示. x = 6.0 图6 (d)所示. 此外,图7 (c)和图7 (d)表明 x = 4.0 x = 6.0
... ,50 ]的计算结果以及文献[51 ] 的实验结果 吻合很好. x = 0.5 图6 (a)所示. 此外,流速在山顶高度附近快速增加,这说明存在流动分离形成的强剪切层. x = 2.0 x = 0.5 图6 (b)所示. x = 4.0 图6 (c)所示. x = 6.0 图6 (d)所示. 此外,图7 (c)和图7 (d)表明 x = 4.0 x = 6.0
... 进一步地比较 x = 0.5 x = 2.0 x = 6.0 图8 比较了流向脉动速度的二阶统计量 u ' u ' 图9 比较了法向脉动速度的二阶统计量 v ' v ' 图10 比较了雷诺应力 u ' v ' . 本文的结果与文献[49 ,50 ] 的计算结果以及文献[51 ] 的实验结果吻合很好. x = 0.5 图8 (a)和图10 (a)所示. 从图8 (b)、图9 (b)以及图10 (b)可以看出,由于存在剪切, x = 2.0 图6 (d)表明 x = 6.0 图8 (c), 图9 (c)以及图10 (c)可以看出, x = 6.0 x = 2.0
... 本文所得到的下壁面摩擦系数的结果与文献[49 ,50 ]的结果一致,如图11 (a)所示. 下壁面摩擦系数在流动分离点( x = 0.2 x = 4.6 x = 2.6 x = 8.6
... 图11 (b)比较了下壁面的压力系数 C p 49 ,50 ]的结果吻合较好,在流动恢复段有约 5 % 图11 (b)可以看出,压力系数在山顶后陡升,形成逆压梯度从而引起分离,接着压力系数在回流区的前半部分( x = 0.5 x = 2.0 x = 7.6 x = 8.7
Flow over periodic hills-numerical and experimental study in a wide range of Reynolds numbers
3
2009
... 本文在4个截面处比较了计算的平均速度与文献[49 ,50 ]的计算结果以及文献[51 ] 的实验结果,这4个截面分别是位于流动分离点 附近的 x = 0.5 x = 2.0 x = 4.0 x = 6.0 . 图6 对比了平均流向速度 U 图7 对比了平均法向速度 V 49 ,50 ]的计算结果以及文献[51 ] 的实验结果 吻合很好. x = 0.5 图6 (a)所示. 此外,流速在山顶高度附近快速增加,这说明存在流动分离形成的强剪切层. x = 2.0 x = 0.5 图6 (b)所示. x = 4.0 图6 (c)所示. x = 6.0 图6 (d)所示. 此外,图7 (c)和图7 (d)表明 x = 4.0 x = 6.0
... [51 ]的实验结果 吻合很好. x = 0.5 图6 (a)所示. 此外,流速在山顶高度附近快速增加,这说明存在流动分离形成的强剪切层. x = 2.0 x = 0.5 图6 (b)所示. x = 4.0 图6 (c)所示. x = 6.0 图6 (d)所示. 此外,图7 (c)和图7 (d)表明 x = 4.0 x = 6.0
... 进一步地比较 x = 0.5 x = 2.0 x = 6.0 图8 比较了流向脉动速度的二阶统计量 u ' u ' 图9 比较了法向脉动速度的二阶统计量 v ' v ' 图10 比较了雷诺应力 u ' v ' . 本文的结果与文献[49 ,50 ] 的计算结果以及文献[51 ] 的实验结果吻合很好. x = 0.5 图8 (a)和图10 (a)所示. 从图8 (b)、图9 (b)以及图10 (b)可以看出,由于存在剪切, x = 2.0 图6 (d)表明 x = 6.0 图8 (c), 图9 (c)以及图10 (c)可以看出, x = 6.0 x = 2.0
Space-time correlations and dynamic coupling in turbulent flows
1
2017
... 由于WW模型属于平衡层模型,而周期山状流下壁面附近存在流动分离、再附以及回流等压力梯度不能忽略的非平衡现象,因此 当前的工作在下壁面附近使用了能够解析壁面层的网格. 为了进一步减少计算量,可以在下壁面附近使用不能解析壁面层的网格,那就需要能够适用于分离流等复杂流动的壁模型,这是现在一个活跃的研究领域. 本文提到的考虑了压力梯度等非平衡效应的各种壁模型应该被广泛测试,以加深对这些模型适用范围的认识. 最后,当考虑湍流噪声问题, 需要精准计算壁面附近流动的时空关联,因此需要发展时间精准的壁模型[52 ] . ...