引 言
多孔介质与自由流组成的复合流体通道包括三个区域:多孔介质区、自由流体区及二者界面区,研究其内流体的流动与传热传质现象在许多工程实际中有着广泛应用价值,如石油开采、水资源利用、地热工程、地下水流动、核废料处置、太阳能集热器、干燥技术、化学反应器、热交换器等.
由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力.
综上所述,由于多孔介质-自由流耦合通道具有复杂的界面结构,在前人研究过程中,除了研究的几何模型不同之外,多孔介质内部以及多孔介质与自由流体区界面处采用的动量传递模型也有较大区别,但可以肯定的是,界面效应是不可忽略的. 当采用界面应力跳跃模型时,不仅能够体现界面处速度及剪切应力均连续的界面模型(当取界面跳跃系数为0时),也可以解决B-J界面模型界面速度不连续问题,且适当调整界面应力系数可与Beavers和Joseph$^{[1]}$的实验结果吻合良好,因此在界面处采用界面应力跳跃模型有更好的适用性且更符合实际现象. 目前为止,大多学者采用数值方法对复合流进行研究,不能直接反映出界面效应的影响;也有较少学者得到了对称通道内,界面应力跳跃系数与界面速度的解析关系式,或采用连续应力条件得到了非对称通道内界面速度解析式. 对于采用应力跳跃界面条件,对非对称多孔介质复合通道内的流体流动特性(包括界面速度与流体摩擦系数)进行解析解的分析研究还尚未发现. 因此,本文采用Brinkman-extended
Darcy多孔介质模型并结合速度连续、剪切应力跳跃的界面条件对部分填充多孔介质非对称平行复合通道内的流体流动特性进行推导求解,获得考虑界面应力跳跃时非对称复合通道各区域流体运动速度及摩擦系数的解析式,并进一步分析研究具有不同渗透特性、不同填充厚度多孔层及界面应力跳跃系数对流动分布及阻力特性的影响,以期为工程实际提供理论参考数据.
1 动力学模型
1.1复合通道物理模型
考虑研究的物理模型为部分填充多孔介质层的平行平板复合通道,如图1 所示.上层为自由流体区域,下层为多孔介质区域,二者相 交处为界面,上下层均受非渗透性固体壁面边界条件限制.通道总高度设为2$H$,界面处距离通道中心线处为 $\gamma H$,则有 $\gamma $值取$-1$到1之间,为多孔介质无量纲偏心厚度.多孔层特性为各向同性,渗透率为一常数,假设流经此模型的流体状态为不可压缩层流且充分发展.
图1 流体通道物理模型
Fig. 1 Physical model of the fluid flow channel
1.2 复合通道数学模型及解析解
假定通道内流体运动状态为水平压力梯度dp =dx 驱动的充分发展层流状态,则自由流体区内流体运动方程为
$$ \dfrac{\d^2u_{\rm f} }{\d y^2} - \dfrac{1}{\mu _{\rm f} }\dfrac{\d p}{\d x} = 0 (1) $$
其中, $u_{\rm f} $ 表示通道内自由流体区域中的流体速度(下标``f''表示 自由流体),$\mu_{\rm f}
$是流体动力黏度, $p$是压力. 多孔介质区内流体运动方程为
$$ \mu _{\rm eff} \dfrac{\d^2u_{\rm p} }{\d y^2} - \dfrac{\mu _{\rm f} }{k}u_{\rm p} - \dfrac{\d p}{\d x} - \dfrac{C_{\rm f} \rho u_{\rm P}^2}{\sqrt k } = 0 (2) $$
其中,$\mu_{\rm eff}$是多孔介质的有效动力黏度,是与Brinkman项有关的参数,其不仅是多孔介质孔隙率的函数,也与多孔介质几何结构密切相关$^{[31]}$. $u_{\rm p}$表示多孔层内的流体速度(下标``p''表示多孔层通道), $\rho $ 是流体密度,$k$和$C_{\rm f}$分别是多孔介质渗透率和惯性系数. 该方程中的第一项是涉及与流体运动相关的壁效应,当多孔介质流区域包含界面时,Brinkman项则显得更为重要,因为它能够反映边界层的发展变化. 第二项及第三项与Darcy定律相关,第四项则涉及Forchheimer惯性效应. 对于某些工程应用而言,基于多孔层内固体颗粒粒径的雷诺数较小,意味着在某些涉及多孔介质的实际应用中可以忽略Forchheimer惯性效应,因此,本文将暂不考虑Forchheimer惯性项的影响. 上下非渗透性固体壁面处采用无滑移速度边界条件
$$ \left. {u_{\rm f} } \right|_{y = H} = \left. {u_{\rm p} } \right|_{y = - H} = 0 (3) $$
自由流体区与多孔介质区界面处采用速度连续,应力跳跃模型$^{[13]}$,为
\vskip 2mm $\left. {u_{\rm f} } \right|_{y = \gamma H} = \left. {u_{\rm p} } \right|_{y = \gamma H} = u_{\rm i} \hfill (4)$
\vskip 2mm $\left. {\mu _{\rm eff} \dfrac{ \d u_{\rm p} }{\d y}} \right|_{y = \gamma H} - \left. {\mu _{\rm f} \dfrac{\d u_{\rm f} }{\d y}} \right|_{y = \gamma H} = - \beta \dfrac{\mu _{\rm f} }{\sqrt k }u_{\rm f} \hfill (5)$
其中, β [ - 1,1.5 ] [13,15 ] ,是与多孔介质孔隙率、渗透率和孔径 等多种因素密切相关的界面动量分配系数,需通过实验进行确定. 当 β = 0 u i G = - ∂ p ∂ x U = μ f uG H 2 M = μ e ff μ f Da = k H 2 R = 1 MDa . 其中,较多学者在应用Brinkman-extended Darcy模型时认为 μ e ff = μ f [32 ] 通过实验研究指出在某些情况下区分这两个参数是十分重要的,并建议 μ e ff = ( 7 . 5 - 2.4 + 3.4 ) μ f . Ochoa-Tapia和Whitaker [13,15 ] 在研究复合通道多孔介质流时则采用关系式 μ e ff = μ f / ε ε [33 ] 研究发现当 μ e ff / μ f ~ 7.5 范围内变化时,对复合通道内流体的速度分布影响较小. 因此,本文将暂不考虑 M μ e ff = μ f / ε μ e ff ε = 0.6 M = 1 / 0.6 . 将上述流体运动控制方程(1) ~ (5) 改写成无量纲形式,可得自由流体区与多孔介质区内流体无量纲运动方程分别为
$ {\d^2U_{\rm f} }{\d Y^2} + 1 = 0 (6) $
$ \dfrac{\d^2U_{\rm p}}{\d Y^2} - R^2U_{\rm p} + \dfrac{1}{M} = 0 (7) $
无量纲边界条件为
U f Y = 1 = U p Y = - 1 = 0 ( 8 )
U f Y = γ = U p Y = γ = U i ( 9 )
M d U p d Y Y = γ - d U f d Y Y = γ = - β 1 Da U f Y = γ ( 10 )
联立方程(6) ~ (9) 可求得
当 - 1 # x 2264 ; Y # x 2264 ; γ
U p = N 0 + N 1 sinh R γ - Y + 2 mm ] N 2 sinh R Y + 1 ( 11 )
当 γ # x 2264 ; Y # x 2264 ; 1
U f = C 0 + C 1 Y + C 2 Y 2 ( 12 )
其中
$\left.\!\ N_0 = {1}{MR^2}\,, \quad N_1 = - \dfrac{1}{MR^2\sinh \left[ {R\left( {1 + \gamma } \right)} \right]} \\ N_2 = \dfrac{\left( {MU_{\rm i} R^2 - 1} \right)}{MR^2\sinh \left[{R\left( {1 + \gamma } \right)} \right]} \!\!\right\} (13a)$
$ C_0 = \dfrac{\gamma - 2U_{\rm i} - \gamma ^2}{2(\gamma - 1)}\,, \ \ C_1 = \dfrac{2U_{\rm i} +\gamma ^2 - 1}{2(\gamma - 1)}\,, \ \ C_2 = - \dfrac{1}{2} (13b)$
发现式(13)中包含未知数 U i . 为了求得界面速度 U i
$U_{\rm i} = \Bigg \{ \dfrac{1}{R\tanh \left[ {R\left( {1 + \gamma } \right)} \right]} - \dfrac{1}{R\sinh \left[ {R\left( {1 + \gamma } \right)} \right]} + \dfrac{1 -\gamma }{2} \Bigg \} \Bigg / \qquad \Bigg \{ \dfrac{MR}{\tanh \left[ {R\left( {1 + \gamma } \right)} \right]} - \dfrac{\beta - \beta \gamma + \sqrt {Da} }{\sqrt {Da} \left( {\gamma - 1} \right)} \Bigg \} (14)$
将式(13)和式(14)代入式(11)和式(12)中,可分别得到多孔介质区内及自由流体区域内流体运动速度分布解析解. 进一步定义平均速度
U m = 12 ∫ - 1 1 U d Y = 12 ∫ - 1 γ U p Y d Y + ∫ γ 1 U f Y d Y
则根据上述结果可整理得平均速度
$ U_{\rm m} = \Bigg[ N_0 \left( {\gamma + 1} \right) + \dfrac{N_1 + N_2 }{R}\left( {\cosh \left( {R\left( {1 + \gamma } \right)} \right) - 1} \right) +$ \vskip 2mm \n \ \ $ \qquad c_0 \left( {1 - \gamma } \right) + \dfrac{c_1 }{2}\left( {1 - \gamma ^2} \right) + \dfrac{c_2 }{3}\left( {1 - \gamma ^3} \right) \Bigg ] \Bigg /{2} \hfill (15)$
常数 N 0 N 1 N 2 C 0 C 1 C 2 U ̂
$$ \hat {U} = \dfrac{U}{U_{\rm m} } (16) $$
由摩擦系数定义 f = 2 H - d p d x / ( 1 / 2 ρ u m 2 )
$$ f Re = \dfrac{8}{U_{\rm m} } (17) $$
其中 Re = ρ u m 2 H / μ f .
2 解析解模型验证
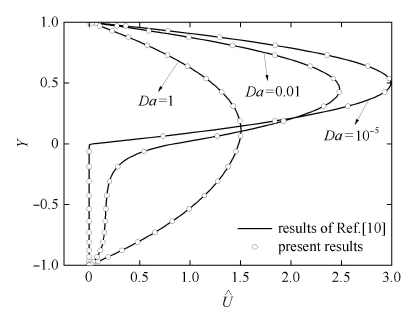
将本文所得解析解模型进行计算,并与文献[10 ]在相同工况下的解析结果进行对比,发现不考虑界面应力跳跃时,即多孔 介质--自由流界面采用速度及剪切应力均为连续模型时,文献[10 ]的解析结果与本文在跳跃系数 β = 0 图2 所示,文献[10 ]提出的解析解为本文所得结果模型的一个特例,证明了本文结果模 型的正确性. 而由前人研究可知 [16 ] ,在某些情况下,界面效应是不可忽略的,特别是界面处固体颗粒对流体动量的非连续影响,利 用本文给出的解析解模型可以更客观的描述考虑界面应力跳跃情况下的多孔介质--自由流耦合通道的流动特性, 从而拓宽及完善非对称多孔介质--自由流耦合通道内复杂界面流体流动特性解析解的应用条件.
图2 本文结果与文献[10 ]结果比较
Fig. 2 Comparison between present result and Ref.[10] result
3 计算结果分析与讨论
3.1 γ = 0 β
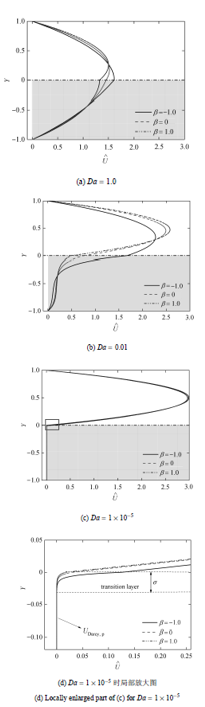
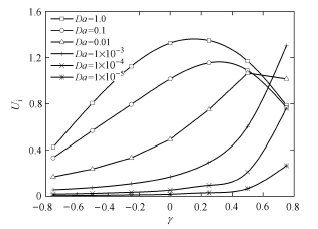
当多孔层偏心厚度 γ = 0 H . 图3 所示为 Da β β = 0 Da Da = 1 β = 0 Da Da = 0.01 Da = 1 × 1 0 - 5 Da
图3 不同Da 下,β
Fig. 3 The effect of β Da
对于Da = 0.01 的多孔介质层(图3 (b)),相较于Da = 1.0 及 Da = 1 × 1 0 - 5 图3 (a)(c))而言,界面应力系数 β β β Da = 1.0的多孔层也出现此定值速度,但 Da = 1.0 时随界面应力系数 β
对于渗透性更小的多孔介质层,即Da =10 - 5 时(图3 (c)),界面处的速度也会随 β Da =1.0及Da =0.01时的情况. 所不同的是,由于插入的较小渗透率多孔层,会更大程度地阻碍流体在其内的运动,会在距界面很小范围内就将流体速度制止,使流速基本趋于0,并在多孔介质内形成一个不随高度变化的很小的固定速度值,即Darcy速度,一般将界面位置到刚出现Darcy速 度时的通道高度 σ 27 ]给出的多孔介质分区模型相同, 如图3 (d)所示,而由于质量守恒,使自由流体区具有更大的流体速度. 此时改变界面应力系数 β Da =1.0及Da =0.01的多孔介质层而言较小,而Da =1.0的多孔层又小于Da =0.01的多孔介质层. 因此, γ Da 的多孔层,改变界面性质可明显控制多孔层及自由流体层内的流体速度分布.
图4 所示为复合通道界面应力系数 β U i β U i Da = 1 1 × 1 0 - 5 β = - 1.0 → 1.5 U i → 1.269 , 1.676 → 0.417 , 0.126 → 0.014 , 根据式子 Δ U i / U i , max U i Da 的减小而增大,但具有中间范围Da 的多孔层会出现 更大范围 U i β < 0
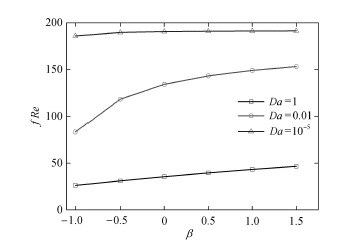
图5 所示为复合通道界面应力系数 β fRe Da 下,增大复 合通 道界面应力系数 β fRe 的不断增大,意味着流体流动所受到的压降阻力会不断增大. 而对于拥有Da 较小的多孔层的复合通道,如 Da = 1 × 1 0 - 5 β Da 多孔层的复合通道,流体流动时所受到的阻力压降较小,且随界面应力系数的增大而变化不大;而对于中间范围Da 的多孔层而言,随 β fRe 值增加近两倍,且在 β < 0
图4 应力系数与界面速度关系
Fig. 4 The relation between stress jump coefficient and interfacial velocity
图5 应力系数与摩擦系数关系
Fig. 5 The relation between stress jump coefficient and friction coefficient
3.2 γ β
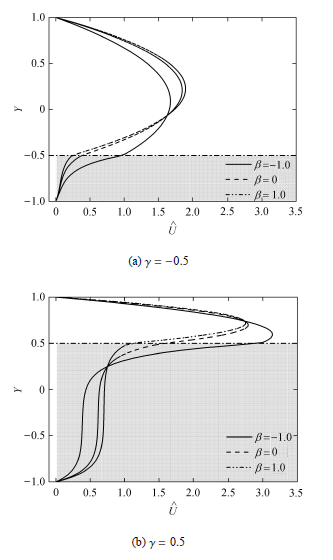
多孔层偏心厚度 γ 图1 所示,可得二者关系式为 ( 1 + γ ) H . 由关系式可知,多孔层偏心厚度 γ 图3 (b),考虑 Da = 0.01 γ = - 0.5 1 / 2 H H 3 / 2 H β 图6 所示. 随着填充多孔层厚度的增大,自由流体区内、多孔介质区内及二者界面处的最大流体速度均在不断增大. 但需要注意的是,改变 β γ = - 0.5 β γ > 0.5 图7 所示.
图6 不同多孔层偏心厚度下,β
Fig. 6 The effect of β
图7 Da = 0.01 β γ U i
Fig. 7 The relation between porous off-center thickness γ U i β Da = 0.01
为了验证是否任一Da 下都会出现这种现象. 以 β = 1 图8 . 由图8 发现, 当Da 较小时,填充多孔层偏心厚度 γ U i γ Da 较大时,并不是填充的多孔层厚度越厚界面速度就会越大,而会出现一个最佳填充厚度使界面速度达到最大,并且此最佳 厚度会随着Da 的增大而减小. 分析认为,这是由于在通道内填充多孔介质层,一方面会增大流体流动阻力,另一方面使流体自由流动通道截面积降低,根据质量守恒,会使自由流体通道内的流体流动速度增大. 这两方面因素共同作用就会出现当多孔层偏心厚度达到一定值时,或多孔层厚度填充到一定值时,界面处速度继续增大或减小的情况.
图8 β = 1 Da 下,多孔层偏心厚度 γ U i
Fig. 8 The relation between porous off-center thickness γ U i Da β = 1
由于界面存在情况下, β [ - 1.0 1.5 ] γ ( - 1,1 ) [ - 0.8,0.8 ] Da 为横坐标,进一步研究不同Da 下, β γ U i
图9 及图10 分别为固定 γ / β [ - 0.8,0.8 ] β / γ Da 与界面速度 U i 图9 (a)为 γ = - 0.8 γ = 0.8 β Da 与界面速度 U i β = - 0.8 图9 (b)为 γ = - 0.5 γ = 0.5 β Da U i β = - 0.8 图9 可以看出,当 γ = - 0.8 β - 0.8 → 0 → 0.8 Da 下 U i Δ U i γ - 0.8 → - 0.5 → 0.5 → 0.8 β - 0.8 → 0 → 0.8 Da 下的 U i γ = 0.8 β Da 下 U i 2 / 3 U i , max . 另外,还可以发现,较低 γ U i Da 的增大而单调增大,一定范围的Da 对 U i Δ Da γ U i γ Da 下移 动,造成 Δ Da Da 的多孔层会出现更大范围 U i β < 0 U i 图4 中 γ = 0
图9 γ β Da 与界面速度U i
Fig. 9 The relation between Da and interfacial velocity when changing β γ
图10 为 β = ± 0.8 β = ± 0.5 γ Da 与界面速度 U i γ = - 0.8 图10 可以看出, β U i γ Da 下出现交点. 在交点之前,每组曲线值 U i γ U i γ 图8 的结果一致. 随着 β γ U i Da 下会不断减小,且在较大 γ U i 图9 结果一致. 结合图9 ,可以得出:当 γ β γ U i β γ β β U i γ
图10 β γ Da 与界面速度U i
Fig. 10 The relation between Da and interfacial velocity U i γ β
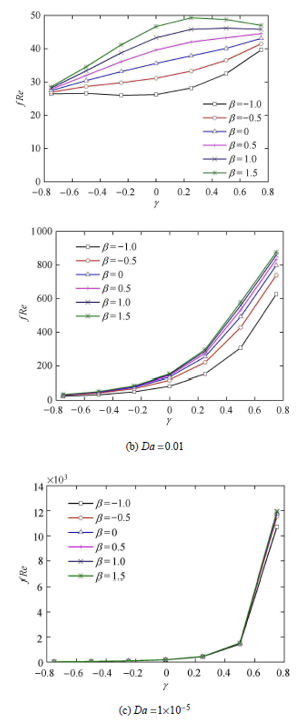
进一步研究不同Da 下, β γ fRe 的影响. 由于Da 对fRe 的影 响通常在几个数量级,若以Da 为横坐标则不能清晰的表示 β γ fRe 的影响. 因此,分别得出Da =1.0,0.01,1 × 10 - 5 时,不同界面应力系数 β γ fRe 的影响,如图11 所示. 在相同部分填充多孔介质层通道内,随着Da 的不断减小(图11 (a) → 图11 (c)),流体运动摩擦系数fRe 将不断增大,且增大幅度会因多孔层厚度的增加而急剧变大. 发现当Da 数及多孔层偏心厚度一定时,fRe 都会随界面应力系数 β β < 0 Da =1 × 10 - 5 时的增大范围很小,以至于可以粗略认为重合于一点. 对于Da =0.01及Da =1 × 10 - 5 的多孔层,即使 β fRe 也一致出现随 γ γ fRe 对 γ Da =1.0的多孔层,在 β = - 1.0 fRe 值随 γ β fRe 值则同Da =0.01及Da =1 × 10 - 5 的多孔层一样随 γ β fRe 值随 γ Da 下随 β fRe 呈现出不同的变化规律, γ β fRe 的影响均较大;但随着Da 的不断减小, γ fRe 的影响要大于 β Da 小到一定程度时(Da =1 × 10 - 5 ), β fRe 的影响可忽略不计而认为只与 γ fRe 对较大 γ
图11 不同β γ fRe 的关系
Fig. 11 The relation between porous off-center thickness γ fRe with different β
4 与B-J速度滑移界面模型的比较
根据Beavers和Joseph [1 ] 提出的B-J速度滑移界面模型,有如下方程
$$ \left. {\frac{d u_{\rm f} }{d y}} \right|_{y = \gamma H} = \dfrac{\alpha ^\ast }{\sqrt k }\left( {u_{\rm i} - u_{\rm p} } \right) (18) $$
其中, α * ~ 4 ,主要受界面处多孔介质结构性质、雷诺数等的影响 [1 ] ,与应力跳跃系数 β [2,34-35 ] . 在多孔层内流体运动符合Darcy定律,即不考虑Brinkman项及Forchheimer项,方程(2)变为
$$ -\dfrac{\mu _{\rm f} }{k}u_{\rm p} - \dfrac{\d p}{\d x} = 0 (19) $$
自由流体区内的流体运动方程仍为方程(1)且仍有边界条件 u f y = H = 0 . 将上述方程无量纲化后,可求得方程组解为
U p = Da
$$ U_{\rm f} = - \dfrac{\left( {Y - \gamma } \right)^2}{2} + \dfrac{\alpha ^\ast }{\sqrt {Da} }\left( {U_{\rm i} - Da} \right)\left( {Y - \gamma } \right) + U_{\rm i} $$
其中界面处速度为
$$ U_{\rm i}= \dfrac{\dfrac{1}{2}\left( {1 - \gamma } \right)^2 + \alpha ^\ast \sqrt {Da} \left( {1 - \gamma } \right)}{\alpha ^\ast \left( {1 - \gamma } \right) / \sqrt {Da} + 1} $$
进一步可通过平均速度的定义求得
$$ \bal U_{\rm m}= \Bigg[ Da\left( {1 + \gamma } \right) - \dfrac{1}{6}\left( {1 - \gamma } \right)^3 +\[2mm] \qquad \dfrac{\alpha ^\ast }{2\sqrt {Da} }\left( {U_{\rm i} - Da} \right)\left( {1 - \gamma } \right)^2 + U_{\rm i} \left( {1 - \gamma } \right) \Bigg ] \Big / {2} \eal $$
最终可得各区域无量纲速度$\hat {U} = \dfrac{U}{U_{\rm m}}$.
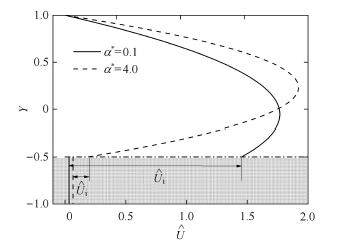
图12 所示为Da =0.01, γ = - 0.5 α * Y = γ Y = - 1.0 ) 均出现了速度不连续现象. α * U ̂ i α * ( Y = - 1.0 ) α * 图6 (a)进行比较,可以看出采用Brinkman-extended Darcy模型并结合Ochoa-Tapia和Whitaker [13 ] 提出的界面条件能够很好的解决B-J速度滑移条件下的速度不连续问题,不仅能够使与自由流体区接触界面处速度连续,也能保证与多孔介质接触的非渗透性固体壁面处速度为0,更符合实际现象. 另外,Ochoa-Tapia和Whitaker [13,15 ] 指出,在利用复杂体积平均方法推导界面模型时,Brinkman-extended Darcy模型与Stokes’方程的匹配过程要求同时保证应力不连续及速度连续.
图12 γ = - 0.5 α *
Fig. 12 The effect of α * γ = - 0.5
5 结 论
采用Brinkman-extended Darcy模型并结合速度连续,剪切应力跳跃的界面条件对非对称多孔介质--自由流复合通道内多孔介质内部及多孔介质与自由流体界面处复杂质量、动量输运特性进行研究,得到考虑多 孔介质界面处应力跳跃时,复合通道内各区域流体运动速度及摩擦系数的解析式,并根据解析式进一步分析了界面应力系数 β Da 及多孔层偏心厚度 γ Da 范围内改变界面性质可明显控制各区域流体速度分布;(2)在达西数、多孔层偏心厚度一定情况下,随界面应力系数的增大界面 处流速会不断减小,而流体摩擦系数则会不断增大,特别是界面应力系数小于0的情况下变化更加明显,此时若不考虑界面应力 跳跃则会造成较大误差;(3)界面性质确定情况下,当达西数较小时,填充多孔层厚度与界面速度成单调正相关性,且在多孔区 内出现不随 y β γ γ U i β γ β β U i γ Da 下随 β fRe 呈现出不同的变化规律, γ β fRe 的影响均较大;继续减小达西数直至Da 小到一定程度时, β fRe 的影响可忽略不计而认为只与 γ fRe 对较大 γ
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
Beavers GS Joseph DD Boundary conditions at a naturally permeable wall
.Journal of Fluid Mechanics , 1967 , 30 (01 ): 197 -207
[本文引用: 4]
[2]
Sahraoui M Kaviany M Slip and no-slip velocity boundary conditions at interface of porous, plain media
.International Journal of Heat & Mass Transfer 1992 , 35 (4 ): 927 -943
[本文引用: 1]
[3]
Chang MH Chen F Straughan B Instability of Poiseuille flow in a fluid overlying a porous layer
. Journal of Fluid Mechanics , 2006 , 564 : 287 -303
[本文引用: 1]
[4]
Cao Y Gunzburger M Hua F et al .Coupled Stokes-Darcy model with Beavers-Joseph interface boundary condition
.Communications in Mathematical Sciences , 2010 , 8 (1 ): 1 -25
[本文引用: 1]
[5]
Cao Y Gunzburger M Hu X et al .Finite element approximations for stokes-darcy flow with beavers-joseph interface conditions
.Siam Journal on Numerical Analysis , 2010 , 47 (6 ): 4239 -4256
[本文引用: 1]
[6]
He X Li J Lin Y et al .A domain decomposition method for the steady-state navier-stokes-darcy model with beavers-joseph interface condition
. Siam Journal on Scientific Computing , 2015 , 37 (5 ): S264 -S290
[本文引用: 1]
[7]
Neale G Nader W Practical significance of Brinkman’s extension of Darcy’s law: Coupled parallel flows within a channel and a bounding porous medium
.The Canadian Journal of Chemical Engineering , 1974 , 52 (4 ): 475 -478
[本文引用: 1]
[8]
Vafai K Thiyagaraja R Analysis of flow and heat transfer at the interface region of a porous medium
. International Journal of Heat and Mass Transfer , 1987 , 30 (7 ): 1391 -1405
[本文引用: 1]
[9]
Vafai K Kim SJ Fluid mechanics of the interface region between a porous medium and a fluid layer—an exact solution
.International Journal of Heat and Fluid Flow , 1990 , 11 (3 ): 254 -256
[本文引用: 1]
[10]
Ucar E Mobedi M Pop I Effect of an inserted porous layer located at a wall of a parallel plate channel on forced convection heat transfer
.Transport in Porous Media , 2013 , 98 (1 ): 35 -57
[本文引用: 5]
[11]
Shokouhmand H Jam F Salimpour MR The effect of porous insert position on the enhanced heat transfer in partially filled channels
.International Communications in Heat and Mass Transfer , 2011 , 38 (8 ): 1162 -1167
[本文引用: 1]
[12]
Cekmer O Mobedi M Ozerdem B et al .Fully developed forced convection in a parallel plate channel with a centered porous layer
.Transport in Porous Media , 2012 , 93 (1 ): 179 -201
[本文引用: 1]
[13]
Ochoa-Tapia JA Whitaker S Momentum transfer at the boundary between a porous medium and a homogeneous fluid—I. Theoretical development
.International Journal of Heat and Mass Transfer , 1995 , 38 (14 ): 2635 -2646
[本文引用: 3]
[14]
Whitaker S The Forchheimer equation: A theoretical development
.Transport in Porous media , 1996 , 25 (1 ): 27 -61
[本文引用: 1]
[15]
Ochoa-Tapia JA Whitaker S Momentum transfer at the boundary between a porous medium and a homogeneous fluid—II. Comparison with experiment
.International Journal of Heat and Mass Transfer , 1995 , 38 (14 ): 2647 -2655
[本文引用: 1]
[16]
Kuznetsov AV Analytical investigation of the fluid flow in the interface region between a porous medium and a clear fluid in channels partially filled with a porous medium
.Applied Scientific Research , 1996 , 56 (1 ): 53 -67
[本文引用: 2]
[17]
Tilton N Cortelezzi L The destabilizing effects of wall permeability in channel flows: A linear stability analysis
. Physics of Fluids (1994-present ), 2006 , 18 (5 ): 051702
[18]
Tilton N Cortelezzi L Linear stability analysis of pressure-driven flows in channels with porous walls
.Journal of Fluid Mechanics , 2008 , 604 : 411 -445
[19]
Li Q Lei HY Dai CS Linear stability of a fluid channel with a porous layer in the center
.Acta Mechanica Sinica , 2014 , 30 (1 ): 28 -36
[本文引用: 1]
[20]
Dai C Li Q Lei H Instability of Poiseuille flow in a channel filled with multilayer porous media
. Journal of Porous Media , 2015 , 18 (2 ): 165 -177
[本文引用: 1]
[21]
Whitaker S The forchheimer equation: A theoretical development
.Transport in Porous Media , 1996 , 25 (1 ): 27 -61
[本文引用: 1]
[22]
Das DB Nassehi V Wakeman RJ A finite volume model for the hydrodynamics of combined free and porous flow in sub-surface regions
.Advances in Environmental Research , 2002 , 7 (1 ):35 -58
[23]
Tan H Pillai KM Finite element implementation of stress-jump and stress-continuity conditions at porous-medium, clear-fluid interface
.Computers & Fluids 2009 , 38 (6 ):1118 -1131
[24]
Yu P Lee TS Zeng Y et al .A numerical method for flows in porous and homogenous fluid domains coupled at the interface by stress jump
.International Journal for Numerical Methods in Fluids , 2010 , 53 (11 ): 1755 -1775
[25]
王丽 . 部分填充多孔介质复合腔体内流体流动及传热传质的研究. [硕士论文]
. 济南:山东建筑大学 , 2010
(Wang Li Convective heat and Mass transfer in a complex cavity partially filled with porous medium. [Master Thesis]
. Jinan: Shandong Construction University , 2010 (in Chinese))
[26]
刘芳 . 多孔介质与流体空间交界面滑移效应及其影响机理. [博士论文]
. 济南:山东大学 , 2011
(Liu Fang The interfacial slip effect and its influencing mechanism between a porous medium and fluid region. [PhD Thesis]
. Jinan: Shandong University , 2011 (in Chinese))
[27]
戴传山 , 李琪 , 雷海燕 . 考虑非达西效应的多孔介质与自由流体多层泊松流求解问题
. 岩石力学与工程学报 , 2015 , 34 (s1 ): 3455 -3459
[本文引用: 2]
(Dai Chuanshan Li Qi Lei Haiyan Solution for the poiseuille flow in a fluid channel with a porous media insert by considering non-Darcy effects
.Chinese Journal of Rock Mechanics and Engineering 2015 , 34 (s1 ): 3455 -3459 (in Chinese))
[本文引用: 2]
[28]
Huang P Cai M Wang F A Newton type linearization based two grid method for coupling fluid flow with porous media flow
.Applied Numerical Mathematics , 2016 , 106 : 182 -198
[本文引用: 1]
[29]
Yadollahi-Farsani H Frakes D Herrmann M. Geometry based method for simulating fluid flow through heterogeneous porous media. US20170098019[P/OL]. 2017 -04-06
[本文引用: 1]
[30]
孟旭辉 , 王亮 , 郭照立 . 多孔介质中流固作用力的动量交换计算
. 力学学报 , 2014 , 46 (4 ): 525 -532
[本文引用: 1]
(Meng Xuhui Wang Liang Guo Zhaoli Forced evaluation using momentum-exchange method in porous media
.Chinese Journal of Theoretical and Applied Mechanics 2014 , 46 (4 ): 525 -532 (in Chinese))
[本文引用: 1]
[31]
Breugem WP The effective viscosity of a channel-type porous medium
.Physics of Fluids , 2007 , 19 (10 ): 103104
[32]
Givler RC Altobelli SA A determination of the effective viscosity for the Brinkman-Forchheimer flow model
.Journal of Fluid Mechanics , 1994 , 258 (258 ): 355 -370
[本文引用: 1]
[33]
Al-Azmi BS Analysis of transport models and computation algorithms for flow through porous media. [PhD Thesis]
. Ohio: The Ohio State University , 2003
[本文引用: 1]
[34]
Taylor GI A model for the boundary condition of a porous material. Part 1
.Journal of Fluid Mechanics , 1971 , 49 (2 ): 319 -326
[35]
Richardson S A model for the boundary condition of a porous material. Part 2
. Journal of Fluid Mechanics , 1971 , 49 (2 ): 327 -336
Boundary conditions at a naturally permeable wall
4
1967
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
... [1 ]的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
... 根据Beavers和Joseph [1 ] 提出的B-J速度滑移界面模型,有如下方程 ...
... 其中, α * ~ 4 ,主要受界面处多孔介质结构性质、雷诺数等的影响 [1 ] ,与应力跳跃系数 β [2,34-35 ] . 在多孔层内流体运动符合Darcy定律,即不考虑Brinkman项及Forchheimer项,方程(2)变为 ...
Slip and no-slip velocity boundary conditions at interface of porous, plain media
1
1992
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
Instability of Poiseuille flow in a fluid overlying a porous layer
1
2006
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
Coupled Stokes-Darcy model with Beavers-Joseph interface boundary condition
1
2010
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
Finite element approximations for stokes-darcy flow with beavers-joseph interface conditions
1
2010
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
A domain decomposition method for the steady-state navier-stokes-darcy model with beavers-joseph interface condition
1
2015
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
Practical significance of Brinkman’s extension of Darcy’s law: Coupled parallel flows within a channel and a bounding porous medium
1
1974
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
Analysis of flow and heat transfer at the interface region of a porous medium
1
1987
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
Fluid mechanics of the interface region between a porous medium and a fluid layer—an exact solution
1
1990
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
Effect of an inserted porous layer located at a wall of a parallel plate channel on forced convection heat transfer
5
2013
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
... 将本文所得解析解模型进行计算,并与文献[10 ]在相同工况下的解析结果进行对比,发现不考虑界面应力跳跃时,即多孔 介质--自由流界面采用速度及剪切应力均为连续模型时,文献[10 ]的解析结果与本文在跳跃系数 β = 0 图2 所示,文献[10 ]提出的解析解为本文所得结果模型的一个特例,证明了本文结果模 型的正确性. 而由前人研究可知 [16 ] ,在某些情况下,界面效应是不可忽略的,特别是界面处固体颗粒对流体动量的非连续影响,利 用本文给出的解析解模型可以更客观的描述考虑界面应力跳跃情况下的多孔介质--自由流耦合通道的流动特性, 从而拓宽及完善非对称多孔介质--自由流耦合通道内复杂界面流体流动特性解析解的应用条件. ...
... ]在相同工况下的解析结果进行对比,发现不考虑界面应力跳跃时,即多孔 介质--自由流界面采用速度及剪切应力均为连续模型时,文献[10 ]的解析结果与本文在跳跃系数 β = 0 图2 所示,文献[10 ]提出的解析解为本文所得结果模型的一个特例,证明了本文结果模 型的正确性. 而由前人研究可知 [16 ] ,在某些情况下,界面效应是不可忽略的,特别是界面处固体颗粒对流体动量的非连续影响,利 用本文给出的解析解模型可以更客观的描述考虑界面应力跳跃情况下的多孔介质--自由流耦合通道的流动特性, 从而拓宽及完善非对称多孔介质--自由流耦合通道内复杂界面流体流动特性解析解的应用条件. ...
... 所示,文献[10 ]提出的解析解为本文所得结果模型的一个特例,证明了本文结果模 型的正确性. 而由前人研究可知 [16 ] ,在某些情况下,界面效应是不可忽略的,特别是界面处固体颗粒对流体动量的非连续影响,利 用本文给出的解析解模型可以更客观的描述考虑界面应力跳跃情况下的多孔介质--自由流耦合通道的流动特性, 从而拓宽及完善非对称多孔介质--自由流耦合通道内复杂界面流体流动特性解析解的应用条件. ...
... 本文结果与文献[10 ]结果比较 ...
The effect of porous insert position on the enhanced heat transfer in partially filled channels
1
2011
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
Fully developed forced convection in a parallel plate channel with a centered porous layer
1
2012
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
Momentum transfer at the boundary between a porous medium and a homogeneous fluid—I. Theoretical development
3
1995
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
... [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
... 图12 所示为Da =0.01, γ = - 0.5 α * Y = γ Y = - 1.0 ) 均出现了速度不连续现象. α * U ̂ i α * ( Y = - 1.0 ) α * 图6 (a)进行比较,可以看出采用Brinkman-extended Darcy模型并结合Ochoa-Tapia和Whitaker [13 ] 提出的界面条件能够很好的解决B-J速度滑移条件下的速度不连续问题,不仅能够使与自由流体区接触界面处速度连续,也能保证与多孔介质接触的非渗透性固体壁面处速度为0,更符合实际现象. 另外,Ochoa-Tapia和Whitaker [13,15 ] 指出,在利用复杂体积平均方法推导界面模型时,Brinkman-extended Darcy模型与Stokes’方程的匹配过程要求同时保证应力不连续及速度连续. ...
The Forchheimer equation: A theoretical development
1
1996
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
Momentum transfer at the boundary between a porous medium and a homogeneous fluid—II. Comparison with experiment
1
1995
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
Analytical investigation of the fluid flow in the interface region between a porous medium and a clear fluid in channels partially filled with a porous medium
2
1996
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
... 将本文所得解析解模型进行计算,并与文献[10 ]在相同工况下的解析结果进行对比,发现不考虑界面应力跳跃时,即多孔 介质--自由流界面采用速度及剪切应力均为连续模型时,文献[10 ]的解析结果与本文在跳跃系数 β = 0 图2 所示,文献[10 ]提出的解析解为本文所得结果模型的一个特例,证明了本文结果模 型的正确性. 而由前人研究可知 [16 ] ,在某些情况下,界面效应是不可忽略的,特别是界面处固体颗粒对流体动量的非连续影响,利 用本文给出的解析解模型可以更客观的描述考虑界面应力跳跃情况下的多孔介质--自由流耦合通道的流动特性, 从而拓宽及完善非对称多孔介质--自由流耦合通道内复杂界面流体流动特性解析解的应用条件. ...
The destabilizing effects of wall permeability in channel flows: A linear stability analysis
2006
Linear stability analysis of pressure-driven flows in channels with porous walls
2008
Linear stability of a fluid channel with a porous layer in the center
1
2014
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
Instability of Poiseuille flow in a channel filled with multilayer porous media
1
2015
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
The forchheimer equation: A theoretical development
1
1996
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
A finite volume model for the hydrodynamics of combined free and porous flow in sub-surface regions
2002
Finite element implementation of stress-jump and stress-continuity conditions at porous-medium, clear-fluid interface
2009
A numerical method for flows in porous and homogenous fluid domains coupled at the interface by stress jump
2010
部分填充多孔介质复合腔体内流体流动及传热传质的研究. [硕士论文]
2010
部分填充多孔介质复合腔体内流体流动及传热传质的研究. [硕士论文]
2010
多孔介质与流体空间交界面滑移效应及其影响机理. [博士论文]
2011
多孔介质与流体空间交界面滑移效应及其影响机理. [博士论文]
2011
考虑非达西效应的多孔介质与自由流体多层泊松流求解问题
2
2015
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
... 对于渗透性更小的多孔介质层,即Da =10 - 5 时(图3 (c)),界面处的速度也会随 β Da =1.0及Da =0.01时的情况. 所不同的是,由于插入的较小渗透率多孔层,会更大程度地阻碍流体在其内的运动,会在距界面很小范围内就将流体速度制止,使流速基本趋于0,并在多孔介质内形成一个不随高度变化的很小的固定速度值,即Darcy速度,一般将界面位置到刚出现Darcy速 度时的通道高度 σ 27 ]给出的多孔介质分区模型相同, 如图3 (d)所示,而由于质量守恒,使自由流体区具有更大的流体速度. 此时改变界面应力系数 β Da =1.0及Da =0.01的多孔介质层而言较小,而Da =1.0的多孔层又小于Da =0.01的多孔介质层. 因此, γ Da 的多孔层,改变界面性质可明显控制多孔层及自由流体层内的流体速度分布. ...
考虑非达西效应的多孔介质与自由流体多层泊松流求解问题
2
2015
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
... 对于渗透性更小的多孔介质层,即Da =10 - 5 时(图3 (c)),界面处的速度也会随 β Da =1.0及Da =0.01时的情况. 所不同的是,由于插入的较小渗透率多孔层,会更大程度地阻碍流体在其内的运动,会在距界面很小范围内就将流体速度制止,使流速基本趋于0,并在多孔介质内形成一个不随高度变化的很小的固定速度值,即Darcy速度,一般将界面位置到刚出现Darcy速 度时的通道高度 σ 27 ]给出的多孔介质分区模型相同, 如图3 (d)所示,而由于质量守恒,使自由流体区具有更大的流体速度. 此时改变界面应力系数 β Da =1.0及Da =0.01的多孔介质层而言较小,而Da =1.0的多孔层又小于Da =0.01的多孔介质层. 因此, γ Da 的多孔层,改变界面性质可明显控制多孔层及自由流体层内的流体速度分布. ...
A Newton type linearization based two grid method for coupling fluid flow with porous media flow
1
2016
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
-04-06
1
2017
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
多孔介质中流固作用力的动量交换计算
1
2014
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
多孔介质中流固作用力的动量交换计算
1
2014
... 由于多孔介质与流体之间存在着复杂界面结构,一直以来有关多孔介质内的流动模型、以及多孔介质与自由流体间、多孔介质与无滑移固定界面间的边界条件处理是许多研究者关注的对象. Beavers和Joseph [1 ] 首次提出采用滑移速度处理多孔介质与自由流体接触的界面条件问题,简称B-J模型,认为可以通过这种滑移现象来近似解释界面附近边界层对外流的影响. Sahraoui和Kavian [2 ] 指出滑移速度系数的值依赖于界面上流体的流动方向、雷诺数、流体区范围及表面固体材料排列无规则情况. Chang等 [3 ] 在多孔介质内部采用Darcy模型以及在自由流体层与多孔介质层界面处采用B-J模型,研究了二维通道中流体覆盖多孔介质层结构的Poiseuille流问题. 然而多孔介质中采用的Darcy模型不能解决边界问题,会造成界面处速度的不连续. Cao等 [4 ] 研究结果表明,有限元法对B-J条件耦合的Darcy流与自由流的研究有良好的适用性,并进一步用此方法研究了地下水的流动问题 [5 ] . He等 [6 ] 同样采用Darcy模型及B-J界面条件,用非奇异解的一个分支分析了此模型的适用性. 之后Neale和Nader [7 ] 提出了Brinkman-extended Darcy模型,Vafai和Thiyagaraja [8 ] 以及Vafai和Kim [9 ] 将此模型应用到多孔介质层中,以保证速度和剪切力在界面处连续. Ucar等 [10 ] 采用速度、应力均连续界面条件对非对称通道内部分填充多孔层的流动与传热给出了解析解. Shokouhmand等 [11 ] 和Cekmer等 [12 ] 也同样采用Brinkman-extended Darcy模型并结合速度、应力均连续界面条件对复合多孔介质对称通道内的流动与传热给问题出了数值解或解析解. 之后,Ochoa-Tapia和Whitaker [13 ] 提出了一种新模型,认为在界面处速度是连续的但剪切力不连续,并且Whitaker [14 ] 进一步用复杂的体积平均法通过N-S方程推得了考虑惯性项时多孔介质内满足的方程,从而使多孔介质内部流动方程更加完善. Ochoa-Tapia和Whitaker [15 ] 进一步得出应力跳跃系数取值范围为[-1,1.5],且在此范围内对此系数作调整时,所得结果与Beavers和Joseph [1 ] 的结果符合良好. 之后,该应力跳跃条件被许多研究者所应用. Kuznestsov [16 ] 采用应力跳跃条件对部分填充多孔介质的中心对称平行板和圆柱形通道内的流体流动进行了研究,给出了界面处流体速度的解析解,并指出界面应力跳跃的重要性. Tilton和Cortelezzi [17-18 ] ,Li等 [19 ] , Dai等 [20 ] 均采用Ochoa-Tapia和Whitaker [13 ] 提出的界面方程并使用Whitaker [21 ] 提出的多孔介质模型,对不同含有多孔介质层通道结构中的压力驱动流进行了相关流动稳定性的研究,但均研究的是对称通道,具有中心处边界条件,没有进一步给出应力系数与界面速度及流体摩擦系数的解析关系. 另外,文献[22-26]也都采用应力跳跃条件及有限容积法或有限元法等多种数值方法研究了部分填充多孔层通道内的平行流动或斜向流动或双扩散自然对流问题. 戴传山等[27 ] 提出将多孔介质层分为核心区域与边界影响区,给出了考虑界面非线性跳跃条件下的渗流速度场的数值解方法. Huang等[28 ] 和Yadollahi-Farsani等[29 ] 又分别提出基于牛顿型线性化两网格方法及几何结构的方法研究复杂多孔介质流. 孟旭辉等[30 ] 采用格子波尔兹曼数值方法分析了流体流经多孔介质时两者的动量交换过程并提出一种高效的动量交换法来计算流固作用力. ...
The effective viscosity of a channel-type porous medium
2007
A determination of the effective viscosity for the Brinkman-Forchheimer flow model
1
1994
... 其中, β [ - 1,1.5 ] [13,15 ] ,是与多孔介质孔隙率、渗透率和孔径 等多种因素密切相关的界面动量分配系数,需通过实验进行确定. 当 β = 0 u i G = - ∂ p ∂ x U = μ f uG H 2 M = μ e ff μ f Da = k H 2 R = 1 MDa . 其中,较多学者在应用Brinkman-extended Darcy模型时认为 μ e ff = μ f [32 ] 通过实验研究指出在某些情况下区分这两个参数是十分重要的,并建议 μ e ff = ( 7 . 5 - 2.4 + 3.4 ) μ f . Ochoa-Tapia和Whitaker [13,15 ] 在研究复合通道多孔介质流时则采用关系式 μ e ff = μ f / ε ε [33 ] 研究发现当 μ e ff / μ f ~ 7.5 范围内变化时,对复合通道内流体的速度分布影响较小. 因此,本文将暂不考虑 M μ e ff = μ f / ε μ e ff ε = 0.6 M = 1 / 0.6 . 将上述流体运动控制方程(1) ~ (5) 改写成无量纲形式,可得自由流体区与多孔介质区内流体无量纲运动方程分别为 ...
Analysis of transport models and computation algorithms for flow through porous media. [PhD Thesis]
1
2003
... 其中, β [ - 1,1.5 ] [13,15 ] ,是与多孔介质孔隙率、渗透率和孔径 等多种因素密切相关的界面动量分配系数,需通过实验进行确定. 当 β = 0 u i G = - ∂ p ∂ x U = μ f uG H 2 M = μ e ff μ f Da = k H 2 R = 1 MDa . 其中,较多学者在应用Brinkman-extended Darcy模型时认为 μ e ff = μ f [32 ] 通过实验研究指出在某些情况下区分这两个参数是十分重要的,并建议 μ e ff = ( 7 . 5 - 2.4 + 3.4 ) μ f . Ochoa-Tapia和Whitaker [13,15 ] 在研究复合通道多孔介质流时则采用关系式 μ e ff = μ f / ε ε [33 ] 研究发现当 μ e ff / μ f ~ 7.5 范围内变化时,对复合通道内流体的速度分布影响较小. 因此,本文将暂不考虑 M μ e ff = μ f / ε μ e ff ε = 0.6 M = 1 / 0.6 . 将上述流体运动控制方程(1) ~ (5) 改写成无量纲形式,可得自由流体区与多孔介质区内流体无量纲运动方程分别为 ...
A model for the boundary condition of a porous material. Part 1
1971
A model for the boundary condition of a porous material. Part 2
1971