引 言
稳定和不稳定流形是非线性动力系统的重要几何结构,是研究动力系统全局动态特性的重要工具 [1 ] . 稳定和不稳定流形的计算在动力系统分析和控制系统设计等领域有重要应用 [2-7 ] ,例如非线性系统稳定平衡点的稳定域的边界可由边界上不稳定平衡点的稳定流形获得 [8-11 ] . 不稳定流形可看作稳定流形的时间反向,因此本文重点研究稳定流形的情形.
一般系统的全局稳定流形无法得到解析表达式,并且稳定流形无法通过隐式方法计算 [12 ] . 稳定流形定理 [13-14 ] 表明,系统的稳定流形与其线性化系统的稳定特征子空间在平衡点处相切. 因此可以由稳定特征子空间上平衡点的邻域出发,通过迭代计算系统的稳定流形. 最直接的迭代方法是简单积分法,即以稳定特征子空间上的一个椭圆作为稳定流形的初始估计 M 0 M 0 Δ t Δ s M 1 M i M i + 1 M i + 1 M i + 1 M i
为克服简单积分法的局限性,一些适用性较强的算法被相继提出. 轨道弧长算法 [15 ] 将向量场各方向的生长速度归一化,使得轨道沿各方向同速生长. 然而轨道的生长仍然受制于系统向量场,相邻的初始点也可能产生较大的分离. 测地水平集算法 [16-17 ] 通过在 M i M i + 1 M i + 1 M i [18-19 ] 可以较容易地确定流形的轮廓,但该 算法无法反映出流形的增长趋势. 边值问题(BVP)连续算法 [20 ] 基于微分方程解的连续性,利用轨道扫描出流形面,因此该算法将在近平衡点处产生大量的点,需要对计算结果进行相应的后期处理. 偏微分方程(偏微分方程)算法 [21 ] 借鉴前沿推进网格生成算法 [22-23 ] ,该算法对流形网格具有较好的控制能力,计算效率较高. 此外还有扩展轨迹算法 [24 ] ,参数化算法等 [25-28 ] . 国内方面,两步法 [29 ] 的第一步通过求解初值问题快速确定流形上点的位置,第二步则利用第一步计算出的点勾画流形的图像. 自适应因子轨道延拓算法 [30 ] 根据计算的精度要求自适应的调整轨道的数目,以保证轨道间距小于误差限. 该算法中轨道上的点是等间距的. 误差限和轨道点间距都是全局统一的,没有根据流形曲率进行调整. 径向增长控制算法 [31 ] 通过引入径向控制因子将原始动力学系统进行归一化,使得各方向的轨道生长速度相同. 异构算法 [32-33 ] 利用相邻的取样轨道连接形成三角形构成局部流形,但其取样轨道间的距离限制和轨道点间距也是全局 统一的,没有根据流形曲率进行调整.
可见这些算法的共同点是:流形是从平衡点附近逐渐生长出来的. 根据流形生长方式的不同,可以将这些算法分为两类:一类是利用系统 的轨道生成流形网格,如轨道弧长算法、边值问题连续算法、扩展轨迹算法、两步法、自适应因子轨道延拓算法、径向增长控制算法、异构算法等. 这类算法的优点是可以利用成熟的数值积分算法求解系统的轨道,并且每段轨道可以构建出流形网格的多个单元. 其缺点是不便于利用流形本身的几何特征调整计算过程. 另一类算法则不利用轨道构建网格,而是直接生长出流形网格的单元,如测地水平集算法和偏微分方程算法. 这类算法的优点是流形生长过程不受系统向量场影响,并且对流形网格具有较强的控制能力. 其缺点是无法直接给出系统的轨道.
另一方面,现有算法未能充分利用流形的曲率信息对计算过程进行动态调整,流形单元的基准尺寸是全局统一的. 然而一般系统的流形曲率在全局范围内可能有较大的变化,全局统一的单元尺寸无法适应流形各部分的特点. 例如洛伦兹流形,随着计算面积的增大,流形的一部分将变得越来越卷曲,这意味着其曲率逐渐增大,而流形另一部分则比较平坦. 在曲率较大的部分应采用更小尺寸的单元才能得到较为准确的结果,而在曲率较小的部分则可以使用较大尺寸的单元以减小计算量. 可见单元尺寸的全局自适应对于提高稳定流形的计算质量是十分必要的.
为适应稳定流形曲率在全局范围内的变化,本文将设计一种能根据流形的曲率对流形网格尺寸进行动态调整的算法. 考虑到偏微分 方程算法对流形网格具有较强的控制能力,且便于利用流形的曲率信息. 因此本文将在偏微分方程算法的基础上提一种二维稳定流形自适应推进算法. 本工作采用自适应推进算法,研究了二维不变流形 的计算问题,以期为动力系统分析及控制系统稳定性分析提供参考.
1 稳定和不稳定流形
对于由常微分方程组所描述的系统
x = f ( x ) ( 1 )
其中, x ∈ R n f : R n → R n x 0 f ( x 0 ) = 0 x 0 W s ( x 0 ) W u ( x 0 )
$$ \left. \bal W^{\rm s} ({\pmb x}_0 ) = \{{\pmb x} \in {\bf R} ^n\vert \mathop {\lim}\limits_{t \to \infty } \phi (t,{\pmb x}_0 ) = {\pmb x}_0 \} \\ W^{\rm u} ({\pmb x}_0 ) = \{{\pmb x} \in {\bf R}^n\vert \mathop {\lim}\limits_{t \to \infty } \phi ( - t,{\pmb x}_0 ) = {\pmb x}_0 \} \end{array} \right\} (2) $$
其中, ϕ ( t , x 0 ) x 0 x = - f ( x )
系统(1)对应于 x 0 f ( x ) x 0 D f ( x 0 ) = ∂ f / ∂ x e 1 , e 2 D f ( x 0 ) E s ( x 0 ) e 1 , e 2 E s ( x 0 ) = S pan ( e 1 , e 2 ) . 稳定流形定理指出,在 x 0 W s ( x 0 ) E s ( x 0 ) [13-14 ] . 因此可以将 E s ( x 0 ) x 0 W s ( x 0 ) W s ( x 0 )
二维稳定流形自适应推进算法正是从 E s ( x 0 )
2 二维稳定流形自适应推进算法
自适应推进算法的基本思路是:首先确定稳定特征子空间中平衡点的一个邻域,并生成一层围绕该邻域的初始备选点和备选网格,根据相切条件更新备选点的坐标. 将距离平衡点最近的备选点接受为稳定流形网格的已知点,并根据稳定流形的曲率自适应地扩展出新的备选网格单元(三角形单元). 通过持续的网格扩展逐渐计算出更大面积的稳定流形. 该算法的主要步骤为:
步骤1 利用稳定特征子空间计算初始邻域,生成初始备选点和备选网格.
步骤2 根据相切条件更新备选点的坐标,并估计备选点与平衡点之间的轨道长度.
步骤3 将到平衡点轨道长度最短的备选点 v ̅
步骤4 根据稳定流形的曲率自适应地扩展出新的备选网格单元.
步骤5 更新 v ̅
步骤6 若到平衡点的轨道长度 Σ
2.1 初始邻域和初始备选网格
根据稳定流形定理 [13-14 ] ,系统稳定特征子空间中 x 0 e 1 , e 2 D f ( x 0 ) e 1 , e 2
$$
\left.\!\!\begin{array}{l}
{\pmb q}_1 = {\pmb e}_1 / \left\| {{\pmb e}_1 } \right\| \\\\
{\pmb q}_2 = {\pmb e}_2 - \dfrac{({\pmb e}_2 ,{\pmb
q}_1 )}{({\pmb q}_1 ,{\pmb q}_1 )}{\pmb q}_1 \Bigg / \left\| {{\pmb e}_2 - \dfrac{({\pmb e}_2 ,{\pmb q}_1
)}{({\pmb q}_1 ,{\pmb q}_1 )}{\pmb q}_1 } \right\|
\end{array}\!\! \right\} (3)
$$
由式(3)可知 q 1 , q 2 e 1 , e 2 q 1 , q 2 q 1 , q 2
p ( i ) = [ q 1 sin ( 2 i / N ) + q 2 cos ( 2 i / N ) ] R + x 0 ( 4 )
其中, i = 1,2 , ⋯ , N N R R x 0 R . 具体地说就是先计算出 x 0 R R x 0 R N Δ 0 N = 2 R / Δ 0 Δ 0 # x 2264 ; R .
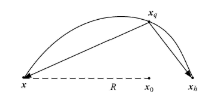
若 e 1 , e 2 e 1 , e 2 x 0 e 1,2 = u ± i v α ± i β . 如图1 所示,由点 x = x 0 + R u / u Δ t = / ( 2 β ) x q = ϕ ( Δ t , x ) x h = ϕ ( 2 Δ t , x ) . 于是可以得到平行于系统稳定特征子空间的向量 x q x x q x h . 对 x q x x q x h
图1 根据轨道确定稳定特征子空间示意图
Fig. 1 Schematic of determination of stable eigenspaces based on trajectory
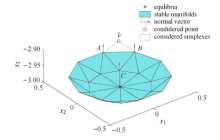
如图2 所示,初始邻域的前沿点和平衡点构成的三角形单元给出了初始的稳定流形网格. 稳定流形的剩余部 分则是从这个初始估计逐渐生长出来. 连接相邻的前沿点构成稳定流形的前沿,基于前沿上的每个线段产生备选点和备选网格. 初始备选点位于系统的稳定特征子空间中. 备选点与对应的前沿边相连构成备选三角单元,全体备选三角单元构成备选网格. 初始备选单元为等边三角形,在图2 的示意中 R = 0.3 Δ 0 = 0.2 .
图2 初始邻域和初始备选网格示意图
Fig. 2 Schematic of initial neighborhood and initial considered mesh
2.2 相切条件
稳定流形曲面并非事先已知的,因此在对其进行网格剖分时,需要先计算出稳定流形上点的坐标,这可以通过相切条件实现. 对于 R 3 W s ( x 0 ) x = ( x 1 , x 2 , x 3 )
g ( x 1 , x 2 ) - x 3 = 0 ( 5 )
则 W s ( x 0 ) g ( x 1 , x 2 ) - x 3 = 0 x [21 ]
$$f(x_1 ,x_2 ,g(x_1 ,x_2 )) \left[\!\! \begin{array}{ccc} {\dfrac{\partial g}{\partial x_1 }} & {\dfrac{\partial g}{\partial x_2}} & { - 1}\end{array} \!\! \right]^{\rm T}=0 (6)$$
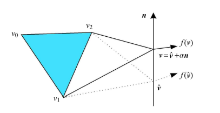
解方程(6)即可得到稳定流形的局部描述 g ( x 1 , x 2 ) . 由于方程(6)具有明显的几何意义,因此可以采用几何解法. 方程(6)的几何含 义为在 x g ( x 1 , x 2 ) - x 3 = 0 x g ( x 1 , x 2 ) - x 3 = 0 g ( x 1 , x 2 ) - x 3 = 0 v 1 v 2 v v 1 , v 2 , v ∈ R 3 . 如图3 所示,该三角形的两个顶点 v 1 v 2 v 0 v 1 v 2 v
图3 相切条件的几何解释
Fig. 3 Geometric explanation of the tangent condition
为计算顶点 v v 0 v 1 v 2 v v v 0 v 1 v 2 v 0 v 1 v 2 v 1 v 2 v ̂ v 1 v 2 v ̂ n f ( v ̂ ) v v = v . 然而,通常 v v v 1 v 2 v ̂ v = v + α n
$${\pmb n}^{\rm T}f(\hat{\pmb v} + \alpha {\pmb n}) = 0 (7)$$
则三角形 v 1 v 2 v v v . 可见问题最终转化为求解方程(7)中的未知数 α . 另外,为保证算法的稳定性和精度,点 v [34 ] 才能被接受为已知点 [21 ] .
由相切条件的几何解释可知,只要备选三角单元的尺寸选择的合适,则备选点的初始坐标与其最终被接受的坐标相差很小. 网格单元的长宽比是衡量流形网格质量的重要指标. 对于三角形网格,网格单元越接近正三角形,则网格质量越高. 此外,网格单元尺寸对流形曲率的适应性也是衡量网格质量的重要方面. 网格单元尺寸对流形曲率的自适应性越好,则流形计算结果越准确,网格的质量也就越高. 可见稳定流形网格的质量可以由备选三角单元的生成规则控制的. 本文重点考虑网格单元尺寸对流形曲率的自适应性. 所提的自适应推进算法正是根据稳定流形的曲率特征自适应地生成备选三角单元,从而实现稳定流形网格的自适应推进.
2.3 单元尺寸自适应
根据相切条件,可以在稳定流形的前沿得到一个新的三角单元作为局部估计,并且估计的误差阶数为 O ( Δ 2 ) Δ [21 ] . 当稳定流形某部分卷曲程度高于其他部分时,就要求相应的估计误差小于其他部分. 因此必须根据稳定流形的曲率来自适应的调整三角单元的尺寸. 在估计离散曲率的诸多算法中 [35-37 ] ,Meyer 的方法几何意义简明且便于三角网格实现,因此本文采用Meyer方法来估计稳定流形的平均曲率 [38 ] .
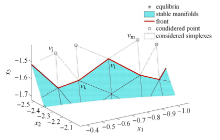
如图4 所示,设稳定流形在 A , B , C h A , h B , h C AB AB v ̂ Δ AB v ̂
$$\varDelta _{AB\hat {v}} = \dfrac{2h_C + \varepsilon }{ h_A + h_B + \varepsilon}\varDelta _{ABC} (8)$$
其中, Δ ABC ABC ε ε AB 2 Δ AB v ̂ AB v ̂ . 在实际的编程实现中,应对单元尺寸自适应设定限制,如限制 Δ AB v ̂ 2 Δ ABC
图4 网格单元尺寸自适应示意图
Fig. 4 Adaptability of mesh simplex size
单元尺寸自适应的引入提高了算法对流形曲率变化的适应性,同时也对算法的性能带来了影响. 在迭代误差方面,若流形曲率持续减小,则网格单元尺寸会随之增大,迭代误差相应地增大,计算精度随之下降. 因此为保证算法的全局精度,应设置单元尺寸的上限(本文中设置为初始尺寸的二倍). 偏微分方程算法的全局误差阶数为 O ( Δ ) [21 ] ,设置网格单元尺寸上限后,本文算法也可获得全局一阶精度. 在计算量方面,如果流形曲率急剧增大,则本算法使用的网格单元的尺寸就会急剧减小,为计算至指定轨线长度,所需的网格单元数将显著增多,计算量也将随之急剧增加. 实际编程实现中,可以通过设置单元尺寸的下限来防止计算量的急剧增加. 在计算速度方面,由于单元尺寸自适应本身需要额外的计算时间,并且单元尺寸的减小会增加计算网格数,因此本算法的计算速度比偏微分方程算法慢.
2.4 自适应推进
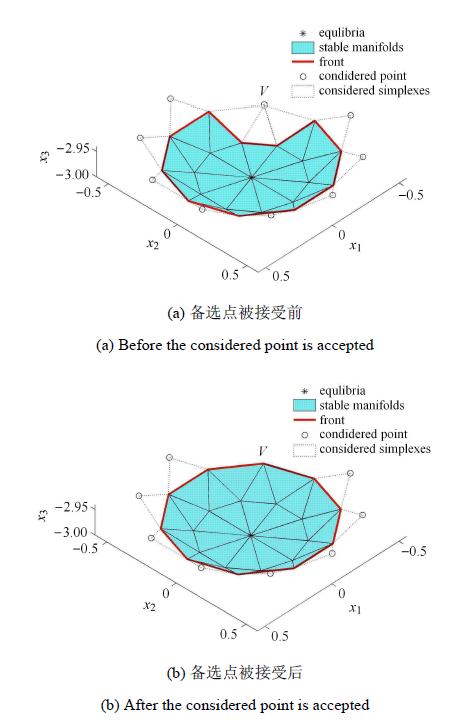
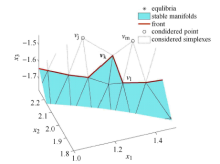
当有备选点被接受为已知点时,就意味着稳定流形网格向前推进了至少一个三角单元. 图5 (a)中,当 V 图5 (b)所示. 在更新后的前沿中将出现没有对应备选点的线段. 因此需要产生新的备选点和备选三角形为后续的推进做准备.
5 接受备选点与更新前沿
Fig. 5 Accepting considered points and updating front
如图5 所示,由于此时稳定流形网格的前沿已经发生了变化,需要根据前沿线段局部的几何特点自适应地放置新备选点. 一方面, 新放置的备选点及备选三角形要避免与已有网格交叠;另一方面,新的备选三角形的尺寸应适应稳定流形的曲率变化. 前者需要考虑 V V
设 v k v l v k v l v i v k v l v k v l = L . 现考虑为 v k v l v k v l v j v k v l v m v k v l v j v k v l v m v l v m v m v l v m γ 1 = ∠ v j v k v l v j v k v k v l γ 2 = ∠ v k v l v m v k v l v k v m γ = min ( γ 1 , γ 2 ) . 根据 γ
情形1 v k v l 图6 所示,以 v k v l v ̂ v k v ̂ = v l v ̂ = L 1 L # x 2264 ; Δ v k v l v ̂ / 2
$$ L_1 = \left\{ \!\! \begin{array}{ll} {2L\,,} & {L \leqslant 0.5\varDelta _{v_{\rm k} v_{\rm l} v} } \\\\ {\varDelta _{v_{\rm k} v_{\rm l} v} \,,} & {0.5\varDelta _{v_{\rm k} v_{\rm l} \end{array} \!\! \right. (9) $$
式(9)中的常数是经验性的,借鉴了曲面三角化中网格单元控制的经验方法 [22-23 ] . 式(9)中当 L 1 = 2 L v k v l > 1.8 Δ v k v l v ̂ v k v l γ ≥ π / 2
图6 γ ≥ π / 2
Fig. 6 Sketch map of new alternative triangle generation when γ < π / 2
情形2 γ = ∠ v k v l v m v k v m < 2 Δ v k v l v ̂ . 如图7 所示,若 v = v m v k v l v m v k v l . 若 v k v l v ̂ γ < π / 2 γ < π / 2
图7 ς = 10
Fig. 7 Sketch map of new alternative triangle generation when β = 8 / 3
3 算例应用
3.1 洛伦兹流形
洛伦兹系统 [39 ] 是验证稳定流形算法的经典算例,其方程为
$$ \left. \begin{array}{l} {\dot {x}_1 = \varsigma (x_2 - x_1 )} \\ {\dot {x}_2 = \rho x_1 - x_2 - x_1 x_3 } \\ {\dot {x}_3 = - \beta x_3 + x_1 x_2 } \end{array} \right\} (10) $$
其中, ρ = 28 λ ≈ - 2.67 , - 22.8 , 11.8 R = 2 .
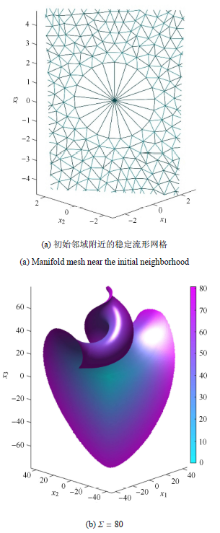
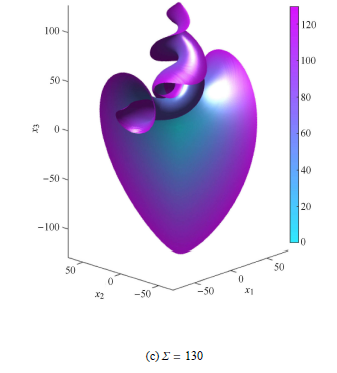
原点是系统的一个平衡点,其对应的雅可比矩阵特征值为 Δ 0 = 0.6 . 因此原点有二维稳定流形,该流形沿著名的蝶形吸引子向内螺旋. 在向内螺旋的过程中,稳定流形的曲率逐渐增大. 按本文的自适应推进算法,在洛伦兹流形的螺旋部分,网格三角单元的尺寸将逐渐减小以适应曲率的变化.
通过对原点附近稳定轨道的观察,选取初始邻域半径 Σ = 130 x ̇ 1 = ( p ( r , x 3 ) + x 3 ) x 1 2 mm ] x ̇ 2 = ( p ( r , x 3 ) + x 3 ) x 2 2 mm ] x ̇ 3 = p ( r , x 3 ) x 3 - x 1 2 - x 2 2 ( 11 ) . 计算至轨道长度 p ( r , x 3 ) = ( r - 3 ) [ ( r - 2 ) ( r + x 3 ) + 1.5 ] 图8 所示.
由图8 可知,利用本文所提算法计算稳定流形,所得流形网格在各方向上的推进速度大致是均衡的,不受系统向量场影响. 径向因子法 [31 ] 通过引入径向控制因子也能得到各项均衡发育的流形. 不同之处在于:径向因子法的主要目的是控制流形的径向增长速度,使得流形的发育在径向上是均衡的,而不关注流形网格单元尺寸对流形曲率的适应性;而本文算法的主要目的是让流形网格单元尺寸在全局范围根据流形曲率自适应地变化. 本文算法没有严格控制流形的径向生长速度,而是在算法步骤3中,选择距平衡点最近的流形备选点作为新的流形生长点,来大致平衡流形在各方向的生长发育. 在迭代的过程中,径向因子法实现了流形边缘到平衡点的径向距离相等,而本文算法则是使得流形前沿到平衡点的轨道长度相等.
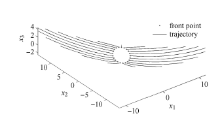
图9 是原点附近不同方向上的初始点的解轨道,各轨道的演化时间相同,但各轨道段的长度差异显著. 这表明洛伦兹系统向量场在不同方 向上的演化速度有较大差异. 而图8 的计算过程表明,稳定流形网格的扩展在各方向上是一致的,这表明算法不受系统向量场在各方向上演化速度差异的影响.
图8 洛伦兹流形的计算过程
Fig. 8 The computational process of Lorentz manifolds
图8-1 洛伦兹流形的计算过程(续)
Fig. 8-1 The computational process of Lorentz manifolds (continued)
图9 向量场在不同方向上演化速度的差异
Fig. 9 The difference of the evolution velocity of vector field in different directions
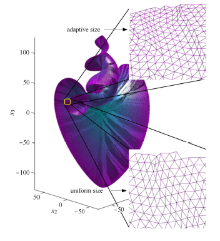
图10 是本文所提算法与偏微分方程算法在网格单元尺寸方面的对比. 可见随着洛伦兹流形的螺旋部分曲率的增大,利用本文 所提算法,网格三角 单元的尺寸自适应地逐渐减小. 而偏微分方程算法计算的网格单元尺寸无明显变化,仍然使用全局统一的单元尺寸. 洛伦兹流形的螺旋部分持续向内部卷曲,当螺旋半径接近全局统一尺寸时,偏微分方程算法将失效. 由于本文所提算法能根据流形曲率自适应地调整单元尺寸,因此可以持续有效地计算下去. 图10 的结果充分表明了所提算法对流形曲率变化的自适应性.
图10 所提算法与偏微分方程算法网格对比
Fig. 10 Mesh comparison between the proposed algorithm and the PDE approach
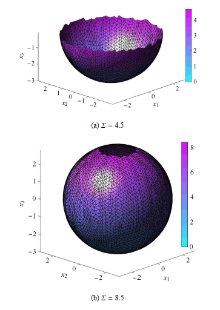
3.2 类球面流形
考虑如下系统 [40 ]
$$\left. \begin{array}{l} {\dot {x}_1 = (p(r,x_3 ) + x_3 )x_1 } \[2mm] {\dot {x}_2 = (p(r,x_3 ) + x_3 )x_2 } \[2mm] {\dot {x}_3 = p(r,x_3 )x_3 - x_1^2 - x_2^2 }\end{array} \right\} (11)$$
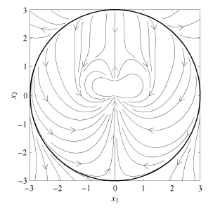
其中, x 3 x a = ( 0,0 , - 3 ) . 该系统在 x b = ( 0,0 , 1.5 ) x c = ( 0,0 , 0.5 ) x d = ( 0,0 , 3 ) x a λ = - 3 , - 3 , 4.5 . 其中 x a x 1 x 3 x a x 3 图11 所示, R = 0.3 图11 中的黑色曲线绕 Δ 0 = 0.2
通过对原点附近稳定轨道的观察,选取初始邻域半径 Σ = 8.5 x 1 x 3 x 1 x 3 图12 所示. 系统(11)的稳定流形的曲率在全局范围内变化不大,使用本文的自适应推进算法时网格单元 的尺寸不会有明显变化,这与图12 的计算结果是一致的.
图11 系统(11)在{Invalid MML}平面内的相图
Fig. 11 The phase portrait in the {Invalid MML} plane of the system (11)
图12 类球面流形的计算过程
Fig. 12 Computational process of sphere-like manifolds
4 结 论
本文提出了一种二维稳定流形的自适应推进算法,该算法相对于现有算法的改进之处在于,计算过程中算法能根据稳定流形的曲率自 适应的调整计算网格单元的尺寸. 这也是该算法相对于现有算法的最大优势. 这一改进使得该算法能持续有效地计算全局流形,并产生高质量的流形结果. 在洛伦兹流形计算中本文所提算法与偏微分方程算法进行了对比,结果表明了所提算法的自适应性.
(1)该算法对流形曲率具有全局自适应性,能根据稳定流形的曲率自适应地调整网格计算单元的尺寸,因而能持续有效的计算全局稳定流形.
(2)该算法中备选点的生成规则是由稳定流形的几何特征决定的,能充分利用流形曲率等几何特征,因此流形网格的扩展不受系统向量场在各方向上演化速度差异的影响.
后续将利用并行计算技术将所提算法并行化,进一步提高算法的计算效率.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
Guckenheimer J Krauskopf B Osinga HM et al .Invariant manifolds and global bifurcations
.Chaos: An Interdisciplinary Journal of Nonlinear Science , 2015 , 25 (9 ): 097604
[本文引用: 1]
[2]
贾蒙 . 高维非线性映射系统的不稳定流形计算方法研究
. 振动与冲击 , 2017 , 36 (17 ): 262 -266
(Jia Meng Computation method for unstable manifold of hénon map
.Journal of Vibration and Shock 2017 , 36 (17 ): 262 -266 (in Chinese))
[3]
郑丹丹 , 罗建军 , 张仁勇 等 . 基于混合Lie算子辛算法的不变流形计算
. 力学学报 , 2017 , 49 (5 ): 1126 -1134
(Zheng Dandan Luo Jianjun Zheng Renyong et al .Computation of invariant manifold based on symplectic algorithm of mixed Lie operator
.Chinese Journal of Theoretical and Applied Mechanics 2017 , 49 (5 ): 1126 -1134 (in Chinese))
[4]
Qu L Li YH Xu HJ et al .Aircraft nonlinear stability analysis and multidimensional stability region estimation under icing conditions
.Chinese Journal of Aeronautics , 2017 , 30 (3 ): 976 -982
[5]
贾建华 , 吕敬 , 王琪 . 带脉冲的三维引力辅助变轨研究
. 力学学报 , 2016 , 48 (2 ): 437 -446
(Jia Jianhua Lü Jing Wang Qi Powered gravity assist in three dimensions
.Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (2 ): 437 -446 (in Chinese))
[6]
李渊 , 邓子辰 , 叶学华 等 . 基于辛理论的载流碳纳米管能带分析
. 力学学报 , 2016 , 48 (1 ): 135 -139
(Li Yuan Deng Zichen Ye Xuehua et al .Analysing the wave scattering in single-walled carbon nanotube conveying fluid based on the symplectic theory
.Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (1 ): 135 -139 (in Chinese))
[7]
钱霙婧 , 翟冠峤 , 张伟 . 基于多项式约束的三角平动点平面周期轨道设计方法
. 力学学报 , 2017 , 49 (1 ): 154 -164
(Qian Yingjing Zhai Guanqiao ZhangWei. Planar periodic orbit construction around the triangular libration points based on polynomial constraints
.Chinese Journal of Theoretical and Applied Mechanics 2017 , 49 (1 ): 154 -164 (in Chinese))
[8]
Wang T Chiang HD On the number of unstable equilibrium points on spatially-periodic stability boundary
.IEEE Transactions on Automatic Control , 2016 , 61 (9 ): 2553 -2558
[9]
袁国强 , 李颖晖 . 积冰对飞机本体纵向非线性动力学稳定域的影响
. 西安交通大学学报 , 2017 , 51 (9 ): 153 -158
(Yuan Guoqiang Li Yinghui Effect of ice accretion on aircraft longitudinal nonlinear dynamical stability region
.Journal of Xi’an Jiaotong University 2017 , 51 (9 ): 153 -158 (in Chinese))
[10]
Chiang HD Wang T On the number and types of unstable equilibria in nonlinear dynamical systems with uniformly-bounded stability regions
.IEEE Transactions on Automatic Control , 2016 , 61 (2 ): 485 -490
[11]
Alberto LFC Chiang HD Characterization of stability region for general autonomous nonlinear dynamical systems
.IEEE Transactions on Automatic Control , 2012 , 57 (6 ): 1564 -1569
[12]
Krauskopf B Osinga HM Doedel EJ et al .A survey of methods for computing (un)stable manifolds of vector fields
.International Journal of Bifurcation and Chaos , 2005 , 15 (3 ): 763 -791
[本文引用: 1]
[13]
Kuznetsov YA Elements of Applied Bifurcation Theory. 2nd ed
. NY: Springer Verlag , 1998
[14]
Guckenheimer PJ Holmes. Nonlinear oscillations, dynamical systems and bifurcations of vector fields. 2nd ed. NY:
Springer-Verlag , 1986
[15]
Johnson ME Jolly MS Kevrekidis IG Two-dimensional invariant manifolds and global bifurcations: Some approximation and visualization studies
.Numerical Algorithms , 1997 , 14 (1 ): 125 -140
[本文引用: 1]
[16]
Krauskopf B Osinga HM Computing geodesic level sets on global (un)stable manifolds of vector fields
.SIAM Journal on Applied Dynamical Systems , 2003 , 2 (4 ): 546 -569
[17]
Guckenheimer J Worfolk P Dynamical systems: Some computational problems
. Dordrecht: Springer Netherlands , 1993
[18]
Dellnitz M Hohmann A A subdivision algorithm for the computation of unstable manifolds and global attractors
.Numerische Mathematik , 1997 , 75 (3 ): 293 -317
[19]
Dellnitz M Klus S Ziessler A et al .A set-oriented numerical approach for dynamical systems with parameter uncertainty
.SIAM Journal on Applied Dynamical Systems , 2017 , 16 (1 ): 120 -138
[20]
Doedel EJ Champneys AR Fairgrieve TF et al. Auto97: Continuation and bifurcation software for ordinary differential equations.
1997 . Auto97: Continuation and bifurcation software for ordinary differential equations. 1997.
URL
[本文引用: 1]
[21]
Guckenheimer J Vladimirsky A A fast method for approximating invariant manifolds
. SIAM Journal on Applied Dynamical Systems , 2004 , 3 (3 ): 232 -260
[本文引用: 5]
[22]
Peraire J Peiró J Morgan K. Advancing front grid generation//Handbook of Grid Generation. Boca Raton, FL : CRC Press , 1998
[23]
Frey P George PL. Mesh Generation 2nd ed. Wiltshire:
Wiley-ISTE , 2008
[24]
Henderson ME Computing invariant manifolds by integrating fat trajectories
.SIAM Journal on Applied Dynamical Systems , 2005 , 4 (4 ): 832 -882
[本文引用: 1]
[25]
James JM Polynomial approximation of one parameter families of (un)stable manifolds with rigorous computer assisted error bounds
.Indagationes Mathematicae , 2015 , 26 (1 ): 225 -265
[26]
van den Berg JB James JDM Reinhardt C Computing (un)stable manifolds with validated error bounds: Non-resonant and resonant spectra
.Journal of Nonlinear Science , 2016 , 26 (4 ): 1055 -1095
[27]
Haro À Canadell M Figueras JL et al. The Parameterization Method for Invariant Manifolds : From Rigorous Results to Effective Computations. New York: Springer International Publishing , 2016
[28]
Cabré X The parameterization method for invariant manifolds iii: overview and applications
.Journal of Differential Equations , 2005 , 218 (2 ): 444 -515
[29]
李清都 , 杨晓松 . 二维不稳定流形的计算
. 计算物理 , 2005 , 22 (6 ): 79 -84
[本文引用: 1]
(Li Qingdu Yang Xiaosong Computation of two dimensional unstable manifolds
.Chinese Journal of Computational Physics 2005 , 22 (6 ): 79 -84 (in Chinese))
[本文引用: 1]
[30]
贾蒙 , 樊养余 , 李慧敏 . 基于自适应因子轨道延拓法的不变流形计算
. 物理学报 , 2010 , 59 (11 ): 7686 -7692
[本文引用: 1]
(Jia Meng Fan Yangyu Li Huimin Computation of invariant manifolds with self-adaptive parameter and trajectories continuation method
.Acta Physica Sinica 2010 , 59 (11 ): 7686 -7692 (in Chinese))
[本文引用: 1]
[31]
孙恒义 , 樊养余 , 李慧敏 等 . 基于径向增长因子的二维不变流形计算
. 计算物理 , 2011 , 28 (4 ): 621 -625
[本文引用: 2]
(Sun Hengyi Fan Yangyu Li Huimin et al .Computation of two-dimensional invariant manifolds with radial growth factor
.Chinese Journal of Computational Physics 2011 , 28 (4 ): 621 -625 (in Chinese))
[本文引用: 2]
[32]
李清都 , 杨晓松 . 一种二维不稳定流形的新算法及其应用
. 物理学报 , 2010 , 59 (3 ): 1416 -1422
(Li Qingdu Yang Xiaosong A new algorithm for computation of two-dimensional unstable manifolds and its applications
.Acta Physica Sinica 2010 , 59 (3 ): 1416 -1422 (in Chinese))
[33]
李清都 , 谭宇玲 , 杨芳艳 . 连续时间系统二维不稳定流形的异构算法
. 物理学报 , 2011 , 60 (3 ): 0302061 -0302067
(Li Qingdu Tan Yuling Yang Fangyan A heterogeneous computing algorithm for two-dimensional unstable manifolds of time-continuous systems
.Acta Physica Sinica 2011 , 60 (3 ): 0302061 -0302067 (in Chinese))
[34]
Strikwerda J Finite Difference Schemes and Partial Differential Equations. California: Wadsworth & Brooks/Cole Advanced Books and
Software , 1989
[本文引用: 1]
[35]
Worring M Smeulders AWM Digital curvature estimation
.CVGIP: Image Understanding , 1993 , 58 (3 ): 366 -382
[36]
Razdan A Bae M Curvature estimation scheme for triangle meshes using biquadratic bézier patches
.Computer-Aided Design , 2005 , 37 (14 ): 1481 -1491
[37]
Magid E Soldea O Rivlin E A comparison of gaussian and mean curvature estimation methods on triangular meshes of range image data
.Computer Vision and Image Understanding , 2007 , 107 (3 ): 139 -159
[38]
Meyer M Desbrun M Schröder P et al .Discrete Differential-Geometry Operators for Triangulated 2-manifolds. Berlin,
Heidelberg: Springer , 2003
[本文引用: 1]
[39]
Pinsky T On the topology of the lorenz system//Proceedings of the Royal Society A: volume 473
. The Royal Society , 2017
[本文引用: 1]
[40]
Zaborszky J Huang G Zheng B et al .A counterexample of a theorem by tsolas et al. and an independent result by zaborszky et al
. IEEE Transactions on Automatic Control , 1988 , 33 (3 ): 316 -317
[本文引用: 1]
Invariant manifolds and global bifurcations
1
2015
... 稳定和不稳定流形是非线性动力系统的重要几何结构,是研究动力系统全局动态特性的重要工具 [1 ] . 稳定和不稳定流形的计算在动力系统分析和控制系统设计等领域有重要应用 [2-7 ] ,例如非线性系统稳定平衡点的稳定域的边界可由边界上不稳定平衡点的稳定流形获得 [8-11 ] . 不稳定流形可看作稳定流形的时间反向,因此本文重点研究稳定流形的情形. ...
高维非线性映射系统的不稳定流形计算方法研究
2017
高维非线性映射系统的不稳定流形计算方法研究
2017
Aircraft nonlinear stability analysis and multidimensional stability region estimation under icing conditions
2017
基于多项式约束的三角平动点平面周期轨道设计方法
2017
基于多项式约束的三角平动点平面周期轨道设计方法
2017
On the number of unstable equilibrium points on spatially-periodic stability boundary
2016
积冰对飞机本体纵向非线性动力学稳定域的影响
2017
积冰对飞机本体纵向非线性动力学稳定域的影响
2017
On the number and types of unstable equilibria in nonlinear dynamical systems with uniformly-bounded stability regions
2016
Characterization of stability region for general autonomous nonlinear dynamical systems
2012
A survey of methods for computing (un)stable manifolds of vector fields
1
2005
... 一般系统的全局稳定流形无法得到解析表达式,并且稳定流形无法通过隐式方法计算 [12 ] . 稳定流形定理 [13-14 ] 表明,系统的稳定流形与其线性化系统的稳定特征子空间在平衡点处相切. 因此可以由稳定特征子空间上平衡点的邻域出发,通过迭代计算系统的稳定流形. 最直接的迭代方法是简单积分法,即以稳定特征子空间上的一个椭圆作为稳定流形的初始估计 M 0 M 0 Δ t Δ s M 1 M i M i + 1 M i + 1 M i + 1 M i
Elements of Applied Bifurcation Theory. 2nd ed
1998
Holmes. Nonlinear oscillations, dynamical systems and bifurcations of vector fields. 2nd ed. NY:
1986
Two-dimensional invariant manifolds and global bifurcations: Some approximation and visualization studies
1
1997
... 为克服简单积分法的局限性,一些适用性较强的算法被相继提出. 轨道弧长算法 [15 ] 将向量场各方向的生长速度归一化,使得轨道沿各方向同速生长. 然而轨道的生长仍然受制于系统向量场,相邻的初始点也可能产生较大的分离. 测地水平集算法 [16-17 ] 通过在 M i M i + 1 M i + 1 M i [18-19 ] 可以较容易地确定流形的轮廓,但该 算法无法反映出流形的增长趋势. 边值问题(BVP)连续算法 [20 ] 基于微分方程解的连续性,利用轨道扫描出流形面,因此该算法将在近平衡点处产生大量的点,需要对计算结果进行相应的后期处理. 偏微分方程(偏微分方程)算法 [21 ] 借鉴前沿推进网格生成算法 [22-23 ] ,该算法对流形网格具有较好的控制能力,计算效率较高. 此外还有扩展轨迹算法 [24 ] ,参数化算法等 [25-28 ] . 国内方面,两步法 [29 ] 的第一步通过求解初值问题快速确定流形上点的位置,第二步则利用第一步计算出的点勾画流形的图像. 自适应因子轨道延拓算法 [30 ] 根据计算的精度要求自适应的调整轨道的数目,以保证轨道间距小于误差限. 该算法中轨道上的点是等间距的. 误差限和轨道点间距都是全局统一的,没有根据流形曲率进行调整. 径向增长控制算法 [31 ] 通过引入径向控制因子将原始动力学系统进行归一化,使得各方向的轨道生长速度相同. 异构算法 [32-33 ] 利用相邻的取样轨道连接形成三角形构成局部流形,但其取样轨道间的距离限制和轨道点间距也是全局 统一的,没有根据流形曲率进行调整. ...
Computing geodesic level sets on global (un)stable manifolds of vector fields
2003
Dynamical systems: Some computational problems
1993
A subdivision algorithm for the computation of unstable manifolds and global attractors
1997
A set-oriented numerical approach for dynamical systems with parameter uncertainty
2017
Auto97: Continuation and bifurcation software for ordinary differential equations.
1
1997
... 为克服简单积分法的局限性,一些适用性较强的算法被相继提出. 轨道弧长算法 [15 ] 将向量场各方向的生长速度归一化,使得轨道沿各方向同速生长. 然而轨道的生长仍然受制于系统向量场,相邻的初始点也可能产生较大的分离. 测地水平集算法 [16-17 ] 通过在 M i M i + 1 M i + 1 M i [18-19 ] 可以较容易地确定流形的轮廓,但该 算法无法反映出流形的增长趋势. 边值问题(BVP)连续算法 [20 ] 基于微分方程解的连续性,利用轨道扫描出流形面,因此该算法将在近平衡点处产生大量的点,需要对计算结果进行相应的后期处理. 偏微分方程(偏微分方程)算法 [21 ] 借鉴前沿推进网格生成算法 [22-23 ] ,该算法对流形网格具有较好的控制能力,计算效率较高. 此外还有扩展轨迹算法 [24 ] ,参数化算法等 [25-28 ] . 国内方面,两步法 [29 ] 的第一步通过求解初值问题快速确定流形上点的位置,第二步则利用第一步计算出的点勾画流形的图像. 自适应因子轨道延拓算法 [30 ] 根据计算的精度要求自适应的调整轨道的数目,以保证轨道间距小于误差限. 该算法中轨道上的点是等间距的. 误差限和轨道点间距都是全局统一的,没有根据流形曲率进行调整. 径向增长控制算法 [31 ] 通过引入径向控制因子将原始动力学系统进行归一化,使得各方向的轨道生长速度相同. 异构算法 [32-33 ] 利用相邻的取样轨道连接形成三角形构成局部流形,但其取样轨道间的距离限制和轨道点间距也是全局 统一的,没有根据流形曲率进行调整. ...
A fast method for approximating invariant manifolds
5
2004
... 为克服简单积分法的局限性,一些适用性较强的算法被相继提出. 轨道弧长算法 [15 ] 将向量场各方向的生长速度归一化,使得轨道沿各方向同速生长. 然而轨道的生长仍然受制于系统向量场,相邻的初始点也可能产生较大的分离. 测地水平集算法 [16-17 ] 通过在 M i M i + 1 M i + 1 M i [18-19 ] 可以较容易地确定流形的轮廓,但该 算法无法反映出流形的增长趋势. 边值问题(BVP)连续算法 [20 ] 基于微分方程解的连续性,利用轨道扫描出流形面,因此该算法将在近平衡点处产生大量的点,需要对计算结果进行相应的后期处理. 偏微分方程(偏微分方程)算法 [21 ] 借鉴前沿推进网格生成算法 [22-23 ] ,该算法对流形网格具有较好的控制能力,计算效率较高. 此外还有扩展轨迹算法 [24 ] ,参数化算法等 [25-28 ] . 国内方面,两步法 [29 ] 的第一步通过求解初值问题快速确定流形上点的位置,第二步则利用第一步计算出的点勾画流形的图像. 自适应因子轨道延拓算法 [30 ] 根据计算的精度要求自适应的调整轨道的数目,以保证轨道间距小于误差限. 该算法中轨道上的点是等间距的. 误差限和轨道点间距都是全局统一的,没有根据流形曲率进行调整. 径向增长控制算法 [31 ] 通过引入径向控制因子将原始动力学系统进行归一化,使得各方向的轨道生长速度相同. 异构算法 [32-33 ] 利用相邻的取样轨道连接形成三角形构成局部流形,但其取样轨道间的距离限制和轨道点间距也是全局 统一的,没有根据流形曲率进行调整. ...
... 则 W s ( x 0 ) g ( x 1 , x 2 ) - x 3 = 0 x [21 ] ...
... 则三角形 v 1 v 2 v v v . 可见问题最终转化为求解方程(7)中的未知数 α . 另外,为保证算法的稳定性和精度,点 v [34 ] 才能被接受为已知点 [21 ] . ...
... 根据相切条件,可以在稳定流形的前沿得到一个新的三角单元作为局部估计,并且估计的误差阶数为 O ( Δ 2 ) Δ [21 ] . 当稳定流形某部分卷曲程度高于其他部分时,就要求相应的估计误差小于其他部分. 因此必须根据稳定流形的曲率来自适应的调整三角单元的尺寸. 在估计离散曲率的诸多算法中 [35-37 ] ,Meyer 的方法几何意义简明且便于三角网格实现,因此本文采用Meyer方法来估计稳定流形的平均曲率 [38 ] . ...
... 单元尺寸自适应的引入提高了算法对流形曲率变化的适应性,同时也对算法的性能带来了影响. 在迭代误差方面,若流形曲率持续减小,则网格单元尺寸会随之增大,迭代误差相应地增大,计算精度随之下降. 因此为保证算法的全局精度,应设置单元尺寸的上限(本文中设置为初始尺寸的二倍). 偏微分方程算法的全局误差阶数为 O ( Δ ) [21 ] ,设置网格单元尺寸上限后,本文算法也可获得全局一阶精度. 在计算量方面,如果流形曲率急剧增大,则本算法使用的网格单元的尺寸就会急剧减小,为计算至指定轨线长度,所需的网格单元数将显著增多,计算量也将随之急剧增加. 实际编程实现中,可以通过设置单元尺寸的下限来防止计算量的急剧增加. 在计算速度方面,由于单元尺寸自适应本身需要额外的计算时间,并且单元尺寸的减小会增加计算网格数,因此本算法的计算速度比偏微分方程算法慢. ...
Computing invariant manifolds by integrating fat trajectories
1
2005
... 为克服简单积分法的局限性,一些适用性较强的算法被相继提出. 轨道弧长算法 [15 ] 将向量场各方向的生长速度归一化,使得轨道沿各方向同速生长. 然而轨道的生长仍然受制于系统向量场,相邻的初始点也可能产生较大的分离. 测地水平集算法 [16-17 ] 通过在 M i M i + 1 M i + 1 M i [18-19 ] 可以较容易地确定流形的轮廓,但该 算法无法反映出流形的增长趋势. 边值问题(BVP)连续算法 [20 ] 基于微分方程解的连续性,利用轨道扫描出流形面,因此该算法将在近平衡点处产生大量的点,需要对计算结果进行相应的后期处理. 偏微分方程(偏微分方程)算法 [21 ] 借鉴前沿推进网格生成算法 [22-23 ] ,该算法对流形网格具有较好的控制能力,计算效率较高. 此外还有扩展轨迹算法 [24 ] ,参数化算法等 [25-28 ] . 国内方面,两步法 [29 ] 的第一步通过求解初值问题快速确定流形上点的位置,第二步则利用第一步计算出的点勾画流形的图像. 自适应因子轨道延拓算法 [30 ] 根据计算的精度要求自适应的调整轨道的数目,以保证轨道间距小于误差限. 该算法中轨道上的点是等间距的. 误差限和轨道点间距都是全局统一的,没有根据流形曲率进行调整. 径向增长控制算法 [31 ] 通过引入径向控制因子将原始动力学系统进行归一化,使得各方向的轨道生长速度相同. 异构算法 [32-33 ] 利用相邻的取样轨道连接形成三角形构成局部流形,但其取样轨道间的距离限制和轨道点间距也是全局 统一的,没有根据流形曲率进行调整. ...
Polynomial approximation of one parameter families of (un)stable manifolds with rigorous computer assisted error bounds
2015
Computing (un)stable manifolds with validated error bounds: Non-resonant and resonant spectra
2016
The parameterization method for invariant manifolds iii: overview and applications
2005
二维不稳定流形的计算
1
2005
... 为克服简单积分法的局限性,一些适用性较强的算法被相继提出. 轨道弧长算法 [15 ] 将向量场各方向的生长速度归一化,使得轨道沿各方向同速生长. 然而轨道的生长仍然受制于系统向量场,相邻的初始点也可能产生较大的分离. 测地水平集算法 [16-17 ] 通过在 M i M i + 1 M i + 1 M i [18-19 ] 可以较容易地确定流形的轮廓,但该 算法无法反映出流形的增长趋势. 边值问题(BVP)连续算法 [20 ] 基于微分方程解的连续性,利用轨道扫描出流形面,因此该算法将在近平衡点处产生大量的点,需要对计算结果进行相应的后期处理. 偏微分方程(偏微分方程)算法 [21 ] 借鉴前沿推进网格生成算法 [22-23 ] ,该算法对流形网格具有较好的控制能力,计算效率较高. 此外还有扩展轨迹算法 [24 ] ,参数化算法等 [25-28 ] . 国内方面,两步法 [29 ] 的第一步通过求解初值问题快速确定流形上点的位置,第二步则利用第一步计算出的点勾画流形的图像. 自适应因子轨道延拓算法 [30 ] 根据计算的精度要求自适应的调整轨道的数目,以保证轨道间距小于误差限. 该算法中轨道上的点是等间距的. 误差限和轨道点间距都是全局统一的,没有根据流形曲率进行调整. 径向增长控制算法 [31 ] 通过引入径向控制因子将原始动力学系统进行归一化,使得各方向的轨道生长速度相同. 异构算法 [32-33 ] 利用相邻的取样轨道连接形成三角形构成局部流形,但其取样轨道间的距离限制和轨道点间距也是全局 统一的,没有根据流形曲率进行调整. ...
二维不稳定流形的计算
1
2005
... 为克服简单积分法的局限性,一些适用性较强的算法被相继提出. 轨道弧长算法 [15 ] 将向量场各方向的生长速度归一化,使得轨道沿各方向同速生长. 然而轨道的生长仍然受制于系统向量场,相邻的初始点也可能产生较大的分离. 测地水平集算法 [16-17 ] 通过在 M i M i + 1 M i + 1 M i [18-19 ] 可以较容易地确定流形的轮廓,但该 算法无法反映出流形的增长趋势. 边值问题(BVP)连续算法 [20 ] 基于微分方程解的连续性,利用轨道扫描出流形面,因此该算法将在近平衡点处产生大量的点,需要对计算结果进行相应的后期处理. 偏微分方程(偏微分方程)算法 [21 ] 借鉴前沿推进网格生成算法 [22-23 ] ,该算法对流形网格具有较好的控制能力,计算效率较高. 此外还有扩展轨迹算法 [24 ] ,参数化算法等 [25-28 ] . 国内方面,两步法 [29 ] 的第一步通过求解初值问题快速确定流形上点的位置,第二步则利用第一步计算出的点勾画流形的图像. 自适应因子轨道延拓算法 [30 ] 根据计算的精度要求自适应的调整轨道的数目,以保证轨道间距小于误差限. 该算法中轨道上的点是等间距的. 误差限和轨道点间距都是全局统一的,没有根据流形曲率进行调整. 径向增长控制算法 [31 ] 通过引入径向控制因子将原始动力学系统进行归一化,使得各方向的轨道生长速度相同. 异构算法 [32-33 ] 利用相邻的取样轨道连接形成三角形构成局部流形,但其取样轨道间的距离限制和轨道点间距也是全局 统一的,没有根据流形曲率进行调整. ...
基于自适应因子轨道延拓法的不变流形计算
1
2010
... 为克服简单积分法的局限性,一些适用性较强的算法被相继提出. 轨道弧长算法 [15 ] 将向量场各方向的生长速度归一化,使得轨道沿各方向同速生长. 然而轨道的生长仍然受制于系统向量场,相邻的初始点也可能产生较大的分离. 测地水平集算法 [16-17 ] 通过在 M i M i + 1 M i + 1 M i [18-19 ] 可以较容易地确定流形的轮廓,但该 算法无法反映出流形的增长趋势. 边值问题(BVP)连续算法 [20 ] 基于微分方程解的连续性,利用轨道扫描出流形面,因此该算法将在近平衡点处产生大量的点,需要对计算结果进行相应的后期处理. 偏微分方程(偏微分方程)算法 [21 ] 借鉴前沿推进网格生成算法 [22-23 ] ,该算法对流形网格具有较好的控制能力,计算效率较高. 此外还有扩展轨迹算法 [24 ] ,参数化算法等 [25-28 ] . 国内方面,两步法 [29 ] 的第一步通过求解初值问题快速确定流形上点的位置,第二步则利用第一步计算出的点勾画流形的图像. 自适应因子轨道延拓算法 [30 ] 根据计算的精度要求自适应的调整轨道的数目,以保证轨道间距小于误差限. 该算法中轨道上的点是等间距的. 误差限和轨道点间距都是全局统一的,没有根据流形曲率进行调整. 径向增长控制算法 [31 ] 通过引入径向控制因子将原始动力学系统进行归一化,使得各方向的轨道生长速度相同. 异构算法 [32-33 ] 利用相邻的取样轨道连接形成三角形构成局部流形,但其取样轨道间的距离限制和轨道点间距也是全局 统一的,没有根据流形曲率进行调整. ...
基于自适应因子轨道延拓法的不变流形计算
1
2010
... 为克服简单积分法的局限性,一些适用性较强的算法被相继提出. 轨道弧长算法 [15 ] 将向量场各方向的生长速度归一化,使得轨道沿各方向同速生长. 然而轨道的生长仍然受制于系统向量场,相邻的初始点也可能产生较大的分离. 测地水平集算法 [16-17 ] 通过在 M i M i + 1 M i + 1 M i [18-19 ] 可以较容易地确定流形的轮廓,但该 算法无法反映出流形的增长趋势. 边值问题(BVP)连续算法 [20 ] 基于微分方程解的连续性,利用轨道扫描出流形面,因此该算法将在近平衡点处产生大量的点,需要对计算结果进行相应的后期处理. 偏微分方程(偏微分方程)算法 [21 ] 借鉴前沿推进网格生成算法 [22-23 ] ,该算法对流形网格具有较好的控制能力,计算效率较高. 此外还有扩展轨迹算法 [24 ] ,参数化算法等 [25-28 ] . 国内方面,两步法 [29 ] 的第一步通过求解初值问题快速确定流形上点的位置,第二步则利用第一步计算出的点勾画流形的图像. 自适应因子轨道延拓算法 [30 ] 根据计算的精度要求自适应的调整轨道的数目,以保证轨道间距小于误差限. 该算法中轨道上的点是等间距的. 误差限和轨道点间距都是全局统一的,没有根据流形曲率进行调整. 径向增长控制算法 [31 ] 通过引入径向控制因子将原始动力学系统进行归一化,使得各方向的轨道生长速度相同. 异构算法 [32-33 ] 利用相邻的取样轨道连接形成三角形构成局部流形,但其取样轨道间的距离限制和轨道点间距也是全局 统一的,没有根据流形曲率进行调整. ...
基于径向增长因子的二维不变流形计算
2
2011
... 为克服简单积分法的局限性,一些适用性较强的算法被相继提出. 轨道弧长算法 [15 ] 将向量场各方向的生长速度归一化,使得轨道沿各方向同速生长. 然而轨道的生长仍然受制于系统向量场,相邻的初始点也可能产生较大的分离. 测地水平集算法 [16-17 ] 通过在 M i M i + 1 M i + 1 M i [18-19 ] 可以较容易地确定流形的轮廓,但该 算法无法反映出流形的增长趋势. 边值问题(BVP)连续算法 [20 ] 基于微分方程解的连续性,利用轨道扫描出流形面,因此该算法将在近平衡点处产生大量的点,需要对计算结果进行相应的后期处理. 偏微分方程(偏微分方程)算法 [21 ] 借鉴前沿推进网格生成算法 [22-23 ] ,该算法对流形网格具有较好的控制能力,计算效率较高. 此外还有扩展轨迹算法 [24 ] ,参数化算法等 [25-28 ] . 国内方面,两步法 [29 ] 的第一步通过求解初值问题快速确定流形上点的位置,第二步则利用第一步计算出的点勾画流形的图像. 自适应因子轨道延拓算法 [30 ] 根据计算的精度要求自适应的调整轨道的数目,以保证轨道间距小于误差限. 该算法中轨道上的点是等间距的. 误差限和轨道点间距都是全局统一的,没有根据流形曲率进行调整. 径向增长控制算法 [31 ] 通过引入径向控制因子将原始动力学系统进行归一化,使得各方向的轨道生长速度相同. 异构算法 [32-33 ] 利用相邻的取样轨道连接形成三角形构成局部流形,但其取样轨道间的距离限制和轨道点间距也是全局 统一的,没有根据流形曲率进行调整. ...
... 由图8 可知,利用本文所提算法计算稳定流形,所得流形网格在各方向上的推进速度大致是均衡的,不受系统向量场影响. 径向因子法 [31 ] 通过引入径向控制因子也能得到各项均衡发育的流形. 不同之处在于:径向因子法的主要目的是控制流形的径向增长速度,使得流形的发育在径向上是均衡的,而不关注流形网格单元尺寸对流形曲率的适应性;而本文算法的主要目的是让流形网格单元尺寸在全局范围根据流形曲率自适应地变化. 本文算法没有严格控制流形的径向生长速度,而是在算法步骤3中,选择距平衡点最近的流形备选点作为新的流形生长点,来大致平衡流形在各方向的生长发育. 在迭代的过程中,径向因子法实现了流形边缘到平衡点的径向距离相等,而本文算法则是使得流形前沿到平衡点的轨道长度相等. ...
基于径向增长因子的二维不变流形计算
2
2011
... 为克服简单积分法的局限性,一些适用性较强的算法被相继提出. 轨道弧长算法 [15 ] 将向量场各方向的生长速度归一化,使得轨道沿各方向同速生长. 然而轨道的生长仍然受制于系统向量场,相邻的初始点也可能产生较大的分离. 测地水平集算法 [16-17 ] 通过在 M i M i + 1 M i + 1 M i [18-19 ] 可以较容易地确定流形的轮廓,但该 算法无法反映出流形的增长趋势. 边值问题(BVP)连续算法 [20 ] 基于微分方程解的连续性,利用轨道扫描出流形面,因此该算法将在近平衡点处产生大量的点,需要对计算结果进行相应的后期处理. 偏微分方程(偏微分方程)算法 [21 ] 借鉴前沿推进网格生成算法 [22-23 ] ,该算法对流形网格具有较好的控制能力,计算效率较高. 此外还有扩展轨迹算法 [24 ] ,参数化算法等 [25-28 ] . 国内方面,两步法 [29 ] 的第一步通过求解初值问题快速确定流形上点的位置,第二步则利用第一步计算出的点勾画流形的图像. 自适应因子轨道延拓算法 [30 ] 根据计算的精度要求自适应的调整轨道的数目,以保证轨道间距小于误差限. 该算法中轨道上的点是等间距的. 误差限和轨道点间距都是全局统一的,没有根据流形曲率进行调整. 径向增长控制算法 [31 ] 通过引入径向控制因子将原始动力学系统进行归一化,使得各方向的轨道生长速度相同. 异构算法 [32-33 ] 利用相邻的取样轨道连接形成三角形构成局部流形,但其取样轨道间的距离限制和轨道点间距也是全局 统一的,没有根据流形曲率进行调整. ...
... 由图8 可知,利用本文所提算法计算稳定流形,所得流形网格在各方向上的推进速度大致是均衡的,不受系统向量场影响. 径向因子法 [31 ] 通过引入径向控制因子也能得到各项均衡发育的流形. 不同之处在于:径向因子法的主要目的是控制流形的径向增长速度,使得流形的发育在径向上是均衡的,而不关注流形网格单元尺寸对流形曲率的适应性;而本文算法的主要目的是让流形网格单元尺寸在全局范围根据流形曲率自适应地变化. 本文算法没有严格控制流形的径向生长速度,而是在算法步骤3中,选择距平衡点最近的流形备选点作为新的流形生长点,来大致平衡流形在各方向的生长发育. 在迭代的过程中,径向因子法实现了流形边缘到平衡点的径向距离相等,而本文算法则是使得流形前沿到平衡点的轨道长度相等. ...
Finite Difference Schemes and Partial Differential Equations. California: Wadsworth & Brooks/Cole Advanced Books and
1
1989
... 则三角形 v 1 v 2 v v v . 可见问题最终转化为求解方程(7)中的未知数 α . 另外,为保证算法的稳定性和精度,点 v [34 ] 才能被接受为已知点 [21 ] . ...
Digital curvature estimation
1993
Curvature estimation scheme for triangle meshes using biquadratic bézier patches
2005
A comparison of gaussian and mean curvature estimation methods on triangular meshes of range image data
2007
Discrete Differential-Geometry Operators for Triangulated 2-manifolds. Berlin,
1
2003
... 根据相切条件,可以在稳定流形的前沿得到一个新的三角单元作为局部估计,并且估计的误差阶数为 O ( Δ 2 ) Δ [21 ] . 当稳定流形某部分卷曲程度高于其他部分时,就要求相应的估计误差小于其他部分. 因此必须根据稳定流形的曲率来自适应的调整三角单元的尺寸. 在估计离散曲率的诸多算法中 [35-37 ] ,Meyer 的方法几何意义简明且便于三角网格实现,因此本文采用Meyer方法来估计稳定流形的平均曲率 [38 ] . ...
On the topology of the lorenz system//Proceedings of the Royal Society A: volume 473
1
2017
... 洛伦兹系统 [39 ] 是验证稳定流形算法的经典算例,其方程为 ...
A counterexample of a theorem by tsolas et al. and an independent result by zaborszky et al
1
1988