含芯拧绞绳非线性弯曲动力学特性分析与研究
ANALYSIS OF THE CORED STRANDED WIRE ROPE ON THE NONLINEAR BENDING DYNAMIC CHARACTERISTICS
中图分类号: O313.7
通讯作者:
收稿日期: 2017-09-1
接受日期: 2018-02-6
网络出版日期: 2018-02-10
版权声明: 2018 《力学学报》编辑部 《力学学报》编辑部 所有
基金资助:
展开
摘要
建立细长缆索大柔性多体动力学模型时,现实存在的复杂捻制几何构型多不予考虑,而是将柔索简化为材料均匀梁进行描述,致使运动仿真模型与物理实际存在一定差距. 为此,研究一种典型非线性拧绞绳股的大变形等效动力学建模方法,考虑准静态与大范围运动情况下绳股内的线接触,计算了受摩擦力及弯曲曲率影响的绳股可变弯曲刚度,通过等效梁模型避免了绳股精细建模时的大规模计算消耗. 基于连续介质力学与绝对节点坐标方法,建立了拧绞绳惯性广义坐标下的多柔体动力学模型. 为了验证等效模型的可行性,与基于有限段方法建立的精细模型进行对比仿真分析,通过位形验证了等效模型的精度. 进一步地,根据力载作用下的准静态构型,研究了特定构型绳股弯曲刚度沿轴向的分布规律;通过自重力下一端固定柔性绳摆自由运动仿真并与传统均匀梁模型相比,研究了模型弯曲特性的差异. 最后,根据能量守恒原理分析了摩擦耗散系统内各种能量间的相互转化. 拧绞绳大变形等效动力学模型能够提高绳索动力系统运动预测的仿真计算效率,还能为钢丝绳参数与构型设计提供依据.
关键词:
Abstract
When modeling the slender structures such as cable and tether with large flexibility, the complex twirling geometry in practical situation is usually ignored and the cable is simplified as a general beam with homogeneous material. In doing so, the result of dynamic simulation diverges from the physical significance. Therefore, this paper provides an equivalent dynamic method for the typical nonlinear helix wire strand considering the inner line contact under the static and large scale dynamic conditions. The variable bending stiffness affected by the contact friction and bending curvature is obtained through the equivalent constitutive law, by which the massive computation resulting from fine modeling method is able to be avoided. Based on the absolute nodal coordinate formulation, a series of the generalized coordinates have been selected to establish the dynamic differential equations. To verify the equivalent method, a fine strand model based on the finite segment element has been provided to test the accuracy according to the practical strand configuration. Furtherer, the distribution of the variable bending stiffness in practical strand under certain load is obtained through the quasi-static analysis. Compared with traditional ANCF model, the dynamic simulation of the one-tip-fixed equivalent beam under gravity coincides with the fact that the stiffness decreases as well as the flexibility increases in twirling strand. At last, the conversion among each kind of the energy component has been researched. The equivalent model of the twirling strand with large deformation can be used to improve the efficiency of the motion prediction in cable dynamic systems. Besides, the results provide the evidence for wire rope design.
Keywords:
引 言
拧绞绳 指由数根绳线单元按一定规则绞合、捻制成股的一束绳索[1]. 目前对拧绞绳力学性能的研究主要包括:风力载荷 输电线缆[2]、公路桥梁拉索、升降拖曳绳缆[3]等张拉结构的小范围振动分析与静态力学特性分析. 近年来随着绳系结构在空间机构中的广泛使用,其质轻、柔软、易折叠的特点使得钢丝绳、纤维绳更多 用于机械臂传动[4]、绳系卫星[5]、空间非合作目标[6]捕获等空间任务中. 由绳索组成的执行机构对操作、控制对象的运动控制精度与效率有一定影响,因此,本文旨在研究绳索微观力学特性并得到符合 其实际构型的大变形动力学描述.
绳索复杂的捻制几何构型会大大增加描述绳索柔性变形所需要的自由度,因而在动力学建模与求解时,很少以多根绳线捻制成型 的复合构型绳股为研究对象. 本文的研究重点之一是绳股大变形柔性体的动力学建模,目前,基于三维梁理论得到了一系列以绳股为研究对象的精细模型. 国内刘延柱和薛纭[7,8]对螺旋型大生物分子结构进行了基于Kirchhoff弹性杆理论的动力学模拟,推导了受拉、 扭细杆的等效弯曲及等效扭转刚度. 20世纪末,为了从传统Kirchhoff-Love杆理论延伸出更易参数化的三维梁方法,Simo[9]在Reissner[10]的基础上提 出了完全几何精确梁方法,梁的初始曲率及初始截面形状可任意选取,截面转动由欧拉角或四元数给定. 但是偏微分形式的几何精确梁控制方程不适合多体动力学问题的求解,需要将连续模型通过数值离散的方法改进为便于实施动力 学仿真的模型,尤其是梁单元转动自由度的表现形式[11]. 其中,Shabana等[12,13]提出的绝对节点坐标方法(absolute nodal coordinate formulation,ANCF)通过梯度定义了全局系下的转动运动与弹性变形,从而避免了小转角、小应变对模型变形描述的限制,并发展 了一系列三维梁单元模型[14,15].
许多学者根据梁理论研究了典型螺旋形拧绞绳的动力学建模方法. Foti等[16,17]对历经大转动运动的绳索在共旋坐 标系下表示了部分运动自由度,结合几何精确梁方法改进了两种传统模型在处理运动耦合上的缺陷,分析了源于几何、材料及环 境载荷等因素的梁非线性响应,但受到小应变限制,难以做到柔索运动的实时仿真计算. 类似地,Provasi与Martins[18]建立了螺旋曲梁单元,充分考虑了绳索内部的弯曲、扭转耦合,避免了剪切闭锁. Wang等[3]直接把拧绞绳离散为由刚体质点组成的系统,将螺旋构型的质量--弹簧模型集成在计算机辅助设计软件中实现了拧 绞绳的快速建模与运动学实时仿真.
除了考虑三维梁模型自身几何材料非线性、单元描述不当导致的应变耦合[19]等影响,在数值仿真中能够动态地确定多组 元绳股内梁--梁之间接触、摩擦的分布状态才能从本质上提高绳股动力学模型强非线性描述的准确性. Gnanavel等[20]给出了单层拧绞绳绳芯--绳线之间的详细径向接触力、及其引起的切向接触应力与绳芯 受压变形的细杆平衡方程. Hong等[21]严格推导了复杂螺旋几何与梁假设条件、滑动曲率上界之间的关系. 更一般的拧绞绳包含多层,为了增强抗磨损性能,相邻两层交叉捻制,Lalonde等[22,23]据此引入了多级摩擦系数, 使绳股的弯曲刚度在最大与最小值之间平滑地更加变化,通过有限元疲劳计算估计了风载荷激励下输电线缆的使用寿命.
显然,三维梁模型一旦引入接触摩擦力后不可避免会增加绳股运动动态捕获过程中的数值计算消耗,所以上述研究的对象大多跨 度、运动范围较小,且难以进行高效多体动力学仿真. 本文提出了针对大变形拧绞绳的一维介质等效梁模型,在同时考虑绳股微观捻制几何与接触分布的前提下,采用ANCF柔性梁离散方法推导拧绞绳多柔体动力学模型. 为了验证等效模型,基于有限段梁离散方法[24]建立了拧绞绳精细模型. 另一方面,与传统ANCF梁模型对比,输出大柔性绳股在大范围运动中的运动、变形及能量变化曲线. 结果表明,等效模型高效预测了强非线性绳股的运动规律且在宏观层面体现出拧绞绳的微观力学特性.
1 绳股非线性弯曲模型
引起拧绞绳弯曲刚度非线性的主要原因在于张紧状态下绳线之间存在法向接触压力产生的切向摩擦[25]. 弯曲变形较小时, 材料内部弹性力足以平衡摩擦力,绳线之间无相对滑动;当变形继续增大,绳股截面上不同相位处的绳线先后出现相对滑动, 绳股内部的受力因此会在完全黏滞、部分滑动与完全滑动三个阶段之间切换[26],弯曲刚度特性也随之改变. 本节将建立不同摩擦状态下绳股的非线性弯曲本构力学模型.
1.1 螺旋线几何构型
定义一根钢丝或细纤维束为组成拧绞绳的基本单元,即绳线单元,首先在绳股平直构型下建立螺旋线的几何关系. 经捻制、绞合得 到捻角为
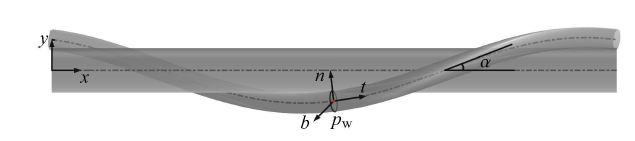
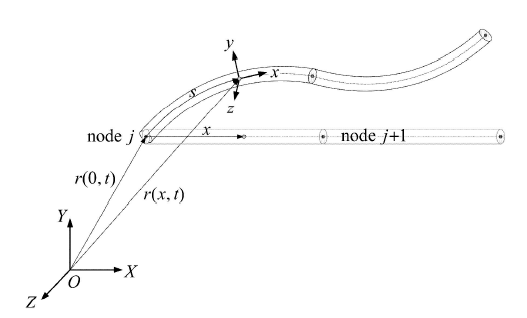
图1中,螺旋线形心轴的切线与绳股轴线的夹角
$ {\pmb r}_{p_{\rm w} } = \left[ {\dfrac{P}{2\pi }\left( {\varphi _{\rm w} - \varphi _{\rm w}^0 } \right),R_{\rm w} \sin \varphi _{\rm w},R_{\rm w} \cos \varphi _{\rm w} } \right]^{\rm T} (1) $
式中,点
为描述螺旋线曲梁截面特性,在点
$ {\pmb t} = \dfrac{{\pmb r}'_{p_{\rm W}} }{\sqrt {{\pmb r}'_{p_{\rm W} } \cdot {\pmb r}'_{p_{\rm W} } } } , \ \ \ {\pmb r}'_{p_{\rm W} } = \dfrac{d{\pmb r}_{p_{\rm W} } }{d s_{\rm w} }(2)$
螺旋线的弯曲程度由螺旋曲率矢量
$ {\pmb \kappa }_{\rm w} = \dfrac{d{\pmb t }}{ d s_{\rm w} } = \left| {{\pmb \kappa }_{\rm w} } \right|{\pmb n} = \kappa _{\rm w} {\pmb n} (3) $
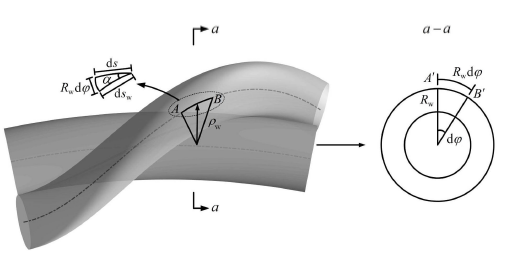
图2描述了螺旋线的局部几何特征,微弧段的螺旋曲率半径
图2 螺旋微弧段横截面投影
Fig. 2 Projection of the differential arc segment on the strand cross section
将式(4)代入式(2)和式(3)后分别对
$ \kappa _{\rm w} = \dfrac{\sin ^2\alpha }{R_{\rm w} } (5) $
1.2 基础结构弯曲模型
绳线由于自身的结构材料属性具有一定抗弯能力,对应无摩擦、完全滑动状态下的纯结构弯曲,是绳股变形过程中体现的最小 弯曲刚度. 绳芯为半径
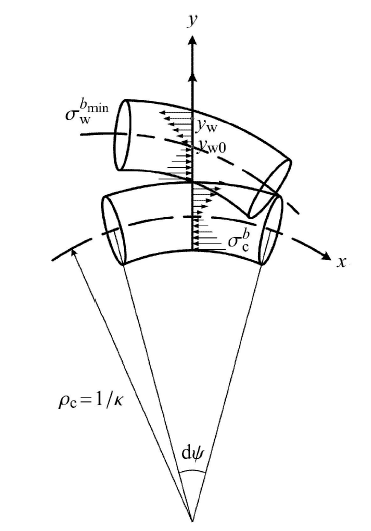
对发生图3中弯曲变形的绳股,微元段弯曲曲率
式中,
其在坐标系
根据应变张量坐标转换规律,这一应变可由以下关系得到
此时,可通过材料本构方程给出螺旋线沿形心轴的弯曲应力
式中,
进一步根据
式中,
绳股的基础弯曲模型是绳芯与全体螺旋线弯曲刚度的总和,则
1.3 附加弯曲模型
螺旋线沿绳芯成型后,依靠两者之间的接触摩擦阻碍相对滑移的出现以维持螺旋构型,接触摩擦引起螺旋线的附加变形在宏观 上也体现为绳股抗弯特性变化,是拧绞绳弯曲非线性的主要来源之一.
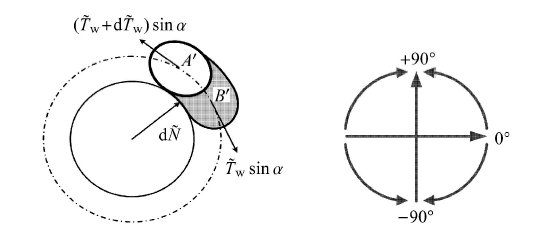
无摩擦作用时,绳线变形独立,当绳股受轴向拉伸,内部沿螺旋形心轴分布的轴向力会引起外层绳线对绳芯挤压,因此螺旋线 受到径向反作用力
根据库伦摩擦模型:
沿截面分布角积分,得到轴向拉力
继而得到其引起的螺旋线附加弯曲应力
螺旋线与绳芯之间接触状态为黏滞摩擦时,二者视为一个整体,对应的附加黏滞弯曲应变、弯曲应力可根据绳股曲率直接计算
绳股弯曲继续增大,当黏滞摩擦力不足以平衡螺旋线变形力时,黏滞摩擦转为滑动摩擦,对应的附加滑动弯曲应力与式(17)一致
两种状态下的附加弯曲应力在螺旋线截面上积分得到附加弯曲力矩
分别将式(19)与式(20)代入上式,最终得到绳股弯曲平面内的附加弯曲刚度
(22)
绳线接触摩擦黏滞与滑动状态相互转换的判定由临界曲率确定,临界条件下式(19)与式(20)相等
$ \kappa_{\rm c}=\dfrac{\tilde\sigma^{\rm a}_{\rm w}({\rm e}^{\mu \varphi _{\rm w} \sin \alpha }-1 )} {E_{\rm w}R_{\rm w} \sin \varphi_{\rm w}\cos^2 \alpha} (23)$
综上,本节给出了绳股绳线在不同接触状态下的弯曲非线性模型.
2 柔性多体动力学等效模型
柔性体的大变形动力学ANCF建模方法由Shabana[12]提出,与浮动坐标系方法所不同的是:节点处的广义坐标表示在绝对参 考坐标系下,转动与变形共同由位移梯度表示,得到的ANCF模型质量矩阵为常值矩阵,避免了柔性体描述方法对小转角、小应 变的限制. 本文基于ANCF一维介质梁模型描述其大弯曲变形过程,建立拧绞绳的等效模型. 等效模型根据绳线之间的微观力学状态与几何拓扑结构引入材料本构关系,绳线由均匀且各向同性的线弹性材料制成,假设螺 旋线的捻角与未变形平直状态保持一致.
2.1 绝对节点坐标梁位移场
ANCF一维梁模型的横截面保持刚性,连续梁经物理离散后每个单元的自由度在图5中绝对坐标系
取节点
$ {\pmb q} = \left[ {r_1 ,r_2 ,r_3 ,r_{1x} ,r_{2x} ,r_{3x} } \right]^{\rm T} , \ \ \ r_{kx} = \left. {\dfrac{\partial r_k }{\partial x}} \right|_{k = 1,2,3} (24) $
式中,
$ \left[ \!\!\begin{array}{c} {r_1 } \\ {r_2 } \\ {r_3 } \end{array}\!\!\right] = \left[\!\!\begin{array}{c} {a_0 + a_1 x + a_2 x^2 + a_3 x^3} \\ {b_0 + b_1 x + b_2 x^2 + b_3 x^3} \\ {c_0 + c_1 x + c_2 x^2 + c_3 x^3} \end{array}\!\! \right] (25) $
建立位置矢量
$ {\pmb r} = \left[ {S_1 {\pmb I}_3 } \ \ {S_2 {\pmb I}_3 } \ \ {S_3 {\pmb I }_3 } \ \ {S_4 {\pmb I}_3 } \right]\left[ \!\!\begin{array}{c} {{\pmb q}^1} {{\pmb q}^2} \end{array} \!\!\right] = {\pmb S} \left( x \right){\pmb q} (26) $
式中,形函数矩阵
$ \left.\!\!\begin{array}{c} S_1 = 1 - 3\xi ^2 + 2\xi ^3 , \ \ S_2 = L(\xi - 2\xi ^2 + \xi ^3) \\ S_3 = 3\xi ^2 - 2\xi ^3 , \ \ S_4 = L( - \xi ^2 + \xi ^3) \end{array}\!\!\right\} (27)$
式中,插值系数
2.2 单元广义弹性力
计算变刚度绳股的梁单元弹性力,需要在位于同一轴向物质坐标处对绳芯及螺旋线单元力进行加和. 基于连续介质力学原理, 在给定的虚应变上计算弹性力所做虚功. 为统一表示,将绳芯参量下标 c 用
$ \delta W_{\rm e} = \sum_{i = 0}^m \left( {\int_{V_i } \sigma _{{\rm w}i}^{\rm a} \delta \varepsilon d V_i + \int_{V_i } \sigma _{{\rm w}i}^{\rm b} \delta \kappa d V_i } \right) = \sum_{i = 0}^m \left[ {\int_{V_i } \left( {K_{{\rm w}i}^{\rm a} \varepsilon } \right)\dfrac{\partial \varepsilon }{\partial {\pmb q }} d V_i + \int_{V_i } \left( {K_{{\rm w}i}^{\rm b} \kappa } \right) \dfrac{\partial \kappa } {\partial {\pmb q}} d V_i } \right] \cdot \delta {\pmb q} = \left( {{\pmb Q}_{\rm e}^{\rm a} + {\pmb Q}_{\rm e}^{\rm b}} \right) \cdot \delta {\pmb q} \hskip46mm (28) $
式中,
关于轴向刚度系数
$ \varepsilon = \varepsilon _{\rm c}^{\rm a} = \varepsilon _{\rm w}^{\rm a} = \dfrac{\tilde {\varepsilon }_{\rm w}^{\rm a} }{\cos ^2\alpha } (29) $
根据式(29)分别建立绳芯与螺旋线的拉伸本构关系
式中,
将轴向刚度系数
$ {\pmb Q}_{\rm e}^{\rm a} = \int_0^L \left( {E_{\rm c} A_{\rm c} + m\eta E_{\rm w} A_{\rm w} } \right)\varepsilon \left( {\dfrac{\partial \varepsilon }{\partial {\pmb q}} } \right)^{\rm T} d x (32) $
弯曲广义弹性力
$ {\pmb Q}_{\rm e}^{{\rm b}_{\min } } = \int_0^L \left( {E_{\rm c} A_{\rm c} + m\eta E_{\rm w} A_{\rm w} } \right)\kappa \left( {\dfrac{\partial \kappa }{\partial {\pmb q}}} \right)^{\rm T} d x (33) $
由于每根螺旋线与绳芯的接触状态不一致,有的与绳芯间相对静止而有的出现相对滑动,需要根据临界曲率对螺旋线一一单独判断再加和方可得到绳股附加广义弯曲弹性力.
$\kappa \leqslant \kappa _{\rm c} $ 时
$ {\pmb Q}_{{\rm e}i}^{{\rm b}_{\rm stick} } = \int_0^L \eta E_{\rm w} A_{\rm w} R_{\rm w}^2 \sin ^2\varphi _{{\rm w}i} \kappa \left( {\dfrac{\partial \kappa }{\partial {\pmb q}}} \right)^{\rm T} d x (34) $
$ \kappa > \kappa _{\rm c} $时
$ {\pmb Q}_{{\rm e}i}^{{\rm b}_{\rm slip} } = \int_0^L \eta A_{\rm w} \sigma _{\rm w}^{\rm a} \left( {{\rm e}^{\mu \varphi _{{\rm w}i} \sin \alpha } - 1} \right)R_{\rm w} \sin \varphi _{{\rm w}i} \left( {\dfrac{\partial \kappa }{\partial {\pmb q}}} \right)^{\rm T} d x (35) $
式中,螺旋线相位角
$\varphi _{{\rm w}i} \left( x \right) = \varphi _{{\rm w}i} \left( 0 \right) + \dfrac{2\pi x}{P_{\rm w} } (36)$
$\varphi _{{\rm w}i} \left( x \right) = \varphi _{{\rm w}\left( {i - 1} \right)} \left( x \right) + \dfrac{2\pi }{m} (37)$
2.3 单元应变能
进一步研究绳股运动变形过程中的弹性应变能,不考虑阻尼效应,每一时刻的应变能仅与当前广义变量状态相关,而与广义速度状态无关.
$ U_{\rm e} = \sum_{i = 0}^m \left[ {\int_{V_i } \left( {\int \sigma _{{\rm w}i}^{\rm a} d\varepsilon } \right) d V_i + \int_{V_i } \left( {\int \sigma _{{\rm w}i}^{\rm b} d\kappa } \right) d V_i } \right] (38) $
轴向本构关系为线性,轴向应变能由应变能密度在单元体积上的积分导出
$ U_{\rm e}^{\rm a} = \dfrac{1}{2}\int_0^l {\left( {E_{\rm c} A_{\rm c} + m\eta E_{\rm w}A_{\rm w} } \right)\varepsilon ^2 d x} (39) $
弯曲变形的基础应变能部分
$ U_{\rm e}^{{\rm b}_{\min } } = \sum_{i = 0}^m {\int_{V_i } {\left( {\int {\sigma _{{\rm w}i}^{{\rm b}_{\min } } d\kappa } } \right)d V_i } } = \dfrac{1}{2}\int_0^l {\left( {E_{\rm c} I_{\rm c} + m\eta E_{\rm w} I_{\rm w} } \right)\kappa ^2 d x} (40) $
同理计算弯曲变形的附加应变能部分
$ U_{{\rm e}i}^{{\rm b}_{\rm stick} } = \dfrac{1}{2}\int_0^l {\eta E_{\rm w} A_{\rm w} R_{\rm w}^2 \sin ^2\varphi _{{\rm w}i} \kappa ^2 d x} (41) $
$\kappa \leqslant \kappa _{\rm c} $时
$ U_{{\rm e}i}^{{\rm b}_{\rm slip} } = \int_0^l {\eta A_{\rm w} \sigma _{\rm w}^{\rm a} \left( { {\rm e}^{\mu \varphi _{{\rm w}i} \sin \alpha } - 1} \right)R_{\rm w} \sin \varphi _{{\rm w}i} \kappa d x} (42) $
2.4 绳股多柔体动力学方程组
由虚功原理计算广义惯性力虚功
$ \delta W_{\rm inertia} = \left( {\int_V \rho \ddot {\pmb r} \cdot \dfrac{\partial {\pmb r}}{\partial {\pmb q}}d V} \right) \cdot \delta {\pmb q} = \left( {{\pmb M}\ddot {\pmb q} } \right) \cdot \delta {\pmb q} (43) $
根据质量守恒,将单元惯性力的体积积分转化为沿物质坐标的一维积分,得到单元广义质量矩阵
$ {\pmb M} = \int_0^L {\rho \left( {A_{\rm c} + m\dfrac{A_{\rm w} }{\cos \alpha }} \right)\left( {{\pmb S}^{\rm T}{\pmb S}} \right) d x} (44) $
下面推导柔性多体系统外部作用力的广义形式,以分布载荷外力为例,等效至单元节点后的单元广义分布载荷虚功
$ \delta W_f = \int_V {\rho {\pmb g } \cdot \delta {\pmb r} d V} = {\pmb Q }_{\rm g} \cdot \delta {\pmb q} (45) $
依据达朗贝尔原理建立拧绞绳的梁单元动力学方程组
$ \delta W_{\rm inertia }^j + \delta W_{\rm e}^j - \delta W_{\rm g}^j = 0 (46) $
将单元方程组扩展至含约束的绳股柔性多体系统,引入拉格朗日乘子
$ \left[ \!\!\begin{array}{cc} {\pmb M} & {\pmb C }_{\rm q}^{\rm T} \\ {\pmb C }_{\pmb q} & {\bf 0} \end{array}\!\!\right]\left[\!\! \begin{array}{c} \ddot{\pmb q} \\ {\pmb \lambda } \end{array}\!\! \right] = \left[\!\! \begin{array}{c} {{\pmb Q}_{\rm g} - \left( {{\pmb Q}_{\rm e}^{\rm a} + {\pmb Q}_{\rm e}^{{\rm b}_{\min } } + {\pmb Q}_{\rm e}^{{\rm b}_{\rm add} } } \right)} \\ {{\pmb Q}_{\rm c} } \end{array} \!\! \right] (47)$
式中,
2.4 模型验证
为验证等效模型的精度,本文采用有限段离散梁方法建立拧绞绳精细模型进行对比. 精细模型中,对每根螺旋线进行独立建模,分别沿螺旋形心轴均匀划分出一定数目刚性小段,在单元两端处添加段间弹簧力以捕捉螺旋线柔性特征;螺旋线与绳芯之间引入接触摩擦力,模拟拧绞绳的内部摩擦力.
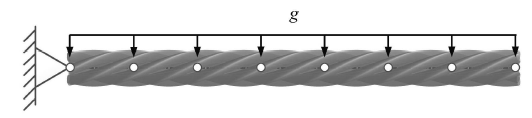
本文以1+6型钢丝绳为建模研究对象,结构与材料参数见表1. 将其一端固定,沿绳股轴线均匀加载
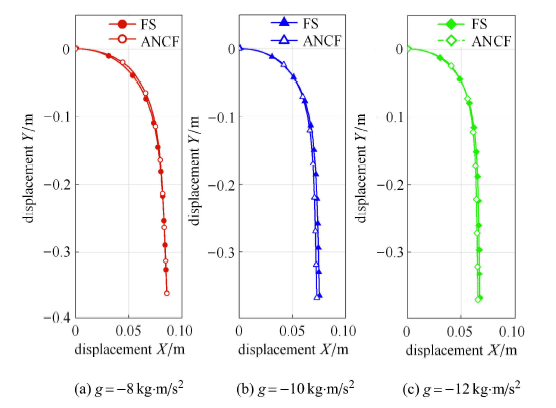
首先,研究不同大小载荷作用下的准静态构型,g分别取-8kg·m/s2,-10kg·m/s2与-12kg·m/s2. 对FS模型的独立螺旋线划分77个单元;对ANCF等效梁模型划分8个单元,所得结果如图7所示.
可知,等效模型在准静态构型上与精细模型的符合度较高. 随着力载的增大,拧绞绳根部弯曲变形逐渐加大,该区域内的变形描述是影响位形精度的主要因素,位置误差为10-3m,量级较小.
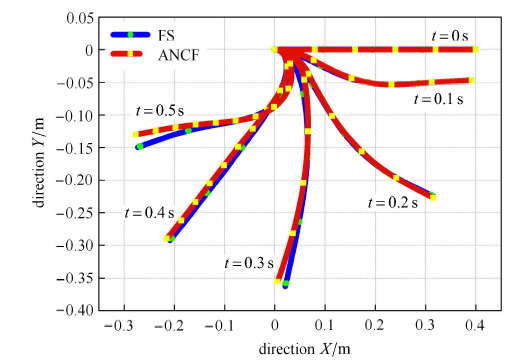
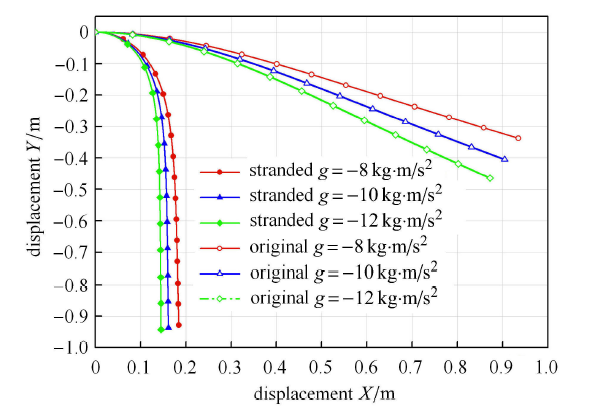
图8显示了自重力作用下,
两种方 法得到的位形在0
3 拧绞绳力学特性分析
3.1 悬臂梁静力学分析
在验证了等效模型可行性的基础上,本节进一步详细研究拧绞绳的力学特性,拧绞绳的结构与材料参数取值变为:绳长1 m、弹性模量2.0
首先,对绳股划分30个单元,研究准静态力学特性. 绳股上加载沿
静平衡状态下,绳股在运动平面内的位形如图9所示,等效模型在固定端根部的弯曲变形明显大于传统模型,整体沿
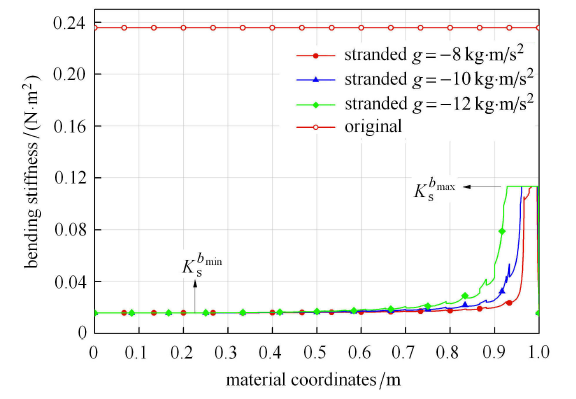
根据式(11)、式(22)导出受力平衡状态下绳股弯曲刚度沿轴向的分布,如图10所示. 可以看到等效ANCF模型反映出了绳股抗弯特性的变化,弯曲刚度随外力加载的差异沿不同路径在最小与最大值区间内变化,梁根部值对应式(11)的基础结构弯曲刚度,梁末端对应绳线间完全黏滞时包含式(22)中一式的最大弯曲刚度. 传统ANCF模型的弯曲刚度为常值,不因外力加载发生变化,其值高于等效ANCF模型的最大弯曲刚度.
图10 绳股弯曲刚度沿轴向分布
Fig. 10 Distribution of the strand bending stiffness along the axis line
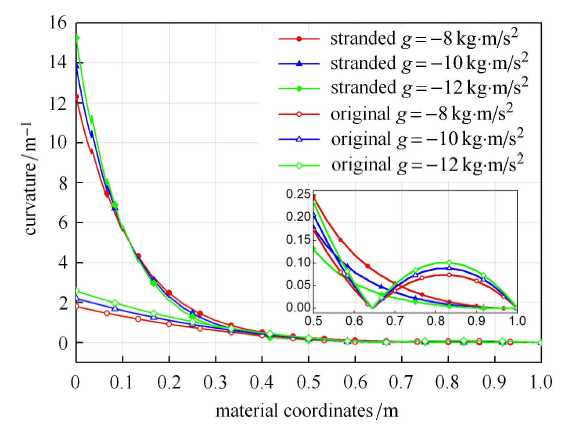
等效ANCF模型非线性弯曲刚度对应的接触状态主要依据弯曲曲率进行判定. 绳股曲率的分布如图11所示,等效模型在根部具有较大 弯曲变形,曲率大于全部绳线的临界值,处于滑动摩擦状态;0
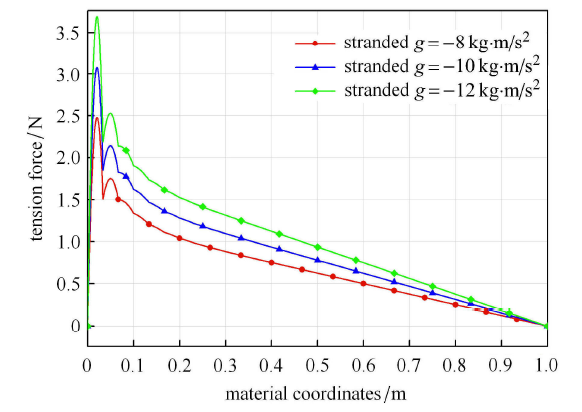
另一影响绳股附加弯曲刚度值的因素为轴向张紧力,如图12所示,它直接与绳线接触摩擦力相关. 选取g=-12kg
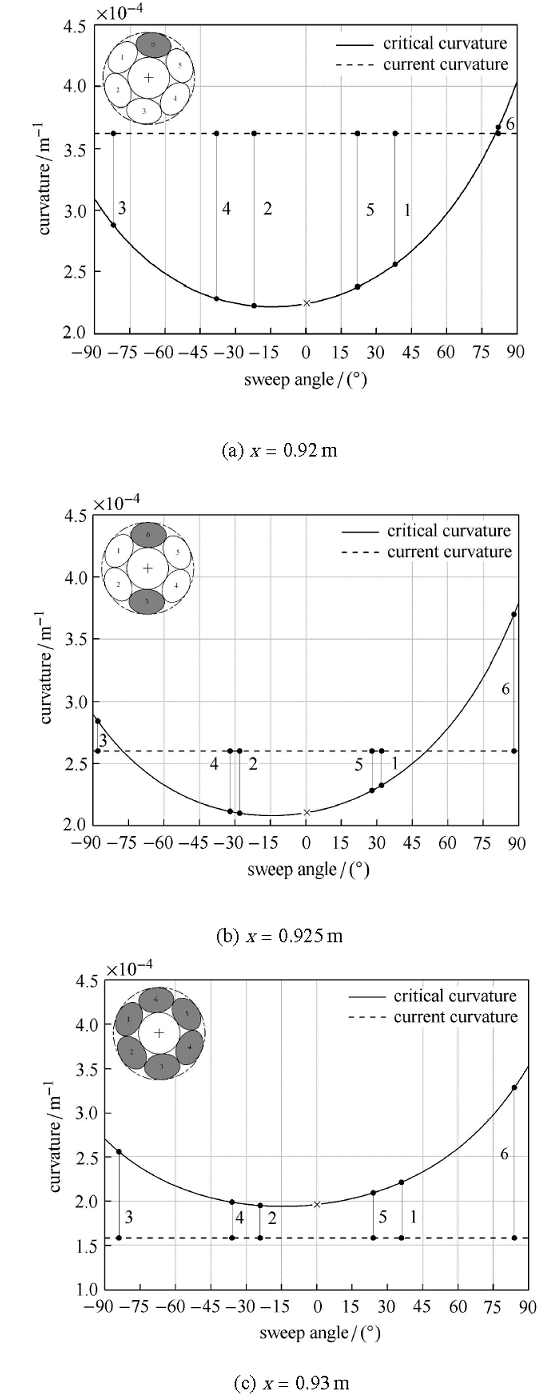
图13显示了特征点曲率与螺旋线临界曲率之间的关系,并根据式(36)与式(37)按逆时针标注出实际结构中螺旋线在绳股截面所 处位置与对应相位角,特征点当前弯曲曲率低于临界值的螺旋线对应黏滞接触摩擦状态,截面标注为深色. 显然,随着黏滞接触状态的螺旋线数目增大,绳股等效模型的弯曲刚度也逐步增大. 另外,临界曲率在绳股中性层上下部分的分布是不对称的,相位角小于0°的区域更易出现滑动.
3.2 柔性单摆自由运动仿真分析
上述静力学仿真分析从数值上验证了变化弯曲刚度的拧绞绳等效模型静态弯曲力学性能. 为了进一步研究等效模型在大范围运动中的动态非线性弯曲特性,将拧绞绳从水平静止状态释放,重力作用下做
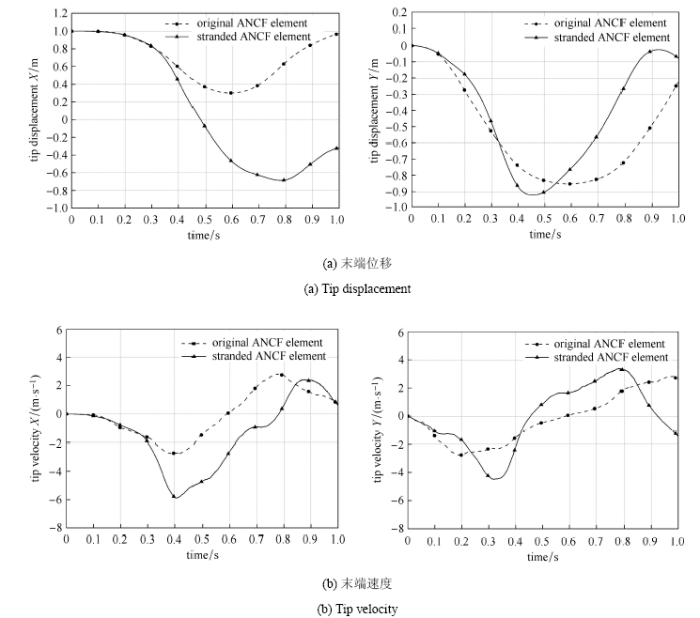
根据图14(a)中
图14(b)显示了绳股末端点速度变化曲线,等效模型沿水平、竖直方向上达到的最大速度大于传统模型,运动开始阶段0.2
图14 梁水平、竖直方向末端位移、速度
Fig.14 Tip displacement and velocity along the horizontal and vertical direction
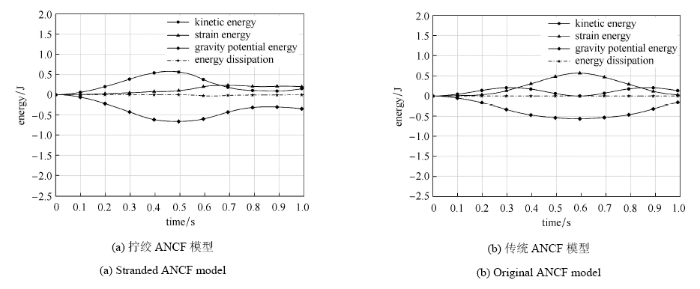
最后研究动态过程中系统各部分能量的变化,如图15所示. 图15 (a)中,等效ANCF模型的系统总能量略有下降,是由滑动 摩擦引起;图15 (b)中,传统ANCF模型忽略了绳股微观接触,因而为保守系统,满足能量守恒. 相对保守的传统模型而言,等效模型在运动仿真中能量曲线没有明显周期性变化.
综上,在拧绞绳大变形动力学建模的同时考虑螺旋线空间几何构型与微观接触摩擦,仿真结果体现了等效模型较强的弯曲非线性特性.
4 结 论
本文针对实际应用中具有捻制螺旋结构的拧绞钢丝绳研究了一种大变形等效动力学建模方法,经仿真验证得到以下五点结论:
(1)拧绞绳结构宏观力学特性复杂,具有较强的材料非均匀、非线性特性,通过对微观结构及受力的分析,得到了拧绞绳可变弯曲刚度模型;
(2)基于绝对节点坐标方法,建立了变刚度拧绞绳的大变形等效动力学模型,将绳股的捻制微观力学行为在大范围的宏观动力学特性中予以反映;
(3)通过与拧绞绳精细模型进行准静态与动态位形对比,验证了等效模型的可行性与精度;
(4)通过数值仿真分析了变刚度大变形梁模型动态过程中的运动规律、力学性能与能量转化,验证了等效模型由于接触状态的改变引起的模型抗弯特性变化及能量消耗;
(5)该等效模型避免了对螺旋线单元精细划再由接触力描述相互作用关系而导致的大规模运算消耗,可对多种边界条件下的绳股运动状态进行预测、验证、设计与分析.
The authors have declared that no competing interests exist.
参考文献
| [1] |
The Modelling and Analysis of the Mechanics of Ropes . |
| [2] |
Time history modeling of vibrations on overhead conductors with variable bending stiffness . |
| [3] |
A novel approach for modeling and simulation of helix twisting structure based on mass-spring model . |
| [4] |
带可控臂绳系卫星释放及姿态控制 .Deployment and attitude control of a tethered subsatellite with controllable arm . |
| [5] |
电动力绳系研究进展 .Review of electrodynamic tether system . |
| [6] |
空间大型末端执行器绳索捕获动力学建模与仿真 .Dynamic modeling and simulation on rope capturing by space large end effector . |
| [7] |
受拉扭弹性细杆超螺旋形态的定性分析 .Qualitive analysis of supercoiling configuration of a thin elastic rod under tension and twist . |
| [8] |
受圆柱面约束螺旋杆伸展为直杆的动力学分析 .Dynamical analysis of structural process of helical rod to straight rod under constraint of cylinder . |
| [9] |
A finite strain beam formulation. The three-dimensional dynamic problem. Part I . |
| [10] |
On one-dimensional finite-strain beam theory: the plane problem . |
| [11] |
A comparison of finite elements for nonlinear beams: the absolute nodal coordinate and geometrically exact formulations . |
| [12] |
Definition of the slopes and the finite element absolute nodal coordinate formulation . |
| [13] |
Three dimensional absolute nodal coordinate formulation for beam elements: theory . |
| [14] |
Structural and continuum mechanics approaches for a 3D shear deformable ANCF beam finite element: Application to buckling and nonlinear dynamic examples . |
| [15] |
Higher-order beam elements based on the absolute nodal coordinate formulation for three-dimensional elasticity . |
| [16] |
A corotational beam element and a refined mechanical model for the nonlinear dynamic analysis of cables. [PhD Thesis] . |
| [17] |
Numerical integration of the equations of motion of structural systems undergoing large 3D rotations: Dynamics of corotational slender beam elements . |
| [18] |
A three-dimensional curved beam element for helical components modeling . |
| [19] |
ANCF 索梁单元应变耦合问题与模型解耦 .The strain coupling problem and model decoupling of ANCF cable/beam element . |
| [20] |
Effect of interfacial contact forces in radial contact wire strand . |
| [21] |
Geometry and friction of helically wrapped wires in a cable subjected to tension and bending . |
| [22] |
Modeling multilayered wire strands, a strategy based on 3D finite element beam-to-beam contacts-Part I: Model formulation and validation . |
| [23] |
Modeling multilayered wire strands, a strategy based on 3D finite element beam-to-beam contacts-Part II: Application to wind-induced vibration and fatigue analysis of overhead conductors . |
| [24] |
Use of finite element and finite segment methods in modeling rail flexibility: a comparative study . |
| [25] |
Cable modeling and internal damping developments . |
| [26] |
Bending behavior of helically wrapped cables . |
| [27] |
Theoretical estimation of the response of helically armored cables to tension, torsion, and bending . |
| [28] |
Theory of Wire Rope . |
| [29] |
Transmission Line Reference Book: Wind Induced Conductor Motion . |
| [30] |
大变形柔性多体系统高效数值计算方法研究. [硕士论文] .Research on high efficient numerical algorithm of the flexible multibody dynamics with large deformation. [Master Thesis] . |

/
| 〈 |
|
〉 |