引 言
许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] .
近些年,我们围绕周期参激和外激系统的尺度效应开展了一系列工作[23 ,24 ] . 当周期激励频率远小于系统的固有频率时,可以将整个激励项视为慢变参数,从而得到广义自治系统[25 ] ,通过对广义自治系统的平衡态及其分岔行为的分析,进而利用转换相图,得到了多种簇发振荡模式及其相应的分岔机制[26 ] . 这些工作均是针对单项激励开展的,而实际系统往往存在着多种激励共存的现象,因此,开展多种激励联合作用下系统尺度效应的研究有一定的科学价值.
基于此,本文以修正的四维蔡氏电路为基础,通过引入两频率不同的周期电流源,适当取定参数,建立了相对简单的双频激励电路模型. 以此模型为例,给出了各种类型的簇发振荡行为,结合相应的分岔分析,得到了不同类型簇发振荡及其动力学演化机理.
1 数学模型
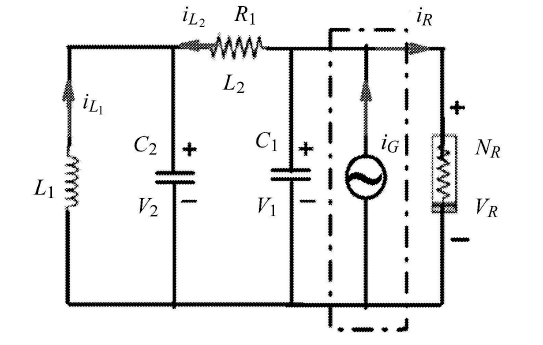
四维修正蔡氏电路中存在着丰富的动力学行 为[27 ] ,在该电路的基础上,引入两频率不同的周期电流源 i G = I G 1 cos ( Ω 1 t ) + I G 2 cos ( Ω 2 t ) 图1 所示,其中非线性阻尼的伏安特性方程为 g ( V 1 ) = Δ 1 V 1 + Δ 2 V 1 3 + Δ 3 V 1 5 Δ 1 Δ 2 Δ 3
$ \left.\!\! \begin{array}{c} d V_1 / d t = \dfrac{1}{C_1 }[G_1 (V_2 - V_1 ) - G_1 g(V_1 ) + i_G ] \\ d V_2 / d t = \dfrac{1}{C_2 }[G_1 (V_1 - V_2 ) + i_{L_1 } + i_{L_2 } ] \\ d i_{L_1 } / d t = -\dfrac{1}{L_1 }(V_2 - R_2 i_{L_2 } ) \\ d i_{L_2 } / d t = - \dfrac{1}{L_2 }V_2 \end{array}\!\!\right\} (1)$
图 1 双频外激励电路模型
Fig. 1 Circuit model with two periodic excitations related to different frequencies
其中 G 1 = 1 / R 1 G 2 = 1 / R 2 . 引入变换 V 1 = E 10 x V 2 = E 20 y i L 1 = E 20 u / R 1 i L 2 = E 20 v / R 1 t = R 1 C 2 τ R 2 = L 1 / R 1 C 2
$ \left.\!\!\begin{array}{c} d x / d \tau = \alpha [y - \delta (x + bx^3 + cx^5)] + w \\ d y / d \tau = \kappa x - y + u + v \\ d u / d \tau = - \gamma y + v \\ d v / d \tau = - \beta y \end{array}\!\!\right\} (2)$
其中, α = C 2 E 20 / C 1 E 10 β = R 1 2 C 2 / L 2 γ = R 1 2 C 2 / L 1 δ = E 10 ( 1 + Δ 1 ) / E 20 κ = E 10 / E 20 b = Δ 2 E 10 2 / ( 1 + Δ 1 ) c = Δ 3 E 10 4 / ( 1 + Δ 1 ) . E 10 E 20 w = A 1 cos ( ω 1 τ ) + A 2 cos ( ω 2 τ ) A 1 = I G 1 R 1 C 2 / C 1 E 10 A 2 = I G 2 R 1 C 2 / C 1 E 10 ω i = Ω i R 1 C 2 ( i = 1 , 2 ) .
当两外激励项不存在时,系统会由平衡点失稳进入周期振荡,进而进入混沌,而对于某些参数条件,存在着对应于两个正Lyapunov指数[28 ] . 周期外激励的存在,同样会导致系统由周期振荡进入混沌. 假设外激励为零,可以计算系统的固有频率,而非线性系统的固有频率与系统的运动状态有关,如当系统逐渐稳定于某一焦点时,其固有频率为该焦点雅可比矩阵的一对共轭复根的虚部值,而当系统表现为周期振荡时,其固有频率为该振荡的频率. 在此取 ω 1 = 0.01 ω 2 = 0.005
2 分岔分析
由于两外激励频率处于严格的共振关系,假设 W = cos ( 0.005 τ ) w = A 1 cos ( ω 1 τ ) + A 2 cos ( ω 2 τ ) = A 1 ( 2 W 2 - 1 ) + A 2 W . 同时,由于激励频率远小于系统的固有频率,因此,可以将 W
$ \left.\!\!\begin{array}{c} d x / d \tau = \alpha [y - \delta (x + bx^3 + cx^5)] + A_1 (2W^2 - 1) + A_2 W \\ d y / d \tau = \kappa x - y + u + v \\ d u / d \tau = - \gamma y + v \\ d v / d \tau = - \beta y \end{array}\!\!\right\} (3) $
而慢子系统为 W = cos ( 0.005 τ ) . 为揭示快慢耦合复杂行为的产生机制,首先分析快子系统的分岔行为. 其平衡点可以表示为 E 0 ( x , y , u , v ) = ( X 0 , 0 , - κ X 0 , 0 ) X 0
- αδ ( X 0 + b X 0 3 + c X 0 5 ) + A 1 ( 2 W 2 - 1 ) + A 2 W = 0 (4)
其相应的特征方程为
λ 4 + h 1 λ 3 + h 2 λ 2 + h 3 λ + h 4 = 0 (5)
式中, h 1 = 1 + αδ Λ h 2 = β + γ - ακ + αδ Λ h 3 = β + αβδ Λ + αγδ Λ h 4 = αβδ Λ Λ = 1 + 3 b X 0 2 + 5 c X 0 4 . 当参数满足 h 1 > 0 h 1 h 2 - h 3 > 0 h 1 h 2 h 3 - h 1 2 h 4 - h 3 2 > 0 h 4 > 0 E 0 h 4 = 0
$ \left.\!\!\begin{array}{l} 1 + 3bX_0^2 + 5cX_0^4 = 0 \\ - \alpha \delta (X_0 + bX_0^3 + cX_0^5 ) + A_1 (2W^2 - 1) + A_2 W = 0 \end{array}\!\! \right \} (6) $
可能会产生fold分岔,导致不同平衡点之间的跳跃. 而当参数满足HB ( h 1 > 0 , h 4 > 0 , h 1 h 2 - h 3 > 0 )
$ h_1 h_2 h_3 - h_1^2 h_4 - h_3^2 = 0 (7)$
则 E 0 Ω H 2 = h 3 / h 1
$ \left.\begin{array}{l} 1 + 3bX_0^2 + 5cX_0^4 = 0 \\ - \alpha \delta (X_0 + bX_0^3 + cX_0^5 ) + A_1 (2W^2 - 1) + A_2 W = 0 \\ \alpha \kappa - \gamma = 0 \end{array}\!\!\right\} (8)$
可能会产生余维二fold-Hopf分岔,导致平衡点向远离该平衡点所在平衡曲线的极限环的跳跃.
固定参数 α = 8.0 β = 0.5 γ = 8.0 δ = 0.15 κ = 0.5 b = - 2.0 c = 1.2 A 2 = 0.2 . 图2 分别给出了 A 1 = 0.2 A 1 = 0.5 A 1 = 2.0 图2 (d)中可以看出,整个外激励项 A 1 ( 2 W 2 - 1 ) + A 2 W W 图2 (a) ~ 图2 (c)中的平衡曲线也不关于 W 图2 (d)中发现,3种不同情形下的整个外激励项变化曲线S 1 2 3 G 1 G 2 图2 (a) ~ 图2 (c)中的平衡曲线得到证实.
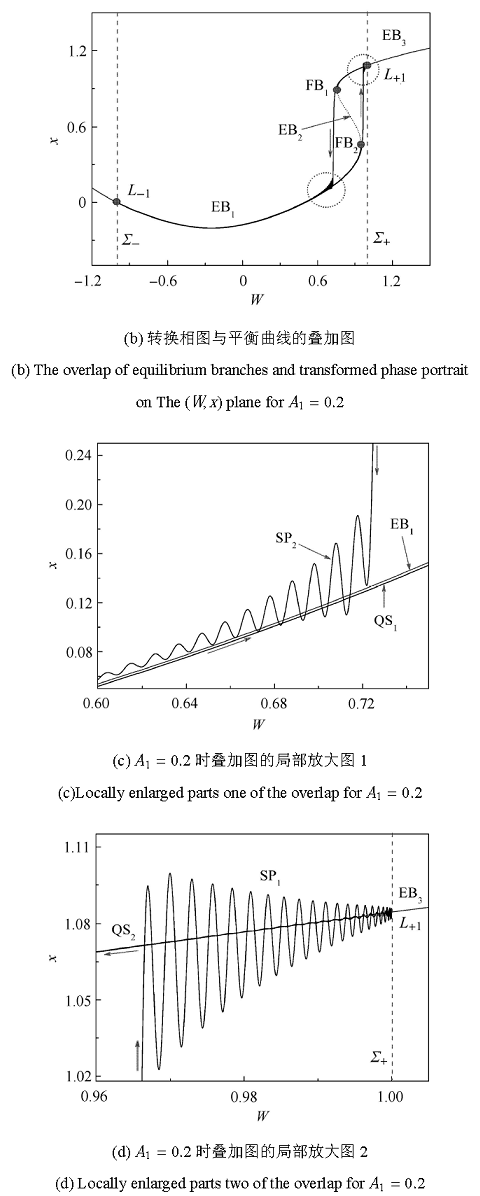
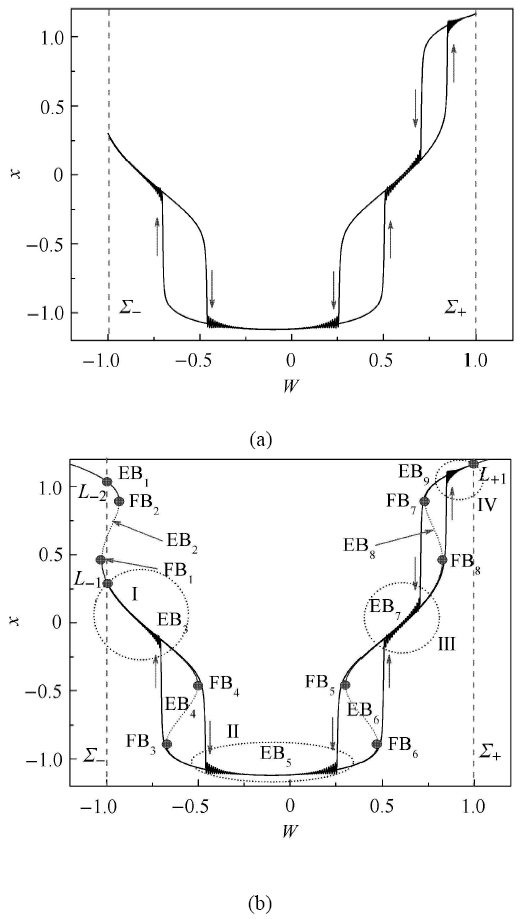
由于 W = cos ( 0.005 τ ) W ∈ [ - 1.0 , + 1.0 ] W W = ± 1.0 Σ ± A 1 = 0.2 图2 (a)可知,平衡曲线由3段组成,其中EB 1 3 2 1 2
图 2 平衡曲线及其分岔图
Fig. 2 The equilibrium branches as well as bifurcation points
随着 A 1 A 1 = 0.5 A 1 = 2.0 W i ( i = 1 , 2 , ⋯ , 9 ) i i i ( i = 1 , 2 , ⋯ , 8 ) 图2 (b)和 图2 (c).
必须指出的是,图2 (b)与图2 (c)的平衡曲线虽然在 W W = - 1.0 W ∈ [ - 1.0 , + 1.0 ] 1 2 3 A 1 = 0.5 A 1 = 2.0
3 尺度效应及其机理分析
由于快子系统不仅决定系统的沉寂态和激发态的形式,同时也决定着它们之间的转化方式,因此3种情形下的平衡曲线及其分岔点的分布会导致系统产生不同的动力学行为,下面我们分别考察其相应的簇发振荡模式及其产生机制.
由于上述的平衡点及分岔分析均是基于将 W W
Π : { [ x ( τ ) , y ( τ ) , u ( τ ) , v ( τ ) ] , ∀ τ ∈ R }
为揭示状态变量与 W
Π G : { [ x ( τ ) , y ( τ ) , u ( τ ) , v ( τ ) , W ( τ ) ] , ∀ τ ∈ R }
其中 W = cos ( 0.005 τ ) W W
3.1 情形一:A1 =0.2
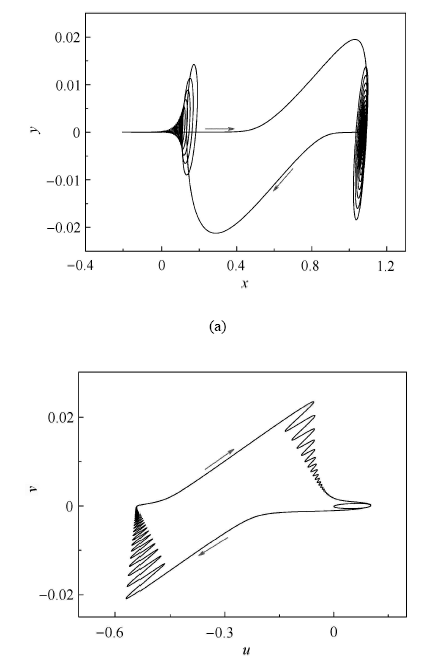
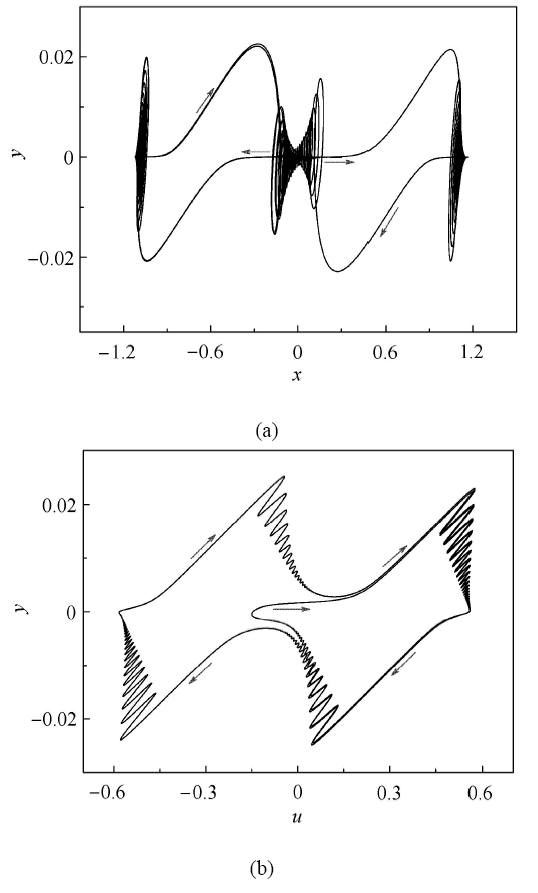
图3 分别给出了 A 1 = 0.2 ( x , y ) ( u , v )
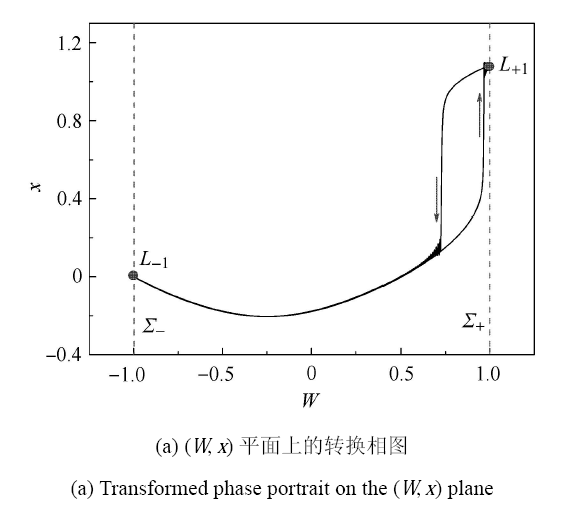
为揭示此振荡的复杂机理,图4 给出了 A 1 = 0.2 ( W , x ) 图4 (a)可以看出,系统轨迹在转换相图上表现为具有滞后环状的周期运动.
假设轨迹从图4 (b)的 L - 1 W W = - 1.0 1 运动, 表现为沉寂态QS1 (参见图4 (c)),
图 3 A 1 = 0.2 ( x , y ) ( u , v )
Fig. 3 Phase portrait for A 1 = 0.2 ( x , y ) ( u , v )
图 4 A 1 = 0.2
Fig. 4 Bursting oscillations for A 1 = 0.2
图 4 A 1 = 0.2
Fig. 4 Bursting oscillations for A 1 = 0.2
直到抵达FB 2 3 3 3 1 ( 参见图4 (d)). 随着 W 3
当 W W = + 1.0 W 3 2 ( 参见图4 (d)),直到轨线抵达FB 1 1 2 ( 参见图4 (c)). 激发态的振荡幅值逐渐减小,直到轨迹稳定于平衡曲线EB 1 1 1 L - 1
显然,簇发振荡的周期与 W 1 3
3.2 情形二:A1 =0.5
增大激励幅值 A 1 A 1 = 0.5 图2 (b)的分岔图可以发现,随 W 图5 给出了 A 1 = 0.5 ( x , y ) ( u , v )
同时,与 A 1 = 0.2 A 1 = 0.5 ( x , y ) ( u , v ) ( x , y ) ( u , v ) ( x , y ) ( u , v )
图 5 A 1 = 0.5 ( x , y ) ( u , v )
Fig. 5 Phase portrait for A 1 = 0.5 ( x , y ) ( u , v )
为揭示其相应的簇发振荡机制,图6 给出了在 ( W , x ) 图4 (a)相比,图6 (a)在 ( W , x )
图 6 A 1 = 0.5 ( W , x )
Fig. 6 (a) Transformed phase portrait on the ( W , x ) ( W , x ) A 1 = 0.5
从图6 (b)可以发现,轨迹在一个周期运动中经历6个fold分岔,分岔点将整个轨迹划分为12段,分别对应着6种沉寂态和6种激发态.
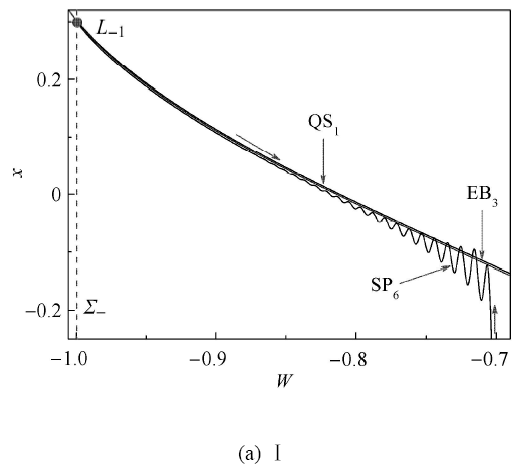
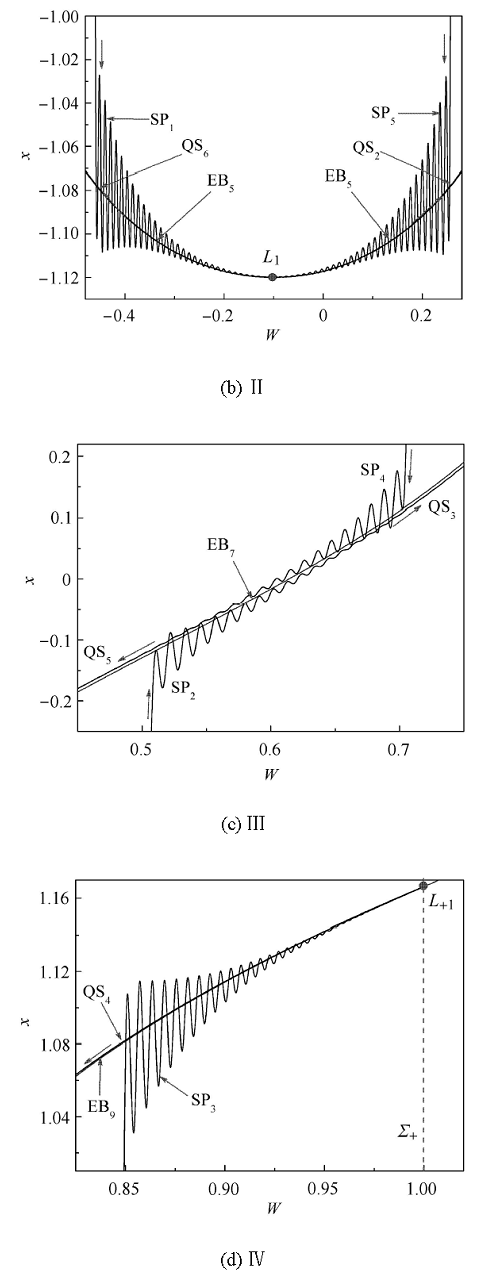
依然假设轨迹从图6 (b)的 L - 1 W W = - 1.0 3 1 ( 参见局部放大图7 (a)),直到抵达FB 4 5 5 5 1 ( 参见局部放大图7 (b)). 随着 W 图7 (b)的 L 1 5 5 2 ( 参见局部放大图7 (b)).
当轨迹沿EB 5 6 7 ( 参见图6 (b)),导致大幅振荡的激发态SP 2 ( 参见局部放大图7 (c)),其振荡幅值逐渐趋向零,导致轨迹几乎严格按照EB 7 3 ( 参见图7 (c)),直到轨迹抵达分岔点FB 8 ( 参见图6 (b)),fold分岔导致跳跃现象,引起轨迹产生围绕稳定平衡曲线EB 9 3 图7 (d)). 随着 W 9 .
图 7 图6 (b)中叠加图Ⅰ,Ⅱ,Ⅲ,Ⅳ处的局部放大图
Fig. 7 Locally enlarged parts Ⅰ,Ⅱ,Ⅲ and Ⅳof the overlapin Fig.6 (b)
图 7 图6 (b)中叠加图Ⅰ,Ⅱ,Ⅲ,Ⅳ处的局部放大图(续)
Fig. 7 Locally enlarged parts Ⅰ,Ⅱ,Ⅲ and Ⅳ of the overlap in Fig.6 (b) (continued)
当 W + 1.0 L + 1 W 9 反向运动,表现为沉寂态QS4 (参见图7 (d)),直到轨线抵达FB7 ,产生fold分岔 (参见图6 (b)),轨迹跳向EB7 ,引起大幅振荡,进入激发态SP4 (参见图7 (c)). 激发态的振荡幅值逐渐减小,直到轨迹稳定于平衡曲线EB7 ,进入沉寂态QS5 (参见图7 (c)),轨迹几乎 严格沿EB7 运动,直到轨迹抵达分岔点FB5 ,fold分岔导致轨迹产生围绕EB5 振荡的激发态SP5 (参见图7 (b)),其振荡幅值在 L 1 5 运动,进入沉寂态QS6 (参见图7 (b)).
当轨迹运行到图6 (b)中的FB3 时,fold分岔使得轨迹跳向稳定平衡曲线EB3 ,产生激发态SP6 (参见图7 (a)). 随着 W 3 上. 当轨迹几乎 严格沿EB3 运动到出发点 L - 1
同样,簇发振荡的周期与 W 3 ,EB5 、EB7 和 EB9 之间由fold分岔来回跳跃,因此该簇发振荡则称为周期6-fold型簇发振荡,其几何结构为点-点-点-点型.
参与振荡的稳定平衡曲线的增加,不仅导致簇发振荡中不同形式沉寂态和激发态数目的变化,也会使得其簇发振荡的结 构在空间中的扩张.
3.3 情形三:A1 =2.0
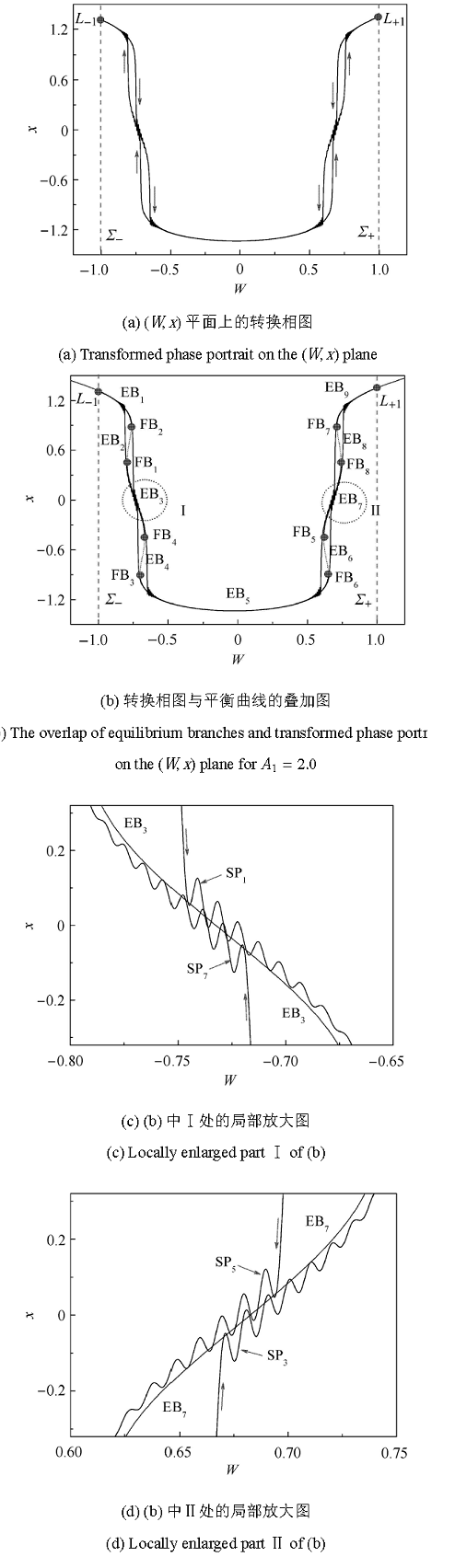
继续增加激励幅值至A1 =2.0,由图2 (c)可知,此时所有稳定平衡曲线及其分岔行为均可能对系统轨迹产生影响, 从而进一步改变簇发振荡的吸引子结构. 图8 分别给出了系统在 ( x , y ) ( u , v )
与图5 中的相图不同,系统轨迹分别在左右两子平面上绕行两圈,但是不是周期倍化行为,这也可以从下文中的转 换相图中得到证实. 比较图5 和图8 中 ( u , v ) A 1 A 1 图8 簇发振荡机制,图9 给出了在 ( W , x )
图 8 A 1 = 2.0 ( x , y ) ( u , v )
Fig. 8 Phase portrait for A 1 = 2.0 ( x , y ) ( u , v )
在慢变参数 W 图9 (a)可知轨迹也会运行一个周期,说明两者之间的周期是一致的. 同时,每一周期内的 轨迹在 ( W , x ) 图9 (b)),从而导致8种相对大幅振荡的激发态,同时,轨迹的激发态均逐渐 收敛于稳定平衡曲线,并几乎严格沿其运动,产生8种沉
图 9 A1 =2.0时的簇发振荡
Fig. 9 Bursting oscillations for A1 =2.0
寂态. 也即该簇发振荡会分别在稳定平衡曲线EB 1 3 5 7 9 A 1 1
同时,从图9 (c)和图9 (d)局部放大图中可以发现,随着 A 1 A 1
4 结 论
对于严格共振的多频激励系统,可以通过适当变换,将所有激励项表示为某一激励项的代数表达. 当激励频率远小于系统的固有频率时,可以将该激励项作为慢变参数,从而建立相应的快子系统和单一慢变量的慢子系统. 通过对快子系统的平衡点及分岔分析,结合转换相图,可以揭示不同簇发振荡的产生机制. 基于相对简单的模型,本文应用上述方法得到了3种典型的簇发振荡,并给出了其相应的产生机制. 由于快子系统的平衡曲线上仅存在fold分岔,发现整个系统的轨线会随参数的不同,沿不同稳定平衡曲线运动,而fold分岔会导致轨迹在不同平衡曲线上的跳跃,产生相应的激发态. 激发态可以用从分岔点向相应稳定平衡曲线的暂态过程来近似,其振荡幅值的变化和振荡频率也可用相应平衡点特征值的实部和虚部来描述. 参与簇发振荡的平衡曲线分岔点越多,其相应簇发振荡吸引子的结构也越复杂.
必须指出的是,当系统中的各激励频率不存在严格共振关系,同时激励频率远小于系统的固有频率时,可以将激励频率与时间之积视为慢变量,同样可以进行相关分析. 在这种情况下,需要一系列的放大图才能将不同簇发振荡的机制描述清楚,我们将另外讨论这种情形.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
Alexandrov DV Bashkirtseva IA Ryashko LB Excitability, mixedmode oscillations and transition to chaos in a stochastic ice ages model
.Physica D , 2017 , 343 (15 ): 28 -37
[本文引用: 1]
[2]
王帅 , 于文浩 , 陈巨辉 等 . 鼓泡流化床中流动特性的多尺度数值模拟
. 力学学报 , 2016 , 48 (1 ): 585 -592
[本文引用: 1]
(Wang Shuai Yu Wenhao Chen Juhui et al .Multi-scale simulation on hydrodynamic characteristics in bubbling fluidized bed
.Chinese Journal of Theoretical and Applied Mechanics , 2016 , 48 (1 ): 585 -592 (in Chinese))
[本文引用: 1]
[3]
Pereda E Dm DLC Mañas S et al .Topography of EEG complexity in human neonates: effect of the postmenstrual age and the sleep state
.Neuroscience Letters , 2006 , 394 (2 ): 152 -157
[本文引用: 1]
[4]
Bi QS The mechanism of bursting phenomena in Belousov- Zhabotinsky (BZ) chemical reaction with multiple time scale
.Sci China-Technol Sci , 2010 , 53 (1 ): 748 -760
[本文引用: 1]
[5]
卓小翔 ,刘辉 ,楚锡华 等 . 非均质材料动力分析的广义多尺度有限元法
. 力学学报 , 2016 , 48 (2 ): 378 -386
[本文引用: 1]
(Zhuo Xiaoxiang Liu Hui Chu Xihua et al .A generalized multiscale finite element method for dynamic analysis of heteroge-neous material
.Chinese Journal of Theoretical and Applied Mechanics , 2016 , 48 (2 ): 378 -386 (in Chinese))
[本文引用: 1]
[6]
Naidu DS Analysis of non-dimensional forms of singular perturbation structures for hypersonic vehicles
.Acta Astronaut , 2010 , 66 (1 ): 577 -586
[本文引用: 1]
[7]
唐宇帆 ,任树伟 ,辛锋先 等 . MEMS 系统中微平板结构声振耦合性能研究
. 力学学报 , 2016 , 48 (4 ): 907 -916
[本文引用: 1]
(Tang Yufan Ren Shuwei Xin Fengxian et al .Scale effect analysis for the vibroacoustic performance of a micro-plate
.Chinese Journal of Theoretical and Applied Mechanics , 2016 , 48 (4 ): 907 -916 (in Chinese))
[本文引用: 1]
[8]
Sánchez AD Izús GG Dell’Erba MG , et al . A reduced gradient description of stochastic-resonant spatiotemporal patterns in a FitzHugh-Nagumo ring with electric inhibitory coupling
.Phys Lett A , 2014 , 378 (22-23 ): 1579 -1583
[本文引用: 1]
[9]
陈章耀 , 张晓芳 , 毕勤胜 . 周期激励下Hartley 模型的簇发及其分岔机制
. 力学学报 , 2010 , 42 (4 ): 765 -773
[本文引用: 1]
(Chen Zhangyao Zhang Xiaofang Bi Qinsheng Bursting phenomena as well as the bifurcation mechanism in periodically excited Hartley model
.Chinese Journal of Theoretical and Applied Mechanics , 2010 , 42 (4 ): 765 -773 (in Chinese))
[本文引用: 1]
[10]
Butera Jr RJ Rinzel J Smith JC Models of respiratory rhythm generation in the pre-Botzinger complex. II. Populations of coupled pacemaker neurons
.J Neurophysiol , 1999 , 82 (1 ): 398 -415
[本文引用: 1]
[11]
Cardin PT Moraes JRD Silva PRD Persistence of periodic orbits with sliding or sewing by singular perturbation
.Journal of Mathematical Analysis and Applications , 2015 , 423 (2 ): 1166 -1182
[本文引用: 1]
[12]
Cao J Huang DS Qu Y Global robust stability of recurrent neural networks
.Chaos Solitons and Fractals , 2004 , 23 (1 ): 221 -229
[本文引用: 1]
[13]
Bear SM Erneux T Rinzel J The slow passage through a Hopf bifurcation: delay, memory effects, and resonance
.SIAM J Appl Math , 1989 , 49 (1 ): 55 -71
[本文引用: 1]
[14]
Ferrari FAS Viana RL Gomez F et al .Macroscopic bursting in physiological networks: node or network property
.New Journal of Physics , 2015 , 17 : 055024
[本文引用: 1]
[15]
Rulkov NF Regularization of synchronized chaotic bursts
.Phys Rev Lett , 2001 ,86 (1 ): 183 -186
[本文引用: 1]
[16]
Wagenaar DA Pine J Potter SM An extremely rich repertoire ofbursting patterns during the development of cortical cultures
.BMC Neurosci , 2006 , 7 (1 ): 1 -18
[本文引用: 1]
[17]
Izhikevich EM Hoppensteadt F Classfication of bursting mapping
.Int J Bifurcat Chaos , 2004 , 14 (11 ): 3847 -3854
[本文引用: 1]
[18]
Simo H Woafo P Bursting oscillations in electromechanical systems
.Mechanics Research Communications , 2011 , 38 (8 ): 537 -547
[本文引用: 1]
[19]
Samoilenko AM Parasyuk IO Repeta BV Dynamical bifurcation of multifrequency oscillations in a fast-slow system
.Ukrainian Mathematical Journal , 2015 , 67 (7 ): 1008 -1037
[本文引用: 1]
[20]
Kingni ST Keuninckx L Woafo P et al .Dissipative chaos,Shilnikov chaos and bursting oscillations in a three-dimensional autonomous system: theory and electronic implementation
. Nonlinear Dyn , 2013 , 73 (1-2 ): 1111 -1123
[本文引用: 1]
[21]
Tanaka H Ushio T Design of bursting in a two-dimensional discrete-time neuron model
.Phys Lett A , 2004 , 350 (1 ): 228 -231
[本文引用: 1]
[22]
张正娣 ,毕勤胜 . 自激作用下洛伦兹振子的簇发现象及其分岔机制
. 中国科学: 物理学力学天文学 , 2013 , 43 (4 ): 511 -517
[本文引用: 1]
(Zhang Zhendi Bi Qinsheng Bursting phenomenon as well as the bifurcation mechanism of self-excited Lorenz system
.Sci Sin-Phys Mech Astron , 2013 , 43 (4 ): 511 -517 (in Chinese))
[本文引用: 1]
[23]
吴天一 ,陈小可 , 张正娣 等 . 非对称型簇发振荡吸引子结构及其机理分析
. 物理学报 , 2017 , 66 (11 ): 35 -45
[本文引用: 1]
(Wu Tianyi Chen Xiaoke Zhang Zhengdi et al .Structures of the asymmetrical bursting oscillation attractors and their bifurcation mechanisms
.Acta Phys Sin , 2017 , 66 (11 ): 35 -45 (in Chinese))
[本文引用: 1]
[24]
张晓芳 ,陈小可 ,毕勤胜 . 快慢耦合振子的张驰簇发及其非光滑分岔机制
. 力学学报 ,2012 , 44 (1 ): 576 -583
[本文引用: 1]
(Zhang Xiaofang Chen Xiaoke Bi Qinsheng Relaxation bursting of a fast-slow coupled oscillation as well as the mechanism of non-smooth bifurcation
.Chinese Journal of Theoretical and Applied Mechanics , 2012 , 44 (1 ): 576 -583 (in Chinese))
[本文引用: 1]
[25]
Han XJ Bi QS Slow passage through canard explosion and mixed mode oscillations in the forced Van der Pol’s equation
.Nonlinear Dyn , 2012 , 68 (1-2 ): 275 -283
[本文引用: 1]
[26]
邢雅清 ,陈小可 ,张正娣 等 . 多平衡态下簇发振荡产生机理及吸引子结构分析
. 物理学报 , 2016 , 65 (9 ): 1 -9
[本文引用: 1]
(Xing Yaqing Chen Xiaoke Zhang Zhengdi et al .Mechanism of bursting oscillations with multiple equilibrium states and the analysis of the structures of the attractors Structures of the asymmetrical bursting oscillation attractors and their bifurcation mechanisms
.Acta Phys Sin , 2016 , 65 (9 ): 1 -9 (in Chinese))
[本文引用: 1]
[27]
Mkaouar H Boubaker O Chaos synchronization for master slave piecewise linear systems: Application to Chua’s circuit
.Communications in Nonlinear Science and Numerical Simulation , 2012 , 17 (1 ): 1292 -1302
[本文引用: 1]
[28]
Dai H Yue X Xie D et al .Chaos and chaotic transients in an aeroelastic system
.Journal of Sound and Vibration , 2014 , 333 (26 ): 7267 -7285
[本文引用: 1]
Excitability, mixedmode oscillations and transition to chaos in a stochastic ice ages model
1
2017
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
鼓泡流化床中流动特性的多尺度数值模拟
1
2016
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
鼓泡流化床中流动特性的多尺度数值模拟
1
2016
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
Topography of EEG complexity in human neonates: effect of the postmenstrual age and the sleep state
1
2006
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
The mechanism of bursting phenomena in Belousov- Zhabotinsky (BZ) chemical reaction with multiple time scale
1
2010
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
非均质材料动力分析的广义多尺度有限元法
1
2016
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
非均质材料动力分析的广义多尺度有限元法
1
2016
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
Analysis of non-dimensional forms of singular perturbation structures for hypersonic vehicles
1
2010
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
MEMS 系统中微平板结构声振耦合性能研究
1
2016
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
MEMS 系统中微平板结构声振耦合性能研究
1
2016
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
A reduced gradient description of stochastic-resonant spatiotemporal patterns in a FitzHugh-Nagumo ring with electric inhibitory coupling
1
2014
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
周期激励下Hartley 模型的簇发及其分岔机制
1
2010
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
周期激励下Hartley 模型的簇发及其分岔机制
1
2010
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
Models of respiratory rhythm generation in the pre-Botzinger complex. II. Populations of coupled pacemaker neurons
1
1999
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
Persistence of periodic orbits with sliding or sewing by singular perturbation
1
2015
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
Global robust stability of recurrent neural networks
1
2004
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
The slow passage through a Hopf bifurcation: delay, memory effects, and resonance
1
1989
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
Macroscopic bursting in physiological networks: node or network property
1
2015
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
Regularization of synchronized chaotic bursts
1
2001
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
An extremely rich repertoire ofbursting patterns during the development of cortical cultures
1
2006
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
Classfication of bursting mapping
1
2004
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
Bursting oscillations in electromechanical systems
1
2011
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
Dynamical bifurcation of multifrequency oscillations in a fast-slow system
1
2015
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
Dissipative chaos,Shilnikov chaos and bursting oscillations in a three-dimensional autonomous system: theory and electronic implementation
1
2013
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
Design of bursting in a two-dimensional discrete-time neuron model
1
2004
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
自激作用下洛伦兹振子的簇发现象及其分岔机制
1
2013
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
自激作用下洛伦兹振子的簇发现象及其分岔机制
1
2013
... 许多工程及科学问题都会涉及到不同尺度之间的耦合[1 ,2 ] . 这些不同尺度可以是时间上的快慢,如在生物细胞中,快速的代谢过程与很慢的遗传变化[3 ] 以及化学反应中存在不同 量级的反应速率[4 ] 等;可以是空间结构上的尺度效应[5 ] ,如飞行器中高速转动和相对低速平动之间的相互作 用[6 ] 以及声振耦合模型中存在的微尺度效应[7 ] 等,也可以是时空尺度混合的[8 ] . 其动力学行为通常会表现为大幅振荡与微幅振荡之间的耦合. 当状态变量处在微幅振荡或几乎不变时,称为沉寂态或静息态(quiescent state, QS),而大幅振荡则称为激发态(spiking state, SP),系统在沉寂态和激发态之间来回变化时,会呈现为簇发振荡[9 ,10 ] 簇发振荡的研究最早可以追溯 到Poincaré研究行星轨迹时建立的奇异方程组[11 ] ,但是直到诺贝尔奖获得者Hodgkin和Huxley建立了两快一慢的 三维模型,成功再现了神经元的簇发放电行为以后,不同尺度耦合系统的复杂行为才受到学术界的广泛关注[12 ,13 ] . 然而,由于缺乏有效 分析方法,相关工作主要围绕 耦合系统的近似求解[14 ] 、数值仿真和实验分析[15 ,16 ] . 2000年,Izhikevich等[17 ] 引入了Rinzel的快慢分析法,才将相关研究提升到机理分析的层次. 其中心思想是,将不同尺度耦合系统分解为相互耦合的快慢两子系统,通过对快子系统的平衡态及其分岔分析,得到沉寂态和激发态之间相互转化的分岔机制,从而揭示相应簇发振荡的产生机理[18 ] . 由于快慢分析法仅对于含有单一慢变量的自治系统有效[19 ,20 ] ,加上高维非线性系统的复杂性,相关工作大多停留在含单慢变量的低维耦合自治系统上[21 ,22 ] . ...
非对称型簇发振荡吸引子结构及其机理分析
1
2017
... 近些年,我们围绕周期参激和外激系统的尺度效应开展了一系列工作[23 ,24 ] . 当周期激励频率远小于系统的固有频率时,可以将整个激励项视为慢变参数,从而得到广义自治系统[25 ] ,通过对广义自治系统的平衡态及其分岔行为的分析,进而利用转换相图,得到了多种簇发振荡模式及其相应的分岔机制[26 ] . 这些工作均是针对单项激励开展的,而实际系统往往存在着多种激励共存的现象,因此,开展多种激励联合作用下系统尺度效应的研究有一定的科学价值. ...
非对称型簇发振荡吸引子结构及其机理分析
1
2017
... 近些年,我们围绕周期参激和外激系统的尺度效应开展了一系列工作[23 ,24 ] . 当周期激励频率远小于系统的固有频率时,可以将整个激励项视为慢变参数,从而得到广义自治系统[25 ] ,通过对广义自治系统的平衡态及其分岔行为的分析,进而利用转换相图,得到了多种簇发振荡模式及其相应的分岔机制[26 ] . 这些工作均是针对单项激励开展的,而实际系统往往存在着多种激励共存的现象,因此,开展多种激励联合作用下系统尺度效应的研究有一定的科学价值. ...
快慢耦合振子的张驰簇发及其非光滑分岔机制
1
2012
... 近些年,我们围绕周期参激和外激系统的尺度效应开展了一系列工作[23 ,24 ] . 当周期激励频率远小于系统的固有频率时,可以将整个激励项视为慢变参数,从而得到广义自治系统[25 ] ,通过对广义自治系统的平衡态及其分岔行为的分析,进而利用转换相图,得到了多种簇发振荡模式及其相应的分岔机制[26 ] . 这些工作均是针对单项激励开展的,而实际系统往往存在着多种激励共存的现象,因此,开展多种激励联合作用下系统尺度效应的研究有一定的科学价值. ...
快慢耦合振子的张驰簇发及其非光滑分岔机制
1
2012
... 近些年,我们围绕周期参激和外激系统的尺度效应开展了一系列工作[23 ,24 ] . 当周期激励频率远小于系统的固有频率时,可以将整个激励项视为慢变参数,从而得到广义自治系统[25 ] ,通过对广义自治系统的平衡态及其分岔行为的分析,进而利用转换相图,得到了多种簇发振荡模式及其相应的分岔机制[26 ] . 这些工作均是针对单项激励开展的,而实际系统往往存在着多种激励共存的现象,因此,开展多种激励联合作用下系统尺度效应的研究有一定的科学价值. ...
Slow passage through canard explosion and mixed mode oscillations in the forced Van der Pol’s equation
1
2012
... 近些年,我们围绕周期参激和外激系统的尺度效应开展了一系列工作[23 ,24 ] . 当周期激励频率远小于系统的固有频率时,可以将整个激励项视为慢变参数,从而得到广义自治系统[25 ] ,通过对广义自治系统的平衡态及其分岔行为的分析,进而利用转换相图,得到了多种簇发振荡模式及其相应的分岔机制[26 ] . 这些工作均是针对单项激励开展的,而实际系统往往存在着多种激励共存的现象,因此,开展多种激励联合作用下系统尺度效应的研究有一定的科学价值. ...
多平衡态下簇发振荡产生机理及吸引子结构分析
1
2016
... 近些年,我们围绕周期参激和外激系统的尺度效应开展了一系列工作[23 ,24 ] . 当周期激励频率远小于系统的固有频率时,可以将整个激励项视为慢变参数,从而得到广义自治系统[25 ] ,通过对广义自治系统的平衡态及其分岔行为的分析,进而利用转换相图,得到了多种簇发振荡模式及其相应的分岔机制[26 ] . 这些工作均是针对单项激励开展的,而实际系统往往存在着多种激励共存的现象,因此,开展多种激励联合作用下系统尺度效应的研究有一定的科学价值. ...
多平衡态下簇发振荡产生机理及吸引子结构分析
1
2016
... 近些年,我们围绕周期参激和外激系统的尺度效应开展了一系列工作[23 ,24 ] . 当周期激励频率远小于系统的固有频率时,可以将整个激励项视为慢变参数,从而得到广义自治系统[25 ] ,通过对广义自治系统的平衡态及其分岔行为的分析,进而利用转换相图,得到了多种簇发振荡模式及其相应的分岔机制[26 ] . 这些工作均是针对单项激励开展的,而实际系统往往存在着多种激励共存的现象,因此,开展多种激励联合作用下系统尺度效应的研究有一定的科学价值. ...
Chaos synchronization for master slave piecewise linear systems: Application to Chua’s circuit
1
2012
... 四维修正蔡氏电路中存在着丰富的动力学行 为[27 ] ,在该电路的基础上,引入两频率不同的周期电流源 i G = I G 1 cos ( Ω 1 t ) + I G 2 cos ( Ω 2 t ) 图1 所示,其中非线性阻尼的伏安特性方程为 g ( V 1 ) = Δ 1 V 1 + Δ 2 V 1 3 + Δ 3 V 1 5 Δ 1 Δ 2 Δ 3
Chaos and chaotic transients in an aeroelastic system
1
2014
... 当两外激励项不存在时,系统会由平衡点失稳进入周期振荡,进而进入混沌,而对于某些参数条件,存在着对应于两个正Lyapunov指数[28 ] . 周期外激励的存在,同样会导致系统由周期振荡进入混沌. 假设外激励为零,可以计算系统的固有频率,而非线性系统的固有频率与系统的运动状态有关,如当系统逐渐稳定于某一焦点时,其固有频率为该焦点雅可比矩阵的一对共轭复根的虚部值,而当系统表现为周期振荡时,其固有频率为该振荡的频率. 在此取 ω 1 = 0.01 ω 2 = 0.005