成层饱和介质平面波斜入射问题的一维化时域方法
ONE-DIMENSIONAL TIME-DOMAIN METHOD FOR FREE FIELD IN LAYERED SATURATED POROELASTIC MEDIA BY PLANE WAVE OBLIQUE INCIDENCE
中图分类号: TU45
通讯作者:
收稿日期: 2017-11-22
接受日期: 2018-02-26
网络出版日期: 2018-02-10
版权声明: 2018 《力学学报》编辑部 《力学学报》编辑部 所有
基金资助:
展开
摘要
地震波斜入射下自由场的输入是大型结构抗震分析中亟待解决的问题之一,尤其是成层饱和多孔介质自由场问题,由于问题的复杂性,目前研究甚少. 本文基于Biot提出的饱和多孔介质动力方程,建立了一种新的求解平面波斜入射下基岩上覆饱和多孔介质成层场地自由场分析的一维化时域计算方法. 该方法首先根据Snell定律将饱和多孔介质二维空间问题转化为一维时域问题,通过对深度方向的有限元离散,得到饱和多孔介质波动问题的一维化有限元方程,然后采用单相弹性介质精确人工边界条件模拟基岩半空间的波动辐射和输入特征,通过考虑基岩与饱和多孔介质间透水或不透水边界条件以及不同饱和多孔介质交界面边界条件,形成基岩上覆成层饱和介质系统的整体有限元方程,最后采用中心差分法与Newmark平均加速度近似格式相结合的方法对时间进行离散,得到节点的动力时程的显式表达. 典型场地的地震反应分析表明,本文方法的计算结果与传递矩阵法结合傅里叶变换的计算结果完全吻合,证明了其有效性.
关键词:
Abstract
The input of free field under oblique incidence of seismic waves is one of the urgent problems to be solved in the seismic analysis of large structures. Because of the complexity of the problem, there are few studies on the free field of layered saturated poroelastic media at present. In this paper, a 1-D time-domain finite element method is proposed to simulate the plane wave motion in layered saturated poroelastic media overlaid on bedrock subjected to the oblique incidence plane wave. The method is on the basis of Biot dynamic theory for saturated poroelastic media. Firstly, the spatially 2-D problem is transformed into a 1-D time-domain problem along the vertical direction according to Snell’s law. 1-D finite element equations for poroelastic media are established by discretization principle and finite element. Then an exact artificial boundary condition for elastic media is used to model the wave absorption and input effects of the truncated bedrock half space. The global finite element equations for the system of layered saturated poroelastic media overlaid on bedrock are developed according to the drained or undrained boundary conditions between the poroelastic medium and the bedrock. By solving the 1D equations, the displacements of nodes in any vertical line can be obtained combining the method of central differences and Average acceleration of Newmark, and the wave motions in layered poroelastic medium system are finally determined based on the characteristic of traveling wave. The method is verified and by comparing with the frequency-domain transfer matrix method with fast Fourier transform in analyzing two engineering site.
Keywords:
引言
地震波输入是目前大型结构抗震分析中亟待解决的问题之一. 以往很多工程的抗震设计中,常假定地震波垂直入射,从而将场地反 应分析简化为一维问题. 而实际上,地震波从震源传播至地表的过程中,因传播路径、地质条件等复杂因素的影响,到达工程场地时并不是垂直 入射的[1,2]. 现有研究表明,不同方向入射波产生的结构反应与垂直入射的结果有明显差别,尤其对于较大尺寸的工程结 构[3,4],如大跨度桥梁、大坝、大型水电站、地下管道和地铁隧道[5]等. 为了确保工程结构在地震作用下的安全性,应考虑地震波斜入射的影响.
近年来,地震波斜入射时场地的地震反应研究取得了很大进展[6]. 以传递矩阵法和刚度矩阵法等方法为代表的频域方法, 基于解析求解,可以得到弹性场地或者非线性场地的等效线性化反应. 目前,已在地震波斜入射时二维成层弹性介质自由场[7,8]以及非线性场地等效线性化[9,10]求解方面 得到广泛应用. 但频域方法无法反应地震过程中土体实际的非线性行为,且其计算精度往往与时域有限元方法不匹配,随着大型结 构--地基系统抗 震分析的发展,建立高精度和实用性强的时域分析方法已经迫在眉睫. 廖河山等[11]用黏性吸收边界条件模拟底层半空间的吸收波效应,基于Snell定律将水平方向 无限的二维空间问题转化 为一维问题,建立了SH波倾斜入射时土层的非线性响应时域分析方法;李山有等[12]基于波动传播水平视波速不变且 已知的特点,利用局部透射边界条件及显式有限差分法的内部节点位移计算公式,给出了地震波斜入射下水平成层半空间自由场 的简化时域计算方法. 刘晶波和王艳[13,14,15]仍采用黏性吸收边界条件来近似模拟截断半空间的吸波效应,在集中质量有限元法和时间中 心差分相结合建立结点运动方程组的基础上,根据Snell定律,将水平方向相邻结点的运动用该结点相邻时刻的运动表示,从而 将水平成层弹性半空间在SH波和P-SV波斜入射下二维自由波场的计算问题简化为时域内的一维问题求解;赵密等[16]在刘 晶波等[14]算法的基础上,提出一种模拟基岩半空间辐射阻尼的人工边界条件代替黏性边界条件,可获得更高的计算精度; 卓卫东等[17]在刘晶波等[14]算法的基础上,建立P-SV波斜入射下有阻尼成层弹性半空间自由波场求解的一维化时域 算法;Zhao等[18]提出一种精确人工边界条件模拟底部半空间的波动辐射和输入特性,并利用Snell定律将水平方向无限的 二维空间问题转化为沿深度方向的一维空间问题,建立了一种计算平面波斜入射下成层半空间自由场地反应的一维化有限元时 域解法.
从这些成果上看,地震波斜入射时场地地震反应的时域分析方法已经得到很大发展,但这些成果都是基于成层单相介质展开的. 实际上地球表面的地震波在从震源通过各种途径传播时,通常要穿过饱和土层和非饱和土层最后到达地面,当将充满液体的土层进 行动力分析时,按饱和多孔介质理论分析比按单相介质理论更为合理. 自1956年Biot[19]建立饱和多孔介质波传播理论至今,人们对于饱和多孔介质层的波动问题已经有了系统深入的认识[20], 但对于地震波斜入射下成层饱和多孔介质自由场地的时域分析研究还处在起步阶段. 王子辉[21]在赵成刚等[22]建立的饱和多孔介质时域显式有限元方法的基础上,采用刘晶波等[14]提出的一维化求解 方法,发展形成了基岩上覆单相固体介质与两相饱和介质互层分布的二维自由波场的一维化时域计算方法. 该方法可用于地震波斜入射下成层饱和多孔介质自由场的计算,但其中,同样采用黏性吸收边界条件来近似模拟基岩的吸波效应,使 得求解精度降低;且因为水平方向也要划分网格,使得有限元离散误差与二维有限元方法一致. 为了克服这些缺点,本文建立了一种新的求解地震波斜入射下基岩上覆饱和多孔介质成层场地自由场分析的一维化时域计算方法. 首先根据Snell定律将饱和多孔介质二维空间问题转化为一维时域问题,通过对深度方向的有限元离散,推导饱和多孔介质一维化有限 元方程,然后基于Zhao等[18]建立了单相弹性介质精确人工边界条件,在考虑基岩与饱和多孔介质间透水或不透水边界条件以 及不同饱和多孔介质交界面边界条件的基础上,形成基岩上覆成层饱和介质系统的整体有限元方程,最后采用中心差分 法与Newmark平均加速度近似格式相结合的方法对时间进行离散,得到节点的动力时程的显式表达. 通过与已有的矩阵传递法的解进行对比,验证了本文方法的有效性.
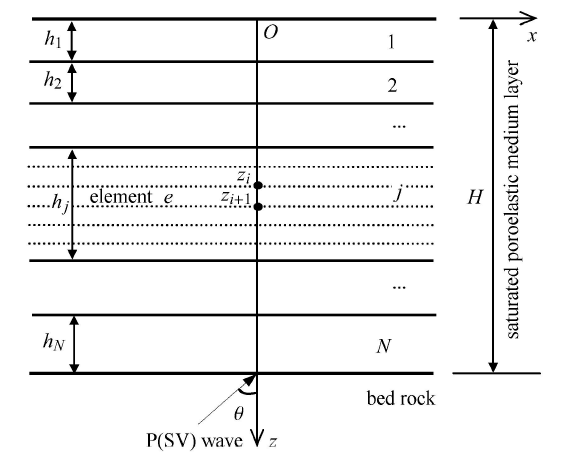
1 成层饱和多孔介质模型
分析模型如图1所示,基岩上覆成层饱和多孔介质,平面P(SV)波从基岩层以
考虑固体颗粒及孔隙 流体的压缩性以及流固两相的惯性耦合和黏性耦合,Biot [19]给出了流体饱和多孔介质的矢量波动方程
$N\nabla ^2{\pmb u}^{\rm s} + \nabla \left[ {\left( {A + N} \right)e + Q\varepsilon } \right] =\rho _{11} \ddot{\pmb u}^{\rm s} + \rho _{12} \ddot{\pmb u}^{\rm f} + b\left( { \dot {\pmb u}^{\rm s} -\dot{\pmb u}^{\rm f}} \right) $(1a)
$\nabla \left[ {Qe + R\varepsilon } \right] = \rho _{12} \ddot {\pmb u}^{\rm s} + \rho _{22} \ddot{\pmb u}^{\rm s} - b\left( {\dot{\pmb u}^{\rm s} - \dot{\pmb u}^{\rm f}} \right) $ (1b)
其中,
$N = \mu $ (2a)
$A = K_{\rm b} - \dfrac{2}{3}\mu + \dfrac{K_{\rm s} ^2}{K_{\rm d} - K_{\rm b} } \left( { 1 -\dfrac{K_{\rm b} }{K_{\rm s} } - n} \right)^2 $ (2b)
$R = \dfrac{n^2K_{\rm s} ^2}{K_{\rm d} - K_{\rm b} }$ (2c)
$Q = n\left(1 - \dfrac{K_{\rm b} }{K_{\rm s} }n\right )\dfrac{K_{\rm s} ^2}{K_{\rm d} - K_{\rm b} } $ (2d)
其中,$K_{\rm d} = K_{\rm s} \left[ {1 + n\left( {\dfrac{K_{\rm s} }{K_{\rm f} } - 1} \right)}\right]$,且
在Biot模型中,固相、液相部分的应力--应变关系分别为
$ \sigma ^{\rm s}_{ij} = 2N\varepsilon _{ij} + \delta _{ij} \left( {Ae + Q\varepsilon } \right) , \ \ \sigma ^{\rm f} = Qe + R\varepsilon (3) $
式中,
基岩视为弹性单相介质,其弹性常数为
2 饱和多孔介质一维化显式有限元方法
一维化方法的关键是根据Snell定理将动力方程中对水平方向的偏导数转化为对时间的导数,将二维平面问题转化为一维时域问题.
2.1 饱和多孔介质波动方程的空间一维化
饱和多孔介质波动方程用矩阵形式表示为[22]
${\bf L}^{\rm T}{\pmb D}_1 {\bf L}{\pmb u}^{\rm s} + {\bf L }^{\rm T}{\pmb D}_2 {\bf L}{\pmb u}^{\rm f} = \rho _{11} \ddot {\pmb u}^{\rm s} + \rho _{12} \ddot{\pmb u}^{\rm f} + b\left( {\dot{\pmb u}^{\rm s} - \dot{\pmb u}^{\rm f}} \right) $ (4a)
${\bf L}^{\rm T}{\pmb D}_2 {\bf L}{\pmb u}^{\rm s} + {\bf L }^{\rm T}{\pmb D}_3 {\bf L}{\pmb u}^{\rm f} = \rho _{12} \ddot {\pmb u}^{\rm s} + \rho _{22} \ddot{\pmb u}^{\rm f} - b\left( {\dot{\pmb u}^{\rm s} - \dot{\pmb u}^{\rm f}} \right) $ (4b)
其中,${\pmb D}_1 $,${\pmb D}_2 $,${\pmb D}_3 $为参数矩阵,表达式分别如下
$\left. \!\!\begin{array}{c}{\pmb D}_1 = \left[ \!\!\begin{array}{ccc} {A + 2N} & A & 0 \\ A & {A + 2N} & 0 \\ 0 & 0 & N \end{array}\!\! \right] \\ {\pmb D}_2 = \left[\!\!\begin{array}{ccc} Q & Q & 0 \\ Q & Q & 0 \\ 0 & 0 & 0 \end{array}\!\! \right] , {\pmb D}_3 = \left[\!\!\begin{array}{ccc} R & R & 0 \\ R & R & 0 \\ 0 & 0 & 0 \end{array} \!\!\right]\end{array}\!\!\right\} (5)$
${\bf L} = \left[\!\! \begin{array}{cc} {\dfrac{\partial }{\partial x}} & 0 \\ 0 & {\dfrac{\partial }{\partial z}} \\ {\dfrac{\partial }{\partial z}} & {\dfrac{\partial }{\partial x}} \end{array} \!\! \right] = \left[\!\!\begin{array}{cc} 1 & 0 \\ 0 & 0 \\ 0 & 1 \end{array} \!\! \right]\dfrac{\partial }{\partial x} + \left[\!\! \begin{array}{cc} 0 & 0 \\ 0 & 1 \\ 1 & 0 \end{array}\!\! \right]\dfrac{\partial }{\partial z} = {\pmb L}_1 \dfrac{\partial }{\partial x} + {\pmb L}_2 \dfrac{\partial }{\partial z}$ (6)
根据Snell定理,水平成层介质水平方向视波速相等,所以有
$ \dfrac{\partial }{\partial x} = - \dfrac{1}{c_x }\dfrac{\partial }{\partial t} (7) $
其中,
$ c_x = \left\{ \!\! \begin{array}{ll} \dfrac{c_{\rm p} }{\sin \theta } , & \hbox{incident P waves} \\ \dfrac{c_{\rm s} }{\sin \beta } , & \hbox{incident SV waves} \end{array}\!\!\right. (8) $
将式(7)代入式(4),得到
$\dfrac{1}{c_x ^2}{\pmb A}_{1} \ddot {\pmb u}^{\rm s} - \dfrac{1}{c_x }({\pmb A}_2 + {\pmb A}_2 ^{\rm T})\dfrac{\partial \dot {\pmb u}^{\rm s}}{\partial z} + {\pmb A}_3 \dfrac{\partial ^2{\pmb u}^{\rm s}}{\partial z^2} +$
$ \dfrac{1}{c_x ^2}{\pmb B}_1 \ddot{\pmb u}^{\rm f} - \dfrac{1}{c_x }({\pmb B }_2 + {\pmb B}_2 ^{\rm T})\dfrac{\partial \dot{\pmb u}^{\rm f}}{\partial z} + {\pmb B }_3 \dfrac{\partial ^2{\pmb u}^{\rm f}}{\partial z^2} =$
$ \rho _{11} \ddot{\pmb u}^{\rm s} + \rho _{12} \ddot{\pmb u}^{\rm f} + b\left( {\dot {\pmb u}^{\rm s} - \dot{\pmb u}^{\rm f}} \right) (9a) $
$ \dfrac{1}{c_x ^2}{\pmb B}_1 \ddot {\pmb u}^{\rm s} - \dfrac{1}{c_x }({\pmb B }_2 + {\pmb B}_2 ^{\rm T})\dfrac{\partial \dot {\pmb u}^{\rm s}}{\partial z} + {\pmb B }_3 \dfrac{\partial ^2 {\pmb u}^{\rm s}}{\partial z^2} +$
$ \dfrac{1}{c_x ^2}{\pmb C }_1 \ddot{\pmb u}^{\rm f} - \dfrac{1}{c_x }({\pmb C }_2 + {\pmb C }_2 ^{\rm T}) \dfrac{\partial \dot{\pmb u}^{\rm f}}{\partial z} + {\pmb C }_3 \dfrac{\partial ^2{\pmb u}^{\rm f}}{\partial z^2} =$
$ \rho _{12} \ddot{\pmb u}^{\rm s} + \rho _{22} \ddot{\pmb u}^{\rm f} - b\left( {\dot{\pmb u}^{\rm s} - \dot{\pmb u}^{\rm f}} \right) $ (9b)
其中
$ \left.\!\!\begin{array}{c} {\pmb A}_1 = {\pmb L}_1 ^{\rm T}{\pmb D}_1 {\pmb L}_1 , \ \ {\pmb A}_2 = {\pmb L}_1 ^{\rm T}{\pmb D}_1 {\pmb L}_2 , \ \ {\pmb A}_3 = {\pmb L}_2 ^{\rm T}{\pmb D}_1 {\pmb L}_2 \\ {\pmb B}_1 = {\pmb L}_1 ^{\rm T}{\pmb D}_2 {\pmb L}_1 , \ \ {\pmb B}_2 = {\pmb L}_1 ^{\rm T}{\pmb D}_2 {\pmb L }_2 , \ \ {\pmb B}_3 = {\pmb L}_2 ^{\rm T}{\pmb D}_2 {\pmb L }_2 \\ {\pmb C }_1 = {\pmb L}_1 ^{\rm T}{\pmb D}_3 {\pmb L}_1 , \ \ {\pmb C }_2 = {\pmb L}_1 ^{\rm T}{\pmb D}_3 {\pmb L }_2 , \ \ {\pmb C }_3 = {\pmb L}_2 ^{\rm T}{\pmb D}_3 {\pmb L}_2 \end{array}\!\!\right\} $
根据式(3),饱和多孔介质中的应力与位移的关系,可以表示为如下的矩阵关系
$ {\pmb \sigma } = \left[ {\sigma _{zz}^{\rm s} \ \ \sigma _{xz}^{\rm s} \ \ \sigma ^{\rm f}} \right]^{\rm T} ={\pmb T }_1 {\pmb u}^{\rm s} +{\pmb T }_2 {\pmb u}^{\rm f} (10) $
其中
$ {\pmb T}_1 = \left[\!\!\begin{array}{cc} {A\dfrac{\partial }{\partial x}} & {(A + 2N)\dfrac{\partial }{\partial z}} \\ {N\dfrac{\partial }{\partial z}} & {N\dfrac{\partial }{\partial x}} \\ {Q\dfrac{\partial }{\partial x}} & {Q\dfrac{\partial }{\partial z}} \end{array}\!\! \right] , \ \ {\pmb T}_2 = \left[\!\!\begin{array}{cc} {Q\dfrac{\partial }{\partial x}} & {Q\dfrac{\partial }{\partial z}} \\ 0 & 0 \\ {R\dfrac{\partial }{\partial x}} & {R\dfrac{\partial }{\partial z}} \end{array} \!\! \right] (11) $
将式(7)代入,得
$ {\pmb \sigma } = \left( { - \dfrac{1}{c_x }{\pmb T}_{11} \dfrac{\partial }{\partial t} + {\pmb T }_{12} \dfrac{\partial }{\partial z}} \right){\pmb u}^{\rm s} + \left( { - \dfrac{1}{c_x }{\pmb T }_{21} \dfrac{\partial }{\partial t} + {\pmb T }_{22} \dfrac{\partial }{\partial z}} \right) {\pmb u}^{\rm f} (12) $
其中
$ \left.\!\!\begin{array}{c} {\pmb T }_{11} = \left[\!\! \begin{array}{cc} A & 0 \\ 0 & N \\ Q & 0 \\ \end{array}\!\! \right] , \ \ {\pmb T }_{12} = \left[\!\! \begin{array}{cc} 0 & {A + 2N} \\ N & 0 \\ 0 & Q \\ \end{array}\!\! \right] \\ {\pmb T }_{21} = \left[\!\! \begin{array}{cc} Q & 0 \\ 0 & 0 \\ R & 0 \\ \end{array}\!\! \right] , \ \ {\pmb T }_{22} = \left[\!\! \begin{array}{cc} 0 & Q \\ 0 & 0 \\ 0 & R \\ \end{array}\!\! \right] \end{array}\!\!\right\} (13)$
2.2 一维化方程的有限元离散
将每一层饱和多孔介质在
${\pmb u}_e^{\rm s} = \left[ {u_{i,x}^{\rm s} } \ \ {u_{i,z}^{\rm s} } \ \ {u_{i + 1,x}^{\rm s} } \ \ {u_{i + 1,z}^{\rm s} } \right]^{\rm T} $ (14a)
${\pmb u}_e^{\rm f} = \left[ {u_{i,x}^{\rm f} } \ \ {u_{i,z}^{\rm f} } \ \ {u_{i + 1,x}^{\rm f} } \ \ {u_{i + 1,z}^{\rm f} } \right]^{\rm T}$ (14b)
令${\pmb u}^{\rm s} = {\pmb N}{\pmb u}_e^{\rm s} $,${\pmb u}^{\rm f} ={\pmb N}{\pmb u}_e^{\rm f} $. 其中,N为形状函数矩阵
$ {\pmb N} = \left[ \begin{array}{cccc} {N_1 } & 0 & {N_2 } & 0 \\ 0 & {N_1 } & 0 & {N_2 } \end{array} \right] (15) $
其中,$N_1 = \dfrac{z_{i + 1} - z}{\Delta z}$,$N_2 = \dfrac{z - z_i }{\Delta z}$.
针对单元e,方程(9)的Galerkin弱式可以写成
${\pmb M}_{\rm s}^e \ddot {\pmb u}_e^{\rm s} +{\pmb M}_{\rm sf }^e \ddot {\pmb u}_e^{\rm f} + {\pmb C}_{\rm s}^e \dot{\pmb u}_e^{\rm s} + {\pmb C}_{\rm sf }^e \dot{\pmb u}_e^{\rm f} + {\pmb K}_{\rm s}^e {\pmb u}_e^{\rm s} + {\pmb K}_{\rm sf }^e {\pmb u}_e^{\rm f} = {\pmb f}_e $ (16a)
${\pmb M}_{\rm fs}^e \ddot{\pmb u}_e^{\rm s} + {\pmb M}_{\rm f}^e \ddot{\pmb u}_e^{\rm f} + {\pmb C}_{\rm fs}^e \dot{\pmb u}_e^{\rm s} + {\pmb C}_{\rm f}^e \dot{\pmb u}_e^{\rm f} + {\pmb K}_{\rm fs}^e {\pmb u}_e^{\rm s} + {\pmb K}_{\rm f}^e {\pmb u}_e^{\rm f} = {\pmb F}_e $ (16b)
其中,${\pmb f}_e $和${\pmb F}_e $为单元载荷列阵,分别为
$ {\pmb f}_e = \left[ {\left. {\sigma _{xz}^{\rm s} } \right|_{z_i } } \ \ {\left. {\sigma_{zz}^{\rm s} } \right|_{z_i } } \ \ {\left. { - \sigma _{xz}^{\rm s} } \right|_{z_{i + 1} } } \ \ {\left. { - \sigma _{zz}^{\rm s} } \right|_{z_{i + 1} } } \right]^{\rm T} (17a)
$
$ {\pmb F}_e = \left[ 0 \ \ {\left. {\sigma ^{\rm f}} \right|_{z_i } } \ \ 0 \ \ {\left. { - \sigma ^{\rm f}} \right|_{z_{i + 1} } } \right]^{\rm T} (17b) $
2.3 组装成整体有限元方程
在同一种饱和多孔介质内部,可以直接对单元有限元离散方程进行组装,对不同饱和多孔介质层之间,需要考虑介质层之间 的边界条件. 下面以两个单元(如图2)为例,说明不同饱和多孔介质层之间有限元离散方程的组装.
假定不同介质层间无相对运动,则不同饱和多孔介质层交界面的边界条件为:
饱和多孔介质骨架法向位移连续
饱和多孔介质骨架切向位移连续
法向相对位移连续
饱和多孔介质骨架切向应力连续
法向总应力连续
孔隙水压力连续
$ \dfrac{1}{n}\sigma ^{\rm f} = \dfrac{1}{{n}'}\sigma ^{\rm f'} (18{\rm f}) $
不同饱和土层,下层饱和土层的各量用上角标“
为了便于应用边界条件,将饱和多孔介质单元的有限元方程式(16)展开为规范化形式
$ \sum_{k = 1}^3 {\sum_{l = 1}^2 {{\pmb A}^e\left( {k,l} \right){\pmb u}^e\left( {k,l} \right)} } = {\pmb f}^{ e} (19a) $
$ \sum_{k = 1}^3 {\sum_{l = 3}^4 {{\pmb A}^e\left( {k,l} \right) {\pmb u}^e\left( {k,l} \right)} } = {\pmb F}^{ e} (19b) $
其中
$ \left. {\pmb A}^e\left( {1,1} \right) = {\pmb M}_{\rm s}^e , {\pmb A}^e\left( {1,2} \right) ={\pmb M}_{\rm sf}^e , {\pmb A}^e\left( {1,3} \right) ={\pmb M}_{\rm fs}^e \\ {\pmb A}^e\left( {1,4} \right) = {\pmb M}_{\rm f}^e , {\pmb A}^e\left( {2,1} \right) = {\pmb C}_{\rm s}^e , {\pmb A}^e\left( {2,2} \right) = {\pmb C}_{\rm sf }^e \\ {\pmb A}^e\left( {2,3} \right) = {\pmb C}_{\rm fs }^e , {\pmb A}^e\left( {2,4} \right) = {\pmb C}_{\rm f}^e , {\pmb A}^e\left( {3,1} \right) = {\pmb K}_{\rm s}^e \\ {\pmb A}^e\left( {3,2} \right) = {\pmb K}_{\rm sf }^e , {\pmb A}^e\left( {3,3} \right) = {\pmb K}_{\rm fs }^e , {\pmb A}^e\left( {3,4} \right) = {\pmb K}_{\rm f}^e \\ {\pmb u}^e\left( {k,l} \right) = {\pmb u}_e^{{\rm s}\left( {3 - k} \right)} \ (l = 1,3) \\ {\pmb u}^e\left( {k,l} \right) = {\pmb u}_e^{\rm f(3-k)} \ (l = 2,4) \!\!\right. $
上标
令
$ {\pmb u}_e^{\rm f} = \dfrac{1}{n_e }{\pmb w}_e + {\pmb u}_e^{\rm s} (20) $
其中,
$ \sum_{k = 1}^3 {\sum_{l = 1}^2 {{\pmb B}^e\left( {k,l} \right) {\pmb U}^e\left( {k,l} \right)} } = {\pmb f}_1^{ e} $ (21a)
$ \sum_{k = 1}^3 {\sum_{l = 3}^4 {{\pmb B}^e\left( {k,l} \right) {\pmb U}^e\left( {k,l} \right)} } = {\pmb f}_2^{ e} $ (21b)
其中
$ {\pmb A}^e\left( {k,l} \right) = \left[ {a_{ij}^e \left( {k,l} \right)} \right] , \ \ {\pmb B}^e\left( {k,l} \right) = \left[ {b_{ij}^e \left( {k,l} \right)} \right] \\ b_{ij}^e \left( {k,1} \right) = \sum_{l = 1}^2 {a_{ij}^e \left( {k,l} \right)} \ \ \left( {i = 1,3} \right) \\ b_{ij}^e \left( {k,1} \right) = \sum_{l = 1}^4 {a_{ij}^e \left( {k,l} \right)} \ \ \left( {i = 2,4} \right) \\ b_{ij}^e \left( {k,2} \right) = \dfrac{1}{n_e }a_{ij}^e \left( {k,2} \right) \ \ \left( {i = 1,3} \right) \\ b_{ij}^e \left( {k,2} \right) = \dfrac{1}{n_e }\left( {a_{ij}^e \left( {k,2} \right) + a_{ij}^e \left( {k,4} \right)} \right) \ \ \left( {i = 2,4} \right) \\ b_{ij}^e \left( {k,3} \right) = \sum_{l = 3}^4 {a_{ij}^e \left( {k,l} \right)} \ \ \left( {i = 1,3} \right) \\ b_{ij}^e \left( {k,3} \right) = \dfrac{1}{n_e }\sum_{l = 3}^4 {a_{ij}^e \left( {k,l} \right)} \ \ \left( {i = 2,4} \right) \\ b_{ij}^e \left( {k,4} \right) = \dfrac{1}{n_e }a_{ij}^e \left( {k,4} \right) \ \ \left( {i = 1,3} \right) \\ b_{ij}^e \left( {k,4} \right) = \dfrac{1}{n_e^2 }a_{ij}^e \left( {k,4} \right) \ \ \left( {i = 2,4} \right) $
$ {\pmb U}^e\left( {k,l} \right) = {\pmb u}_e^{{\rm s}\left( {3 - k} \right)} (l = 1,3) \\ {\pmb U}^e\left( {k,l} \right) = {\pmb w}_e^{ ( 3 - k ) } \ \ (l = 2,4) \\ {\pmb f}_1^e = \left\{ {\left. {\sigma _{xz}^{\rm s} } \right|_{z_e } } \ \ {\left. {\left( {\sigma _{zz}^{\rm s} + \sigma^{\rm f} } \right)} \right|_{z_e } } \ \ {\left. { - \sigma _{xz}^{\rm s} } \right|_{z_{e + 1} } } \ \ {\left. { - \left( {\sigma _{zz}^{\rm s} + \sigma^{\rm f} } \right)} \right|_{z_{e + 1} } } \right\}^{\rm T} \\ {\pmb f}_2^e = \left\{ 0 \ \ {\left. {\dfrac{1}{n_e}\sigma^{\rm f} } \right|_{z_e } } \ \ 0 \ \ {\left. { - \dfrac{1}{n_{e + 1}}\sigma^{\rm f} } \right|_{z_{e + 1} } } \right\}^{\rm T} $
因为不同饱和多孔介质层间切向相对位移不存在连续性条件,进行单元有限元方程叠加时需要进行如下数学处理:在不增加约束条件的前提下在整体位移、速度和加速度列阵中各增加一个维度,并且保证等式的恒成立. 处理后,不同饱和多孔介质层间相关联的两个单元叠后的结果可以表示为
$ \sum_{k = 1}^3 {\sum_{l = 1}^2 {\left( { {\pmb B}\left( {k,l} \right) {\pmb U}\left( {k,l} \right)} \right)} } = {\pmb f}_1 (22a)$
$ \sum_{k = 1}^3 {\sum_{l = 3}^4 {\left( {{\pmb B}\left( {k,l} \right) {\pmb U}\left( {k,l} \right)} \right)} } = {\pmb f}_2 (22b)$
式(22)中
${\pmb B}\left( {k,1} \right) = \left[\!\! \begin{array}{ccccccc} {b_{11}^e \left( {k,1} \right)} & {b_{12}^e \left( {k,1} \right)} & {b_{13}^e \left( {k,1} \right)} & 0 & {b_{14}^e \left( {k,1} \right)} & 0 & 0 \\ {b_{21}^e \left( {k,1} \right)} & {b_{22}^e \left( {k,1} \right)} & {b_{23}^e \left( {k,1} \right)} & 0 & {b_{24}^e \left( {k,1} \right)} & 0 & 0 \\ {b_{31}^e \left( {k,1} \right)} & {b_{32}^e \left( {k,1} \right)} & {b_{33}^e \left( {k,1} \right)} & {b_{11}^{e + 1} \left( {k,1} \right)} & {b_{34}^e \left( {k,1} \right) + b_{12}^{e + 1} \left( {k,1} \right)} & {b_{13}^{e + 1} \left( {k,1} \right)} & {b_{14}^{e + 1} \left( {k,1} \right)} \\ 0 & 0 & 1 & { - 1} & 0 & 0 & 0 \\ {b_{41}^e \left( {k,1} \right)} & {b_{42}^e \left( {k,1} \right)} & {b_{43}^e \left( {k,1} \right)} & {b_{21}^{e + 1} \left( {k,1} \right)} & {b_{44}^e \left( {k,1} \right) + b_{22}^{e + 1} \left( {k,1} \right)} & {b_{23}^{e + 1} \left( {k,1} \right)} & {b_{24}^{e + 1} \left( {k,1} \right)} \\ 0 & 0 & 0 & {b_{31}^{e + 1} \left( {k,1} \right)} & {b_{32}^{e + 1} \left( {k,1} \right)} & {b_{33}^{e + 1} \left( {k,1} \right)} & {b_{34}^{e + 1} \left( {k,1} \right)} \\ 0 & 0 & 0 & {b_{41}^{e + 1} \left( {k,1} \right)} & {b_{42}^{e + 1} \left( {k,1} \right)} & {b_{43}^{e + 1} \left( {k,1} \right)} & {b_{44}^{e + 1} \left( {k,1} \right)} \end{array} \!\! \right]$
${\pmb B}\left( {k,2} \right) = \left[\!\! \begin{array}{ccccccc} {b_{11}^e \left( {k,2} \right)} & {b_{12}^e \left( {k,2} \right)} & {b_{13}^e \left( {k,2} \right)} & 0 & {b_{14}^e \left( {k,2} \right)} & 0 & 0 \\ {b_{21}^e \left( {k,2} \right)} & {b_{22}^e \left( {k,2} \right)} & {b_{23}^e \left( {k,2} \right)} & 0 & {b_{24}^e \left( {k,2} \right)} & 0 & 0 \\ {b_{31}^e \left( {k,2} \right)} & {b_{32}^e \left( {k,2} \right)} & {b_{33}^e \left( {k,2} \right)} & {b_{11}^{e + 1} \left( {k,2} \right)} & {b_{34}^e \left( {k,2} \right) + b_{12}^{e + 1} \left( {k,2} \right)} & {b_{13}^{e + 1} \left( {k,2} \right)} & {b_{14}^{e + 1} \left( {k,2} \right)} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ {b_{41}^e \left( {k,2} \right)} & {b_{42}^e \left( {k,2} \right)} & {b_{43}^e \left( {k,2} \right)} & {b_{21}^{e + 1} \left( {k,2} \right)} & {b_{44}^e \left( {k,2} \right) + b_{22}^{e + 1} \left( {k,2} \right)} & {b_{23}^{e + 1} \left( {k,2} \right)} & {b_{24}^{e + 1} \left( {k,2} \right)} \\ 0 & 0 & 0 & {b_{31}^{e + 1} \left( {k,2} \right)} & {b_{32}^{e + 1} \left( {k,2} \right)} & {b_{33}^{e + 1} \left( {k,2} \right)} & {b_{34}^{e + 1} \left( {k,2} \right)} \\ 0 & 0 & 0 & {b_{41}^{e + 1} \left( {k,2} \right)} & {b_{42}^{e + 1} \left( {k,2} \right)} & {b_{43}^{e + 1} \left( {k,2} \right)} & {b_{44}^{e + 1} \left( {k,2} \right)} \end{array} \!\! \right]$
${\pmb B}\left( {k,l} \right) = \left[ \!\!\begin{array}{ccccccc} {b_{11}^e \left( {k,l} \right)} & {b_{12}^e \left( {k,l} \right)} & {b_{13}^e \left( {k,l} \right)} & 0 & {b_{14}^e \left( {k,l} \right)} & 0 & 0 \\ {b_{21}^e \left( {k,l} \right)} & {b_{22}^e \left( {k,l} \right)} & {b_{23}^e \left( {k,l} \right)} & 0 & {b_{24}^e \left( {k,l} \right)} & 0 & 0 \\ {b_{31}^e \left( {k,l} \right)} & {b_{32}^e \left( {k,l} \right)} & {b_{33}^e \left( {k,l} \right)} & 0 & {b_{34}^e \left( {k,l} \right)} & 0 & 0 \\ 0 & 0 & 0 & {b_{11}^{e + 1} \left( {k,l} \right)} & {b_{12}^{e + 1} \left( {k,l} \right)} & {b_{13}^{e + 1} \left( {k,l} \right)} & {b_{14}^{e + 1} \left( {k,l} \right)} \\ {b_{41}^e \left( {k,l} \right)} & {b_{42}^e \left( {k,l} \right)} & {b_{43}^e \left( {k,l} \right)} & {b_{21}^{e + 1} \left( {k,l} \right)} & {b_{44}^e \left( {k,l} \right) + b_{22}^{e + 1} \left( {k,l} \right)} & {b_{23}^{e + 1} \left( {k,l} \right)} & {b_{24}^{e + 1} \left( {k,l} \right)} \\ 0 & 0 & 0 & {b_{31}^{e + 1} \left( {k,l} \right)} & {b_{32}^{e + 1} \left( {k,l} \right)} & {b_{33}^{e + 1} \left( {k,l} \right)} & {b_{34}^{e + 1} \left( {k,l} \right)} \\ 0 & 0 & 0 & {b_{41}^{e + 1} \left( {k,l} \right)} & {b_{42}^{e + 1} \left( {k,l} \right)} & {b_{43}^{e + 1} \left( {k,l} \right)} & {b_{44}^{e + 1} \left( {k,l} \right)} \end{array} \!\! \right] \ \ (l = 3,4)$
${\pmb U}\left( {k,l} \right) = \left[\!\! \begin{array}{ccccccc} {u_{x,t - 1}^{{\rm s}(3 - k)} } & {u_{z,t - 1}^{{\rm s}(3 - k)} } & {\bar {u}_{x,t}^{{\rm s}(3 - k)} } & {u_{x,t}^{{\rm s}(3 - k)} } & {u_{z,t}^{{\rm s}(3 - k)} } & {u_{x,t + 1}^{{\rm s}(3 - k)} } & {u_{z,t + 1}^{{\rm s}(3 - k)} } \end{array} \!\! \right]^{\rm T} \ \ (l = 1,2)$
${\pmb U}\left( {k,l} \right) = \left[\!\! \begin{array}{ccccccc} {w_{x,t - 1}^{(3 - k)} } & {w_{z,t - 1}^{(3 - k)} } & {\bar {w}_{x,t}^{(3 - k)} } & {w_{x,t}^{(3 - k)} } & {w_{z,t}^{(3 - k)} } & {w_{x,t + 1}^{(3 - k)} } & {w_{z,t + 1}^{(3 - k)} } \end{array} \!\! \right]^{\rm T} \ \ (l = 3,4)$
${\pmb f}_1 = \left[\!\! \begin{array}{ccccccc} {\sigma _{xz,t - 1}^{\rm s} } & {\sigma _{zz,t - 1}^{\rm s} + \sigma _{t - 1}^{\rm f} } & 0 & 0 & 0 & { - \sigma _{xz,t + 1}^{\rm s} } & { - \left( {\sigma _{zz,t + 1}^{\rm s} + \sigma _{t + 1}^{\rm f} } \right)} \end{array} \!\! \right]^{\rm T} $ ,
$f_2^ = \left[\!\! \begin{array}{ccccccc} 0 & {\dfrac{\sigma _{t - 1}^{\rm f} }{n_{t - 1} }} & 0 & 0 & 0 & 0 & { - \dfrac{\sigma _{t + 1}^{\rm f} }{n_{t + 1} }} \end{array} \!\! \right]^{\rm T}$
其中,下标
3 底部人工边界及输入
设波从基岩入射到饱和多孔介质层中,基岩视作单相弹性介质. Zhao等[18]提出了单相弹性介质精确动力人工边界条件
$ {\pmb\sigma}^{\rm j}= - {\pmb S} {\mathop{\bar {\pmb u}}\limits^{\cdot}}^{\rm j} + \left( {{\pmb S} + {\pmb R}} \right) \dot {\hat {\pmb u}}^{\rm j} (23) $
其中,上标“j”表示基岩,
$ {\pmb S} = \dfrac{\rho ^{\rm j}c_{\rm s} }{m_{\rm p} m_{\rm s} + n_{\rm p} n_{\rm s} }\cdot \\ \left[ \!\!\begin{array}{cc} {n_{\rm p} } & {2n_{\rm s} n_{\rm p} m_{\rm s} - m_{\rm p} \left( {1 - 2m_{\rm s}^{2} } \right)} \\ {m_{\rm p} \left( {1 - 2m_{\rm s}^{2} } \right) - 2n_{\rm s} n_{\rm p} m_{\rm s} } & {m_{\rm p} n_{\rm s} / m_{\rm s} } \end{array}\!\!\right] \\ {\pmb R} = \rho ^{\rm j}c_{\rm s} \left[\!\! \begin{array}{cc} {\left( {1 - 2m_{\rm s}^{2} } \right)n_{\rm s} } & {\left( {1 - 2m_{\rm s}^{2} } \right)m_{\rm s} } \\ {2m_{\rm s} n_{\rm s}^{2} } & {2m_{\rm s}^{2} n_{\rm s} } \end{array} \!\! \right] \\ m_{\rm p} = \dfrac{c_{\rm p} }{c_x } , \ \ n_{\rm p} = \sqrt {1 - m_{\rm p}^2 } , \ \ m_{\rm s} = \dfrac{c_{\rm s} }{c_x } , \ \ n_{\rm s} = \sqrt {1 - m_{\rm s}^{2} } $
基岩层与第
法向位移连续
切向位移连续
切向应力连续
法向总应力连续
当基岩透水时,孔隙水压力为零
$ p_{\rm f} = -\dfrac 1n \sigma^{\rm f} =0 (24e) $
当基岩不透水时,饱和多孔介质土骨架和液相法向位移相等
根据基岩层与第
当基岩边界透水时
$ \left. \!\! \begin{array}{l} {\pmb M}_{\rm s} \ddot {\pmb u}_1 + {\pmb M}_{\rm sf } \ddot {\pmb u}_2 + {\pmb C}'_{\rm s} \dot {\pmb u}_1 + {\pmb C}_{\rm sf} \dot{\pmb u}_2 + {\pmb K}_{\rm s} {\pmb u}_1 + {\pmb K}_{\rm sf } {\pmb u}_2 = {\pmb F}_1 \\ {\pmb M}_{\rm fs} \ddot{\pmb u}_1 + {\pmb M}_{\rm f} \ddot {\pmb u}_2 + {\pmb C}_{\rm fs } \dot {\pmb u}_1 + {\pmb C}_{\rm f} \dot{\pmb u}_2 + {\pmb K}_{\rm fs} {\pmb u}_1 + {\pmb K}_{\rm f} {\pmb u}_2 = {\pmb F}_2 \end{array} \!\! \right \} (25) $
其中,${\pmb C}'_{\rm s} = {\pmb C}_{\rm s} + {\pmb C}_{\rm B} $,且${\pmb C}_{\rm B} = \left[ \!\! \begin{array}{cccc} 0 & \cdots & \cdots & 0 \\ \vdots & \ddots & & \vdots \\ \vdots & & 0 & 0 \\ 0 & \cdots & 0 & { - {\pmb S}} \end{array}\!\! \right]$;${\pmb M}_{\rm s} $,${\pmb M}_{\rm sf} $,${\pmb M}_{\rm f} $,${\pmb M}_{\rm fs} $为整体质量矩阵,${\pmb C}_{\rm s} $,${\pmb C}_{\rm sf} $,${\pmb C}_{\rm f} $, ${\pmb C}_{\rm fs}$为整体阻尼矩阵,${\pmb K}_{\rm s} $,${\pmb K}_{\rm sf} $,${\pmb K}_{\rm f} $,${\pmb K}_{\rm fs} $为整体刚度矩阵,按式(22)的方式组装;${\pmb u}_1 $和${\pmb u}_2 $为整体位移列阵
$ {\pmb u}_1 = \Big \{ {u_{1x}^{\rm s} } \ \ {u_{1z}^{\rm s} } \ \ \cdots \ \ {u_{t - 1x}^{\rm s} } \ \ {u_{t - 1z}^{\rm s} } \ \ {\bar {u}_{tx}^{\rm s} } \ \ {u_{tx}^{\rm s} } \ \ {u_{tz}^{\rm s} } \ \ {u_{t + 1x}^{\rm s} } \ \ {u_{t + 1z}^{\rm s} } \ \ \cdots \ \ {u_{nx}^{\rm s} } \ \ {u_{nz}^{\rm s} } \Big \}^{\rm T} $
$ {\pmb u}_2 = \Big\{ {w_{1x} } \ \ {w_{1z} } \ \ \cdots \ \ {w_{t - 1x} } \ \ {w_{t - 1z} } \ \ {\bar {w}_{tx} } \ \ {w_{tx} } \ \ {w_{tz} } \ \ {w_{t + 1x} } {w_{t + 1z} } \ \ \cdots \ \ {w_{nx} } \ \ {w_{nz} } \Big \}^{\rm T} $
下标
$ \left. \begin{align}{\pmb F}_1 = \left\{ 0 \ \ \cdots \ \ 0 \ \ { - \left( {{\pmb S} + {\pmb R }} \right)\dot {\hat {u}}^{\rm j}} \right\}^{\rm T} \\ {\pmb F}_2 = \left\{ 0 \ \ \cdots \ \ 0 \right\}^{\rm T}\end{align}\right\} $
P波入射时
$ \dot {\hat {\pmb u}}^{\rm j} = [\sin \theta \ \ - \cos \theta ]^{\rm T} \dot {u}_0 (26) $
SV波入射时
$ \dot {\hat {\pmb u}}^{\rm j} = [\cos \beta \ \ \sin \beta ]^{\rm T}\dot {u}_0 (26) $
当基岩边界不透水时
$ \left.\!\!\begin{align} {M}_{\rm s} \ddot{\pmb u}_1 + {\pmb M}'_{\rm sf} {\ddot {\pmb u}}'_2 + {\pmb C}'_{\rm s} \dot{\pmb u}_1 + {\pmb C}'_{\rm sf} \dot{\pmb u}_2 +{\pmb K}_{\rm s} {\pmb u}_1 + {\pmb K}'_{\rm sf} {\pmb u}_2 = {\pmb F}_1 \\ {\pmb M}_{\rm fs} \ddot{\pmb u}_1 + {\pmb M}'_{\rm f} {\ddot{\pmb u}}'_2 + {\pmb C}_{\rm fs} \dot{\pmb u}_1 + {\pmb C}'_{\rm f} \dot{\pmb u}_2 + {\pmb K}_{{\rm fs}} {\pmb u}_1 + {\pmb K}'_{\rm f} {\pmb u}_2 = {\pmb F}_2 \end{align} \!\! \right\} (27) $
其中
${\pmb M}'_{\rm sf} = \left[\!\!\begin{array}{cccc} {M_{\rm sf} \left( {1,1} \right)} & \cdots & {M_{\rm sf} \left( {1,s - 1} \right)} & 0 \\ \vdots & \ddots & \vdots & \vdots \\ {M_{\rm sf} \left( {s,1} \right)} & \cdots & {M_{\rm sf} \left( {s,s - 1} \right)} & 0 \end{array} \!\! \right]$
${\pmb M}'_{\rm f} = \left[\!\! \begin{array}{cccc} {M_{\rm f} \left( {1,1} \right)} & \cdots & {M_{\rm f} \left( {1,s - 1} \right)} & 0 \\ \vdots & \ddots & \vdots & \vdots \\ {M_{\rm f} \left( {s - 1,1} \right)} & & {M_{\rm f} \left( {s - 1,s - 1} \right)} & 0 \\ {M_{\rm f} \left( {s,1} \right)} & \cdots & {M_{\rm f} \left( {s,s - 1} \right)} & 1 \end{array} \!\! \right]$
${\pmb C}'_{\rm sf} = \left[\!\! \begin{array}{cccc} {C_{\rm sf} \left( {1,1} \right)} & \cdots & {C_{\rm sf} \left( {1,s - 1} \right)} & 0 \\ \vdots & \ddots & \vdots & \vdots \\ {C_{\rm sf} \left( {s,1} \right)} & \cdots & {C_{\rm sf} \left( {s,s - 1} \right)} & 0 \end{array} \!\! \right]$
${\pmb C}'_{\rm f} = \left[\!\!\begin{array}{cccc} {C_{\rm f} \left( {1,1} \right)} & \cdots & {C_{\rm f} \left( {1,s - 1} \right)} & 0 \\ \vdots & \ddots & \vdots & \vdots \\ {C_{\rm f} \left( {s,1} \right)} & \cdots & {C_{\rm f} \left( {s,s - 1} \right)} & 0 \end{array} \!\! \right]$
${\pmb K}'_{\rm sf} = \left[\!\!\begin{array}{cccc} {K_{\rm sf} \left( {1,1} \right)} & \cdots & {K_{\rm sf} \left( {1,s - 1} \right)} & 0 \\ \vdots & \ddots & \vdots & \vdots \\ {K_{\rm sf} \left( {s,1} \right)} & \cdots & {K_{\rm sf} \left( {s,s - 1} \right)} & 0 \end{array} \!\!\right]$
${\pmb K}'_{\rm f} = \left[\!\! \begin{array}{cccc} {K_{\rm f} \left( {1,1} \right)} & \cdots & {K_{\rm f} \left( {1,s - 1} \right)} & 0 \\ \vdots & \ddots & \vdots & \vdots \\ {C_{\rm f} \left( {s,1} \right)} & \cdots & {K_{\rm f} \left( {s,s - 1} \right)} & 0 \end{array} \!\! \right]$
${\pmb K}'_{\rm sf} = \left[\!\!\begin{array}{cccc} {K_{\rm sf} \left( {1,1} \right)} & \cdots & {K_{\rm sf} \left( {1,s - 1} \right)} & 0 \\ \vdots & \ddots & \vdots & \vdots \\ {K_{\rm sf} \left( {s,1} \right)} & \cdots & {K_{\rm sf} \left( {s,s - 1} \right)} & 0 \end{array} \!\! \right]$
s为整体系数矩阵的总阶次;$\ddot {\pmb u}'_2 = \Big\{ {\ddot {w}_{1x} } \ \ {\ddot {w}_{1z} } \ \ \cdots \ \ {\ddot {w}_{t - 1x} }$ $ {\ddot {w}_{t - 1z} } \ \ {\mathop{\bar {w}}\limits^{\cdot\cdot}}_{tx} \ \ {\ddot {w}_{tx} } \ \ {\ddot {w}_{tz} } \ \ {\ddot {w}_{t + 1x} } \ \ {\ddot {w}_{t + 1z} } \ \ \cdots \ \ {\ddot {w}_{nx} } \ \ {p_{{\rm f}n} } \Big\} ^{\rm T}$, $p_{{\rm f}n} $为饱和多孔介质层与基岩交界面面节点的孔隙水压力.
4 节点动力反应的显式表达
利用一维化的方法建立离散的有限元方程式(25)或式(27)之后,可采用中心差分法与Newmark平均加速度法相结合的显式积分方法求解各节点的动力时程[22] 周正华等[24]和王进廷等[25]先后对比分析了几种常用显式积分方法的稳定性和精度,证明该方法具有二阶精度及良好的稳定性,并给出了其稳定性条件. 李亮等[26]研究了采用该方法进行饱和两相介质波动问题分析时的稳定性影响因素,包括时间步长、空间步距和渗透系数取值等的作用规律. 在此不再赘述.
以基岩透水为例,可以得到用前一时刻的位移和速度表示的当前时刻的位移
$ {\pmb u}_1^{p + 1} = {\pmb u}_1^p + \Delta t\dot{\pmb u}_1^p - \dfrac{\Delta t^2}{2}\left( {{\pmb M}_{\rm f} {\pmb M}_{\rm s} - {\pmb M}_{\rm sf} {\pmb M}_{\rm fs} } \right)^{ - 1} \cdot \\ \Big[ \left( {{\pmb M}_{\rm f} {\pmb C}'_{\rm s} - {\pmb M}_{\rm sf} {\pmb C}_{\rm fs} } \right)\dot{\pmb u}_1^p + \left( {{\pmb M}_{\rm f} {\pmb C}_{\rm sf} - {\pmb M}_{\rm sf} {\pmb C}_{\rm f} } \right)\dot{\pmb u}_2^p + \\ \left( {{\pmb M}_{\rm f} {\pmb K}_{\rm s} - {\pmb M}_{\rm sf} {\pmb K}_{\rm fs} } \right){\pmb u}_1^p + \left( {{\pmb M}_{\rm f} {\pmb K}_{\rm sf} - {\pmb M}_{\rm sf} {\pmb K}_{\rm f} } \right){\pmb u}_2^p - \\ {\pmb M}_{\rm f} {\pmb F}_1^p + {\pmb M}_{\rm sf} {\pmb F}_2^p \Big ] (28a)$
$ {\pmb u}_2^{p + 1} = {\pmb u}_2^p + \Delta t\dot{\pmb u}_2^p - \dfrac{\Delta t^2}{2}\left( {{\pmb M}_{\rm s} {\pmb M}_{\rm f} - {\pmb M}_{\rm fs} {\pmb M}_{\rm sf} } \right)^{ - 1} \cdot \\ \Big[ \left( {{\pmb M}_{\rm s} {\pmb C}_{\rm fs} - {\pmb M}_{\rm fs} {\pmb C}'_{\rm s} } \right)\dot {\pmb u}_1^p + \left( {{\pmb M}_{\rm s} {\pmb C}_{\rm f} - {\pmb M}_{\rm fs} {\pmb C}_{\rm sf} } \right)\dot {\pmb u}_2^p + \\ \left( {{\pmb M}_{\rm s} {\pmb K}_{\rm fs} - {\pmb M}_{\rm fs} {\pmb K}_{\rm s} } \right) {\pmb u}_1^p + \left( {{\pmb M}_{\rm s} {\pmb K}_{\rm f} - {\pmb M}_{\rm fs} {\pmb K}_{\rm sf} } \right) {\pmb u}_2^p - \\ {\pmb M}_{\rm s} {\pmb F}_2^p + {\pmb M}_{\rm fs} {\pmb F}_1^p \Big ] (28b)$
用前一时刻的位移和速度以及当前时刻的位移表示的当前时刻的速度
$ \dot {\pmb u}_1^{p + 1} = \dot{\pmb u}_1^p - \left( { {\pmb M}_{\rm f} {\pmb M}_{\rm s} - {\pmb M}_{\rm sf} {\pmb M}_{\rm fs} } \right)^{ - 1} \cdot \\ \Bigg \{ \left( {{\pmb M}_{\rm f} {\pmb C}'_{\rm s} - {\pmb M}_{\rm sf} {\pmb C}_{\rm fs} } \right)\left( {{\pmb u}_1^{p + 1} - {\pmb u}_1^p } \right) + {\pmb M}_{\rm f} {\pmb C}_{\rm sf} \left( {{\pmb u}_2^{p + 1} - {\pmb u}_2^p } \right) - \\ {\pmb M}_{\rm sf} {\pmb C}_{\rm f} \left( {{\pmb u}_2^{p + 1} - {\pmb u}_2^p } \right) + \dfrac{\Delta t}{2}\left( {{\pmb M}_{\rm f} {\pmb K}_{\rm s} - {\pmb M}_{\rm sf} {\pmb K}_{\rm fs} } \right)\left( {{\pmb u}_1^{p + 1} + {\pmb u}_1^p } \right) + \\ \dfrac{\Delta t}{2}\left( {{\pmb M}_{\rm f} {\pmb K}_{\rm sf} - {\pmb M}_{\rm sf} {\pmb K}_{\rm f} } \right)\left( {{\pmb u}_2^{p + 1} + {\pmb u}_2^p } \right)- \\ \dfrac{\Delta t}{2}\left[ {{\pmb M}_{\rm f} \left( {{\pmb F}_1^{p + 1} + {\pmb F}_1^p } \right) - {\pmb M}_{\rm sf} \left( {{\pmb F}_2^{p + 1} + {\pmb F}_2^p } \right)} \right] \Bigg \} (29a)$
$ \dot{\pmb u}_2^{p + 1} = \dot{\pmb u}_2^p - \left( {{\pmb M}_{\rm s} {\pmb M}_{\rm f} - {\pmb M}_{\rm fs} {\pmb M}_{\rm sf} } \right)^{ - 1} \cdot \\ \Bigg \{ \left( {{\pmb M}_{\rm s} {\pmb C}_{\rm fs} - {\pmb M}_{\rm fs} {\pmb C}'_{\rm s} } \right)\left( {{\pmb u}_1^{p + 1} - {\pmb u}_1^p } \right) + {\pmb M}_{\rm s} {\pmb C}_{\rm f} \left( {{\pmb u}_2^{p + 1} - {\pmb u}_2^p } \right) - \\ {\pmb M}_{\rm fs} {\pmb C}_{\rm sf} \left( {{\pmb u}_2^{p + 1} - {\pmb u}_2^p } \right) + \dfrac{\Delta t}{2}\left( {{\pmb M}_{\rm s} {\pmb K}_{\rm fs} - {\pmb M}_{\rm fs} {\pmb K}_{\rm s} } \right)\left( {{\pmb u}_1^{p + 1} + {\pmb u}_1^p } \right) + \\ \dfrac{\Delta t}{2}\left( {{\pmb M}_{\rm s} {\pmb K}_{\rm f} - {\pmb M}_{\rm fs} {\pmb K}_{\rm sf} } \right)\left( {{\pmb u}_2^{p + 1} + {\pmb u}_2^p } \right) - \\ \dfrac{\Delta t}{2}\left[ {{\pmb M}_{\rm s} \left( {{\pmb F}_2^{p + 1} +{\pmb F}_2^p } \right) - {\pmb M}_{\rm fs} \left( {{\pmb F}_1^{p + 1} +{\pmb F}_1^p } \right)} \right] \Bigg \} (29b)$
由前一时刻的速度和加速度以及当前时刻的速度表示的此时刻的加速度
$\ddot {\pmb u}_1^{p + 1} = - \ddot{\pmb u}_1^p + \dfrac{2}{\Delta t}\left( {\dot{\pmb u}_1^{p + 1} - \dot{\pmb u}_1^p } \right) (30a)$
$\ddot{\pmb u}_2^{p + 1} = - \ddot{\pmb u}_2^p + \dfrac{2}{\Delta t}\left({\dot{\pmb u}_2^{p + 1} - \dot{\pmb u}_2^p } \right) (30b)$
对于应力,按照传统有限元法,单元为常应力单元. 为了提高应力结果的精度,可以采用如下两种方法计算. 其一,采用单元离散方程(21)求解;其二,由式(12)求解,具体表达式如下
$\sigma _{zz}^{\rm s} = - \dfrac{1}{c_x }A\dot {u}_x^{\rm s} + \left( {A + 2N} \right)\dfrac{\partial u_z^{\rm s} }{\partial z} - \dfrac{1}{c_x }Q\dot {u}_x^{\rm f} + Q\dfrac{\partial u_z^{\rm f} }{\partial z} (31a)$
$\sigma ^{\rm f} = - \dfrac{1}{c_x }Q\dot {u}_x^{\rm s} + Q\dfrac{\partial u_z^{\rm s} }{\partial z} - \dfrac{1}{c_x }R\dot {u}_x^{\rm f} + R\dfrac{\partial u_z^{\rm f} }{\partial z} (31b)$
$\sigma _{xz}^s = N\left( {\dfrac{\partial u_x^s }{\partial z} - \dfrac{1}{c_x }\dot {u}_z^s } \right) (31c) $
对于
$ \sigma _{xx}^{\rm s} = \dfrac{AR - Q^2}{\left( {A + 2N} \right)R - Q^2}\sigma _{zz}^{\rm s} + \dfrac{2NQ}{\left( {A + 2N} \right)R - Q^2}\sigma^{\rm f} + \\ \dfrac{4N\left[ {Q^2 - \left( {A + N} \right)R} \right]}{c_x \left[ {\left( {A + 2N} \right)R - Q^2} \right]}\dot {u}_x^{\rm s} (32)$
5 验 证
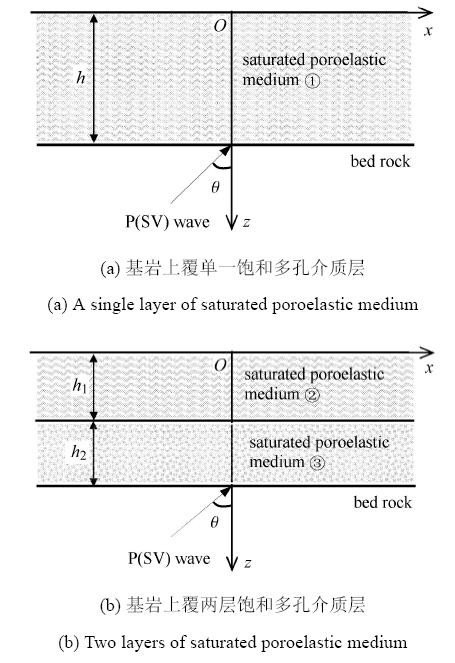
为验证本文方法,采用如图3所示的2个不同场地模型计算,将计算结果与传递矩阵法结合傅里叶变换的计算结果进行对比. 其中图3(a)为基岩上覆单一饱和多孔介质层,图3(b)为基岩上覆两层不同饱和多孔介质层. 基岩层和饱和介质层参数如表1和表2所示. 考虑基岩与饱和介质层交界面为透水边界.
图3 饱和多孔介质覆盖层场地简化模型
Fig. 3 The simplified model of saturated soil overburden site
5.1 地震波输入
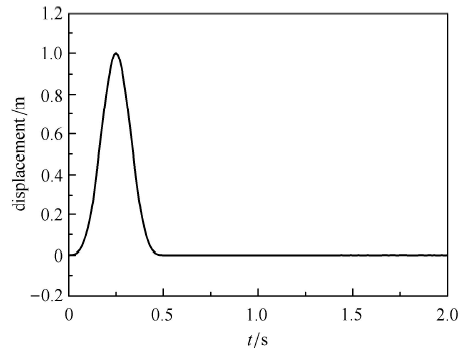
入射波的位移时程采用狄拉克函数的有限差分近似,即
$ u_0 \left( t \right) = 16A\Bigg [ G\left( \tau \right) - 4G\left( {\tau - \dfrac{1}{4}} \right) + 6G\left( {\tau - \dfrac{1}{2}} \right) - 4G\left( {\tau - \dfrac{3}{4}} \right) + G\left( {\tau - 1} \right) \Bigg] (33) $
其中,$G\left( \tau \right) = \tau ^3H\left( \tau \right)$,$\tau =\dfrac{t}{T}$,
5.2 基岩上覆单一饱和多孔介质层
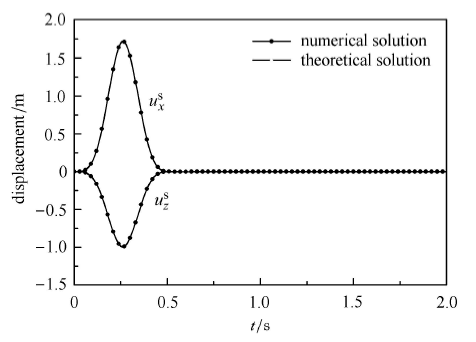
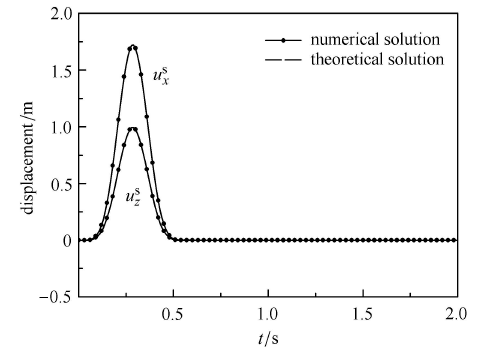
在图3(a)所示的模型中,取饱和多孔介质覆盖层厚度h=100 m,饱和多孔介质取表2中第①组参数,网格厚度取1 m,时间步长取10-4s. 图5和图6分别给出采用本文方法得到的P波60°入射和SV波30°入射时半空间表面O点的固体骨架位移时程. 由于本算例中所取饱和多孔介质参数特殊,孔隙率较小,固体骨架刚度与基岩刚度相同,且大于孔隙流体体积模量,因此此时的饱和多孔介质可以看作和基岩材料相近的单相介质[27],基岩上覆单一饱和多孔介质层模型相应地也可以看成是均匀半空间场地,图中的精确解是根据波传播理论得到的半空间场地地表位移的解析解[28,29]. 从图中可以看出,本文方法的计算结果与解析解完全吻合. 一方面说明本文方法在模拟基岩上覆单一饱和多孔介质层场地时的有效性和精度,另一方面也再次证明,当孔隙率较小,固体骨架刚度大于孔隙流体体积模量时,饱和多孔介质可以作为单相介质处理.
图5 模型一P波60°入射时半空间表面
Fig. 5 Time history of solid phase displacement for point O on the half-space surface excited by P waves with incident angle 60°for model one
图6 模型一SV波30°入射时半空间表面
Fig. 6 Time history of solid phase displacement for point O on the half-space surface excited by SV waves with incident angle 30° for model one
5.3 基岩上覆两层不同饱和多孔介质层
计算模型如图3(b)所示,两层不同饱和介质层的参数分别取表2中第②、③组参数,两层饱和介质层厚度h1=h2=50m,网 格厚度取1 m,时间步长取10-4s. 图7给出了P波60°入射时半空间表面
图7 模型二P波60°入射时半空间表面O点固相位移时程点固相位移时程
Fig. 7 Time history of solid phase displacement for point O on the half-space surface excited by P waves with incident angle 60° for model two
图8 模型二SV波30°入射时半空间表面
Fig. 8 Time history of solid phase displacement for point
6 结 语
本文以Biot流体饱和介质动力方程为基础,根据Snell定律,并结合不同介质交界面的边界条件以及单相弹性介质精确人工边界条件,建立了一种求解地震波斜入射下基岩上覆饱和多孔介质成层场地自由场分析的一维化时域计算方法. 该方法可以方便地求出平面波斜入射下饱和多孔介质成层场地任意时刻的自由场,解决了饱和多孔介质成层场地地震波输入问题. 在典型场地模型下,通过与已有解析解的对比,表明本文方法有效,且具有良好的精度.
附录:
式(16)中单元集中质量矩阵${\pmb M}_{\rm s}^e $, ${\pmb M}_{\rm sf}^e $, ${\pmb M}_{\rm f}^e $, ${\pmb M}_{\rm fs}^e $为,单元阻尼矩阵${\pmb C}_{\rm s}^e $, ${\pmb C}_{\rm sf}^e $, ${\pmb C}_{\rm f}^e $, ${\pmb C}_{\rm fs}^e $,以及单元刚度矩阵${\pmb K}_{\rm s}^e $, ${\pmb K}_{\rm sf}^e $, ${\pmb K}_{\rm f}^e $, ${\pmb K}_{\rm fs}^e $的表达式如下:
${\pmb M}_{\rm s}^e = \dfrac{\Delta z}{2}\left[\!\! \begin{array}{cccc} {\dfrac{A + 2N}{c_x ^2} - \rho _{11} } \!&\! 0 \!&\! 0 \!&\! 0 \\ 0 \!&\! {\dfrac{N}{c_x ^2} - \rho _{11} } \!&\! 0 \!&\! 0 \\ 0 \!&\! 0 \!&\! {\dfrac{A + 2N}{c_x ^2} - \rho _{11} } \!&\! 0 \\ 0 \!&\! 0 \!&\! 0 \!&\! {\dfrac{N}{c_x ^2} - \rho _{11} } \end{array} \!\! \right] (A1)$
${\pmb M}_{\rm sf}^e = {\pmb M}_{\rm fs}^e = \dfrac{\Delta z}{2}\left[\!\! \begin{array}{cccc} {\dfrac{Q}{c_x ^2} - \rho _{12} } & 0 & 0 & 0 \\ 0 & { - \rho _{12} } & 0 & 0 \\ 0 & 0 & {\dfrac{Q}{c_x ^2} - \rho _{12} } & 0 \\ 0 & 0 & 0 & { - \rho _{12} } \end{array} \!\! \right] (A2)$
${\pmb M}_{\rm f}^e = \dfrac{\Delta z}{2}\left[\!\! \begin{array}{cccc} {\dfrac{R}{c_x ^2} - \rho _{22} } & 0 & 0 & 0 \\ 0 & { - \rho _{22} } & 0 & 0 \\ 0 & 0 & {\dfrac{R}{c_x ^2} - \rho _{22} } & 0 \\ 0 & 0 & 0 & { - \rho _{22} } \end{array} \!\! \right] (A3)$
${\pmb C}_{\rm s}^e = \left[\!\! \begin{array}{cccc} { - \dfrac{b\Delta z}{3}} & {\dfrac{A - N}{2c_x }} & { - \dfrac{b\Delta z}{6}} & { - \dfrac{A + N}{2c_x }} \\ { - \dfrac{A - N}{2c_x }} & { - \dfrac{b\Delta z}{3}} & { - \dfrac{A + N}{2c_x }} & { - \dfrac{b\Delta z}{6}} \\ { - \dfrac{b\Delta z}{6}} & {\dfrac{A + N}{2c_x }} & { - \dfrac{b\Delta z}{3}} & { - \dfrac{A - N}{2c_x }} \\ {\dfrac{A + N}{2c_x }} & { - \dfrac{b\Delta z}{6}} & {\dfrac{A - N}{2c_x }} & { - \dfrac{b\Delta z}{3}} \end{array} \!\! \right] (A4)$
${\pmb C}_{\rm sf}^e = {\pmb C}_{\rm fs}^e = \left[\!\! \begin{array}{cccc} {\dfrac{b\Delta z}{3}} & {\dfrac{Q}{2c_x }} & {\dfrac{b\Delta z}{6}} & { - \dfrac{Q}{2c_x }} \\ { - \dfrac{Q}{2c_x }} & {\dfrac{b\Delta z}{3}} & { - \dfrac{Q}{2c_x }} & {\dfrac{b\Delta z}{6}} \\ {\dfrac{b\Delta z}{6}} & {\dfrac{Q}{2c_x }} & {\dfrac{b\Delta z}{3}} & { - \dfrac{Q}{2c_x }} \\ {\dfrac{Q}{2c_x }} & {\dfrac{b\Delta z}{6}} & {\dfrac{Q}{2c_x }} & {\dfrac{b\Delta z}{3}} \end{array} \!\! \right] (A5)$
${\pmb C}_{\rm f}^e = \left[\!\! \begin{array}{cccc} { - \dfrac{b\Delta z}{3}} & {\dfrac{R}{2c_x }} & { - \dfrac{b\Delta z}{6}} & { - \dfrac{R}{2c_x }} \\ { - \dfrac{R}{2c_x }} & { - \dfrac{b\Delta z}{3}} & { - \dfrac{R}{2c_x }} & { - \dfrac{b\Delta z}{6}} \\ { - \dfrac{b\Delta z}{6}} & {\dfrac{R}{2c_x }} & { - \dfrac{b\Delta z}{3}} & { - \dfrac{R}{2c_x }} \\ {\dfrac{R}{2c_x }} & { - \dfrac{b\Delta z}{6}} & {\dfrac{R}{2c_x }} & { - \dfrac{b\Delta z}{3}} \end{array} \!\! \right] (A6)$
${\pmb K}_{\rm s}^e = \dfrac{1}{\Delta z}\left[\!\! \begin{array}{cccc} { - N} & 0 & N & 0 \\ 0 & { - \left( {A + 2N} \right)} & 0 & {A + 2N} \\ N & 0 & { - N} & 0 \\ 0 & {A + 2N} & 0 & { - \left( {A + 2N} \right)} \end{array} \!\! \right] (A7)$
${\pmb K}_{\rm sf}^e ={\pmb K}_{\rm fs}^e = \dfrac{1}{\Delta z}\left[\!\! \begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & { - Q} & 0 & Q \\ 0 & 0 & 0 & 0 \\ 0 & Q & 0 & { - Q} \end{array}\!\! \right] (A8)$
${\pmb K}_{\rm f}^e = \dfrac{1}{\Delta z}\left[\!\! \begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & { - R} & 0 & R \\ 0 & 0 & 0 & 0 \\ 0 & R & 0 & { - R} \end{array} \!\! \right] (A9)$
The authors have declared that no competing interests exist.
参考文献
| [1] |
Statistical research on S-wave incident angle . |
| [2] |
Estimation of earthquake motion incident angle at rock site. Proc of 12th World Conference Earthquake Engineering, NZ National Society for Earthquake Engineering. |
| [3] |
Effects of horizontally traveling waves in soil-structure interaction . |
| [4] |
大型结构地震反应数值模拟中的波动输入 .Wave motion input in numerical simulation of seismic response for large-scale structure . |
| [5] |
地下结构地震响应的计算模型 .A computational model for seismic response analysis of underground stauctures . |
| [6] |
黏弹性人工边界等效载荷计算的改进方法 .An improved method of the calculation of equivalent nodal forces in viscous-elastic artificial boundary . |
| [7] |
Transmission of elastic waves through a stratified solid medium . |
| [8] |
Stiffness matrices for layered soils . |
| [9] |
地震波斜入射时水平层状场地的非线性地震反应 .Nonlinear seismic response of horizontal layered site due to inclined wave . |
| [10] |
地震波斜入射时二维成层介质自由场求解的等效线性化方法 .Two-dimensional equivalent linear seismic analysis of free field in layered half-space due to oblique incidence . |
| [11] |
SH波倾斜入射时土层的非线性响应分析 .Nonlinear responses of layered soils to obliquely incident SH waves . |
| [12] |
地震波斜入射情形下水平成层半空间自由场的时域计算 .The time-step numerical simulation of free field motion of layered half-space for inclined seismic waves . |
| [13] |
成层半空间出平面自由波场的一维化时域算法 .A 1-D time-domain method for 2-D wave motion in elastic layered half-space by antiplane wave oblique incidence . |
| [14] |
成层介质中平面内自由波场的一维化时域算法 .1D time-domain method for in-plane wave motion of free field in layered media . |
| [15] |
A 1D time-domain method for in-plane wave motions in a layered half-space . |
| [16] |
P-SV 波斜入射时成层半空间自由场的时域算法 .Time-domain method for free field in layered half space under P-SV Waves of oblique incidence . |
| [17] |
P-SV 波斜入射时有阻尼成层介质自由波场的一维化时域算法 .A 1D time-domain method for in-plane wave motion of free field in layered media with damping under obliquely incident P-SV waves . |
| [18] |
1D finite element artificial boundary method for layered half space site response from obliquely incident earthquake . |
| [19] |
Theory of propagation of elastic wave in fluid-saturated porous soil . |
| [20] |
Poroelastodynamics: linear models, analytical solutions, and numerical methods . |
| [21] |
饱和两相与单相土互层场地中地铁车站地震反应分析. [博士论文] .Seismic response analysis of subway station in saturated phase and single phase soil. [PhD Thesis] . |
| [22] |
流体饱和两相多孔介质动力反应分析的显式有限元法 .Dynamic analysis of fluid-saturated porous media by using explicit finite element method . |
| [23] |
The elastic coefficients of the theory of consolidation . |
| [24] |
有阻尼振动方程常用显式积分格式稳定性分析 .Stability analysis of an integral method for damped vibration equation . |
| [25] |
有阻尼动力方程显式积分方法的精度研究 .On the accuracy of several explicit integration schemes for dynamic equation with damping . |
| [26] |
两相介质波动问题显式有限元方法稳定性研究 .Study on stability of explicit finite element method for wave motion of fluid-saturated porous media . |
| [27] |
The reflection of plane waves in a poroelastic half-space saturated with inviscid fluid . |
| [28] |
|
| [29] |
非一致地震动场数值方法研究及在结构动力分析中的应用. [博士论文] .Research on the numerical method for asynchronous seismic wave motions and its application in dynamic analysis of atructures. [PhD Thesis] . |
| [30] |
地下水位变化对地震地面运动的影响 .Effects of the groundwater level variation on earthquake ground motions . |

/
| 〈 |
|
〉 |