引 言
颗粒材料是指由大量离散固体颗粒及颗粒间孔隙构成的集合体,其具有强烈的非均匀性与复杂的力学性质,诸如多尺度行为、可 破碎性、各向异性 等 [1 ,2 ,3 ] . 深入研究颗粒材料的基本力学行为不仅有助于减少其生产运输的过程中不必要的浪费,也有助于提高预测和控制诸如泥石流、山 体滑坡等由于颗粒材料变形、破坏而导致的自然灾害[4 ] . 考虑到颗粒材料的离散特性,离散单元法是模拟其力学行为的更加自然与合理的一个方法. 但是在实际应用中,颗粒数量往往十分庞大,其运动规律也很复杂,基于离散单元法模拟和预测工程问题仍然是一个巨大的挑战. 因而,连续体方法或者多尺度方法模拟颗粒材料仍是比较合适与便捷的途径,建立连续体框架下的模型研究其力学行为具有十分重 要的意义[5 ,6 ] .
颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] .
微形态理论[28 ,29 ,30 ,31 ,32 ,33 ] 同样具有描述复杂微结构变形的能力,可以被用于模拟颗粒材料. Misra [28 ] 根据Mindlin[29 ] 和Eringen[30 ] 的微结构线弹性理论建议了基于细观力学方法的颗粒材料微形态模型. 微形态理论假设物体是由宏观物质与细观物质组成的变形协调体,其每个物质点都是一个微结构胞元,并且引入9个变形自由度用以描述微结构的变形与旋转,适用于复杂微结构的变形模拟. 针对颗粒材料Misra等 [28 ] 认为一个物质点即为一个颗粒集合体体积单元,将颗粒运动分解为宏观运动与细观运动两个部分,并基于细观变形能求和得到宏观变形能函数,再通过对宏观变形能求导构建基于细观结构信息表示的宏观本构关系.
近年来,基于颗粒材料冲击与波动响应特性的调控波传播行为的超材料设计引起了研究者的兴趣,为此研究者已开展了大量基于广义连续 体模型(高阶梯度模型或Cosserat连续体模型)的波动分析 [34-36 ] . 正如上文所述,Cosserat连续体模型因包含了可与细观上颗粒转动相关联的转动自由度以及能够反映一定细观结构的内禀特征长度,且相对 简单而受到颗粒材料研究领域的广泛关注[17 ,30 ,34 -35 ,37 ] . 但是Cosserat连续体仅能反映细观结构的刚体转 动 [35 ,38 ] ,考虑到颗粒材料细观结构或者中尺度结构上诸如拉压与剪切等其他变形 模式的重要性[39 ,40 ] , 因而,能够反映细观结构完整运动模式的微形态连续体模型 [29 ,38 ] 引起了研究者的重视[28 ,41 -43 ] . 一阶微形态连续体模型除了描述宏观运动的自由度外,还包含描述微/细观结构变形的自由度,因此在其框架下基于细观途径发展颗粒 材料连续体模型能在一阶梯度情况下为更多细观信息的均匀化提供对应的描述变量.
本文基于Mindlin-Eringen的微结构理论[29 ,30 ] 和Misra的微形态理论 [28 ] ,给出了一个颗粒材料的微形态连续体模型. 不仅对颗粒的平动进行分解,同时对颗粒转动也进行了分解:颗粒运动分解为宏观平均运动(平动与转动)和细观真实运动(平动与转动)两 部分,并认为颗粒的细观真实运动(平动与转动)是由宏观平均运动(平动与转动)与相对运动(平动与转动)组成. 基于此分解,求得相应的细观本构关系和细观变形能函数. 结合宏观变形能的细观变形能求和表达式与细观本构关系的表达式,可获得基于细观量表示的宏观本构关系与相应的本构模量,其中包括了偶应力(相对偶应力)与微曲率(相对微曲率)的关系及其本构模量. 通过推导的微形态模型探讨波在弹性颗粒介质中传播的现象,考察纵波、横波、横向剪切波、横向旋转波的频散关系 [44 ] ,并对其频率带隙[44 ] 进行预测.
1 颗粒的运动描述
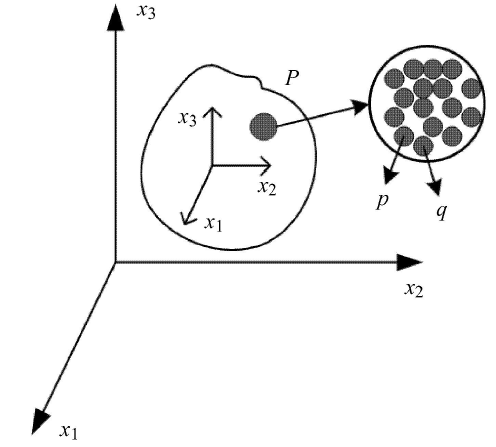
根据Mindlin的微结构理论 [29 ] ,建立一个全局坐标系 x V V P 图1 所示. 然后在 P x ' x ' x 图1 . 考虑 V p q p q [28 ]
ϕ i p = ϕ i q + ϕ i , j q l j + ⋯ (1)
式中, ϕ i l j p q ϕ i x ' x t 29 ]
ψ ij ψ ij = ϕ i , j = ∂ ϕ i ∂ x ' j (2)
此时, ψ ij x t
γ ij γ ij = ψ ij - ϕ ̅ i , j (3)
式中, ϕ ̅ i , j ϕ ̅ i ϕ ̅ i x t ϕ ̅ i = ϕ ̅ i x , t . 那么,宏观应变可以求得为
ε ij = ϕ ̅ ( i , j ) ≡ 1 2 ϕ ̅ i , j + ϕ ̅ j , i (4)
式中, ϕ ̅ ( i , j ) ϕ ̅ i , j
将式(2)代入式(1)中,可以得到颗粒 p q
δ i pq = ϕ i p - ϕ i q + e ijk χ j p r k p - χ j q r k q = ϕ ̅ i , j l j + γ ij l j + e ijk χ j , l l l r k (5)
式中, e ijk χ i r k
δ i M = ϕ ̅ i , j l j , δ i m = γ ij l j , δ i R = e ijk χ j , l l l r k (6)
其中, δ i M δ i m δ i R p q
χ i p = χ i q + χ i , j q l j + ⋯ (7)
那么,这两个颗粒间的相对转动为
θ i pq = χ i , j l j (8)
与位移的分解相似,颗粒的转动可以分解为整个体积元的转动与相对于体积元的转动两个部分,并定义这个相对的转动的梯度
α ij α ij = ( χ i - Γ i ) , j (9)
其中, Γ i
Γ i = e ijk ϕ k , j (10)
那么,式(8)中的相对转动可以表示为
θ i R = θ i pq = χ i , j l j = α ij l j + e ijk φ k , jp l p (11)
对其进行分解,令
θ i s = α ij l j , θ i u = e ijk ϕ k , jp l p (12)
以求得微曲率
κ ij = χ i , j (13)
图1 物质点P V
Fig. 1 Material point P V
2 颗粒的宏细观本构关系
颗粒的宏观变形能密度 W W = W ε ij , γ ij , κ ij , α ij . 从而可以求得与这些变形量共轭的宏观应力量
τ ij = ∂ W ∂ ε ij , σ ij = ∂ W ∂ γ ij , μ ij = ∂ W ∂ κ ij , ν ij = ∂ W ∂ α ij (14)
其中, τ ij σ ij μ ij ν ij [45 ] 认为颗粒材料的宏观变形能密度为颗粒接触间的细观变形能密度 w w w = w δ i M , δ i m , δ i R , θ i R , θ i s , θ i u . 那么,整个体积元的 V
W = 1 V ∑ w δ i M , δ i m , δ i R , θ i R , θ i s , θ i u (15)
对细观变形能密度 w f i m i
∂ w ∂ δ i ξ = f i ξ , ∂ w ∂ θ i η = m i η (16)
其中, ξ = M , m , R η = R , s , u . 式(15)和式(16)代入式(14)中,宏观应力可以用细观尺度上的颗粒接触力来表示
τ ij = ∂ W ∂ ε ij = 1 V ∑ ∂ w ∂ δ k M δ ik l j = 1 V ∑ f i M l j (17)
σ ij = ∂ W ∂ γ ij = 1 V ∑ ∂ w ∂ δ k m δ ik l j = 1 V ∑ f i m l j (18)
μ ij = ∂ W ∂ κ ij = 1 V ∑ ∂ w ∂ δ l R ∂ δ l R ∂ κ ij + ∑ ∂ w ∂ θ l R ∂ θ l R ∂ κ ij = 1 V ∑ f l R e lik l j r k + ∑ m i R l j (19)
ν ij = ∂ W ∂ α ij = 1 V ∑ ∂ w ∂ θ l s ∂ θ l s ∂ α ij = 1 V ∑ m i s l j (20)
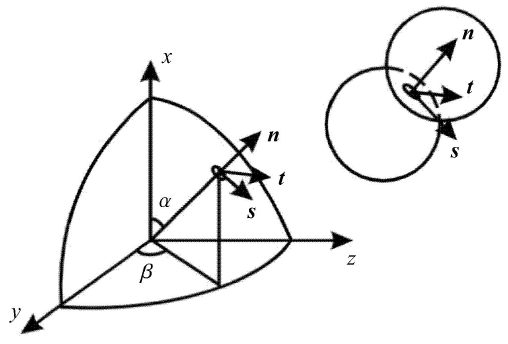
为建立颗粒的细观本构关系,首先对一个颗粒接触对建立局部坐标系,如图2 所示[46 ] . 向量 n s t
n = cos α e 1 + sin α cos β e 2 + sin α sin β e 3 (21)
s = dn d α = - sin α e 1 + cos α cos β e 2 + cos α sin β e 3 (22)
t = n × s = - sin β e 2 + cos β e 3 (23)
其中, e 1 e 2 e 3
忽略法向与切向的交叉项,细观变形能密度 w
w = ∑ ξ f n ξ δ n ξ + f s ξ δ s ξ + f t ξ δ t ξ + m n η θ n η + m s η θ s η + m t η θ t η (24)
图2 颗粒接触的局部坐标[46 ]
Fig. 2 Local coordinate system at a contact of particles[46 ]
其中, ξ = M , m , R η = R , s , u . 下标 n s t
w = 1 2 ∑ ξ K n ξ δ n ξ 2 + K s ξ δ s ξ 2 + K t ξ δ t ξ 2 + G n η θ n η 2 + G s η θ s η 2 + G t η θ t η 2 (25)
其中, K n ξ K s ξ K t ξ G n η G s η G t η s t
K s ξ = K t ξ = K w ξ , G s η = G t η = G w η (26)
通过旋转张量将局部坐标转换为全局坐标,颗粒的细观本构关系可以写为
f i ξ = K ij ξ δ j ξ , K ij ξ = K n ξ n i n j + K w ξ s i s j + t i t j
m i η = G ij η θ j η , G ij η = G n η n i n j + G w η s i s j + t i t j
式中, i , j = 1,2 , 3 . 将式(27)与式(28)代入式(17) ~
τ ij = 1 V ∑ f i M l j = 1 V ∑ K ik M δ k M l j = 1 V ∑ K ik M ε kl l l l j = 1 V ∑ K ik M l l l j ε kl = C ijkl M ε kl (29)
σ ij = 1 V ∑ f i m l j = 1 V ∑ K ik m δ k m l j = 1 V ∑ K ik m γ kl l l l j = 1 V ∑ K ik m l l l j γ kl = C ijkl m γ kl (30)
μ ij = 1 V ∑ f l R e lik l j r k + ∑ m i R l j = 1 V ∑ K lm R δ m R e lik l j r k + ∑ G ik R θ j R l j = 1 V ∑ K nm R e mkq χ k , l l l r q e nip l j r p + ∑ G ik R χ k , l l l l j =
1 V ∑ K nm R e mkq l l r q e nip l j r p + ∑ G ik R l l l j χ k , l = B ijkl R + C ijkl R χ k , l (31)
ν ij = 1 V ∑ m i s l j = 1 V ∑ G ik s θ k s l j = 1 V ∑ G ik s α kl l l l j = 1 V ∑ G ik s l l l j α kl = C ijkl s α kl (32)
3 颗粒的宏观本构参数识别
从式(29) ~ V [47 ] 提出了一个方向分布密度函数 ξ ξ α , β = 1 / 4 π
∫ 0 π ∫ 0 2 π ξ sin α d β d α = 1 (33)
由此能够将式(29) ~
C ijkl M = 1 V ∑ K ik M l l l j = l 2 N V ∫ 0 π ∫ 0 2 π K ik M n l n j ξ sin α d β d α (34)
C ijkl m = 1 V ∑ K ik m l l l j = l 2 N V ∫ 0 π ∫ 0 2 π K ik m n l n j ξ sin α d β d α (35)
B ijkl R = 1 V ∑ K nm R e mkq l l r q e nip l j r p = l 2 r 2 N V ∫ 0 π ∫ 0 2 π K nm R e mkq n l n q e nip n j n p ξ sin α d β d α (36)
C ijkl R = 1 V ∑ G ik R l l l j = l 2 N V ∫ 0 π ∫ 0 2 π G ik R n l n j ξ sin α d β d α (37)
C ijkl s = 1 V ∑ G ik s l l l j = l 2 N V ∫ 0 π ∫ 0 2 π G ik s n l n j ξ sin α d β d α (38)
式中, N V
C iiii ξ = l 2 N V 15 3 K n ξ + 2 K w ξ , C iijj ξ = l 2 N V 15 K n ξ - K w ξ C ijij ξ = l 2 N V 15 K n ξ + 4 K w ξ , C ijji ξ = l 2 N V 15 K n ξ - K w ξ C ijkl ξ = 0 , otherwise (39)
C iiii η = l 2 N V 15 3 G n η + 2 G w η , C iijj η = l 2 N V 15 G n η - G w η C ijij η = l 2 N V 15 G n η + 4 G w η , C ijji η = l 2 N V 15 G n η - G w η C ijkl η = 0 , otherwise (40)
B iiii R = l 2 r 2 N V 15 2 K w R , B iijj R = l 2 r 2 N V 15 - K w R B ijij R = l 2 r 2 N V 15 4 K w R , B ijji R = l 2 r 2 N V 15 - K w R B ijkl R = 0 , otherwise
式中, ξ = M , m , R η = R , s i , j = 1,2 , 3 i ≠ j .
4 平衡方程
根据能量守恒,外力做功转化为动能与势能,则,由哈密顿原理可以得到
δ ∫ 0 t T - W dt + ∫ 0 t δ W ext dt = 0 (42)
其中, W T W ext
上文中假设总势能密度 W W
δ W = τ ij δ ε ij + σ ij δ γ ij + μ ij δ κ ij + ν ij δ α ij =
τ ij δ ϕ ̅ i , j + σ ij δ ϕ i , j - δ ϕ ̅ i , j + μ ij δ χ i , j + ν ij δ χ i , j - e ipq δ ϕ q , pj =
τ ij - σ ij δ ϕ ̅ i , j + σ ij δ ψ ij + ( μ ij + ν ij ) δ χ i , j - ν ij e ipq δ ψ pq , j =
τ ij - σ ij δ ϕ ̅ i , j - τ ij - σ ij , j δ ϕ ̅ i + σ ij δ ψ ij +
μ ij + ν ij δ χ i , j - ( μ ij + ν ij ) , j δ χ i ν ij e ipq δ ψ pq , j + ν kl , l e kij δ ψ ij
那么,可以求得总势能 W
δ W = ∫ V δ WdV = - ∫ V τ ij - σ ij , j δ ϕ ̅ i dV -
∫ V ( μ ij + ν ij ) , j δ χ i dV + ∫ V σ ij + ν kl , l e kij δ ψ ij dV +
∫ S τ ij + σ ij n j δ ϕ ̅ i dS + ∫ S μ ij + ν ij n j δ χ i dS - ∫ S ν ij e ipq n j δ ψ pq dS
同时,根据Mindlin的微结构理论[29 ] ,求得动能的变分为
δ ∫ 0 t Tdt = - ∫ 0 t dt ∫ V ( ρ ϕ ̅ ̈ i δ ϕ ̅ i + 13 ρ ' d 2 ψ ̈ ij δ ψ ij + 23 ρ ' d 2 χ ̈ i δ χ i ) dV
其中, d ρ ρ ' [29 ]
δ W ext = ∫ V f i δ ϕ ̅ i dV + ∫ V m i δ χ i dV + ∫ V Φ ij δ ψ ij dV + ∫ S t i δ ϕ ̅ i dS + ∫ S M i δ χ i dS + ∫ S T ij δ ψ ij dS (46)
其中, f i m i Φ ij t i M i T ij
从而,将式(43) ~
∫ V τ ij - σ ij , j + f i - ρ ϕ ̅ ̈ i δ ϕ ̅ i dV + ∫ V ( μ ij + ν ij ) , j + m i - 23 ρ ' d 2 χ ̈ i δ χ i dV + ∫ V - σ ij - ν kl , l e kij + Φ ij - 13 ρ ' d 2 ψ ̈ ij δ ψ ij dV + ∫ S t i - τ ij - σ ij n j δ ϕ ̅ i dS + ∫ S M i - μ ij + ν ij n j δ χ i dS + ∫ S T i + ν kl e kij n l δ ψ ij dS (47)
为了使式(47)成立,要求式中每一项均为0,那么,就可以得到3组平衡方程的变分
τ ij - σ ij , j + f i = ρ ϕ ̅ ⋅ ⋅ i ( μ ij + ν ij ) , j + m i = 23 ρ ' d 2 χ ̈ i Φ ij - σ ij - ν kl , l e kij = 13 ρ ' d 2 ψ ̈ ij
以及3组边界条件
τ ij - σ ij n j = t i μ ij + ν ij n j = M i T ij + ν kl e kij n l = 0 (49)
5 运动方程与波的传播
将式(29) ~ C ijkl M + C ijkl m ϕ ̅ k , lj - C ijkl m ψ kl , j = ρ ϕ ̅ ⋅ ⋅ i B ijkl R + C ijkl R + C ijkl s χ k , lj - C ijkl s e kmn ψ mn , lj = 2 3 ρ ' d 2 χ ̈ i C ijkl m ϕ ̅ k , l - C ijkl m ψ kl - C klmn s e kij χ m , nl + C klmn s e kij e mpq ψ pq , nl = 13 ρ ' d 2 ψ ̈ ij (50)
其中,忽略 f i m i Φ ij x 1 x 1
ϕ ̅ i = ϕ ̅ i x 1 , t χ i = χ i x 1 , t ψ ij = ψ ij x 1 , t (51)
将式(51)代入式(50)中,得到这15个运动方程具体的分量形式
ρ ϕ ̅ ⋅ ⋅ 1 = C 1111 M + C 1111 m ϕ ̅ 1,11 - C 1111 m ψ 11,1 + C 1122 m ψ 22,1 + C 1133 m ψ 33,1 ρ ϕ ̅ ⋅ ⋅ 2 = C 2121 M + C 2121 m ϕ ̅ 2,11 - C 2112 m ψ 12,1 + C 2121 m ψ 21,1 ρ ϕ ̅ ⋅ ⋅ 3 = C 3131 M + C 3131 m ϕ ̅ 3,11 - C 3113 m ψ 13,1 + C 3131 m ψ 31,1 (52)
2 3 ρ ' d 2 χ ̈ 1 = B 1111 R + C 1111 R + C 1111 s χ 1,11 - C 1111 s ψ 23,11 - ψ 32,11 2 3 ρ ' d 2 χ ̈ 2 = B 2121 R + C 2121 R + C 2121 s χ 2,11 - C 2121 s ψ 31,11 - ψ 13,11 2 3 ρ ' d 2 χ ̈ 3 = B 3131 R + C 3131 R + C 3131 s χ 3,11 - C 3131 s ψ 12,11 - ψ 21,11
1 3 ρ ' d 2 ψ ̈ 11 = C 1111 m ϕ ̅ 1,1 - C 1111 m ψ 11 + C 1122 m ψ 22 + C 1133 m ψ 33 (54 a)
1 3 ρ ' d 2 ψ ̈ 22 = C 2211 m ϕ ̅ 1,1 - C 2211 m ψ 11 + C 2222 m ψ 22 + C 2233 m ψ 33 (54 b)
1 3 ρ ' d 2 ψ ̈ 33 = C 3311 m ϕ ̅ 1,1 - C 3311 m ψ 11 + C 3322 m ψ 22 + C 3333 m ψ 33 (54 c)
1 3 ρ ' d 2 ψ ̈ 12 = C 1221 m ϕ ̅ 2,1 - C 1212 m ψ 12 + C 1221 m ψ 21 - C 3131 s χ 3,11 + C 3131 s ψ 12,11 - ψ 21,11 (54 d)
1 3 ρ ' d 2 ψ ̈ 13 = C 1331 m ϕ ̅ 3,1 - C 1313 m ψ 13 + C 1331 m ψ 31 + C 2121 s χ 2,11 - C 2121 s ψ 31,11 - ψ 13,11 (54 e)
1 3 ρ ' d 2 ψ ̈ 21 = C 2121 m ϕ ̅ 2,1 - C 2112 m ψ 12 + C 2121 m ψ 21 + C 3131 s χ 3,11 - C 3131 s ψ 12,11 - ψ 21,11 (54 f)
1 3 ρ ' d 2 ψ ̈ 23 = - C 2323 m ψ 23 + C 2332 m ψ 32 - C 1111 s χ 1,11 + C 1111 s ψ 23,11 - ψ 32,11 (54 g)
1 3 ρ ' d 2 ψ ̈ 31 = C 3113 m ϕ ̅ 3,1 - C 3113 m ψ 13 + C 3131 m ψ 31 - C 2121 s χ 2,11 + C 2121 s ψ 31,11 - ψ 13,11 (54 h)
1 3 ρ ' d 2 ψ ̈ 32 = - C 3223 m ψ 23 + C 3232 m ψ 32 + C 1111 s χ 1,11 - C 1111 s ψ 23,11 - ψ 32,11 (54 i)
,式(52) ~
ϕ ̅ i = A i i exp i ξ x 1 - ω t χ i = B i exp i ξ x 1 - ω t ψ ij = C ij exp i ξ x 1 - ω t (55)
其中, ξ ω A i B i C ij ~
(A) 式(54b)与式(54c)
1 3 ρ ' d 2 ψ ̈ 22 = C 2211 m ϕ ̅ 1,1 - C 2211 m ψ 11 + C 2222 m ψ 22 + C 2233 m ψ 33 1 3 ρ ' d 2 ψ ̈ 33 = C 3311 m ϕ ̅ 1,1 - C 3311 m ψ 11 + C 3322 m ψ 22 + C 3333 m ψ 33
(B)式(54g)与式(54i)
1 3 ρ ' d 2 ψ ̈ 23 = - C 2323 m ψ 23 + C 2332 m ψ 32 - C 1111 s χ 1,11 + C 1111 s ψ 23,11 - ψ 32,11 1 3 ρ ' d 2 ψ ̈ 32 = - C 3223 m ψ 23 + C 3232 m ψ 32 + C 1111 s χ 1,11 - C 1111 s ψ 23,11 - ψ 32,11
(C) 式(53a), 式(54g)与式(54i)
2 3 ρ ' d 2 χ ̈ 1 = B 1111 R + C 1111 R + C 1111 s χ 1,11 - C 1111 s ψ 23,11 - ψ 32,11
1 3 ρ ' d 2 ψ ̈ 23 = - C 2323 m ψ 23 + C 2332 m ψ 32 - C 1111 s χ 1,11 + C 1111 s ψ 23,11 - ψ 32,11
1 3 ρ ' d 2 ψ ̈ 32 = - C 3223 m ψ 23 + C 3232 m ψ 32 + C 1111 s χ 1,11 - C 1111 s ψ 23,11 - ψ 32,11 ( D) 式(52b), 式(53c), (54d)与(54f)
ρ ϕ ̅ ̈ 2 = C 2121 M + C 2121 m ϕ ̅ 2,11 - C 2112 m ψ 12,1 + C 2121 m ψ 21,1
2 3 ρ ' d 2 χ ̈ 3 = B 3131 R + C 3131 R + C 3131 s χ 3,11 - C 3131 s ψ 12,11 - ψ 21,11
1 3 ρ ' d 2 ψ ̈ 12 = C 1221 m ϕ ̅ 2,1 - C 1212 m ψ 12 + C 1221 m ψ 21 - C 3131 s χ 3,11 + C 3131 s ψ 12,11 - ψ 21,11
1 3 ρ ' d 2 ψ ̈ 21 = C 2121 m ϕ ̅ 2,1 - C 2112 m ψ 12 + C 2121 m ψ 21 + C 3131 s χ 3,11 - C 3131 s ψ 12,11 - ψ 21,11
或者式(52c), (53b), (54e)与式(54h)
ρ ϕ ̅ ̈ 3 = C 3131 M + C 3131 m ϕ ̅ 3,11 - C 3113 m ψ 13,1 + C 3131 m ψ 31,1
2 3 ρ ' d 2 χ ̈ 2 = B 2121 R + C 2121 R + C 2121 s χ 2,11 - C 2121 s ψ 31,11 - ψ 13,11
1 3 ρ ' d 2 ψ ̈ 13 = C 1331 m ϕ ̅ 3,1 - C 1313 m ψ 13 + C 1331 m ψ 31 + C 2121 s χ 2,11 - C 2121 s ψ 31,11 - ψ 13,11
1 3 ρ ' d 2 ψ ̈ 31 = C 3113 m ϕ ̅ 3,1 - C 3113 m ψ 13 + C 3131 m ψ 31 - C 2121 s χ 2,11 + C 2121 s ψ 31,11 - ψ 13,11
(E) 式(52a), 式(54a), 式(54b)与式(54c)
ρ ϕ ̅ ̈ 1 = C 1111 M + C 1111 m ϕ ̅ 1,11 - C 1111 m ψ 11,1 + C 1122 m ψ 22,1 + C 1133 m ψ 33,1
1 3 ρ ' d 2 ψ ̈ 11 = C 1111 m ϕ ̅ 1,1 - C 1111 m ψ 11 + C 1122 m ψ 22 + C 1133 m ψ 33
1 3 ρ ' d 2 ψ ̈ 22 = C 2211 m ϕ ̅ 1,1 - C 2211 m ψ 11 + C 2222 m ψ 22 + C 2233 m ψ 33
1 3 ρ ' d 2 ψ ̈ 33 = C 3311 m ϕ ̅ 1,1 - C 3311 m ψ 11 + C 3322 m ψ 22 + C 3333 m ψ 33
再将式(55)代入这5个方程组,就可以求得关于波数 ξ ω x 1 x 2 x 3 x 2 x 3 χ 1 x 1 x 1 x 2 x 3 x 1 x 1
(A)横向剪切波
1 3 ρ d 2 ω 2 = C 2222 m - C 2233 m (56)
(B)横向剪切波
1 3 ρ d 2 ω 2 = C 2323 m - C 2 332 m (57)
(C)横向旋转波
B 1111 r + C 1111 r + C 1111 s - 2 3 ρ ' d 2 ω 2 ⋅ C 2323 m - C 2332 m - 1 3 ρ ' d 2 ω 2 + 2 C 1111 s ξ 2 = 2 C 1111 s ξ 2 2 (58)
(D)横波
C 3131 M + C 3131 m ξ 2 - ρ ω 2 C 3113 m - C 3131 m 2 ξ C 3113 m + C 3131 m 2 ξ 0 C 1331 m - C 3131 m ξ 2 C 2121 s ξ 2 + C 1313 m - C 1331 m - 13 ρ ' d 2 ω 2 0 2 C 2121 s ξ 2 C 1331 m + C 1313 m ξ 0 C 1331 m + C 1313 m - 13 ρ ' d 2 ω 2 0 0 C 2121 s ξ 2 0 B 2121 R + C 2121 R + C 2121 s ξ 2 - 23 ρ ' d 2 ω 2 = 0 (59)
(E)纵波
C 1111 M + C 1111 m ξ 2 - ρ ω 2 C 1111 m - C 1122 m ξ C 1122 m ξ C 1111 m ξ C 1111 m - C 1122 m - 13 ρ ' d 2 ω 2 C 1122 m C 1111 m + 2 C 1122 m ξ 0 C 1111 m + 2 C 1122 m - 13 ρ ' d 2 ω 2 = 0 (60)
其中,式(58) ~ ξ ω ξ = 0
(A)/(B) 横向剪切波 ω ξ = 0 = ω 2 (61)
(C) 横向旋转波 ω ξ = 0 = ω 3 ω 4 (62)
(D) 横波 ω ξ = 0 = ω 2 ω 3 0 (63)
(E) 纵波 ω ξ = 0 = ω 1 ω 2 0 (64)
其中,将截止频率从大到小排列有 ω 1 > ω 2 > ω 3 > ω 4 > 0
ω 1 = l 2 N V ρ ' d 2 K n m (65 a)
ω 2 = l 2 N V ρ ' d 2 2 K n m + 3 K w m 5 (65 b)
ω 3 = l 2 N V ρ ' d 2 K w m (65 c)
ω 4 = l 2 N V ρ ' d 2 2 r 2 K w R + 3 G n R + 2 G w R + 3 G n s + 2 G w s 10 (65 d)
对于行波来说,可根据截止频率是否为零分为两类:截止频率为零的声波(acoustic wave)与截止频率非零的光波(optical wave). 从式(61) ~
6 结果与讨论
上一部分中推导了横向剪切波、横向旋转波、横波、纵波的频散方程,根据此频散方程,可以求得波数与频率的频散关系. 从频散方 程可以看到,频散关系与细观参数相关. 通常来讲,基于细观尺度的颗粒材料研究一般取法向接触刚度为10 ~ 1 000 MN/m量级,切向接触刚度取为法向接触刚度的0.5倍,滚动刚度取为100 Nm量级. 理论研究中,颗粒的尺度常取为1 mm量级. 本文选取的参数来自Misra等的研究[28 ] ,如表1 所示,那么,上文中非零的截止频率分别为: ω 1 = 8.19 × 1 0 6 ω 2 = 6.86 × 1 0 6 ω 3 = 5.74 × 1 0 6 ω 4 = 77.5
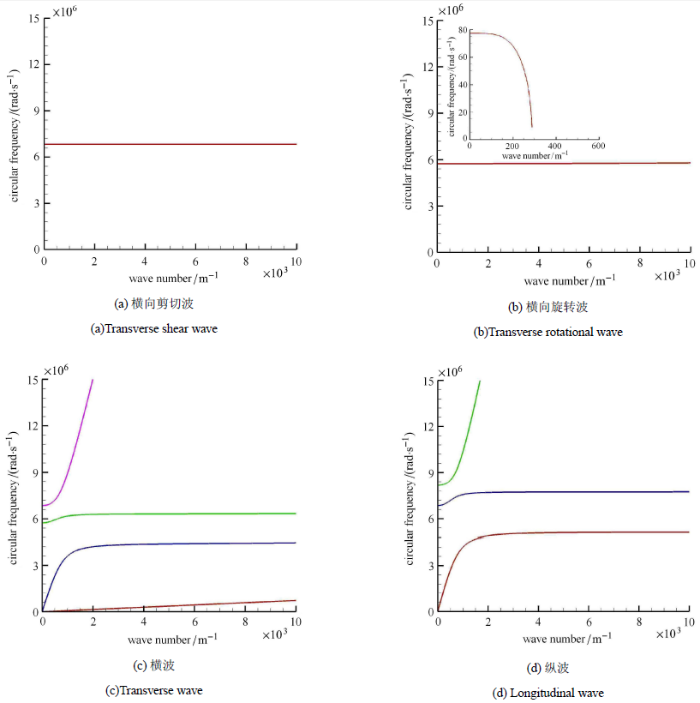
图3 分别给出了表示横向剪切波、横向旋转波、横波与纵波的频散曲线. 从图3 (a)可以看到,对于横向剪切波来讲,只有一条呈平直的光波型的频散曲线,在本文参数取值下, 无论波数为多大,频率始终为 6.86 × 1 0 6 6.86 × 1 0 6 图3 (b)中,横向旋转波也具有一条呈平直的光波型的频散曲线,保持频率为 5.74 × 1 0 6 5.74 × 1 0 6 ~ 77.5 rad/s的横向旋转波能够传递. 从图3 (c)可以看到,横波具有四条频散曲线:第1条为低频线性增长的声波,最后达到 7.26 × 1 0 5 4.46 × 1 0 6 5.74 × 1 0 6 6.34 × 1 0 6 6.86 × 1 0 6 6 ~ 5.74 × 1 0 6 6 ~ 6.86 × 1 0 6 图3 (d),具有3条频散曲线,除不存在低频的曲线外,其变化规律与横波基本相同:第1条频散曲线达到稳定频率 5.13 × 1 0 6 6.86 × 1 0 6 7.75 × 1 0 6 8.19 × 1 0 6 6 ~ 6.86 × 1 0 6 6 ~ 8.19 × 1 0 6 ~ [34 ,48 -49 ] 证实六方密排结构中横向旋转波与频率带隙的 存在.
图3 横向剪切波、横向旋转波、横波与纵波的频散曲线
Fig. 3 Dispersion curves for transverse shear wave, transverse rotational wave, transverse wave and longitudinal wave
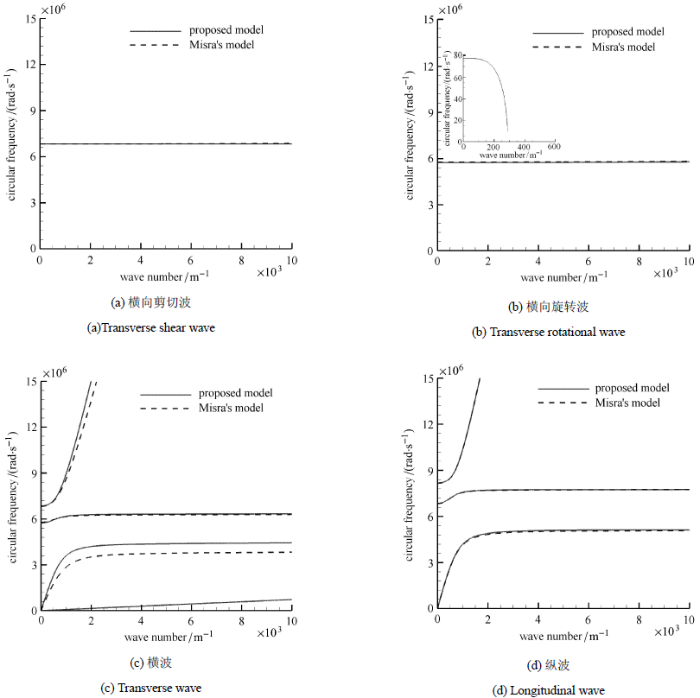
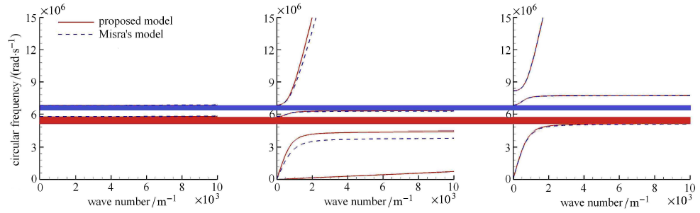
图4 所建议模型与Misra模型[28 ] 的横向剪切波、横向旋转波、横波与纵波的频散曲线对比图
Fig. 4 Dispersion curves of the proposed model vs. Misra model [28 ] for transverse shear wave, transverse rotational wave, transverse wave and longitudinal wave
图4 所示为所建议模型与Misra模型 [28 ] 的横向剪切波、横向旋转波、横波与纵波的频散曲线对比图. 对于横向剪切波,频 散曲线基本重合. 对于横向旋转波,本文所建议模型多具有1条低频的频散曲线,而另1条基本重合. 对于横波,本文所建议模型多具有1条较低频的直线型频散曲线,而另外3条与Misra模型 [28 ] 的频散曲线的变化规律相近,其中1条频散曲线基本重合,所建议模型低频的频率带隙比Misra模型[28 ] 更窄,高频的频率带隙基本一致. 对于纵波,两个模型均具有3条频散曲线,且相互重合,频率带隙基本一致. 横向旋转波与横波同Misra模型所预测存在差异,而其他形式的波基本一致,主要因为本文所建议模型多考虑了一个独立的转动自由度,因而具备了一个考虑转动的变形模式,通过式(52)~式(54)可以反映出来,转动自由度主要影响横向剪切波与横波的频散方程.
图5 所示为所建议模型预测频率带隙的宽度. 从图中可以看到,综合考虑横向剪切波、横向旋转波、横波与纵波的频散曲线,存在两个狭长带(图中红色与蓝色阴影区域),无论波数如何变化,期间均无任何频率的波能够在此介质传播,即此介质的频率带隙为5.13 × 1 0 6 ~ 5.74 × 1 0 6 6 ~ 6.86 × 1 0 6 [28 ] 预测的频率带隙,总体上,频率带隙的宽度相一致,但横波的频率带隙的宽度,本文建议模型所预测要窄于Misra模型,这还是由于所建议模型具有多考虑转动的变形模式的存在所引起的.
图5 所建议模型预测频率带隙
Fig. 5 The frequency band gaps predicted by the proposed model
7 结论
颗粒材料的细观力学方法已经被应用于发展颗粒材料的微形态模型. 基于此方法发展的颗粒材料宏观连续体模型可以反映细观结构信息. 本文针对颗粒材料提出了一个基于细观力学的微形态模型. 首先采用Mindlin-Eringen的微结构理论 [29-30 ] 进行运动分析,对颗粒的平动与转动均进行分解,分解为宏观平均运动(平动与转动)和细观真实运动(平动与转动)两部分,并认为颗粒的细观真实运动(平动与转动)是由宏观平均运动(平动与转动)与相对运动(平动与转动)组成. 基于此分解,求得相应的细观本构关系和细观变形能函数,并且宏观变形能由细观变形能求和得到. 由此可获得基于细观量表示的宏观本构关系与相应的本构模量.
基于所建议的微形态模型预测和探讨波在弹性颗粒介质中传播的现象,考察了纵波、横波、横向剪切波、横向旋转波的频散关系,并对其频率带隙进行预测,主要结论如下:
(1)所建议模型能够模拟频散现象. 由于纵波、横波、横向剪切波、横向旋转波的频散关系分别受宏-细观尺度上的与平动项与转动项相关的参数的影响,其频散曲线各不相同. 横向剪切波具有1条平直的频散曲线;横向旋转波具有1条平直的频散曲线与1条呈双曲线衰减型频散曲线;纵波具有3条频散曲线,且与Misra [28 ] 所预测的频散曲线基本重合;由于所建议模型具有考虑了转动自由度的变形模式,横波具有四条频散曲线,比Misra [28 ] 所预测的多出一条低频的呈线性增长的频散曲线,另外3条变化规律相似且其中一条频散曲线基本重合.
(2)所建议模型预测了弹性颗粒介质的频率带隙. 无论波数如何变化,频率范围为5.13 ×10 6 ~ 5.74 × 1 0 6 6 ~ 6.86 × 1 0 6
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
Li XK Chu XH Feng YT A discrete particle model and numerical modeling of the failure modes of granular materials
.Engineering Computations , 2005 , 22 (8 ): 894 -920
[本文引用: 1]
[2]
Chu XH Yu C Xiu CX et al .Two scale modeling of behaviors of granular structure: Size effects and displacement fluctuations of discrete particle assembly
.Structural Engineering & Mechanics , 2015 , 55 (2 ): 315 -334
[本文引用: 1]
[3]
冯春 , 李世海 , 刘晓宇 . 基于颗粒离散元法的连接键应变软化模型及其应用
. 力学学报 , 2016 , 48 (1 ): 76 -85
[本文引用: 2]
(Feng Chun Li Shihai Liu Xiaoyu Particle-dem based linked bar strain softening model and its application
.Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (1 ): 76 -85 (in Chinese))
[本文引用: 2]
[4]
季顺迎 , 孙珊珊 , 陈晓东 . 颗粒材料剪切流动状态转变的环剪试验研究
. 力学学报 , 2016 , 48 (5 ): 1061 -1072
[本文引用: 1]
(Ji Shunying Sun Shanshan Chen Xiaodong Shear cell test on transition of shear flow states of granular materials
.Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (5 ): 1061 -1072 (in Chinese))
[本文引用: 1]
[5]
白以龙 , 汪海英 , 夏蒙棼 等 . 固体的统计细观力学—连接多个耦合的时空尺度
. 力学进展 , 2006 , 36 (2 ): 286 -305
[本文引用: 1]
(Bai Yilong Wang Haiying Xia Mengfen et al .Statistical mesomechanics of solid, linking coupled multiple space and time scales
.Advances in Mechanics 2006 , 58 (6 ): 286 -305 (in Chinese))
[本文引用: 1]
[6]
Torquato S Haslach H Random heterogeneous materials: Microstructure and macroscopic properties
.Applied Mechanics Reviews , 2002 , 55 (4 ): B62
[本文引用: 1]
[7]
Chang CS Ma L Modeling of discrete granulates as micropolar continua
.Journal of Engineering Mechanics , 1990 , 116 (12 ): 2703 -2721
[本文引用: 2]
[8]
Eringen AC Suhubi ES Nonlinear theory of simple micro-elastic solids—I
.International Journal of Engineering Science , 1964 , 2 (2 ): 189 -203
[本文引用: 2]
[9]
Eringen AC Suhubi ES Nonlinear theory of simple micro-elastic solids—II
.International Journal of Engineering Science , 1964 , 2 (4 ): 389 -404
[本文引用: 1]
[10]
Stojanovi R On the mechanics of materials with microstructure
.Acta Mechanica , 1972 , 15 (3-4 ): 261 -273
[本文引用: 1]
[11]
Mühlhaus HB Application of Cosserat theory in numerical solutions of limit load problems
.Archive of Applied Mechanics , 1989 , 59 (2 ): 124 -137
[本文引用: 1]
[12]
Li XK Tang HX A consistent return mapping algorithm for pressure-dependent elastoplastic Cosserat continua and modelling of strain localisation
.Computers & Structures , 2005 , 83 (1 ): 1 -10
[本文引用: 1]
[13]
Granik VT Ferrari M Microstructural mechanics of granular media
.Mechanics of Materials , 1993 , 15 (4 ): 301 -322
[本文引用: 2]
[14]
Christoffersen J Mehrabadi MM Nematnasser S A micromechanical description of granular material behavior
.Journal of Applied Mechanics , 1981 , 48 (2 ): 339
[本文引用: 3]
[15]
Mehrabadi MM Nemat-Nasser S Stress, dilatancy and fabric in granular materials
.Mechanics of Materials , 1983 , 2 (2 ): 155 -161
[本文引用: 2]
[16]
唐洪祥 , 李锡夔 . Cosserat连续体模型中本构参数对应变局部化模拟结果影响的数值分析
. 计算力学学报 , 2008 , 25 (5 ): 676 -681
[本文引用: 1]
(Tang Hongxiang Li Xikui Numerical analysis for the effects of constitutive parameters in Cosserat continuum model on the simulation results of the strain localization
.Chinese Journal of Computational Mechanics 2008 , 25 (5 ): 676 -681 (in Chinese))
[本文引用: 1]
[17]
Li XK Liu QP Zhang JB A micro-macro homogenization approach for discrete particle assembly-Cosserat continuum modeling of granular materials
.International Journal of Solids and Structures, 2010 , 47 (2 ): 291 -303
[本文引用: 1]
[18]
Chang JF Chu XH Xu YJ Finite-element analysis of failure in transversely isotropic geomaterials
. International Journal of Geomechanics , 2014 , 15 (6 ): 04014096
[本文引用: 1]
[19]
Gennes PG Granular matter: A tentative view
.Reviews of Modern Physics , 1999 , 71 (2 ): S374
[本文引用: 2]
[20]
Chang CS Chang Y Kabir MG Micromechanics modeling for stress-strain behavior of granular soils I: Theory
.Journal of Geotechnical Engineering , 1992 , 118 (12 ): 1959 -1974
[本文引用: 2]
[21]
Chang CS Kuhn MR On virtual work and stress in granular media
.International Journal of Solids & Structures , 2005 , 42 (13 ): 3773 -3793
[本文引用: 1]
[22]
Saxcé GD Fortin J Millet O About the numerical simulation of the dynamics of granular media and the definition of the mean stress tensor
.Mechanics of Materials , 2004 , 36 (12 ): 1175 -1184
[本文引用: 1]
[23]
Kruyt NP Statics and kinematics of discrete Cosserat-type granular materials
.International Journal of Solids & Structures , 2003 , 40 (3 ): 511 -534
[本文引用: 1]
[24]
Bonelli S Millet O Nicot F et al .On the definition of an average strain tensor for two-dimensional granular material assemblies
.International Journal of Solids & Structures , 2012 , 49 (7-8 ): 947 -958
[本文引用: 1]
[25]
Kruyt NP Millet O Nicot F Macroscopic strains in granular materials accounting for grain rotations
.Granular Matter , 2014 , 16 (6 ): 933 -944
[本文引用: 1]
[26]
Chang CS Liao CL Constitutive relation for a particulate medium with the effect of particle rotation
.International Journal of Solids & Structures , 1990 , 26 (4 ): 437 -453
[本文引用: 1]
[27]
Chang CS Gao J Second-gradient constitutive theory for granular material with random packing structure
.International Journal of Solids & Structures , 1995 , 32 (16 ): 2279 -2293
[本文引用: 1]
[28]
Misra A Poorsolhjouy P Granular micromechanics based micromorphic model predicts frequency band gaps
.Continuum Mechanics & Thermodynamics , 2016 , 28 (1-2 ): 215 -234
[本文引用: 15]
[29]
Mindlin RD Micro-structure in linear elasticity
.Archive for Rational Mechanics and Analysis , 1964 , 16 (1 ): 51 -78
[本文引用: 8]
[30]
Eringen AC Microcontinuum Field Theories: Foundations and Solids
. New York: Springer , 1999
[本文引用: 4]
[31]
Neff P Ghiba ID Madeo A et al .A unifying perspective: the relaxed linear micromorphic continuum
.Continuum Mechanics & Thermodynamics , 2014 , 26 (5 ): 639 -681
[本文引用: 1]
[32]
Ghiba ID Neff P Madeo A et al .The relaxed linear micromorphic continuum: Existence, uniqueness and continuous dependence in dynamics
.Mathematics & Mechanics of Solids , 2015 , 20 (10 ): 1171 -1197
[本文引用: 1]
[33]
Neff P Ghiba ID Lazar M et al .The relaxed linear micromorphic continuum: Well-posedness of the static problem and relations to the gauge theory of dislocations
.The Quarterly Journal of Mechanics and Applied Mathematics , 2015 , 68 (1 ): 53 -84
[本文引用: 1]
[34]
Merkel A Luding S Enhanced micropolar model for wave propagation in ordered granular materials
.International Journal of Solids & Structures , 2017 , 106 : 91 -105
[本文引用: 2]
[35]
Maugin GA Metrikine AV Mechanics of Generalized Continua: One Hundred Years After the Cosserats. Berlin, Heidelerg:
Springer-Verlag , 2010
[本文引用: 2]
[36]
Askes H Aifantis EC Gradient elasticity in statics and dynamics: An overview of formulations, length scale identification procedures, finite element implementations and new results
.International Journal of Solids & Structures , 2011 , 48 : 1962 -1990
[37]
Muhlhaus HB Oka F Dispersion and wave propagation in discrete and continuous models for granular materials
.International Journal of Solids & Structures , 1996 , 33 : 2841 -2858
[本文引用: 1]
[38]
Huang WX Sloan SW Sheng DC Analysis of plane Couette shear test of granular media in a Cosserat continuum approach
.Mechanics of Materials , 2014 , 69 : 106 -115
[本文引用: 2]
[39]
Tordesillas A Muthuswamy M Walsh SDC Mesoscale measures of nonaffine deformation in dense granular assemblies
.Journal of Engineering Mechanics , 2008 , 134 : 1095 -1113
[本文引用: 1]
[40]
Jiang MJ Yu HS Harris D Kinematic variables bridging discrete and continuum granular mechanics
.Mechanics Research Communications , 2006 , 33 : 651 -666
[本文引用: 1]
[41]
Lee JD Wang XQ Generalized micromorphic solids and fluids
.International Journal of Solids & Structures , 2011 , 49 : 1378 -1387
[本文引用: 1]
[42]
Hutter G Homogenization of a Cauchy continuum towards a micromorphic continuum
.Journal of the Mechanics and Physics , 2017 , 99 : 394 -408
[43]
Forest S Nonlinear regularization operators as a derived from the micromorphic approach to gradient elasticity, viscoplasticity and damage
.Proceedings of the Royal Society A , 2016 , 472 : 20150755
[本文引用: 1]
[44]
马天雪 , 苏晓星 , 董浩文 等 . 声光子晶体带隙特性与声光耦合作用研究综述
. 力学学报 , 2017 , 49 (4 ): 743 -757
[本文引用: 2]
(Ma Tianxue Su Xiaoxing Dong Haowen et al .Review of bandgap characteristics and acousto-optical coupling in phoxonic crystals
.Chinese Journal of Theoretical and Applied Mechanics 2017 , 49 (4 ): 743 -757 (in Chinese))
[本文引用: 2]
[45]
Tordesillas A Walsh DCS Incorporating rolling resistance and contact anisotropy in micromechanical models of granular media
.Powder Technology , 2002 , 124 (1-2 ): 106 -111
[本文引用: 1]
[46]
Hicher PY Chang CS Elastic model for partially saturated granular materials
.Journal of Engineering Mechanics , 2008 , 134 (6 ): 505 -513
[本文引用: 3]
[47]
Chang CS Lun M Elastic material constants for isotropic granular solids with particle rotation
.International Journal of Solids & Structures , 1992 , 29 (8 ): 1001 -10
[本文引用: 1]
[48]
Merkel A Tournat V Gusev V Dispersion of elastic waves in three-dimensional noncohesive granular phononic crystals: properties of rotational modes
.Physical Review E , 2010 , 82 (3 Pt 1 ): 031305
[本文引用: 1]
[49]
Merkel A Tournat V Gusev V Experimental evidence of rotational elastic waves in granular phononic crystals
.Physical Review Letters , 2011 , 107 (22 ): 225502
[本文引用: 1]
A discrete particle model and numerical modeling of the failure modes of granular materials
1
2005
... 颗粒材料是指由大量离散固体颗粒及颗粒间孔隙构成的集合体,其具有强烈的非均匀性与复杂的力学性质,诸如多尺度行为、可 破碎性、各向异性 等 [1 ,2 ,3 ] . 深入研究颗粒材料的基本力学行为不仅有助于减少其生产运输的过程中不必要的浪费,也有助于提高预测和控制诸如泥石流、山 体滑坡等由于颗粒材料变形、破坏而导致的自然灾害[4 ] . 考虑到颗粒材料的离散特性,离散单元法是模拟其力学行为的更加自然与合理的一个方法. 但是在实际应用中,颗粒数量往往十分庞大,其运动规律也很复杂,基于离散单元法模拟和预测工程问题仍然是一个巨大的挑战. 因而,连续体方法或者多尺度方法模拟颗粒材料仍是比较合适与便捷的途径,建立连续体框架下的模型研究其力学行为具有十分重 要的意义[5 ,6 ] . ...
Two scale modeling of behaviors of granular structure: Size effects and displacement fluctuations of discrete particle assembly
1
2015
... 颗粒材料是指由大量离散固体颗粒及颗粒间孔隙构成的集合体,其具有强烈的非均匀性与复杂的力学性质,诸如多尺度行为、可 破碎性、各向异性 等 [1 ,2 ,3 ] . 深入研究颗粒材料的基本力学行为不仅有助于减少其生产运输的过程中不必要的浪费,也有助于提高预测和控制诸如泥石流、山 体滑坡等由于颗粒材料变形、破坏而导致的自然灾害[4 ] . 考虑到颗粒材料的离散特性,离散单元法是模拟其力学行为的更加自然与合理的一个方法. 但是在实际应用中,颗粒数量往往十分庞大,其运动规律也很复杂,基于离散单元法模拟和预测工程问题仍然是一个巨大的挑战. 因而,连续体方法或者多尺度方法模拟颗粒材料仍是比较合适与便捷的途径,建立连续体框架下的模型研究其力学行为具有十分重 要的意义[5 ,6 ] . ...
基于颗粒离散元法的连接键应变软化模型及其应用
2
2016
... 颗粒材料是指由大量离散固体颗粒及颗粒间孔隙构成的集合体,其具有强烈的非均匀性与复杂的力学性质,诸如多尺度行为、可 破碎性、各向异性 等 [1 ,2 ,3 ] . 深入研究颗粒材料的基本力学行为不仅有助于减少其生产运输的过程中不必要的浪费,也有助于提高预测和控制诸如泥石流、山 体滑坡等由于颗粒材料变形、破坏而导致的自然灾害[4 ] . 考虑到颗粒材料的离散特性,离散单元法是模拟其力学行为的更加自然与合理的一个方法. 但是在实际应用中,颗粒数量往往十分庞大,其运动规律也很复杂,基于离散单元法模拟和预测工程问题仍然是一个巨大的挑战. 因而,连续体方法或者多尺度方法模拟颗粒材料仍是比较合适与便捷的途径,建立连续体框架下的模型研究其力学行为具有十分重 要的意义[5 ,6 ] . ...
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
基于颗粒离散元法的连接键应变软化模型及其应用
2
2016
... 颗粒材料是指由大量离散固体颗粒及颗粒间孔隙构成的集合体,其具有强烈的非均匀性与复杂的力学性质,诸如多尺度行为、可 破碎性、各向异性 等 [1 ,2 ,3 ] . 深入研究颗粒材料的基本力学行为不仅有助于减少其生产运输的过程中不必要的浪费,也有助于提高预测和控制诸如泥石流、山 体滑坡等由于颗粒材料变形、破坏而导致的自然灾害[4 ] . 考虑到颗粒材料的离散特性,离散单元法是模拟其力学行为的更加自然与合理的一个方法. 但是在实际应用中,颗粒数量往往十分庞大,其运动规律也很复杂,基于离散单元法模拟和预测工程问题仍然是一个巨大的挑战. 因而,连续体方法或者多尺度方法模拟颗粒材料仍是比较合适与便捷的途径,建立连续体框架下的模型研究其力学行为具有十分重 要的意义[5 ,6 ] . ...
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
颗粒材料剪切流动状态转变的环剪试验研究
1
2016
... 颗粒材料是指由大量离散固体颗粒及颗粒间孔隙构成的集合体,其具有强烈的非均匀性与复杂的力学性质,诸如多尺度行为、可 破碎性、各向异性 等 [1 ,2 ,3 ] . 深入研究颗粒材料的基本力学行为不仅有助于减少其生产运输的过程中不必要的浪费,也有助于提高预测和控制诸如泥石流、山 体滑坡等由于颗粒材料变形、破坏而导致的自然灾害[4 ] . 考虑到颗粒材料的离散特性,离散单元法是模拟其力学行为的更加自然与合理的一个方法. 但是在实际应用中,颗粒数量往往十分庞大,其运动规律也很复杂,基于离散单元法模拟和预测工程问题仍然是一个巨大的挑战. 因而,连续体方法或者多尺度方法模拟颗粒材料仍是比较合适与便捷的途径,建立连续体框架下的模型研究其力学行为具有十分重 要的意义[5 ,6 ] . ...
颗粒材料剪切流动状态转变的环剪试验研究
1
2016
... 颗粒材料是指由大量离散固体颗粒及颗粒间孔隙构成的集合体,其具有强烈的非均匀性与复杂的力学性质,诸如多尺度行为、可 破碎性、各向异性 等 [1 ,2 ,3 ] . 深入研究颗粒材料的基本力学行为不仅有助于减少其生产运输的过程中不必要的浪费,也有助于提高预测和控制诸如泥石流、山 体滑坡等由于颗粒材料变形、破坏而导致的自然灾害[4 ] . 考虑到颗粒材料的离散特性,离散单元法是模拟其力学行为的更加自然与合理的一个方法. 但是在实际应用中,颗粒数量往往十分庞大,其运动规律也很复杂,基于离散单元法模拟和预测工程问题仍然是一个巨大的挑战. 因而,连续体方法或者多尺度方法模拟颗粒材料仍是比较合适与便捷的途径,建立连续体框架下的模型研究其力学行为具有十分重 要的意义[5 ,6 ] . ...
固体的统计细观力学—连接多个耦合的时空尺度
1
2006
... 颗粒材料是指由大量离散固体颗粒及颗粒间孔隙构成的集合体,其具有强烈的非均匀性与复杂的力学性质,诸如多尺度行为、可 破碎性、各向异性 等 [1 ,2 ,3 ] . 深入研究颗粒材料的基本力学行为不仅有助于减少其生产运输的过程中不必要的浪费,也有助于提高预测和控制诸如泥石流、山 体滑坡等由于颗粒材料变形、破坏而导致的自然灾害[4 ] . 考虑到颗粒材料的离散特性,离散单元法是模拟其力学行为的更加自然与合理的一个方法. 但是在实际应用中,颗粒数量往往十分庞大,其运动规律也很复杂,基于离散单元法模拟和预测工程问题仍然是一个巨大的挑战. 因而,连续体方法或者多尺度方法模拟颗粒材料仍是比较合适与便捷的途径,建立连续体框架下的模型研究其力学行为具有十分重 要的意义[5 ,6 ] . ...
固体的统计细观力学—连接多个耦合的时空尺度
1
2006
... 颗粒材料是指由大量离散固体颗粒及颗粒间孔隙构成的集合体,其具有强烈的非均匀性与复杂的力学性质,诸如多尺度行为、可 破碎性、各向异性 等 [1 ,2 ,3 ] . 深入研究颗粒材料的基本力学行为不仅有助于减少其生产运输的过程中不必要的浪费,也有助于提高预测和控制诸如泥石流、山 体滑坡等由于颗粒材料变形、破坏而导致的自然灾害[4 ] . 考虑到颗粒材料的离散特性,离散单元法是模拟其力学行为的更加自然与合理的一个方法. 但是在实际应用中,颗粒数量往往十分庞大,其运动规律也很复杂,基于离散单元法模拟和预测工程问题仍然是一个巨大的挑战. 因而,连续体方法或者多尺度方法模拟颗粒材料仍是比较合适与便捷的途径,建立连续体框架下的模型研究其力学行为具有十分重 要的意义[5 ,6 ] . ...
Random heterogeneous materials: Microstructure and macroscopic properties
1
2002
... 颗粒材料是指由大量离散固体颗粒及颗粒间孔隙构成的集合体,其具有强烈的非均匀性与复杂的力学性质,诸如多尺度行为、可 破碎性、各向异性 等 [1 ,2 ,3 ] . 深入研究颗粒材料的基本力学行为不仅有助于减少其生产运输的过程中不必要的浪费,也有助于提高预测和控制诸如泥石流、山 体滑坡等由于颗粒材料变形、破坏而导致的自然灾害[4 ] . 考虑到颗粒材料的离散特性,离散单元法是模拟其力学行为的更加自然与合理的一个方法. 但是在实际应用中,颗粒数量往往十分庞大,其运动规律也很复杂,基于离散单元法模拟和预测工程问题仍然是一个巨大的挑战. 因而,连续体方法或者多尺度方法模拟颗粒材料仍是比较合适与便捷的途径,建立连续体框架下的模型研究其力学行为具有十分重 要的意义[5 ,6 ] . ...
Modeling of discrete granulates as micropolar continua
2
1990
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
... [7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ]. 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
Nonlinear theory of simple micro-elastic solids—I
2
1964
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
... [8 -13 ,16 -18 ]十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
Nonlinear theory of simple micro-elastic solids—II
1
1964
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
On the mechanics of materials with microstructure
1
1972
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
Application of Cosserat theory in numerical solutions of limit load problems
1
1989
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
A consistent return mapping algorithm for pressure-dependent elastoplastic Cosserat continua and modelling of strain localisation
1
2005
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
Microstructural mechanics of granular media
2
1993
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
... -13 ,16 -18 ]十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
A micromechanical description of granular material behavior
3
1981
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
... [14 ]. Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
... [14 ,15 ]为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
Stress, dilatancy and fabric in granular materials
2
1983
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
... ,15 ]为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
Cosserat连续体模型中本构参数对应变局部化模拟结果影响的数值分析
1
2008
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
Cosserat连续体模型中本构参数对应变局部化模拟结果影响的数值分析
1
2008
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
A micro-macro homogenization approach for discrete particle assembly-Cosserat continuum modeling of granular materials
1
2010
... 近年来,基于颗粒材料冲击与波动响应特性的调控波传播行为的超材料设计引起了研究者的兴趣,为此研究者已开展了大量基于广义连续 体模型(高阶梯度模型或Cosserat连续体模型)的波动分析 [34-36 ] . 正如上文所述,Cosserat连续体模型因包含了可与细观上颗粒转动相关联的转动自由度以及能够反映一定细观结构的内禀特征长度,且相对 简单而受到颗粒材料研究领域的广泛关注[17 ,30 ,34 -35 ,37 ] . 但是Cosserat连续体仅能反映细观结构的刚体转 动 [35 ,38 ] ,考虑到颗粒材料细观结构或者中尺度结构上诸如拉压与剪切等其他变形 模式的重要性[39 ,40 ] , 因而,能够反映细观结构完整运动模式的微形态连续体模型 [29 ,38 ] 引起了研究者的重视[28 ,41 -43 ] . 一阶微形态连续体模型除了描述宏观运动的自由度外,还包含描述微/细观结构变形的自由度,因此在其框架下基于细观途径发展颗粒 材料连续体模型能在一阶梯度情况下为更多细观信息的均匀化提供对应的描述变量. ...
Finite-element analysis of failure in transversely isotropic geomaterials
1
2014
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
Granular matter: A tentative view
2
1999
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
... [19 ,20 ,21 ,22 ,23 ,24 ,25 ]致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
Micromechanics modeling for stress-strain behavior of granular soils I: Theory
2
1992
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
... [20 ]将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
On virtual work and stress in granular media
1
2005
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
About the numerical simulation of the dynamics of granular media and the definition of the mean stress tensor
1
2004
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
Statics and kinematics of discrete Cosserat-type granular materials
1
2003
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
On the definition of an average strain tensor for two-dimensional granular material assemblies
1
2012
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
Macroscopic strains in granular materials accounting for grain rotations
1
2014
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
Constitutive relation for a particulate medium with the effect of particle rotation
1
1990
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
Second-gradient constitutive theory for granular material with random packing structure
1
1995
... 颗粒材料的宏观性质与细观尺度上的颗粒排布、接触刚度等信息密切相关 [3 ] . Chang等 [7 ] 认为通过微结构连续体途径(microstructural continuum approach)可以考虑细观结构的影响,基于能够反映细观离散特性的宏观变形量,得到宏观尺度上的本构关系. 这种方法已被 大量用于研究颗粒材料的力学行为中[7 ,8 ,9 ,10 ,11 ,12 ,13 ,14 ,15 ] . 其中,Cosserat理论[8 -13 ,16 -18 ] 十分具有代表性且得到了广泛应用. 该理论通过引入旋转自由度,推导出与其对应的偶应力及表征细观结构信息的特征长度,从而适合模拟颗粒材料的微结构, 且更加符合颗粒材料的物理实际. 但是,经典Cosserat理论只能部分表征微结构信息,不能与颗粒材料的离散结构特性建立显式联系[14 ] . Nemat-Nasser等 [14 ,15 ] 为表征微结构特性,引入了结构张量,并建立起其与宏观应力的联系,使本构关系能 够反映微结构的演化,从而发展出基于细观力学的连续介质描述. 该理论通过应力、应变概念描述颗粒材料的宏观变形行为,基于相互接触的颗粒间的局部运动及力学行为建立细观本构关系, 其关键是如何建立颗粒材料离散的细观力学响应与宏观上连续行为之间的联 系[19 ] . 考虑颗粒材料的细观离散特性,基于经典连续体的应力应变定义不再适用,大量研究[19 ,20 ,21 ,22 ,23 ,24 ,25 ] 致力于发展颗粒材料细观结构的描述、细观结构应力应变的定义以及采用均一化方法建立宏细观的联系. 如Chang等[20 ] 将颗粒材料的本构关系划分为3个层次:表征元、微单元及颗粒接触,以表征元体现宏观应力应变关系,以微单元体现局部应力应变关系,以颗粒接触体现力与位移的关系. 并基于Vogit均一化理论应用最优拟合假设、运动假设、静态假设等建立颗粒材料宏细观联系及本构关系[26 ,27 ] . ...
Granular micromechanics based micromorphic model predicts frequency band gaps
15
2016
... 微形态理论[28 ,29 ,30 ,31 ,32 ,33 ] 同样具有描述复杂微结构变形的能力,可以被用于模拟颗粒材料. Misra [28 ] 根据Mindlin[29 ] 和Eringen[30 ] 的微结构线弹性理论建议了基于细观力学方法的颗粒材料微形态模型. 微形态理论假设物体是由宏观物质与细观物质组成的变形协调体,其每个物质点都是一个微结构胞元,并且引入9个变形自由度用以描述微结构的变形与旋转,适用于复杂微结构的变形模拟. 针对颗粒材料Misra等 [28 ] 认为一个物质点即为一个颗粒集合体体积单元,将颗粒运动分解为宏观运动与细观运动两个部分,并基于细观变形能求和得到宏观变形能函数,再通过对宏观变形能求导构建基于细观结构信息表示的宏观本构关系. ...
... [28 ]根据Mindlin[29 ] 和Eringen[30 ] 的微结构线弹性理论建议了基于细观力学方法的颗粒材料微形态模型. 微形态理论假设物体是由宏观物质与细观物质组成的变形协调体,其每个物质点都是一个微结构胞元,并且引入9个变形自由度用以描述微结构的变形与旋转,适用于复杂微结构的变形模拟. 针对颗粒材料Misra等 [28 ] 认为一个物质点即为一个颗粒集合体体积单元,将颗粒运动分解为宏观运动与细观运动两个部分,并基于细观变形能求和得到宏观变形能函数,再通过对宏观变形能求导构建基于细观结构信息表示的宏观本构关系. ...
... [28 ]认为一个物质点即为一个颗粒集合体体积单元,将颗粒运动分解为宏观运动与细观运动两个部分,并基于细观变形能求和得到宏观变形能函数,再通过对宏观变形能求导构建基于细观结构信息表示的宏观本构关系. ...
... 近年来,基于颗粒材料冲击与波动响应特性的调控波传播行为的超材料设计引起了研究者的兴趣,为此研究者已开展了大量基于广义连续 体模型(高阶梯度模型或Cosserat连续体模型)的波动分析 [34-36 ] . 正如上文所述,Cosserat连续体模型因包含了可与细观上颗粒转动相关联的转动自由度以及能够反映一定细观结构的内禀特征长度,且相对 简单而受到颗粒材料研究领域的广泛关注[17 ,30 ,34 -35 ,37 ] . 但是Cosserat连续体仅能反映细观结构的刚体转 动 [35 ,38 ] ,考虑到颗粒材料细观结构或者中尺度结构上诸如拉压与剪切等其他变形 模式的重要性[39 ,40 ] , 因而,能够反映细观结构完整运动模式的微形态连续体模型 [29 ,38 ] 引起了研究者的重视[28 ,41 -43 ] . 一阶微形态连续体模型除了描述宏观运动的自由度外,还包含描述微/细观结构变形的自由度,因此在其框架下基于细观途径发展颗粒 材料连续体模型能在一阶梯度情况下为更多细观信息的均匀化提供对应的描述变量. ...
... 本文基于Mindlin-Eringen的微结构理论[29 ,30 ] 和Misra的微形态理论 [28 ] ,给出了一个颗粒材料的微形态连续体模型. 不仅对颗粒的平动进行分解,同时对颗粒转动也进行了分解:颗粒运动分解为宏观平均运动(平动与转动)和细观真实运动(平动与转动)两 部分,并认为颗粒的细观真实运动(平动与转动)是由宏观平均运动(平动与转动)与相对运动(平动与转动)组成. 基于此分解,求得相应的细观本构关系和细观变形能函数. 结合宏观变形能的细观变形能求和表达式与细观本构关系的表达式,可获得基于细观量表示的宏观本构关系与相应的本构模量,其中包括了偶应力(相对偶应力)与微曲率(相对微曲率)的关系及其本构模量. 通过推导的微形态模型探讨波在弹性颗粒介质中传播的现象,考察纵波、横波、横向剪切波、横向旋转波的频散关系 [44 ] ,并对其频率带隙[44 ] 进行预测. ...
... 根据Mindlin的微结构理论 [29 ] ,建立一个全局坐标系 x V V P 图1 所示. 然后在 P x ' x ' x 图1 . 考虑 V p q p q [28 ] ...
... 上一部分中推导了横向剪切波、横向旋转波、横波、纵波的频散方程,根据此频散方程,可以求得波数与频率的频散关系. 从频散方 程可以看到,频散关系与细观参数相关. 通常来讲,基于细观尺度的颗粒材料研究一般取法向接触刚度为10 ~ 1 000 MN/m量级,切向接触刚度取为法向接触刚度的0.5倍,滚动刚度取为100 Nm量级. 理论研究中,颗粒的尺度常取为1 mm量级. 本文选取的参数来自Misra等的研究[28 ] ,如表1 所示,那么,上文中非零的截止频率分别为: ω 1 = 8.19 × 1 0 6 ω 2 = 6.86 × 1 0 6 ω 3 = 5.74 × 1 0 6 ω 4 = 77.5
... 所建议模型与Misra模型[28 ] 的横向剪切波、横向旋转波、横波与纵波的频散曲线对比图 ...
... Dispersion curves of the proposed model vs. Misra model [28 ] for transverse shear wave, transverse rotational wave, transverse wave and longitudinal wave ...
... 图4 所示为所建议模型与Misra模型 [28 ] 的横向剪切波、横向旋转波、横波与纵波的频散曲线对比图. 对于横向剪切波,频 散曲线基本重合. 对于横向旋转波,本文所建议模型多具有1条低频的频散曲线,而另1条基本重合. 对于横波,本文所建议模型多具有1条较低频的直线型频散曲线,而另外3条与Misra模型 [28 ] 的频散曲线的变化规律相近,其中1条频散曲线基本重合,所建议模型低频的频率带隙比Misra模型[28 ] 更窄,高频的频率带隙基本一致. 对于纵波,两个模型均具有3条频散曲线,且相互重合,频率带隙基本一致. 横向旋转波与横波同Misra模型所预测存在差异,而其他形式的波基本一致,主要因为本文所建议模型多考虑了一个独立的转动自由度,因而具备了一个考虑转动的变形模式,通过式(52)~式(54)可以反映出来,转动自由度主要影响横向剪切波与横波的频散方程. ...
... [28 ]的频散曲线的变化规律相近,其中1条频散曲线基本重合,所建议模型低频的频率带隙比Misra模型[28 ] 更窄,高频的频率带隙基本一致. 对于纵波,两个模型均具有3条频散曲线,且相互重合,频率带隙基本一致. 横向旋转波与横波同Misra模型所预测存在差异,而其他形式的波基本一致,主要因为本文所建议模型多考虑了一个独立的转动自由度,因而具备了一个考虑转动的变形模式,通过式(52)~式(54)可以反映出来,转动自由度主要影响横向剪切波与横波的频散方程. ...
... [28 ]更窄,高频的频率带隙基本一致. 对于纵波,两个模型均具有3条频散曲线,且相互重合,频率带隙基本一致. 横向旋转波与横波同Misra模型所预测存在差异,而其他形式的波基本一致,主要因为本文所建议模型多考虑了一个独立的转动自由度,因而具备了一个考虑转动的变形模式,通过式(52)~式(54)可以反映出来,转动自由度主要影响横向剪切波与横波的频散方程. ...
... 图5 所示为所建议模型预测频率带隙的宽度. 从图中可以看到,综合考虑横向剪切波、横向旋转波、横波与纵波的频散曲线,存在两个狭长带(图中红色与蓝色阴影区域),无论波数如何变化,期间均无任何频率的波能够在此介质传播,即此介质的频率带隙为5.13 × 1 0 6 ~ 5.74 × 1 0 6 6 ~ 6.86 × 1 0 6 [28 ] 预测的频率带隙,总体上,频率带隙的宽度相一致,但横波的频率带隙的宽度,本文建议模型所预测要窄于Misra模型,这还是由于所建议模型具有多考虑转动的变形模式的存在所引起的. ...
... (1)所建议模型能够模拟频散现象. 由于纵波、横波、横向剪切波、横向旋转波的频散关系分别受宏-细观尺度上的与平动项与转动项相关的参数的影响,其频散曲线各不相同. 横向剪切波具有1条平直的频散曲线;横向旋转波具有1条平直的频散曲线与1条呈双曲线衰减型频散曲线;纵波具有3条频散曲线,且与Misra [28 ] 所预测的频散曲线基本重合;由于所建议模型具有考虑了转动自由度的变形模式,横波具有四条频散曲线,比Misra [28 ] 所预测的多出一条低频的呈线性增长的频散曲线,另外3条变化规律相似且其中一条频散曲线基本重合. ...
... [28 ]所预测的多出一条低频的呈线性增长的频散曲线,另外3条变化规律相似且其中一条频散曲线基本重合. ...
Micro-structure in linear elasticity
8
1964
... 微形态理论[28 ,29 ,30 ,31 ,32 ,33 ] 同样具有描述复杂微结构变形的能力,可以被用于模拟颗粒材料. Misra [28 ] 根据Mindlin[29 ] 和Eringen[30 ] 的微结构线弹性理论建议了基于细观力学方法的颗粒材料微形态模型. 微形态理论假设物体是由宏观物质与细观物质组成的变形协调体,其每个物质点都是一个微结构胞元,并且引入9个变形自由度用以描述微结构的变形与旋转,适用于复杂微结构的变形模拟. 针对颗粒材料Misra等 [28 ] 认为一个物质点即为一个颗粒集合体体积单元,将颗粒运动分解为宏观运动与细观运动两个部分,并基于细观变形能求和得到宏观变形能函数,再通过对宏观变形能求导构建基于细观结构信息表示的宏观本构关系. ...
... [29 ]和Eringen[30 ] 的微结构线弹性理论建议了基于细观力学方法的颗粒材料微形态模型. 微形态理论假设物体是由宏观物质与细观物质组成的变形协调体,其每个物质点都是一个微结构胞元,并且引入9个变形自由度用以描述微结构的变形与旋转,适用于复杂微结构的变形模拟. 针对颗粒材料Misra等 [28 ] 认为一个物质点即为一个颗粒集合体体积单元,将颗粒运动分解为宏观运动与细观运动两个部分,并基于细观变形能求和得到宏观变形能函数,再通过对宏观变形能求导构建基于细观结构信息表示的宏观本构关系. ...
... 近年来,基于颗粒材料冲击与波动响应特性的调控波传播行为的超材料设计引起了研究者的兴趣,为此研究者已开展了大量基于广义连续 体模型(高阶梯度模型或Cosserat连续体模型)的波动分析 [34-36 ] . 正如上文所述,Cosserat连续体模型因包含了可与细观上颗粒转动相关联的转动自由度以及能够反映一定细观结构的内禀特征长度,且相对 简单而受到颗粒材料研究领域的广泛关注[17 ,30 ,34 -35 ,37 ] . 但是Cosserat连续体仅能反映细观结构的刚体转 动 [35 ,38 ] ,考虑到颗粒材料细观结构或者中尺度结构上诸如拉压与剪切等其他变形 模式的重要性[39 ,40 ] , 因而,能够反映细观结构完整运动模式的微形态连续体模型 [29 ,38 ] 引起了研究者的重视[28 ,41 -43 ] . 一阶微形态连续体模型除了描述宏观运动的自由度外,还包含描述微/细观结构变形的自由度,因此在其框架下基于细观途径发展颗粒 材料连续体模型能在一阶梯度情况下为更多细观信息的均匀化提供对应的描述变量. ...
... 本文基于Mindlin-Eringen的微结构理论[29 ,30 ] 和Misra的微形态理论 [28 ] ,给出了一个颗粒材料的微形态连续体模型. 不仅对颗粒的平动进行分解,同时对颗粒转动也进行了分解:颗粒运动分解为宏观平均运动(平动与转动)和细观真实运动(平动与转动)两 部分,并认为颗粒的细观真实运动(平动与转动)是由宏观平均运动(平动与转动)与相对运动(平动与转动)组成. 基于此分解,求得相应的细观本构关系和细观变形能函数. 结合宏观变形能的细观变形能求和表达式与细观本构关系的表达式,可获得基于细观量表示的宏观本构关系与相应的本构模量,其中包括了偶应力(相对偶应力)与微曲率(相对微曲率)的关系及其本构模量. 通过推导的微形态模型探讨波在弹性颗粒介质中传播的现象,考察纵波、横波、横向剪切波、横向旋转波的频散关系 [44 ] ,并对其频率带隙[44 ] 进行预测. ...
... 根据Mindlin的微结构理论 [29 ] ,建立一个全局坐标系 x V V P 图1 所示. 然后在 P x ' x ' x 图1 . 考虑 V p q p q [28 ] ...
... 式中, ϕ i l j p q ϕ i x ' x t 29 ]
... 同时,根据Mindlin的微结构理论[29 ] ,求得动能的变分为 ...
... 其中, d ρ ρ ' [29 ] ...
Microcontinuum Field Theories: Foundations and Solids
4
1999
... 微形态理论[28 ,29 ,30 ,31 ,32 ,33 ] 同样具有描述复杂微结构变形的能力,可以被用于模拟颗粒材料. Misra [28 ] 根据Mindlin[29 ] 和Eringen[30 ] 的微结构线弹性理论建议了基于细观力学方法的颗粒材料微形态模型. 微形态理论假设物体是由宏观物质与细观物质组成的变形协调体,其每个物质点都是一个微结构胞元,并且引入9个变形自由度用以描述微结构的变形与旋转,适用于复杂微结构的变形模拟. 针对颗粒材料Misra等 [28 ] 认为一个物质点即为一个颗粒集合体体积单元,将颗粒运动分解为宏观运动与细观运动两个部分,并基于细观变形能求和得到宏观变形能函数,再通过对宏观变形能求导构建基于细观结构信息表示的宏观本构关系. ...
... [30 ]的微结构线弹性理论建议了基于细观力学方法的颗粒材料微形态模型. 微形态理论假设物体是由宏观物质与细观物质组成的变形协调体,其每个物质点都是一个微结构胞元,并且引入9个变形自由度用以描述微结构的变形与旋转,适用于复杂微结构的变形模拟. 针对颗粒材料Misra等 [28 ] 认为一个物质点即为一个颗粒集合体体积单元,将颗粒运动分解为宏观运动与细观运动两个部分,并基于细观变形能求和得到宏观变形能函数,再通过对宏观变形能求导构建基于细观结构信息表示的宏观本构关系. ...
... 近年来,基于颗粒材料冲击与波动响应特性的调控波传播行为的超材料设计引起了研究者的兴趣,为此研究者已开展了大量基于广义连续 体模型(高阶梯度模型或Cosserat连续体模型)的波动分析 [34-36 ] . 正如上文所述,Cosserat连续体模型因包含了可与细观上颗粒转动相关联的转动自由度以及能够反映一定细观结构的内禀特征长度,且相对 简单而受到颗粒材料研究领域的广泛关注[17 ,30 ,34 -35 ,37 ] . 但是Cosserat连续体仅能反映细观结构的刚体转 动 [35 ,38 ] ,考虑到颗粒材料细观结构或者中尺度结构上诸如拉压与剪切等其他变形 模式的重要性[39 ,40 ] , 因而,能够反映细观结构完整运动模式的微形态连续体模型 [29 ,38 ] 引起了研究者的重视[28 ,41 -43 ] . 一阶微形态连续体模型除了描述宏观运动的自由度外,还包含描述微/细观结构变形的自由度,因此在其框架下基于细观途径发展颗粒 材料连续体模型能在一阶梯度情况下为更多细观信息的均匀化提供对应的描述变量. ...
... 本文基于Mindlin-Eringen的微结构理论[29 ,30 ] 和Misra的微形态理论 [28 ] ,给出了一个颗粒材料的微形态连续体模型. 不仅对颗粒的平动进行分解,同时对颗粒转动也进行了分解:颗粒运动分解为宏观平均运动(平动与转动)和细观真实运动(平动与转动)两 部分,并认为颗粒的细观真实运动(平动与转动)是由宏观平均运动(平动与转动)与相对运动(平动与转动)组成. 基于此分解,求得相应的细观本构关系和细观变形能函数. 结合宏观变形能的细观变形能求和表达式与细观本构关系的表达式,可获得基于细观量表示的宏观本构关系与相应的本构模量,其中包括了偶应力(相对偶应力)与微曲率(相对微曲率)的关系及其本构模量. 通过推导的微形态模型探讨波在弹性颗粒介质中传播的现象,考察纵波、横波、横向剪切波、横向旋转波的频散关系 [44 ] ,并对其频率带隙[44 ] 进行预测. ...
A unifying perspective: the relaxed linear micromorphic continuum
1
2014
... 微形态理论[28 ,29 ,30 ,31 ,32 ,33 ] 同样具有描述复杂微结构变形的能力,可以被用于模拟颗粒材料. Misra [28 ] 根据Mindlin[29 ] 和Eringen[30 ] 的微结构线弹性理论建议了基于细观力学方法的颗粒材料微形态模型. 微形态理论假设物体是由宏观物质与细观物质组成的变形协调体,其每个物质点都是一个微结构胞元,并且引入9个变形自由度用以描述微结构的变形与旋转,适用于复杂微结构的变形模拟. 针对颗粒材料Misra等 [28 ] 认为一个物质点即为一个颗粒集合体体积单元,将颗粒运动分解为宏观运动与细观运动两个部分,并基于细观变形能求和得到宏观变形能函数,再通过对宏观变形能求导构建基于细观结构信息表示的宏观本构关系. ...
The relaxed linear micromorphic continuum: Existence, uniqueness and continuous dependence in dynamics
1
2015
... 微形态理论[28 ,29 ,30 ,31 ,32 ,33 ] 同样具有描述复杂微结构变形的能力,可以被用于模拟颗粒材料. Misra [28 ] 根据Mindlin[29 ] 和Eringen[30 ] 的微结构线弹性理论建议了基于细观力学方法的颗粒材料微形态模型. 微形态理论假设物体是由宏观物质与细观物质组成的变形协调体,其每个物质点都是一个微结构胞元,并且引入9个变形自由度用以描述微结构的变形与旋转,适用于复杂微结构的变形模拟. 针对颗粒材料Misra等 [28 ] 认为一个物质点即为一个颗粒集合体体积单元,将颗粒运动分解为宏观运动与细观运动两个部分,并基于细观变形能求和得到宏观变形能函数,再通过对宏观变形能求导构建基于细观结构信息表示的宏观本构关系. ...
The relaxed linear micromorphic continuum: Well-posedness of the static problem and relations to the gauge theory of dislocations
1
2015
... 微形态理论[28 ,29 ,30 ,31 ,32 ,33 ] 同样具有描述复杂微结构变形的能力,可以被用于模拟颗粒材料. Misra [28 ] 根据Mindlin[29 ] 和Eringen[30 ] 的微结构线弹性理论建议了基于细观力学方法的颗粒材料微形态模型. 微形态理论假设物体是由宏观物质与细观物质组成的变形协调体,其每个物质点都是一个微结构胞元,并且引入9个变形自由度用以描述微结构的变形与旋转,适用于复杂微结构的变形模拟. 针对颗粒材料Misra等 [28 ] 认为一个物质点即为一个颗粒集合体体积单元,将颗粒运动分解为宏观运动与细观运动两个部分,并基于细观变形能求和得到宏观变形能函数,再通过对宏观变形能求导构建基于细观结构信息表示的宏观本构关系. ...
Enhanced micropolar model for wave propagation in ordered granular materials
2
2017
... 近年来,基于颗粒材料冲击与波动响应特性的调控波传播行为的超材料设计引起了研究者的兴趣,为此研究者已开展了大量基于广义连续 体模型(高阶梯度模型或Cosserat连续体模型)的波动分析 [34-36 ] . 正如上文所述,Cosserat连续体模型因包含了可与细观上颗粒转动相关联的转动自由度以及能够反映一定细观结构的内禀特征长度,且相对 简单而受到颗粒材料研究领域的广泛关注[17 ,30 ,34 -35 ,37 ] . 但是Cosserat连续体仅能反映细观结构的刚体转 动 [35 ,38 ] ,考虑到颗粒材料细观结构或者中尺度结构上诸如拉压与剪切等其他变形 模式的重要性[39 ,40 ] , 因而,能够反映细观结构完整运动模式的微形态连续体模型 [29 ,38 ] 引起了研究者的重视[28 ,41 -43 ] . 一阶微形态连续体模型除了描述宏观运动的自由度外,还包含描述微/细观结构变形的自由度,因此在其框架下基于细观途径发展颗粒 材料连续体模型能在一阶梯度情况下为更多细观信息的均匀化提供对应的描述变量. ...
... 图3 分别给出了表示横向剪切波、横向旋转波、横波与纵波的频散曲线. 从图3 (a)可以看到,对于横向剪切波来讲,只有一条呈平直的光波型的频散曲线,在本文参数取值下, 无论波数为多大,频率始终为 6.86 × 1 0 6 6.86 × 1 0 6 图3 (b)中,横向旋转波也具有一条呈平直的光波型的频散曲线,保持频率为 5.74 × 1 0 6 5.74 × 1 0 6 ~ 77.5 rad/s的横向旋转波能够传递. 从图3 (c)可以看到,横波具有四条频散曲线:第1条为低频线性增长的声波,最后达到 7.26 × 1 0 5 4.46 × 1 0 6 5.74 × 1 0 6 6.34 × 1 0 6 6.86 × 1 0 6 6 ~ 5.74 × 1 0 6 6 ~ 6.86 × 1 0 6 图3 (d),具有3条频散曲线,除不存在低频的曲线外,其变化规律与横波基本相同:第1条频散曲线达到稳定频率 5.13 × 1 0 6 6.86 × 1 0 6 7.75 × 1 0 6 8.19 × 1 0 6 6 ~ 6.86 × 1 0 6 6 ~ 8.19 × 1 0 6 ~ [34 ,48 -49 ] 证实六方密排结构中横向旋转波与频率带隙的 存在. ...
Mechanics of Generalized Continua: One Hundred Years After the Cosserats. Berlin, Heidelerg:
2
2010
... 近年来,基于颗粒材料冲击与波动响应特性的调控波传播行为的超材料设计引起了研究者的兴趣,为此研究者已开展了大量基于广义连续 体模型(高阶梯度模型或Cosserat连续体模型)的波动分析 [34-36 ] . 正如上文所述,Cosserat连续体模型因包含了可与细观上颗粒转动相关联的转动自由度以及能够反映一定细观结构的内禀特征长度,且相对 简单而受到颗粒材料研究领域的广泛关注[17 ,30 ,34 -35 ,37 ] . 但是Cosserat连续体仅能反映细观结构的刚体转 动 [35 ,38 ] ,考虑到颗粒材料细观结构或者中尺度结构上诸如拉压与剪切等其他变形 模式的重要性[39 ,40 ] , 因而,能够反映细观结构完整运动模式的微形态连续体模型 [29 ,38 ] 引起了研究者的重视[28 ,41 -43 ] . 一阶微形态连续体模型除了描述宏观运动的自由度外,还包含描述微/细观结构变形的自由度,因此在其框架下基于细观途径发展颗粒 材料连续体模型能在一阶梯度情况下为更多细观信息的均匀化提供对应的描述变量. ...
... [35 ,38 ],考虑到颗粒材料细观结构或者中尺度结构上诸如拉压与剪切等其他变形 模式的重要性[39 ,40 ] , 因而,能够反映细观结构完整运动模式的微形态连续体模型 [29 ,38 ] 引起了研究者的重视[28 ,41 -43 ] . 一阶微形态连续体模型除了描述宏观运动的自由度外,还包含描述微/细观结构变形的自由度,因此在其框架下基于细观途径发展颗粒 材料连续体模型能在一阶梯度情况下为更多细观信息的均匀化提供对应的描述变量. ...
Gradient elasticity in statics and dynamics: An overview of formulations, length scale identification procedures, finite element implementations and new results
2011
Dispersion and wave propagation in discrete and continuous models for granular materials
1
1996
... 近年来,基于颗粒材料冲击与波动响应特性的调控波传播行为的超材料设计引起了研究者的兴趣,为此研究者已开展了大量基于广义连续 体模型(高阶梯度模型或Cosserat连续体模型)的波动分析 [34-36 ] . 正如上文所述,Cosserat连续体模型因包含了可与细观上颗粒转动相关联的转动自由度以及能够反映一定细观结构的内禀特征长度,且相对 简单而受到颗粒材料研究领域的广泛关注[17 ,30 ,34 -35 ,37 ] . 但是Cosserat连续体仅能反映细观结构的刚体转 动 [35 ,38 ] ,考虑到颗粒材料细观结构或者中尺度结构上诸如拉压与剪切等其他变形 模式的重要性[39 ,40 ] , 因而,能够反映细观结构完整运动模式的微形态连续体模型 [29 ,38 ] 引起了研究者的重视[28 ,41 -43 ] . 一阶微形态连续体模型除了描述宏观运动的自由度外,还包含描述微/细观结构变形的自由度,因此在其框架下基于细观途径发展颗粒 材料连续体模型能在一阶梯度情况下为更多细观信息的均匀化提供对应的描述变量. ...
Analysis of plane Couette shear test of granular media in a Cosserat continuum approach
2
2014
... 近年来,基于颗粒材料冲击与波动响应特性的调控波传播行为的超材料设计引起了研究者的兴趣,为此研究者已开展了大量基于广义连续 体模型(高阶梯度模型或Cosserat连续体模型)的波动分析 [34-36 ] . 正如上文所述,Cosserat连续体模型因包含了可与细观上颗粒转动相关联的转动自由度以及能够反映一定细观结构的内禀特征长度,且相对 简单而受到颗粒材料研究领域的广泛关注[17 ,30 ,34 -35 ,37 ] . 但是Cosserat连续体仅能反映细观结构的刚体转 动 [35 ,38 ] ,考虑到颗粒材料细观结构或者中尺度结构上诸如拉压与剪切等其他变形 模式的重要性[39 ,40 ] , 因而,能够反映细观结构完整运动模式的微形态连续体模型 [29 ,38 ] 引起了研究者的重视[28 ,41 -43 ] . 一阶微形态连续体模型除了描述宏观运动的自由度外,还包含描述微/细观结构变形的自由度,因此在其框架下基于细观途径发展颗粒 材料连续体模型能在一阶梯度情况下为更多细观信息的均匀化提供对应的描述变量. ...
... ,38 ]引起了研究者的重视[28 ,41 -43 ] . 一阶微形态连续体模型除了描述宏观运动的自由度外,还包含描述微/细观结构变形的自由度,因此在其框架下基于细观途径发展颗粒 材料连续体模型能在一阶梯度情况下为更多细观信息的均匀化提供对应的描述变量. ...
Mesoscale measures of nonaffine deformation in dense granular assemblies
1
2008
... 近年来,基于颗粒材料冲击与波动响应特性的调控波传播行为的超材料设计引起了研究者的兴趣,为此研究者已开展了大量基于广义连续 体模型(高阶梯度模型或Cosserat连续体模型)的波动分析 [34-36 ] . 正如上文所述,Cosserat连续体模型因包含了可与细观上颗粒转动相关联的转动自由度以及能够反映一定细观结构的内禀特征长度,且相对 简单而受到颗粒材料研究领域的广泛关注[17 ,30 ,34 -35 ,37 ] . 但是Cosserat连续体仅能反映细观结构的刚体转 动 [35 ,38 ] ,考虑到颗粒材料细观结构或者中尺度结构上诸如拉压与剪切等其他变形 模式的重要性[39 ,40 ] , 因而,能够反映细观结构完整运动模式的微形态连续体模型 [29 ,38 ] 引起了研究者的重视[28 ,41 -43 ] . 一阶微形态连续体模型除了描述宏观运动的自由度外,还包含描述微/细观结构变形的自由度,因此在其框架下基于细观途径发展颗粒 材料连续体模型能在一阶梯度情况下为更多细观信息的均匀化提供对应的描述变量. ...
Kinematic variables bridging discrete and continuum granular mechanics
1
2006
... 近年来,基于颗粒材料冲击与波动响应特性的调控波传播行为的超材料设计引起了研究者的兴趣,为此研究者已开展了大量基于广义连续 体模型(高阶梯度模型或Cosserat连续体模型)的波动分析 [34-36 ] . 正如上文所述,Cosserat连续体模型因包含了可与细观上颗粒转动相关联的转动自由度以及能够反映一定细观结构的内禀特征长度,且相对 简单而受到颗粒材料研究领域的广泛关注[17 ,30 ,34 -35 ,37 ] . 但是Cosserat连续体仅能反映细观结构的刚体转 动 [35 ,38 ] ,考虑到颗粒材料细观结构或者中尺度结构上诸如拉压与剪切等其他变形 模式的重要性[39 ,40 ] , 因而,能够反映细观结构完整运动模式的微形态连续体模型 [29 ,38 ] 引起了研究者的重视[28 ,41 -43 ] . 一阶微形态连续体模型除了描述宏观运动的自由度外,还包含描述微/细观结构变形的自由度,因此在其框架下基于细观途径发展颗粒 材料连续体模型能在一阶梯度情况下为更多细观信息的均匀化提供对应的描述变量. ...
Generalized micromorphic solids and fluids
1
2011
... 近年来,基于颗粒材料冲击与波动响应特性的调控波传播行为的超材料设计引起了研究者的兴趣,为此研究者已开展了大量基于广义连续 体模型(高阶梯度模型或Cosserat连续体模型)的波动分析 [34-36 ] . 正如上文所述,Cosserat连续体模型因包含了可与细观上颗粒转动相关联的转动自由度以及能够反映一定细观结构的内禀特征长度,且相对 简单而受到颗粒材料研究领域的广泛关注[17 ,30 ,34 -35 ,37 ] . 但是Cosserat连续体仅能反映细观结构的刚体转 动 [35 ,38 ] ,考虑到颗粒材料细观结构或者中尺度结构上诸如拉压与剪切等其他变形 模式的重要性[39 ,40 ] , 因而,能够反映细观结构完整运动模式的微形态连续体模型 [29 ,38 ] 引起了研究者的重视[28 ,41 -43 ] . 一阶微形态连续体模型除了描述宏观运动的自由度外,还包含描述微/细观结构变形的自由度,因此在其框架下基于细观途径发展颗粒 材料连续体模型能在一阶梯度情况下为更多细观信息的均匀化提供对应的描述变量. ...
Homogenization of a Cauchy continuum towards a micromorphic continuum
2017
Nonlinear regularization operators as a derived from the micromorphic approach to gradient elasticity, viscoplasticity and damage
1
2016
... 近年来,基于颗粒材料冲击与波动响应特性的调控波传播行为的超材料设计引起了研究者的兴趣,为此研究者已开展了大量基于广义连续 体模型(高阶梯度模型或Cosserat连续体模型)的波动分析 [34-36 ] . 正如上文所述,Cosserat连续体模型因包含了可与细观上颗粒转动相关联的转动自由度以及能够反映一定细观结构的内禀特征长度,且相对 简单而受到颗粒材料研究领域的广泛关注[17 ,30 ,34 -35 ,37 ] . 但是Cosserat连续体仅能反映细观结构的刚体转 动 [35 ,38 ] ,考虑到颗粒材料细观结构或者中尺度结构上诸如拉压与剪切等其他变形 模式的重要性[39 ,40 ] , 因而,能够反映细观结构完整运动模式的微形态连续体模型 [29 ,38 ] 引起了研究者的重视[28 ,41 -43 ] . 一阶微形态连续体模型除了描述宏观运动的自由度外,还包含描述微/细观结构变形的自由度,因此在其框架下基于细观途径发展颗粒 材料连续体模型能在一阶梯度情况下为更多细观信息的均匀化提供对应的描述变量. ...
声光子晶体带隙特性与声光耦合作用研究综述
2
2017
... 本文基于Mindlin-Eringen的微结构理论[29 ,30 ] 和Misra的微形态理论 [28 ] ,给出了一个颗粒材料的微形态连续体模型. 不仅对颗粒的平动进行分解,同时对颗粒转动也进行了分解:颗粒运动分解为宏观平均运动(平动与转动)和细观真实运动(平动与转动)两 部分,并认为颗粒的细观真实运动(平动与转动)是由宏观平均运动(平动与转动)与相对运动(平动与转动)组成. 基于此分解,求得相应的细观本构关系和细观变形能函数. 结合宏观变形能的细观变形能求和表达式与细观本构关系的表达式,可获得基于细观量表示的宏观本构关系与相应的本构模量,其中包括了偶应力(相对偶应力)与微曲率(相对微曲率)的关系及其本构模量. 通过推导的微形态模型探讨波在弹性颗粒介质中传播的现象,考察纵波、横波、横向剪切波、横向旋转波的频散关系 [44 ] ,并对其频率带隙[44 ] 进行预测. ...
... [44 ]进行预测. ...
声光子晶体带隙特性与声光耦合作用研究综述
2
2017
... 本文基于Mindlin-Eringen的微结构理论[29 ,30 ] 和Misra的微形态理论 [28 ] ,给出了一个颗粒材料的微形态连续体模型. 不仅对颗粒的平动进行分解,同时对颗粒转动也进行了分解:颗粒运动分解为宏观平均运动(平动与转动)和细观真实运动(平动与转动)两 部分,并认为颗粒的细观真实运动(平动与转动)是由宏观平均运动(平动与转动)与相对运动(平动与转动)组成. 基于此分解,求得相应的细观本构关系和细观变形能函数. 结合宏观变形能的细观变形能求和表达式与细观本构关系的表达式,可获得基于细观量表示的宏观本构关系与相应的本构模量,其中包括了偶应力(相对偶应力)与微曲率(相对微曲率)的关系及其本构模量. 通过推导的微形态模型探讨波在弹性颗粒介质中传播的现象,考察纵波、横波、横向剪切波、横向旋转波的频散关系 [44 ] ,并对其频率带隙[44 ] 进行预测. ...
... [44 ]进行预测. ...
Incorporating rolling resistance and contact anisotropy in micromechanical models of granular media
1
2002
... 其中, τ ij σ ij μ ij ν ij [45 ] 认为颗粒材料的宏观变形能密度为颗粒接触间的细观变形能密度 w w w = w δ i M , δ i m , δ i R , θ i R , θ i s , θ i u . 那么,整个体积元的 V
Elastic model for partially saturated granular materials
3
2008
... 为建立颗粒的细观本构关系,首先对一个颗粒接触对建立局部坐标系,如图2 所示[46 ] . 向量 n s t
... 颗粒接触的局部坐标[46 ] ...
... Local coordinate system at a contact of particles[46 ] ...
Elastic material constants for isotropic granular solids with particle rotation
1
1992
... 从式(29) ~ V [47 ] 提出了一个方向分布密度函数 ξ ξ α , β = 1 / 4 π
Dispersion of elastic waves in three-dimensional noncohesive granular phononic crystals: properties of rotational modes
1
2010
... 图3 分别给出了表示横向剪切波、横向旋转波、横波与纵波的频散曲线. 从图3 (a)可以看到,对于横向剪切波来讲,只有一条呈平直的光波型的频散曲线,在本文参数取值下, 无论波数为多大,频率始终为 6.86 × 1 0 6 6.86 × 1 0 6 图3 (b)中,横向旋转波也具有一条呈平直的光波型的频散曲线,保持频率为 5.74 × 1 0 6 5.74 × 1 0 6 ~ 77.5 rad/s的横向旋转波能够传递. 从图3 (c)可以看到,横波具有四条频散曲线:第1条为低频线性增长的声波,最后达到 7.26 × 1 0 5 4.46 × 1 0 6 5.74 × 1 0 6 6.34 × 1 0 6 6.86 × 1 0 6 6 ~ 5.74 × 1 0 6 6 ~ 6.86 × 1 0 6 图3 (d),具有3条频散曲线,除不存在低频的曲线外,其变化规律与横波基本相同:第1条频散曲线达到稳定频率 5.13 × 1 0 6 6.86 × 1 0 6 7.75 × 1 0 6 8.19 × 1 0 6 6 ~ 6.86 × 1 0 6 6 ~ 8.19 × 1 0 6 ~ [34 ,48 -49 ] 证实六方密排结构中横向旋转波与频率带隙的 存在. ...
Experimental evidence of rotational elastic waves in granular phononic crystals
1
2011
... 图3 分别给出了表示横向剪切波、横向旋转波、横波与纵波的频散曲线. 从图3 (a)可以看到,对于横向剪切波来讲,只有一条呈平直的光波型的频散曲线,在本文参数取值下, 无论波数为多大,频率始终为 6.86 × 1 0 6 6.86 × 1 0 6 图3 (b)中,横向旋转波也具有一条呈平直的光波型的频散曲线,保持频率为 5.74 × 1 0 6 5.74 × 1 0 6 ~ 77.5 rad/s的横向旋转波能够传递. 从图3 (c)可以看到,横波具有四条频散曲线:第1条为低频线性增长的声波,最后达到 7.26 × 1 0 5 4.46 × 1 0 6 5.74 × 1 0 6 6.34 × 1 0 6 6.86 × 1 0 6 6 ~ 5.74 × 1 0 6 6 ~ 6.86 × 1 0 6 图3 (d),具有3条频散曲线,除不存在低频的曲线外,其变化规律与横波基本相同:第1条频散曲线达到稳定频率 5.13 × 1 0 6 6.86 × 1 0 6 7.75 × 1 0 6 8.19 × 1 0 6 6 ~ 6.86 × 1 0 6 6 ~ 8.19 × 1 0 6 ~ [34 ,48 -49 ] 证实六方密排结构中横向旋转波与频率带隙的 存在. ...