力学学报 2018 , 50 (2): 297-306 https://doi.org/10.6052/0459-1879-17-378

Orginal Article

基于M积分的脆性材料微缺陷等效损伤面积/体积表征

朱文洁, 吕俊男, 李群

西安交通大学航天航空学院机械结构强度与振动国家重点实验室,西安 710049

THE CALIBRATION OF MICRODEFECTS INDUCED EQUIVALENT DAMAGE AREA/VOLUME OF BRITTLE MATERIALS BY USING THE M-INTEGRAL

Zhu Wenjie, Lü Junnan, Li Qun

State Key Laboratory for Strength and Vibration of Mechanical Structures, School of Aerospace, Xi’an Jiaotong University, Xi’an 710049, China

中图分类号: O346.1

文献标识码: A

收稿日期: 2017-11-14

接受日期: 2017-11-14

网络出版日期: 2018-04-17

基金资助: 国家自然科学基金面上项目(11472205, 11772245), 高等学校学科创新引智计划(B18040)和中央高校基本科研业务费资助.

作者简介:

作者简介：李群,教授,博士生导师,主要从事断裂与损伤力学研究. E-mail: qunli@mail.xjtu.edu.cn

展开

摘要

随着脆性材料在工程中的广泛应用,对脆性材料中微缺陷进行统一的损伤水平标定,具有重要的科学研究和工程应用价值. 本研究提出一种基于M积分的材料等效损伤面积/体积标定方法, 以具有相同M积分值的圆孔面积或球孔体积来标定复杂微缺陷构型的损伤水平,从而实现不同类型微缺陷真实损伤水平的统一表征. 首先,基于Lagrangian能量密度函数推导了M积分定义式,并简述了M积分的物理意义,基于域积分方法实现二维/三维M积分的数值计算. 随后,提出了基于M积分的材料缺陷等效损伤面积/体积标定方法,以圆孔面积/球孔体积来标定复杂微缺陷材料系统的损伤水平. 最后, 针对单轴拉伸载荷作用下的二维/三维脆性体含不同缺陷构型,具体计算了椭圆孔、裂纹以及双裂纹、双孔洞、裂纹和孔洞干涉等复杂缺陷构型情况下的等效损伤面积/体积,并详细分析了缺陷之间的干涉效应及影响因素. 本研究旨在基于M积分等效方法量化脆性材料中各类微缺陷造成的损伤程度,实现损伤等级标定,有益于工程材料及结构的损伤容限设计及完整性评估.

关键词： ; M积分 ; 等效损伤面积 ; 等效损伤体积 ; 干涉效应

Abstract

In view of the integrity, reliability and functionality of brittle materials are substantially limited by the existence of microdefects, the calibration of materials’ damage level is of great scientific value and underlying engineering applications. An unified method of evaluating the microdefects induced equivalent damage area/volume is proposed in present study by the aid of M-integral. The damage area/volume induced by underlying multiple microdefects is assumed as equivalent to the area/volume of an individual circular/spherical void while the values of M-integral are equal for the both cases. Firstly, the analytical expression of M-integral is deduced by using the Lagrangian energy density function, the corresponding physical meaning is briefly elucidated. The domain integral method is applied to numerically calculating the M-integral for both two-dimensional (2D) and three-dimensional (3D) cases. Subsequently, the damage calibration process of arbitrary dispersed microdefects is given, the corresponding equivalent damage area for 2D defects and volume for 3D defects are defined. Finally, the elastic 2D plane and 3D body under uniaxial tensile loading condition is simulated, within which a series of different defect configurations are considered, including the singular defect (void, crack and ellipse) and the dual-defects (void-void, crack-crack, void-crack). Corresponding equivalent damage area or volume are calculated, the inherent “interactive effects” and influence factors are elucidated detailedly and quantitatively. Through the proposed damage calibration method in this study, we can estimate the damage level of any microdefects within brittle solids, the calibration process is simple and convenient, which will be beneficial to the damage tolerance design and integrity assessment of engineering structures.

Keywords： microdefects ; M-integral ; equivalent damage area ; equivalent damage volume ; interaction effect

PDF (3211KB) 元数据多维度评价相关文章收藏文章

本文引用格式导出 EndNote Ris Bibtex

朱文洁, 吕俊男, 李群. 基于M积分的脆性材料微缺陷等效损伤面积/体积表征[J]. 力学学报, 2018, 50(2): 297-306 https://doi.org/10.6052/0459-1879-17-378

Zhu Wenjie, Lü Junnan, Li Qun. THE CALIBRATION OF MICRODEFECTS INDUCED EQUIVALENT DAMAGE AREA/VOLUME OF BRITTLE MATERIALS BY USING THE M-INTEGRAL[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(2): 297-306 https://doi.org/10.6052/0459-1879-17-378

引言

脆性材料(陶瓷、玻璃、混凝土、岩石等)广泛应用在机械、建筑等多个领域,其断裂失效常常起源于制造及服役过程中产生的缺陷 (裂纹、夹杂、孔洞等). 微缺陷的存在导致脆性结构服役过程中发生损伤演化. 针对脆性材料的多微缺陷致失效已经得到广泛研究^[1,2],其中涉及微裂纹扩展、微孔洞形核、聚合等^[3,4,5,6]. 微裂纹造成脆性材料不可逆的损伤,使得其强度、刚度等力学性能明显下降,进而会严重缩短材料的剩余使用寿命,对工程结构失效分析和强度校核带来了巨大挑战 ^[7]. 因此,对脆性材料中微缺陷进行统一的损伤水平标定,具有重要的科学研究和工程应用价值.

传统的缺陷标定大多基于直接观测法 ^[8],包括人工肉眼或使用放大镜观测缺陷,根据对缺陷进行分类,利用经验判断缺陷的损伤水平,或根据观测到的直观几何面积大小评定缺陷等级,但缺陷的直观几何面积与其造成的损伤水平(面积)并不直接呈正关系. 例如：裂纹类缺陷的几何面积近乎为零,这显然不匹配其实际造成的损伤水平;而几何面积相同的圆孔缺陷和椭圆孔缺陷对材料造成的损伤也有很大差别 ^[9]. 总体来说,缺陷对材料的损伤水平一般为裂纹大于椭圆孔,椭圆孔大于圆孔. 此外,对于复杂缺陷情况,缺陷数量巨大、尺寸不一、形态各异,使得人工分类、评估非常困难,而缺陷间的相互干涉效应也无法表征. 因此,传统的人工标定方法已经不能适应现代工业生产对缺陷检测分析和评估的要求.

目前应用较多的缺陷质量分级办法中还包括无损检测标定方法,选择适宜的无损检测技术后,针对于不同类型的缺陷采用不同的质量分级办法. 徐真军等 ^[10]针对长宽比大于3的“条形缺陷”通过规定在待评定区长度和相邻缺陷距离内,任意一组“条形缺陷”的累计长度范围来划分等级,在不同类型缺陷评定质量级别不同时,以质量最差的级别作为其真实质量等级. 汪孝欢等 ^[11]针对长宽比不大于3的“圆形缺陷”,在缺陷最严重的区域根据母材尺寸选择相应的缺陷评定区,根据每个级别在各评定区尺寸所允许的圆形缺陷点数表格来划分质量等级. 实际工程中,存在很多不规则的缺陷,为了应用断裂力学分析缺陷,往往将它们处理成规范性裂纹,即半椭圆裂纹、椭圆埋藏裂纹、穿透裂纹,但这种简化过程不完全符合实际情况,很难保证其准确性. 总体来说,基于不同的缺陷检测方法以及针对不同类型缺陷使用的质量分级办法,各类缺陷对材料造成的损伤水平无法进行统一评估标定,且多数质量分级根据经验划分. 目前,尚缺乏一种适用于各类受检物、复杂缺陷的材料真实损伤面积标定方法.

当材料中的缺陷的构型(形状和位置)改变时,会引起材料自由能的变化. 与材料的构型变化相关的驱动力定义为构型力,又称“材料力”. 关于构型力的概念可以追溯到Eshelby等 ^[12]于1951年提出的能量动量张量概念,其物理意义可解释为单位厚度的无限小单元沿坐标轴平移所对应的势能变化量. 近年来,许多研究学者发现材料构型力学理论体系在描述含缺陷材料或构件的破坏行为方面具有得天独厚的优势^{[13,14,15,16,17,18,19,20]}. 其中,M积分作为材料构型力学理论体系的重要守恒积分,已广泛应用于断裂、损伤以及缺陷识别领域.^[6,21]基于有限元分析,系统研究了裂纹、孔洞缺陷在发生聚合前后,M积分的变化规律及其与材料有效弹性模量之间的内在联系,其认为M 积分值在缺陷聚合(干涉效应)时所发生的“跳跃”表明材料的损伤水平进一步加深. 另外,近年来,许多学者提出M 积分可以用来描述含复杂缺陷材料的破坏行为. 代表性的工作有,于宁宇等 ^[22] 的研究表明M积分不但可以表征材料构型上的不连续性,也能表征材料的非线性弹塑性行为. 远端载荷、材料行为以及缺陷构型对 M积分的影响表明M积分在描述材料的微缺陷损伤中具有重要作用. 随后又基于M 积分提出了新的统一失效准则 ^[23],该准则采用无量纲参数来表征材料的损伤水平,并假定当损伤累积到一个门槛值时, 材料发生失效. 随后,Li等 ^[24]基于数字图像相关技术,研究了含局部复杂缺陷的LY-12铝合金板(“十字形”试样)受双轴载荷作用下的失效行为,实验测得合金板的临界损伤参数,验证了该参数适用于含复杂缺陷、受复杂载荷作用的弹--塑性材料的失效评价. Goldstein等 ^[25]应用包括M 积分在内的守恒积分(J,M,L积分),结合简单的含球形孔/夹杂试件的单轴拉伸实验,对材料内部球形缺陷的半径、弹性模量及中心坐标进行了准确预测. Gommerstadt ^[26]应用M 积分以及J-积分,研究了含孔洞缺陷的固体受时域谐波激励作用发生振动失效的弹性动力学问题,并指出M 积分在无损检测中的潜在应用. 最近,Meyer 等 ^[27]应用M 积分研究了冰川下的排水通道的蠕变损伤闭合效应. 基于以上研究,M 积分的物理意义可以理解为当前构型与无任何缺陷构型之间,各个缺陷表面的质点均以自相似扩展方式达到当前构型时,两种构型的总势能变化,其代表着材料整体缺陷发生自相似扩展导致的能量释放率 ^[28],可应用于材料和结构的缺陷损伤标定.

综上所述,M 积分对含不同类型缺陷的材料系统进行损伤标定已引起广泛关注. 另外,传统缺陷质量分级评定办法,根据缺陷直观几何面积估计损伤水平,以及对于各类不规则缺陷经过简化后分类进行质量分级评定,或使用传统断裂力学知识分析缺陷构型,都无法反应缺陷真实损伤水平,且没有考虑缺陷干涉的影响. 基于此,本工作应用M 积分的优良特性及其明确的物理意义,提出一种基于M 积分的材料等效损伤面积/体积标定方法,提出复杂微缺陷构型的损伤水平以具有相同M 积分值的圆孔面积或球孔体积来标定,从而实现不同类型微缺陷真实损伤水平的统一表征. 相较于传统的缺陷质量分级评定办法,本方法可以用来标定各类缺陷损伤水平,该方法更符合材料中缺陷的实际情况,可为工程结构的剩余强度设计及完整性评估提供依据.

1 M 积分的定义及其数值计算

1.1 M 积分定义

本节将通过Lagrangian能量密度函数推导得到M 积分,固体材料质点的Lagrangian能量密度函数 $\bar{L}$ 可以看作坐标、位移以及应变张量的函数. 如果不考虑惯性项,则Lagrangian能量密度函数 $\bar{L}$ 可以定义为

$\begin{array}{l} \bar{L} = \bar{L} (x_{i}, u_{k} (x_{i}), ε_{kj} (x_{i})) = - V (x_{i}, u_{k} (x_{i})) - w (x_{i}, ε_{kj} (x_{i})) \end{array}$ (1)

其中, $V$ 代表体力势; $w$ 代表应变能密度.

通过对Lagrangian能量动量函数的散度运算可以得到与守恒M 积分相关的构型力. 不考虑体力造成的影响,即体力势 $V = 0$ ,此时Lagrangian能量动量函数的散度可以表示为

$\begin{array}{l} \nabla \cdot (\bar{L} x) = (w x_{i})_{, i} = mw + {(\frac{\partial w}{\partial x_{i}})}_{expl} x_{i} + \frac{\partial w}{\partial u_{k}} u_{k, i} x_{i} + \frac{\partial w}{\partial u_{k, j}} u_{k, ji} x_{i} \end{array}$ (2)

其中, $x_{i}$ 为质点坐标; $u_{i}$ 为位移分量; $w$ 为应变能密度函数;下标 ${}_{, j}$ 表示相应物理量对坐标 $x_{j}$ 的偏导数;( $\partial w / \partial x_{i})_{expl .}$ 表示应变能密度 $w$ 关于坐标 $x_{i}$ 的显式偏导数;参数 $m = x_{i, i}$ 是与维度相关的变量,二维问题中 $m = 2$ ,对于三维问题来说 $m = 3$ .

从应变能密度中的柯西应力张量定义及其对称性,可得

$σ_{kj} = σ_{jk} = \frac{\partial w}{\partial ε_{kj}} = \frac{\partial w}{\partial u_{k, j}}$ (3)

其中,材料的几何方程为

$ε_{kj} = \frac{1}{2} (u_{k, j} + u_{j, k})$ (4)

通过式(3)与式(4),式(2)可以整理为

$(w x_{i})_{, i} = mw + (\frac{\partial w}{\partial x_{i}})_{expl .} x_{i} + σ_{jk} u_{k, ji} x_{i}$ (5)

利用平衡方程 $σ_{kj, j} + f_{k} = 0$ , 式(5)等号右侧第三项可以写成

$σ_{jk} u_{k, ji} x_{i} = (σ_{jk} u_{k, i} x_{i})_{, j} - σ_{jk, j} u_{k, i} x_{i} - σ_{jk} u_{k, i} x_{i, j} = (σ_{jk} u_{k, i} x_{i})_{, j} - σ_{jk} u_{k, j}$ (6)

通过式(5)和式(6),有

$(w x_{i} δ_{ij} - σ_{jk} u_{k, i} x_{i})_{, j} = mw - σ_{jk} u_{k, j} + (\frac{\partial w}{\partial x_{i}})_{e xpl} x_{i}$ (7)

其中, $δ_{ij}$ 为Kronecker符号. 利用应变能密度定义式 $w = \frac{1}{2} σ_{ij} ε_{ij} = \frac{1}{2} σ_{ij} u_{i, j}$ ,将式(7)重新整理,得到

$(w x_{i} δ_{ij} - σ_{jk} u_{k, i} x_{i} + 2 - m 2 σ_{jk} u_{k})_{, j} = (\partial w \partial x_{i})_{expl} x_{i}$ (8)

由式(8)可以得到与M 积分相关的构型应力分量与构型力

$M_{j} = w x_{i} δ_{ij} - σ_{jk} u_{k, i} x_{i} + \frac{2 - m}{2} σ_{jk} u_{k}$ (9)

$Λ = - (\frac{\partial w}{\partial x_{i}})_{expl} x_{i}$ (10)

其中, $M_{j}$ 可以看做是材料自相似扩展构型应力; $Λ$ 代表自相似扩展构型力,可以视作材料“损伤源”项,由材料的非均质特性导致. 式(9)和式(10)满足平衡关系 $M_{j, j} + Λ = 0$ (11)

M 积分可以通过自相似扩展构型应力 $M_{j}$ 沿着包含所有缺陷的任意闭合积分路径进行积分得到

$\begin{array}{l} M = \int_{S} ‍ M_{j} n_{j} dA = \int_{S} ‍ (w x_{i} δ_{ij} - σ_{jk} u_{k, i} x_{i} + 2 - m 2 σ_{jk} u_{k}) n_{j} dA \end{array}$ (12)

而在二维问题中,此时式(12)中,与维度相关的参量 $m = 2$ ,M 积分为

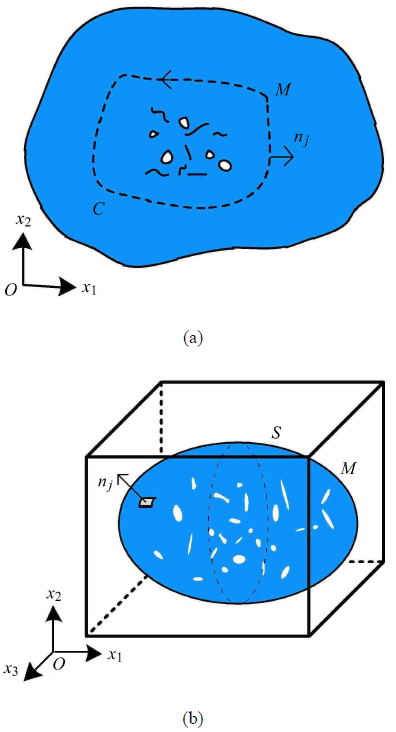
$M = \oint_{C} ‍ (w x_{j} - σ_{jk} u_{k, i} x_{i}) n_{j} dl$ (13)

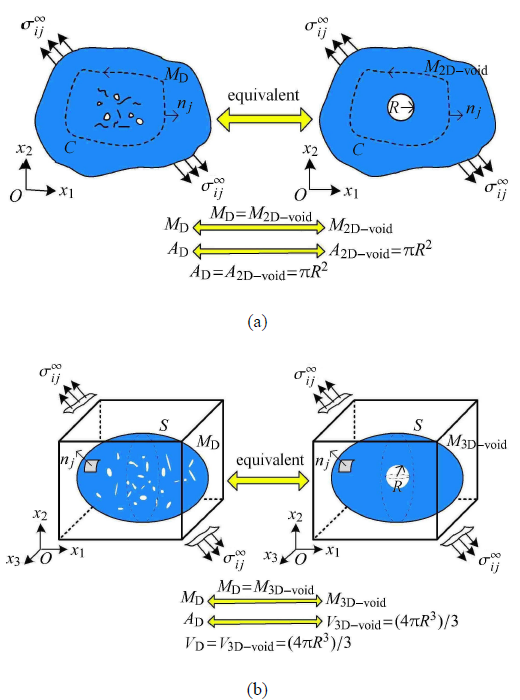
其中 $n_{j}$ 为围绕缺陷闭合积分路径 $C$ 的单位外法向矢量,如图1(a)所示.

在三维问题中,此时式(12)中,与维度相关的参量 $m = 3$ ,M 积分为

$M = \int_{S} ‍ (w x_{i} δ_{ij} - σ_{jk} u_{k, i} x_{i} - \frac{1}{2} σ_{jk} u_{k}) n_{j} dA$ (14)

其中 $n_{j}$ 为围绕缺陷闭合面积分路径 $S$ 的单位外法向矢量,如图1(b)所示.

M 积分的物理意义可以理解为当前构型与无任何缺陷的构型之间,当各个缺陷表面的质点均以自相似的扩展方式达到当前构型时, 两种构型的总势能变化. 在线弹性材料情况下,计算缺陷的M 积分时,只需将积分路径完全包围缺陷便可以进行计算,且M 积分是一种路径无关积分,其值不依赖积分路径的选取^[3,4]. 另外,对于奇异应力场主导的各类缺陷问题,在远离缺陷的区域(不需要特别精密的网格),M 积分值可以通过域积分法准确求解^[29,30,31],将在后文作详细介绍.

显示原图| 下载原图ZIP| 生成PPT

图1 (a) 二维M 积分示意图, (b)三维M 积分示意图

Fig. 1 Schematic diagram of integration curve of calculating the M integral for (a) two-dimensional plane and (b) three-dimensional body with multi-defects

1.2 基于域积分法的 M 积分数值计算

有限元数值计算方法在计算断裂参数中起到了重要的作用,本研究将采用域积分法对M 积分开展计算.

由于有限元数值计算M 积分需要计算经过积分曲线所有点的M 积分值,其计算结果只是近似的. 而因为场变量的存在,对裂纹尖端附近的区域进行计算则是较为精确的. 因此对于二维M 积分,可将其等效为面积分,即

$M = \oint_{C} ‍ (w x_{i} - σ_{ik} u_{k, i} x_{i}) n_{i} dl = \int_{S} ‍ M_{i} n_{i} dS$ (15)

引入弱函数 $q$ ,具有恒等式( $M_{i} q)_{i} = M_{i, i} q + M_{i} q_{, i}$ ,M 积分的计算对于假设的函数 $q$ 的形式并不敏感,因此函数 $q$ 可以任意选取. 给定 $q = x_{i}$ ,基于域积分法 ^[29,30,31]将M 积分转化为域积分后的形式为

$\begin{array}{l} M = - \int_{S} ‍ (M_{i, i} q + M_{i} q_{, i}) dS = \\ \int_{S} ‍ (- W x_{i} + σ_{ki} u_{k, j} x_{j}) \frac{\partial q}{\partial x_{i}} dS \end{array}$ (16)

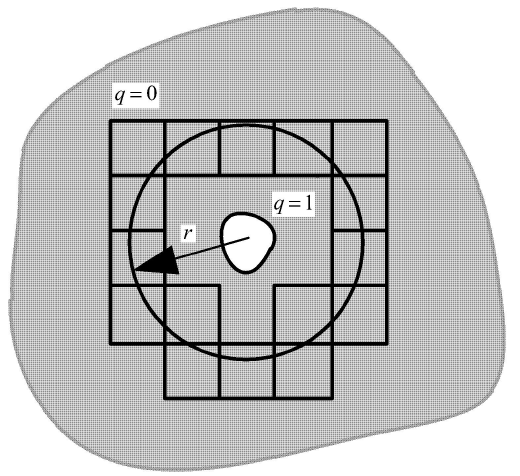
为了计算方便,积分区域的边界可以选在单元的边上. 函数 $q$ 满足在单元内满足形函数插值

$Q = N_{1} q_{1}^{e} + N_{2} q_{2}^{e} + N_{3} q_{3}^{e} + N_{4} q_{4}^{e} = \sum_{i=1}^{4} ‍ N_{i} (r, s) q_{i}^{e}$ (17)

其中 $N$ 代表形函数, ( $r, s$ )为高斯点坐标.

在某个单元内的M 积分可用下式计算

$M^{e} = \int_{-}^{1} ‍ \int_{-}^{1} ‍ I (r, s) drds$ (18)

其中

$\begin{array}{l} I (r, s) = [(σ_{xx} \partial u \partial xx + σ_{xx} \partial u \partial yy + τ_{xy} \partial v \partial xx + \\ τ_{xy} \partial v \partial xx - Wx) \partial q \partial x + \\ (τ_{xy} \partial u \partial xx + τ_{xy} \partial u \partial yy + σ_{yy} \partial v \partial xx + \\ \partial v \partial xx - Wy) \partial q \partial y] \det (J^{e}) \end{array}$ (19)

其中, $\det (J^{e})$ 表示当前单元雅克比矩阵的行列式. 利用高斯积分法,对高斯点上的函数值求和就能计算出经过积分路径的一个单元的M 积分,其近似计算为

$M^{e} \approx I (r_{1}, s_{1}) + I (r_{2}, s_{2}) + I (r_{3}, s_{3}) + I (r_{4}, s_{4})$ (20)

如此重复计算积分路径穿过的所有单元,如图2所示,就可以得到对应于某个积分路径下的M 积分值.

显示原图| 下载原图ZIP| 生成PPT

图2 域积分法计算M 积分

Fig. 2 Domain integral method of calculating the M integral

同样的,三维M 积分的计算从定义式(14)出发,在使用有限元方法得到位移矩阵之后,通过物理、几何方程以及应力磨平等方法,可以进一步得到三维应力场、应变场等主要变量. 因此对于三维M 积分来说,求解的核心就是位移偏导数 $u_{j, i}$ 的计算. 为此,我们将其处理为

$\frac{\partial u_{j}}{\partial x_{i}} = \frac{Δ u_{j}}{Δ x_{i}}$ (21)

进行位移场的梯度计算,近似等于位移偏导数. 在计算M 积分时,为了保证其路径无关性,需在弹性区域选取包围所有缺陷的闭合曲面 $S$ 作为积分路径(球面等),将积分项中所需的值全部映射到曲面 $S$ 上进行积分,得到当前构型下三维M 积分值 ^[32].

2 基于M积分的缺陷材料等效损伤面积/体积标定方法

2.1 损伤标定方法阐述

基于以上现状分析和M 积分明确物理意义,我们基于M 积分提出一种缺陷损伤面积/体积标定方法. 此方法的适用范围广泛,研究表明若积分路径为包含所有微缺陷的闭合曲线时,作为材料构型力重要概念之一的M 积分,其值取决于材料属性、载荷条件以及缺陷构型(形状、尺寸、分布)等影响损伤水平的因素. 不受材料类型、缺陷构型限制. 只要能够计算出M 积分就能通过该方法等效出具有相同M 积分值的圆孔(球孔)的面积(体积). 此方法不止局限于具有解析解的M 积分缺陷,也能够通过数值计算出复杂缺陷构型情况的M 积分值进行损伤等效. 然而,对于三维情况,材料内缺陷构型不明(透明材料除外,玻璃、PMMA等),相应的数值模拟及M 积分计算无法实现. 因此,本方法的适用性局限于此,需要结合材料内缺陷的无损检测技术共同研究.

通过M 积分等效方法,对于不同类型缺陷致损伤水平,通过计算其导致的M 积分值来量化. 如图3(a)所示,二维情况下,相同的M 积分值代表着相同的损伤水^{[28,29,30,31,32,33]},则复杂缺陷致损伤面积标定为具有相同M 积分值的等效圆孔面积,实现原始缺陷的损伤面积标定,从而判断缺陷损伤水平. 其中二维圆孔的受远场载荷作用的M 积分值具有解析解 ^[9],记为 $M_{2 D - void}$ . 同样的,三维情况下,通过等效M 积分方法,复杂体内缺陷致损伤体积标定为具有相同M 积分值的等效球孔体积,其中球孔受远场载荷作用的M 积分值具有解析解 ^[34],记为 $M_{3 D - void}$ . 本研究针对材料复杂微缺陷构型的等效损伤面积/体积标定研究,具体方法如下：

(1) 有限元数值模拟损伤水平待评定的含复杂缺陷构型二维或三维弹性体(如图3所示),取围绕所有缺陷的积分路径,基于域积分法计算其M 积分值(统一记为 $M_{D}$ );

(2) 对于二维板,将上述计算得出的 $M_{D}$ ,代入缺陷的等效损伤面积表达式 $A_{D} = π R^{2} M_{D} / M_{2 D - void}$ ,以此计算出的 $A_{D}$ 作为各类二维缺陷构型的等效损伤面积;

(3) 对于三维体,将步骤(1)计算的 $M_{D}$ ,代入缺陷的等效损伤体积表达式 $V_{D} = 4 π R^{3} M_{D} /$ $(3 M_{3 D - void})$ ,以此计算出的 $V_{D}$ 作为各类三维缺陷的等效损伤体积.

显示原图| 下载原图ZIP| 生成PPT

图3 (a)二维缺陷等效损伤面积示意图;(b)三维缺陷等效损伤体积示意图

Fig. 3 Schematic diagram of calibrating the (a) equivalent damage area for two-dimensional multi-defects, and (b) equivalent damage volume for three-dimensional multi-defects

2.2 二维线弹性材料缺陷等效损伤面积标定算例

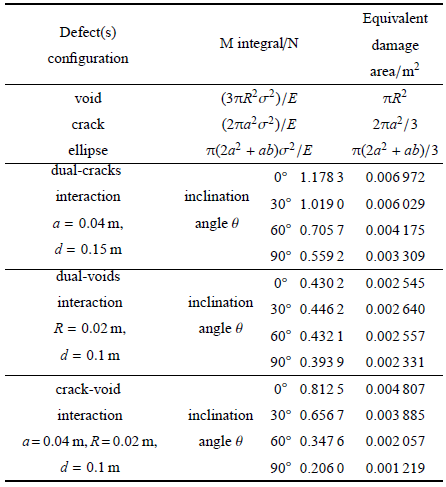
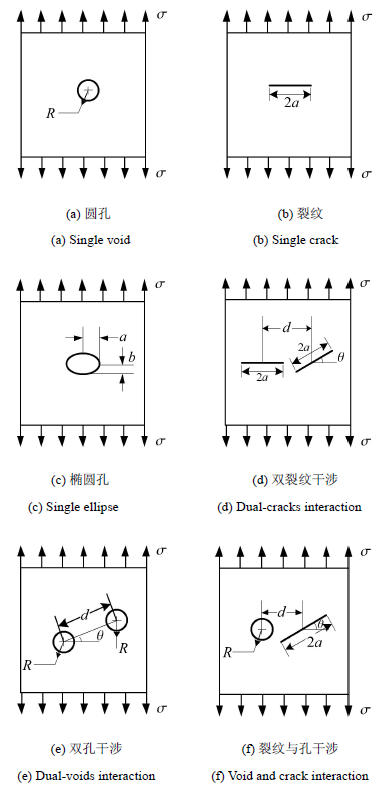
对于具有M 积分解析解的缺陷 ^[9](如单个裂纹、圆孔、椭圆孔等),通过等效M 积分的材料损伤面积标定方法能够直接确定其等效损伤面积. 而对于没有M 积分的解析解的缺陷,通过有限元计算缺陷导致的M 积分值来间接预测等效损伤面积. 对于图4所示的含缺陷二维板受到远场单轴拉伸载荷作用,板中含有各类缺陷构型,如裂纹、孔洞及相互间的干涉等, 其中板尺寸足够大,边界效应可以忽略. 本研究数值案例弹性模量为 $E = 71$ GPa,泊松比 $v = 0.33$ .

显示原图| 下载原图ZIP| 生成PPT

图4 二维弹性材料等效损伤面积标定实施算例示意图

Fig. 4 Equivalent damage area calculation for representative defect configurations within two-dimensional elastic plane

由表1可以看出,裂纹的真实损伤面积并不是其直观几何面积,而是基于M 积分的等效材料损伤面积 $2 π a^{2} / 3$ ; 同样椭圆孔的等效损伤面积为 $π (2 a^{2} + ab) / 3$ . 当椭圆孔与圆孔几何面积相等时(即 $R^{2} = ab$ ,其中 $R$ 为圆孔半径、 $a$ 为椭圆长半轴、 $b$ 为短半轴),圆孔的等效损伤面积为 $π R^{2} = π ab$ ,而椭圆孔的等效损伤面积为 $π (2 a^{2} + ab) / 3$ ,很明显 $π (2 a^{2} + ab) / 3 \geq π ab$ 恒成立,即几何面积相同的圆孔缺陷和椭圆孔缺陷对材料造成的损伤水平不一样,其中椭圆孔缺陷损伤面积大于圆孔损伤面积.

表1 二维弹性材料不同缺陷等效损伤面积标定结果

Table 1 The calculated results of equivalent damage area for various defect(s) configurations within two-dimensional elastic plane

新窗口打开

此外,缺陷相互干涉对材料的损伤水平影响也得到了体现. 缺陷构型为双裂纹干涉情况下,两条裂纹中心距离 $d$ 给定时,两条裂纹均垂直于载荷方向时,等效损伤面积最大,代表此时对材料的损伤水平最高. 在倾斜角 $θ$ 等于0 °时,理论上如果两裂纹相距足够远时,等效损伤面积 $A_{D}^{0^{\circ}} = 4 π a^{2} / 3 = 0.006 702$ m²,而本研究取两裂纹中心相距 $d = 0.15$ m时,数值计算等效损伤面积为 $0.006 972 = 104.03 % A_{D}^{0^{\circ}}$ ,表明由于两裂尖应力场的干涉,产生“反屏蔽效应”,导致等效损伤面积增大,即,提高材料的真实损伤水平, 促进缺陷进一步演化,与文献研究结果一致^[3,4]. 在倾斜角 $θ$ 等于90 °时,理论上如果两裂纹相距足够远时,等效损伤面积 $A_{D}^{9 0^{\circ}} = 2 π a^{2} / 3 = 0.003 351$ m²,而相距 $d = 0.15$ m时,数值计算等效损伤面积为0.003 309 m²=98.75% $A_{D}^{9 0^{\circ}}$ ,表明平行于拉伸载荷方向的裂纹对垂直于拉伸载荷方向的裂纹具有“屏蔽效应”,阻碍该裂纹扩展. 对比发现,缺陷之间距离越近,这种干涉效应越明显. 在缺陷构型为双孔干涉时,等效损伤面积随着两孔中心连线与水平轴之间的夹角增大而先增大再减小,表明多孔洞致材料损伤水平与孔洞间的相对分布位置有关. 以现有数据来看,倾斜角 $θ$ = 30°时,等效损伤面积最大;倾斜角 $θ$ = 90°时,等效损伤面积最小,但总体变化不明显. $θ$ = 0 °时,如果孔洞间距 $d$ 足够大,双孔等效损伤面积 $A_{D}$ 等于2倍的单孔情况下的损伤面积,即 $A_{D} = 2 π R^{2} = 0.002 513$ m²,而本研究取两孔洞中心相距 $d = 0.1$ m时,数值计算等效损伤面积为0.002 545 m² = 101.27% $A_{D}$ ,表明相对于双孔干涉情况,孔洞之间的干涉效应对材料损伤水平影响不大. 缺陷构型为裂纹与圆孔干涉情况下,裂纹中心与孔中心距离 $d$ 给定时,裂纹中心与孔中心连线垂直于载荷方向时,等效损伤面积最大,材料的损伤水平最高. 相对倾斜角 $θ$ = 0 °时,理论上如果裂纹和孔相距足够远时,等效损伤面积 $A_{D}^{0^{\circ}} = 2 π a^{2} / 3 + π R^{2} = 0.004 608$ m²,而本研究取裂纹和孔中心相距 $d = 0.1$ m,相对倾斜角 $θ$ = 0 °时,数值计算等效损伤面积为0.004 807 m² = 104.32% $A_{D}^{0^{\circ}}$ ,表明孔和裂纹的干涉效应导致损伤水平提高,由于孔洞的存在,裂纹启裂、扩展导致材料失效更容易发生. 相对倾斜角 $θ$ = 90 °,距离 $d$ 足够大时,理论等效损伤面积 $A_{D}^{9 0^{\circ}} = π R^{2} = 0.001 257$ m²,而本研究取裂纹和孔中心相距 $d = 0.1$ m时,数值计算等效损伤面积为0.001 219 m²= 97% $A_{D}^{9 0^{\circ}}$ ,表明裂纹平行于载荷方向时,孔和裂纹的干涉效应导致损伤水平降低,裂纹的存在导致孔洞启裂更难发生.

2.3 材料三维缺陷等效损伤体积标定算例

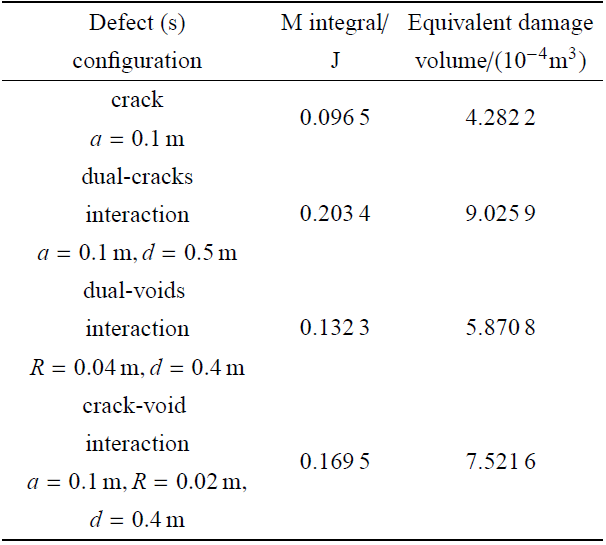
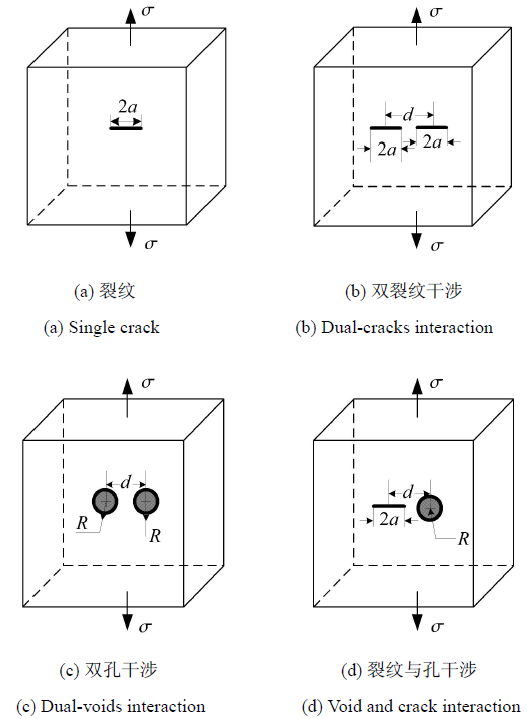
对于三维问题,单轴拉伸载荷作用下的弹性球孔缺陷的M 积分解析解 ^[34]为 $M_{3 D - void} = 16 π R^{3} σ^{2} / (3 E)$ . 由此可以用来标定各类缺陷等效损伤体积. 三维实例同二维实例一样,选取材料弹性模量 $E = 71$ GPa,泊松比 $v = 0.33$ . 通过有限元数值模拟含复杂缺陷构型的三维弹性体,其中含有不同缺陷构型,如图5所示.

通过表2可以看出,对于三维线弹性材料存在内部复杂缺陷的情况,通过M 积分的材料等效损伤体积标定方法,将内部存在的各类不同缺陷形貌损伤体积等效为一个球孔的体积,基于等效损伤体积评估各种缺陷形貌导致的材料损伤水平. 本研究的三维数值计算过程中,缺陷构型为双裂纹干涉情况时, 如果两裂纹相距足够远时,等效损伤体积 $V_{D}$ 等于两倍的单裂纹情况下的等效损伤体积, 即 $V_{D} = 0.000 856 4$ m³,而本研究取两裂纹中心相距 $d = 0.5$ m时,数值计算等效损伤面积为0.000 902 5 m³=105.38% $V_{D}$ ,表明由于两裂尖应力场的干涉,产生“反屏蔽效应”,导致等效损伤面积增大,即,提高材料的真实损伤水平,促进缺陷进一步演化. 在缺陷构型为双孔干涉时,如果两孔洞相距足够远时,等效损伤体积 $V_{D}$ 等于两倍的单孔洞情况下的等效损伤体积,即 $V_{D} = 8 π R^{3} / 3 = 0.000 536 2$ m³. 而本研究取两孔洞中心相距 $d = 0.4$ m时,数值计算等效损伤面积为0.000 587 1 m³=109.5% $V_{D}$ ,表明三维情况下,双孔洞之间的干涉效应导致材料损伤水平增大. 缺陷构型为裂纹与球孔干涉情况时,理论上如果裂纹和孔相距足够远时,等效损伤体积为单孔及单裂纹致材料损伤的叠加, $V_{D}$ =4 $π a^{3}$ /3+0.000 428 2=0.000 696 2 m³,而本研究取裂纹与孔洞中心相距 $d = 0.4$ m时,数值计算等效损伤面积为0.000 752 2 m³=108.04% $V_{D}$ ,表明三维情况下,孔和裂纹的干涉效应导致损伤水平提高,由于孔洞的存在,裂纹启裂、扩展导致材料失效更容易发生.

显示原图| 下载原图ZIP| 生成PPT

图5 三维缺陷材料等效损伤体积标定计算实施

Fig. 5 Equivalent damage volume calculation for representative defect configurations within three-dimensional elastic body

表2 针对不同三维缺陷的等效损伤体积

Table 2 The calculated results of equivalent damage volume for various defect(s) configurations within three-dimensional elastic body

新窗口打开

3 结论

本研究针对含复杂微缺陷的脆性材料损伤水平标定研究,提出了基于M 积分的等效损伤面积/体积标定方法,可以得出如下主要结论：

(1) 基于M积分代表着材料缺陷自相似扩展的能量释放率,本文提出材料的损伤水平以具有相同M 积分值的圆孔面积或球孔体积来标定. 基于M 积分的材料等效损伤面积/体积标定方法,可适用于材料含复杂微缺陷构型的情况;

(2) 脆性材料中,相同面积的圆孔和椭圆孔造成的等效损伤面积不一样. 单裂纹的等效损伤面积不是直观的0 (二维单轴拉伸情况下等于 $2 π a^{2} / 3$ ). 双裂纹干涉效应受裂纹相对倾斜角影响,单轴拉伸情况下,其中一条裂纹垂直于载荷方向时,双裂纹相对倾斜角 $θ$ 为0 °的情况下,由于两裂尖应力场的干涉产生“反屏蔽”效应;而相对倾斜角为90 °的情况下,由于其中一条裂纹平行于载荷方向产生“屏蔽”效应;

(3) 双孔洞干涉时,损伤水平随着两孔相互倾斜角 $θ$ 先增大再减小,表明多孔缺陷致材料损伤与孔洞间的相对分布位置有关;裂纹和孔洞的干涉效应主要与裂纹和孔洞的相对倾斜角度 $θ$ 相关联,而总体损伤水平主要取决于裂纹与拉伸载荷的夹角;

(4) 本方法计算方便,损伤表征更符合材料复杂缺陷的实际情况,具有明确的物理意义,可实现缺陷等级划分标准的统一性、普适性,将有益于材料及结构的剩余强度设计及完整性评估.

The authors have declared that no competing interests exist.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]	Shao JF, Rudnicki JW. A microcrack-based continuous damage model for brittle geomaterials . Mechanics of Materials, 2000, 177-180(10): 607-619 [本文引用: 1]
[2]	嵇醒. 断裂力学判据的评述 . 力学学报, 2016, 48(4): 741-753 [本文引用: 1] (Ji Xing. A critical review on criteria of fracture mechanics .Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(4): 741-753 (in Chinese)) [本文引用: 1]
[3]	Chen YH. M-integral analysis for two-dimensional solids with strongly interacting microcracks. Part 1: In an infinite brittle solid .International Journal of Solids and Structures, 2001, 38(18): 3193-3212 [本文引用: 3]
[4]	Chen YH. M-integral analysis for two-dimensional solids with strongly interacting microcracks. Part 2: In the brittle phase of an infinite metal/ceramic bimaterial .International Journal of Solids and Structures, 2001, 38(18): 3213-3232 [本文引用: 3]
[5]	Ju JW, Chen TM. Effective elastic moduli of two-dimensional brittle solids with interacting microcracks, part II: Evolutionary damage models .Journal of Applied Mechanics, 1994, 61(2): 358-366 [本文引用: 1]
[6]	Hu Y, Chen Y. The M -integral description for a brittle plane strip with two holes before and after coalescence .Acta Mechanica, 2009, 204(1-2):109-123 [本文引用: 2]
[7]	Yu MH. Advances in strength theories for materials under complex stress state in the 20th Century .Advances in Mechanics, 2004, 34(4): 529-560 [本文引用: 1]
[8]	GB/T1979 -2001 . 结构钢低倍组织缺陷评级图 [本文引用: 1] (GB/T1979 -2001 . Standard diagrams for macrostructure and defect of structural steels (in Chinese)) [本文引用: 1]
[9]	Pak YE, Mishra D, Yoo SH. Energy release rates for various defects under different loading conditions . Journal of Mechanical Science and Technology, 2012, 26(11): 3549-3554 [本文引用: 3]
[10]	徐真军, 杨红兵. 关于条形缺陷的射线照相评级探讨 .无损探伤, 2010, 34(2): 28-29 [本文引用: 1] (Xu Zhenjun, Yang Honbing. Analysis of the strip defect rating by using the radiography technology .Nondestructive Testing, 2010, 34(2): 28-29 (in Chinese)) [本文引用: 1]
[11]	汪孝欢, 牛显明, 张鹏林等. 焊缝数字图像圆形缺陷的自动评级方法 . 无损检测, 2012, 34(9): 42-45 [本文引用: 1] (Wang Xiaohuan, Niu Xianming, Zhang Penglin, et al. Research on automatic rating method for digital image circular weld defects .Nondestructive Testing, 2012, 34(9): 42-45 (in Chinese)) [本文引用: 1]
[12]	Eshelby JD, Frank FC, Nabarro FRN. XLI. The equilibrium of linear arrays of dislocations .Philosophical Magazine, 1951, 42(327): 351-364 [本文引用: 1]
[13]	Baxevanakis KP, Giannakopoulos AE. Finite element analysis of discrete edge dislocations: Configurational forces and conserved integrals .International Journal of Solids & Structures, 2015, 62: 52-65 [本文引用: 1]
[14]	Judt PO, Ricoeur A. A new application of M- and L-integrals for the numerical loading analysis of two interacting cracks .Journal of Applied Mathematics and Mechanics, 2015, 96(1): 24-36 [本文引用: 1]
[15]	Özenç K, Chinaryan G, Kaliske M. A configurational force approach to model the branching phenomenon in dynamic brittle fracture .Engineering Fracture Mechanics, 2016, 157: 26-42 [本文引用: 1]
[16]	古斌, 郭宇立, 李群. 基于构型力断裂准则的裂纹与夹杂干涉问题 . 力学学报, 2017, 49(6): 1312-1321 [本文引用: 1] (Gu Bin, Guo Yuli, Li Qun. Crack interacting with an individual inclusion by the fracture criterion of configurational force .Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(6): 1312-1321 (in Chinese)) [本文引用: 1]
[17]	Guo YL, Li Q. Material configurational forces applied to mixed mode crack propagation .Theoretical and Applied Fracture Mechanics, 2017, 89: 145-157 [本文引用: 1]
[18]	Tracy J, Waas A, Daly S. Experimental assessment of toughness in ceramic matrix composites using the J -integral with digital image correlation part I: Methodology and validation .Journal of Materials Science, 2015, 50(13): 4646-4658 [本文引用: 1]
[19]	Paxevanakis BK, Giannakopoulos AE. Finite element analysis of discrete edge dislocations: Configurational forces and conserved integrals .International Journal of Solids and Structures, 2015, 62(52-65): 52-65 [本文引用: 1]
[20]	李群. 材料构型力学及其在复杂缺陷系统中的应用 . 力学学报, 2015, 47(2): 197-214 [本文引用: 1] (Li Qun. Material configurational mechanics with application to complex defects .Acta Mechanica Sinica, 2015, 47(2): 197-214 (in Chinese)) [本文引用: 1]
[21]	Hu YF, Chen YH. The M-integral description for a brittle plane strip with two cracks before and after coalescence .Journal of Applied Mechanics, 2009, 76(6): 061017 [本文引用: 1]
[22]	于宁宇, 李群. M积分与夹杂/缺陷弹性模量的显式关系 . 力学学报, 2014, 46(1): 87-93 [本文引用: 1] (Yu Ningyu, Li Qun. The explicit relation between the m-integral and the elastic moduli of inclusion/damages .Acta Mechanica Sinica, 2014, 46(1): 87-93 (in Chinese)) [本文引用: 1]
[23]	Yu NY, Li Q. Failure theory via the concept of material configurational forces associated with the M-integral .International Journal of Solids & Structures, 2013, 50(25-26): 4320-4332 [本文引用: 1]
[24]	Li Q, Guo YL, Hou JL, et al. The M- integral based failure description on elasto-plastic materials with defects under biaxial loading .Mechanics of Materials, 2017, 112: 163-171 [本文引用: 1]
[25]	Goldstein RV, Shifrin EI, Shushpannikov PS. Application of invariant integrals to the problems of defect identification .International Journal of Fracture, 2007, 147(1-4): 45-54 [本文引用: 1]
[26]	Gommerstadt BY. The J and M integrals for a cylindrical cavity in a time-harmonic wave field .International Journal of Engineering Science, 2014, 83: 76-84 [本文引用: 1]
[27]	Meyer CR, Hutchinson JW, Rice JR. The path-independent M integral implies the creep closure of englacial and subglacial channels. Journal of Applied Mechanics, 2016, 84(1):011006(1-9) [本文引用: 1]
[28]	Ma LF, Chen YH, Liu CS. On the relation between the M-integral and the change of the total potential energy in damaged brittle solids .Acta mechanica, 2001, 150(1): 79-85 [本文引用: 2]
[29]	Li FZ, Shih CF, Needleman A. A comparison of methods for calculating energy release rates .Engineering Fracture Mechanics, 1985, 21(2): 405-421 [本文引用: 3]
[30]	Moran B, Shih CF. A general treatment of crack tip contour integrals .International Journal of Fracture, 1987, 35(4): 295-310 [本文引用: 3]
[31]	Nikishkov GP, Atluri SN. An equivalent domain integral method for computing crack-tip integral parameters in non-elastic, thermo-mechanical fracture .Engineering Fracture Mechanics, 1987, 26(6): 851-867 [本文引用: 3]
[32]	Shivakumar KN, Raju IS. An equivalent domain integral method for three-dimensional mixed-mode fracture problems .Engineering Fracture Mechanics, 1992, 42(6): 935-959 [本文引用: 2]
[33]	Chen YZ, Lee KY. Analysis of the M-integral in plane elasticity .Journal of Applied Mechanics, 2004, 71(4): 572-574 [本文引用: 1]
[34]	Seo SY, Mishra D, Park CY, et al. Energy release rates for a misfitted spherical inclusion under far-field mechanical and uniform thermal loads .European Journal of Mechanics, 2015, 49: 169-182 [本文引用: 2]

A microcrack-based continuous damage model for brittle geomaterials

2000

... 脆性材料(陶瓷、玻璃、混凝土、岩石等)广泛应用在机械、建筑等多个领域,其断裂失效常常起源于制造及服役过程中产生的缺陷 (裂纹、夹杂、孔洞等). 微缺陷的存在导致脆性结构服役过程中发生损伤演化. 针对脆性材料的多微缺陷致失效已经得到广泛研究^[1,2],其中涉及微裂纹扩展、微孔洞形核、聚合等^[3,4,5,6]. 微裂纹造成脆性材料不可逆的损伤,使得其强度、刚度等力学性能明显下降,进而会严重缩短材料的剩余使用寿命,对工程结构失效分析和强度校核带来了巨大挑战 ^[7]. 因此,对脆性材料中微缺陷进行统一的损伤水平标定,具有重要的科学研究和工程应用价值. ...

断裂力学判据的评述

2016

断裂力学判据的评述

2016

M-integral analysis for two-dimensional solids with strongly interacting microcracks. Part 1: In an infinite brittle solid

2001

... M 积分的物理意义可以理解为当前构型与无任何缺陷的构型之间,当各个缺陷表面的质点均以自相似的扩展方式达到当前构型时, 两种构型的总势能变化. 在线弹性材料情况下,计算缺陷的M 积分时,只需将积分路径完全包围缺陷便可以进行计算,且M 积分是一种路径无关积分,其值不依赖积分路径的选取^[3,4]. 另外,对于奇异应力场主导的各类缺陷问题,在远离缺陷的区域(不需要特别精密的网格),M 积分值可以通过域积分法准确求解^[29,30,31],将在后文作详细介绍. ...

... 此外,缺陷相互干涉对材料的损伤水平影响也得到了体现. 缺陷构型为双裂纹干涉情况下,两条裂纹中心距离

d

给定时,两条裂纹均垂直于载荷方向时,等效损伤面积最大,代表此时对材料的损伤水平最高. 在倾斜角

θ

等于0 °时,理论上如果两裂纹相距足够远时,等效损伤面积

A_{D}^{0^{\circ}} = 4 π a^{2} / 3 = 0.006 702

m²,而本研究取两裂纹中心相距

d = 0.15

m时,数值计算等效损伤面积为

0.006 972 = 104.03 % A_{D}^{0^{\circ}}

,表明由于两裂尖应力场的干涉,产生“反屏蔽效应”,导致等效损伤面积增大,即,提高材料的真实损伤水平, 促进缺陷进一步演化,与文献研究结果一致^[3,4]. 在倾斜角

θ

等于90 °时,理论上如果两裂纹相距足够远时,等效损伤面积

A_{D}^{9 0^{\circ}} = 2 π a^{2} / 3 = 0.003 351

m²,而相距

d = 0.15

m时,数值计算等效损伤面积为0.003 309 m²=98.75%

A_{D}^{9 0^{\circ}}

,表明平行于拉伸载荷方向的裂纹对垂直于拉伸载荷方向的裂纹具有“屏蔽效应”,阻碍该裂纹扩展. 对比发现,缺陷之间距离越近,这种干涉效应越明显. 在缺陷构型为双孔干涉时,等效损伤面积随着两孔中心连线与水平轴之间的夹角增大而先增大再减小,表明多孔洞致材料损伤水平与孔洞间的相对分布位置有关. 以现有数据来看,倾斜角

θ

= 30°时,等效损伤面积最大;倾斜角

θ

= 90°时,等效损伤面积最小,但总体变化不明显.

θ

= 0 °时,如果孔洞间距

d

足够大,双孔等效损伤面积

A_{D}

等于2倍的单孔情况下的损伤面积,即

A_{D} = 2 π R^{2} = 0.002 513

m²,而本研究取两孔洞中心相距

d = 0.1

m时,数值计算等效损伤面积为0.002 545 m² = 101.27%

A_{D}

,表明相对于双孔干涉情况,孔洞之间的干涉效应对材料损伤水平影响不大. 缺陷构型为裂纹与圆孔干涉情况下,裂纹中心与孔中心距离

d

给定时,裂纹中心与孔中心连线垂直于载荷方向时,等效损伤面积最大,材料的损伤水平最高. 相对倾斜角

θ

= 0 °时,理论上如果裂纹和孔相距足够远时,等效损伤面积

A_{D}^{0^{\circ}} = 2 π a^{2} / 3 + π R^{2} = 0.004 608

m²,而本研究取裂纹和孔中心相距

d = 0.1

m,相对倾斜角

θ

= 0 °时,数值计算等效损伤面积为0.004 807 m² = 104.32%

A_{D}^{0^{\circ}}

,表明孔和裂纹的干涉效应导致损伤水平提高,由于孔洞的存在,裂纹启裂、扩展导致材料失效更容易发生. 相对倾斜角

θ

= 90 °,距离

d

足够大时,理论等效损伤面积

A_{D}^{9 0^{\circ}} = π R^{2} = 0.001 257

m²,而本研究取裂纹和孔中心相距

d = 0.1

m时,数值计算等效损伤面积为0.001 219 m²= 97%

A_{D}^{9 0^{\circ}}

,表明裂纹平行于载荷方向时,孔和裂纹的干涉效应导致损伤水平降低,裂纹的存在导致孔洞启裂更难发生. ...

M-integral analysis for two-dimensional solids with strongly interacting microcracks. Part 2: In the brittle phase of an infinite metal/ceramic bimaterial

2001

... 此外,缺陷相互干涉对材料的损伤水平影响也得到了体现. 缺陷构型为双裂纹干涉情况下,两条裂纹中心距离

d

给定时,两条裂纹均垂直于载荷方向时,等效损伤面积最大,代表此时对材料的损伤水平最高. 在倾斜角

θ

等于0 °时,理论上如果两裂纹相距足够远时,等效损伤面积

A_{D}^{0^{\circ}} = 4 π a^{2} / 3 = 0.006 702

m²,而本研究取两裂纹中心相距

d = 0.15

m时,数值计算等效损伤面积为

0.006 972 = 104.03 % A_{D}^{0^{\circ}}

θ

等于90 °时,理论上如果两裂纹相距足够远时,等效损伤面积

A_{D}^{9 0^{\circ}} = 2 π a^{2} / 3 = 0.003 351

m²,而相距

d = 0.15

m时,数值计算等效损伤面积为0.003 309 m²=98.75%

A_{D}^{9 0^{\circ}}

θ

= 30°时,等效损伤面积最大;倾斜角

θ

= 90°时,等效损伤面积最小,但总体变化不明显.

θ

= 0 °时,如果孔洞间距

d

足够大,双孔等效损伤面积

A_{D}

等于2倍的单孔情况下的损伤面积,即

A_{D} = 2 π R^{2} = 0.002 513

m²,而本研究取两孔洞中心相距

d = 0.1

m时,数值计算等效损伤面积为0.002 545 m² = 101.27%

A_{D}

,表明相对于双孔干涉情况,孔洞之间的干涉效应对材料损伤水平影响不大. 缺陷构型为裂纹与圆孔干涉情况下,裂纹中心与孔中心距离

d

给定时,裂纹中心与孔中心连线垂直于载荷方向时,等效损伤面积最大,材料的损伤水平最高. 相对倾斜角

θ

= 0 °时,理论上如果裂纹和孔相距足够远时,等效损伤面积

A_{D}^{0^{\circ}} = 2 π a^{2} / 3 + π R^{2} = 0.004 608

m²,而本研究取裂纹和孔中心相距

d = 0.1

m,相对倾斜角

θ

= 0 °时,数值计算等效损伤面积为0.004 807 m² = 104.32%

A_{D}^{0^{\circ}}

,表明孔和裂纹的干涉效应导致损伤水平提高,由于孔洞的存在,裂纹启裂、扩展导致材料失效更容易发生. 相对倾斜角

θ

= 90 °,距离

d

足够大时,理论等效损伤面积

A_{D}^{9 0^{\circ}} = π R^{2} = 0.001 257

m²,而本研究取裂纹和孔中心相距

d = 0.1

m时,数值计算等效损伤面积为0.001 219 m²= 97%

A_{D}^{9 0^{\circ}}

,表明裂纹平行于载荷方向时,孔和裂纹的干涉效应导致损伤水平降低,裂纹的存在导致孔洞启裂更难发生. ...

Effective elastic moduli of two-dimensional brittle solids with interacting microcracks, part II: Evolutionary damage models

1994

The M -integral description for a brittle plane strip with two holes before and after coalescence

2009

... 当材料中的缺陷的构型(形状和位置)改变时,会引起材料自由能的变化. 与材料的构型变化相关的驱动力定义为构型力,又称“材料力”. 关于构型力的概念可以追溯到Eshelby等 ^[12]于1951年提出的能量动量张量概念,其物理意义可解释为单位厚度的无限小单元沿坐标轴平移所对应的势能变化量. 近年来,许多研究学者发现材料构型力学理论体系在描述含缺陷材料或构件的破坏行为方面具有得天独厚的优势^{[13,14,15,16,17,18,19,20]}. 其中,M积分作为材料构型力学理论体系的重要守恒积分,已广泛应用于断裂、损伤以及缺陷识别领域.^[6,21]基于有限元分析,系统研究了裂纹、孔洞缺陷在发生聚合前后,M积分的变化规律及其与材料有效弹性模量之间的内在联系,其认为M 积分值在缺陷聚合(干涉效应)时所发生的“跳跃”表明材料的损伤水平进一步加深. 另外,近年来,许多学者提出M 积分可以用来描述含复杂缺陷材料的破坏行为. 代表性的工作有,于宁宇等 ^[22] 的研究表明M积分不但可以表征材料构型上的不连续性,也能表征材料的非线性弹塑性行为. 远端载荷、材料行为以及缺陷构型对 M积分的影响表明M积分在描述材料的微缺陷损伤中具有重要作用. 随后又基于M 积分提出了新的统一失效准则 ^[23],该准则采用无量纲参数来表征材料的损伤水平,并假定当损伤累积到一个门槛值时, 材料发生失效. 随后,Li等 ^[24]基于数字图像相关技术,研究了含局部复杂缺陷的LY-12铝合金板(“十字形”试样)受双轴载荷作用下的失效行为,实验测得合金板的临界损伤参数,验证了该参数适用于含复杂缺陷、受复杂载荷作用的弹--塑性材料的失效评价. Goldstein等 ^[25]应用包括M 积分在内的守恒积分(J,M,L积分),结合简单的含球形孔/夹杂试件的单轴拉伸实验,对材料内部球形缺陷的半径、弹性模量及中心坐标进行了准确预测. Gommerstadt ^[26]应用M 积分以及J-积分,研究了含孔洞缺陷的固体受时域谐波激励作用发生振动失效的弹性动力学问题,并指出M 积分在无损检测中的潜在应用. 最近,Meyer 等 ^[27]应用M 积分研究了冰川下的排水通道的蠕变损伤闭合效应. 基于以上研究,M 积分的物理意义可以理解为当前构型与无任何缺陷构型之间,各个缺陷表面的质点均以自相似扩展方式达到当前构型时,两种构型的总势能变化,其代表着材料整体缺陷发生自相似扩展导致的能量释放率 ^[28],可应用于材料和结构的缺陷损伤标定. ...

Advances in strength theories for materials under complex stress state in the 20th Century

2004

-2001

1979

... 传统的缺陷标定大多基于直接观测法 ^[8],包括人工肉眼或使用放大镜观测缺陷,根据对缺陷进行分类,利用经验判断缺陷的损伤水平,或根据观测到的直观几何面积大小评定缺陷等级,但缺陷的直观几何面积与其造成的损伤水平(面积)并不直接呈正关系. 例如：裂纹类缺陷的几何面积近乎为零,这显然不匹配其实际造成的损伤水平;而几何面积相同的圆孔缺陷和椭圆孔缺陷对材料造成的损伤也有很大差别 ^[9]. 总体来说,缺陷对材料的损伤水平一般为裂纹大于椭圆孔,椭圆孔大于圆孔. 此外,对于复杂缺陷情况,缺陷数量巨大、尺寸不一、形态各异,使得人工分类、评估非常困难,而缺陷间的相互干涉效应也无法表征. 因此,传统的人工标定方法已经不能适应现代工业生产对缺陷检测分析和评估的要求. ...

-2001

1979

Energy release rates for various defects under different loading conditions

2012

... 通过M 积分等效方法,对于不同类型缺陷致损伤水平,通过计算其导致的M 积分值来量化. 如图3(a)所示,二维情况下,相同的M 积分值代表着相同的损伤水^{[28,29,30,31,32,33]},则复杂缺陷致损伤面积标定为具有相同M 积分值的等效圆孔面积,实现原始缺陷的损伤面积标定,从而判断缺陷损伤水平. 其中二维圆孔的受远场载荷作用的M 积分值具有解析解 ^[9],记为

M_{2 D - void}

. 同样的,三维情况下,通过等效M 积分方法,复杂体内缺陷致损伤体积标定为具有相同M 积分值的等效球孔体积,其中球孔受远场载荷作用的M 积分值具有解析解 ^[34],记为

M_{3 D - void}

. 本研究针对材料复杂微缺陷构型的等效损伤面积/体积标定研究,具体方法如下： ...

... 对于具有M 积分解析解的缺陷 ^[9](如单个裂纹、圆孔、椭圆孔等),通过等效M 积分的材料损伤面积标定方法能够直接确定其等效损伤面积. 而对于没有M 积分的解析解的缺陷,通过有限元计算缺陷导致的M 积分值来间接预测等效损伤面积. 对于图4所示的含缺陷二维板受到远场单轴拉伸载荷作用,板中含有各类缺陷构型,如裂纹、孔洞及相互间的干涉等, 其中板尺寸足够大,边界效应可以忽略. 本研究数值案例弹性模量为

E = 71

GPa,泊松比

v = 0.33

. ...

关于条形缺陷的射线照相评级探讨

2010

... 目前应用较多的缺陷质量分级办法中还包括无损检测标定方法,选择适宜的无损检测技术后,针对于不同类型的缺陷采用不同的质量分级办法. 徐真军等 ^[10]针对长宽比大于3的“条形缺陷”通过规定在待评定区长度和相邻缺陷距离内,任意一组“条形缺陷”的累计长度范围来划分等级,在不同类型缺陷评定质量级别不同时,以质量最差的级别作为其真实质量等级. 汪孝欢等 ^[11]针对长宽比不大于3的“圆形缺陷”,在缺陷最严重的区域根据母材尺寸选择相应的缺陷评定区,根据每个级别在各评定区尺寸所允许的圆形缺陷点数表格来划分质量等级. 实际工程中,存在很多不规则的缺陷,为了应用断裂力学分析缺陷,往往将它们处理成规范性裂纹,即半椭圆裂纹、椭圆埋藏裂纹、穿透裂纹,但这种简化过程不完全符合实际情况,很难保证其准确性. 总体来说,基于不同的缺陷检测方法以及针对不同类型缺陷使用的质量分级办法,各类缺陷对材料造成的损伤水平无法进行统一评估标定,且多数质量分级根据经验划分. 目前,尚缺乏一种适用于各类受检物、复杂缺陷的材料真实损伤面积标定方法. ...

关于条形缺陷的射线照相评级探讨

2010

焊缝数字图像圆形缺陷的自动评级方法

2012

焊缝数字图像圆形缺陷的自动评级方法

2012

XLI. The equilibrium of linear arrays of dislocations

1951

Finite element analysis of discrete edge dislocations: Configurational forces and conserved integrals

2015

A new application of M- and L-integrals for the numerical loading analysis of two interacting cracks

2015

A configurational force approach to model the branching phenomenon in dynamic brittle fracture

2016

基于构型力断裂准则的裂纹与夹杂干涉问题

2017

基于构型力断裂准则的裂纹与夹杂干涉问题

2017

Material configurational forces applied to mixed mode crack propagation

2017

Experimental assessment of toughness in ceramic matrix composites using the J -integral with digital image correlation part I: Methodology and validation

2015

Finite element analysis of discrete edge dislocations: Configurational forces and conserved integrals

2015

材料构型力学及其在复杂缺陷系统中的应用

2015

材料构型力学及其在复杂缺陷系统中的应用

2015

The M-integral description for a brittle plane strip with two cracks before and after coalescence

2009

M积分与夹杂/缺陷弹性模量的显式关系

2014

M积分与夹杂/缺陷弹性模量的显式关系

2014

Failure theory via the concept of material configurational forces associated with the M-integral

2013

The M- integral based failure description on elasto-plastic materials with defects under biaxial loading

2017

Application of invariant integrals to the problems of defect identification

2007

The J and M integrals for a cylindrical cavity in a time-harmonic wave field

2014

The path-independent M integral implies the creep closure of englacial and subglacial channels.

2016

On the relation between the M-integral and the change of the total potential energy in damaged brittle solids

2001

M_{2 D - void}

M_{3 D - void}

. 本研究针对材料复杂微缺陷构型的等效损伤面积/体积标定研究,具体方法如下： ...

A comparison of methods for calculating energy release rates

1985

... 引入弱函数

q

,具有恒等式(

M_{i} q)_{i} = M_{i, i} q + M_{i} q_{, i}

,M 积分的计算对于假设的函数

q

的形式并不敏感,因此函数

q

可以任意选取. 给定

q = x_{i}

,基于域积分法 ^[29,30,31]将M 积分转化为域积分后的形式为 ...

M_{2 D - void}

M_{3 D - void}

. 本研究针对材料复杂微缺陷构型的等效损伤面积/体积标定研究,具体方法如下： ...

A general treatment of crack tip contour integrals

1987

... 引入弱函数

q

,具有恒等式(

M_{i} q)_{i} = M_{i, i} q + M_{i} q_{, i}

,M 积分的计算对于假设的函数

q

的形式并不敏感,因此函数

q

可以任意选取. 给定

q = x_{i}

,基于域积分法 ^[29,30,31]将M 积分转化为域积分后的形式为 ...

M_{2 D - void}

M_{3 D - void}

. 本研究针对材料复杂微缺陷构型的等效损伤面积/体积标定研究,具体方法如下： ...

An equivalent domain integral method for computing crack-tip integral parameters in non-elastic, thermo-mechanical fracture

1987

... 引入弱函数

q

,具有恒等式(

M_{i} q)_{i} = M_{i, i} q + M_{i} q_{, i}

,M 积分的计算对于假设的函数

q

的形式并不敏感,因此函数

q

可以任意选取. 给定

q = x_{i}

,基于域积分法 ^[29,30,31]将M 积分转化为域积分后的形式为 ...

M_{2 D - void}

M_{3 D - void}

. 本研究针对材料复杂微缺陷构型的等效损伤面积/体积标定研究,具体方法如下： ...

An equivalent domain integral method for three-dimensional mixed-mode fracture problems

1992

... 进行位移场的梯度计算,近似等于位移偏导数. 在计算M 积分时,为了保证其路径无关性,需在弹性区域选取包围所有缺陷的闭合曲面

S

作为积分路径(球面等),将积分项中所需的值全部映射到曲面

S

上进行积分,得到当前构型下三维M 积分值 ^[32]. ...

M_{2 D - void}

M_{3 D - void}

. 本研究针对材料复杂微缺陷构型的等效损伤面积/体积标定研究,具体方法如下： ...

Analysis of the M-integral in plane elasticity

2004

M_{2 D - void}

M_{3 D - void}

. 本研究针对材料复杂微缺陷构型的等效损伤面积/体积标定研究,具体方法如下： ...

Energy release rates for a misfitted spherical inclusion under far-field mechanical and uniform thermal loads

2015

M_{2 D - void}

M_{3 D - void}

. 本研究针对材料复杂微缺陷构型的等效损伤面积/体积标定研究,具体方法如下： ...

... 对于三维问题,单轴拉伸载荷作用下的弹性球孔缺陷的M 积分解析解 ^[34]为

M_{3 D - void} = 16 π R^{3} σ^{2} / (3 E)

. 由此可以用来标定各类缺陷等效损伤体积. 三维实例同二维实例一样,选取材料弹性模量

E = 71

GPa,泊松比

v = 0.33

. 通过有限元数值模拟含复杂缺陷构型的三维弹性体,其中含有不同缺陷构型,如图5所示. ...

〈

〉

基于M积分的脆性材料微缺陷等效损伤面积/体积表征

THE CALIBRATION OF MICRODEFECTS INDUCED EQUIVALENT DAMAGE AREA/VOLUME OF BRITTLE MATERIALS BY USING THE M-INTEGRAL

引言

1 M 积分的定义及其数值计算

1.1 M 积分定义

1.2 基于域积分法的 M 积分数值计算

2 基于M积分的缺陷材料等效损伤面积/体积标定方法

2.1 损伤标定方法阐述

2.2 二维线弹性材料缺陷等效损伤面积标定 算例

2.3 材料三维缺陷等效损伤体积标定算例

3 结 论

参考文献 文献选项 原文顺序 文献年度倒序 文中引用次数倒序 被引期刊影响因子

2.2 二维线弹性材料缺陷等效损伤面积标定算例

3 结论

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子