引言
颗粒材料广泛的存在于自然界与实际工程应用中,如土体,土石混合体,地质体以及混凝土结构中. 在介观尺度,颗粒材料由大量不同形状、尺度的离散固体颗粒及空隙组成,为高度非均质、非连续介质. 颗粒材料非线性、耗散等力学行为与其离散介观结构随力学响应的演变过程有着直接的联系. 联接宏--介观力学行为模拟的多尺度计算分析方法,被用以研究颗粒材料的复杂力学行为.
在介观尺度上颗粒材料的每个离散颗粒具有独立的旋转自由度与平动自由度,在接触点处能同时传递力和力偶. 因而在多尺度分析 中,它在宏观尺度上模型化为Cosserat连续体,而不是Cauchy连续 体[1 ,2 ,3 ,4 ,5 ,6 ,7 ] . 非均质材料的介--宏观计算均匀化模拟基于Hill定理,据此可以给定表征元(representation volume element, RVE)的静力学或运动学容许边界条件,使得Hill-Mendal宏--介观能量等价条件得到满足[8 ,9 ] .
经典Cosserat连续体的Hill定理表明[4 ,9 ] ,宏观Cosserat连续体仅能下传与施加均一性宏观应变场于表征元边界. 作用于表征 元均一宏观应变场的合理性基于尺度分离概念,考虑到表征元尺寸并非远小于宏观连续体有限元分析的特征尺寸,特别是在高宏观应 变梯度(如应变局部化)区域尺度分离条件不再成立. 为施加非均一宏观应变场于表征元边界,要求在宏观尺度采用梯度增强Cosserat连续体模型 [10 ] ,并发展了相应的二阶计算均 匀化方法 [11 ] 和在宏--介观尺度的混合元--离散元嵌套算法 [12 ] .
然而,基于离散颗粒系统--连续体模型的颗粒材料计算多尺度方法的表征元介观尺度分析并不直接提供和上传表征相应积分点处损伤、 塑性等的内状态变量至宏观连续体,而这正是从事颗粒材料结构工程破坏分析的工程技术人员所关心和需要的数值模拟结果. 本文主要工作是在颗粒材料计算均匀化多尺度分析框架下,建议一个基于介观力学的宏观连续体中材料损伤--塑性表征 方法.
塑性的基本特征是连续体变形的不可恢复性以及在塑性变形过程中所做的塑性功的不可逆性. 经典连续损伤力学中材料损伤定义为 以弹性模量张量表示的弹性刚度降低[13 ,14 ,15 ] .
材料塑性与损伤描述了不可逆的能量耗散过程. 在连续介质力学唯象方法中,塑性与损伤理论研究基于热动力学框架与引入以唯象 形式定义的内变量以定量描述材料内部微结构演变和所伴随的不可逆能量耗散[16 ,17 ,18 ,19 ,20 ] .
损伤力学的近期研究表明,包括颗粒材料在内的许多工程材料在一定条件下具备愈合与部分恢复它们的刚度的潜 能[21 ,22 ,23 ,24 ,25 ] . 需要拓展经典连续损伤力学理论,以计及具有非耗散本质的愈合过程 [26 ] . 大部分模拟愈合过程的本构模型基于唯象理论 [26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ] . Ju等[31 ,32 ] 首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型.
需要指出的是,在损伤--塑性耦合分析的宏观唯象理论框架内,损伤现象一般假定为各向同性 [34 ] . 然而,对于包括颗粒 材料在内的具有非均质和复杂介观结构的材料,材料的损伤与愈合在本质上为各向异性. 各向异性来源于颗粒材料局部初始介观结构的各向异性以及由于颗粒材料力学响应导致的局部介观结构演变的各向异 性[35 ,36 ,37 ,38 ] .
本文从颗粒材料介观尺度的离散颗粒集合体力学响应分析出发,在二阶计算均匀化框架内对具有离散颗粒介观结构的表征元建立 了等价连续体的增量非线性本构方程;把连续体本构关系中所定义的塑性--损伤--愈合行为以离散颗 粒集合体中颗粒间相对耗散摩擦滑移、直接相邻颗粒间接触取向的改变、接触的丧失与再生等介观力学信息表示.
进一步,在颗粒材料热动力学框架 [38 ] 内定义了基于表征元介观力学信息的塑性应变以及各向异性损伤、愈合因子张量和 综合了各向异性损伤、愈合效应的净损伤因子张量. 进一步,以塑性、损伤耗散能与非耗散的愈合能等具有标量特征的内状态量表征并定量比较材料的塑性--损 伤--愈合效应. 应变局部化数值算例表明了基于介观力学信息的宏观梯度Cosserat连续体中塑性--损伤--愈合表征方 法的有效性.
1 凝聚于表征元边界的离散颗粒集合体非线 性增量本构方程
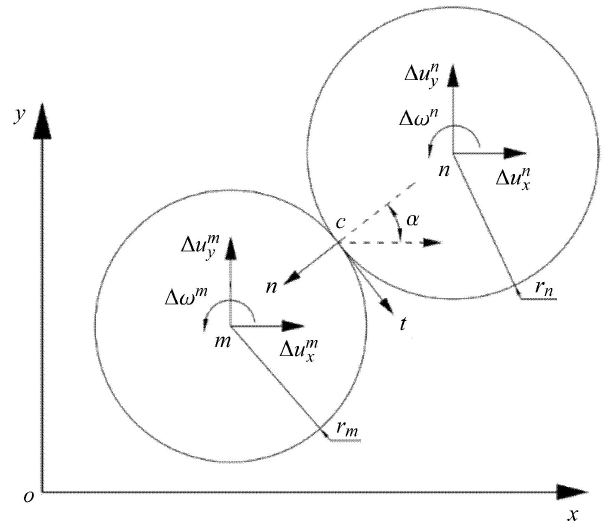
一对典型接触颗粒,在时间段 [ t i - 1 , t i ] m Δ u m = u x m u y m ω m T n Δ u n = u x n u y n ω n T 图1 所示.
图1 典型的接触颗粒对m n
Fig. 1 A typical contact between particle m n
颗粒 n m c n - t . 颗粒 n m
Δ u l nm = T nm Δ u nm (1)
其中
Δ u nm = Δ u n Δ u m T , T nm = T n T m
T n = cos α - sin α 0 sin α cos α r n 0 0 1 (2)
T m = - cos α - sin α 0 sin α - cos α r m 0 0 - 1 (3)
考虑颗粒接触间相对切向滑动和滚动以及相对转动对接触力的影响,颗粒 m n
Δ f l nm = K l T nm Δ u nm - Δ f l nm , p (4)
其中 Δ f l nm = Δ f n nm Δ f t nm Δ m nm T Δ f n nm Δ f t nm Δ m nm K l Δ f l nm , p = 0 Δ f t nm , p Δ m nm , p T
Δ f t nm , p = - k s nm Δ u s nm , p - k r nm Δ u r nm , p 2 mm ]
Δ m nm , p = k θ nm Δ θ r nm , p + k s nm Δ u s nm , p + k r nm Δ u r nm , p r n
Δ f t nm , p Δ m nm , p Δ u s nm , p Δ u s c Δ u r nm , p Δ u r c Δ θ r nm , p n , m Δ θ r c k s nm k r nm k θ nm
Δ f nm = T g K l T nm Δ u nm - Δ f l nm , p = K nm Δ u nm - Δ f nm , p (5)
其中 T g K nm = T g K l T nm Δ f nm , p = T g Δ f l nm , p
颗粒 n n
Δ f n = ∑ m=1 N m K nm Δ u nm - Δ f nm , p = ∑ m=1 N m K nm Δ u nm - ∑ m=1 N m Δ f nm , p (6)
其中 N m n
K II K IB K BI K BB Δ u I Δ u B - Δ F I p Δ F B p = Δ F I ext Δ F B ext (7)
其中 K II K IB K BI K BB Δ u I Δ u B Δ F I p Δ F B p Δ F I ext Δ F B ext Δ F I ext Δ F B ext
Δ u I = K II - 1 Δ F I p - K IB Δ u B
K B Δ u B - Δ F B p - K BI K II - 1 Δ F I p = Δ F B ext
其中 K B = K BB - K BI K II - 1 K IB Δ F B * = Δ F B p - K BI K II - 1 Δ F I p
K B Δ u B - Δ F B * = Δ F B ext (10)
其中 Δ F B ext Δ f B ext Δ m Bc ext Δ u B Δ u B Δ ω B Δ F B * Δ F u p Δ F ω * p
K uu b K u ω b K ω u b * K ωω b * Δ u B Δ ω B - Δ F u p Δ F * p = Δ f B ext Δ m Bc ext (11)
边界颗粒形心处力矩 Δ m Bc ext Δ f B ext Δ m B ext
Δ m Bc ext = Δ m B ext + R n T Δ f B ext (12)
其中 R n T
R n = R 1 c 0 0 0 ⋱ 0 0 0 R p c (13)
其中对于第 i R i c i = 1,2 , ⋯ , p
R i c = 0 r 3 c i - r 2 c i - r 3 c i 0 r 1 c i r 2 c i - r 1 c i 0 (14)
式中 r i c = x i c - x i x i x i c i
K uu b K u b K u b K ωω b Δ u B Δ ω B - Δ F u p Δ F p = Δ f B ext Δ m B ext (15)
式中 K u b = K u b * - R n T K uu b K b = K b * - R n T K u b Δ F p = Δ F * p - R n T Δ F u p Δ u B Δ u B c Δ u B = Δ u B c - R n Δ ω B
Δ f B ext = K uu b Δ u B c + K u bc Δ ω ̃ B - Δ F u p
Δ m B ext = K u b Δ u B c + K ωω bc Δ ω ̃ B - Δ F p
式中 K u bc = K u b - K uu b R n K bc = K b - K u b R n Δ f B ext Δ m B ext i i
Δ f i ext = ∑ j=1 N c K uu b ij Δ u B c j + K u bc ij Δ ω ̃ B j - ( Δ F u p ) i = ∑ j= 1 N c [ ( K uu b ) ij ( Δ u j c + ( K u bc ) ij Δ ω ̃ j ] - ( Δ F u p ) i (18)
其中, f , K , u , ω ̃
Δ m i ext = ∑ j=1 N c K u b ij Δ u B c j + K ωω bc ij Δ ω B j - ( Δ F p ) i =
∑ j=1 N c [ ( K wu b ) ij ( Δ u j c + ( K ωω bc ) ij Δ ω ̃ j ] - ( Δ F p ) i
其中 N c K uu b ij K u bc ij K u b ij K ωω bc ij K uu b K u bc K u b K ωω bc
2 基于介观力学信息的宏观梯度Cosserat连续体非线性增量本构关系
颗粒材料梯度增强Cosserat连续体中局部样条点(即有限元网格积分点)处的应力等于与该点相关联的表征元的平均应力. 它们可通过如下表征元的边界积分,边界积分可进一步离散到表征元中所有边界颗粒与表征元边界接触点处的力学与几何量,表示为
σ ̅ = 1 V ∫ S x ⊗ t dS = 1 V ∑ i=1 N c x i c ⊗ f i ext (20)
T ̅ = - e : σ = - 1 V e : ∑ i=1 N c x i c ⊗ f i ext (21)
Σ ̅ = 12 V ∫ S x ⊗ x ⊗ t dS = 12 V ∑ i=1 N c x i c ⊗ x i c ⊗ f i ext (22)
μ ̅ 0 = 1 V ∫ S x ⊗ m dS + 12 V ∫ S x ⊗ x ⊗ t dS : e = 1 V ∑ i=1 N c x i c ⊗ x i c ⊗ f i ext : e (23)
其中 σ ̅ T ̅ Σ ̅ μ ̅ 0 V S x t m e
根据Hill定理、满足Hill-Mandel能量条件而应施加于表征元边界离散颗粒处的边界条件为 [11 ]
Δ u B c i = x i c ⋅ Δ Γ ̅ + 12 ( x i c ⊗ x i c ) : Δ E ̅ ( 24 )
Δ ω ̅ B i = Δ ω ̅ + x i c ⋅ Δ κ ̅ ( 25 )
其中 Γ ̅ E ̅ ω ̅ κ ̅ σ ̅ Σ ̅ T ̅ μ ̅ 0
利用式(18)和式(19)以及式(24)和式(25),式(20) ~
Δ σ ̅ = D σ Γ : Δ Γ ̅ + D σ E ̂ ⋮ Δ E ̅ + D σ ω ⋅ Δ ω ̅ + D σ κ : Δ κ ̅ - Δ σ ̅ p Δ Σ = D Σ ̂ Γ : Δ Γ ̅ + D Σ ̂ E ̂ ⋮ Δ E ̅ + D Σ ̂ ω ⋅ Δ ω ̅ + D Σ ̂ κ : Δ κ - Δ Σ p Δ T ̅ = D T Γ : Δ Γ ̅ + D T E ̂ ⋮ Δ E ̅ + D σ T ⋅ Δ ω ̅ + D T κ : Δ κ - Δ T p Δ μ ̅ 0 = D μ Γ : Δ Γ ̅ + D μ E ̂ ⋮ Δ E ̅ + D μ ω ⋅ Δ ω ̅ + D μ κ : Δ κ - Δ μ 0 , p (26)
令
Δ Ξ ̅ = [ Δ σ ̅ Δ Σ ̅ Δ T ̅ Δ μ ̅ 0 ] T Δ Λ ̅ = [ Δ Γ ̅ Δ E ̅ Δ ω ̅ Δ κ ̅ ] T
式(26)可以写成
Δ Ξ ̅ = D t e ( Δ Λ ̅ - Δ Λ ̅ p ) = D t e Δ Λ ̅ - Δ Ξ ̅ p (27)
D t e = D σ Γ D σ E ̂ D σ ω D σ κ D Σ ̂ Γ D Σ ̂ E ̂ D Σ ̂ ω D Σ ̂ κ D T Γ D T E ̂ D T ω D T κ D μ Γ D μ E ̂ D μ ω D μ κ (28)
其中 D t e [11 ] 的弹性模量张量, Δ Λ ̅ p Δ Ξ ̅ p
Δ Ξ ̅ p = Δ σ ̅ p Δ Σ ̅ p Δ T ̅ p Δ μ ̅ 0 , p = 1 V ∑ i=1 N c x i c ⊗ ( Δ F u p ) i 1 2 V ∑ i=1 N c x i c ⊗ x i c ⊗ ( Δ F u p ) i - 1 V e : ∑ i=1 N c x i c ⊗ ( Δ F u p ) i 1 V ∑ i=1 N c x i c ⊗ ( Δ F ω p ) i + 1 2 V ∑ i=1 N c x i c ⊗ x i c ⊗ ( Δ F u p ) i : e (29)
式(27)为根据平均场理论与多尺度力学理论中Hill定理所导出的基于表征元介观结构与力学信息的联系宏观梯度Cosserat连续体局部材料点应力、应变、模量张量及塑性应变等物理量的非线性增量本构方程. 它是下节中基于表征元介观信息的宏观连续体塑性及净损伤表征的出发点.
3 基于介观结构的损伤--愈合因子张量与损伤--愈合--塑性过程的热动力学耗散能
文献[35,38]推导了基于颗粒材料离散介观信息的等价经典Cosserat连续体Voronoi胞元的非线性弹性本构关系,在热动力学框架下定义了损伤--愈合因子张量,给出了损伤--愈合和塑性的耗散能量密度的表达形式. 在此基础上,本文在颗粒材料二阶计算均匀化框架下,上节导出了梯度增强Cosserat连续体非线性弹性本构关系.
在连续损伤力学框架内,损伤--愈合因子张量 d
d = d D t e , D 0 e = I - D 0 e ⋅ D t e - 1 (30)
其中 I D 0 e D t e t i t i - 1 , t i
Δ d = - Δ D t e ⋅ D 0 e - 1 = - D t e i - D t e i - 1 ⋅ D 0 e - 1 (31)
热力学框架下,与损伤--愈合因子张量增量 Δ d [35 ]
Ξ d = 1 2 Σ i D t e - T ⋅ D 0 ⋅ D t e - 1 ij ⋅ δ jb δ ak Σ k e a ⊗ e b (32)
弹性损伤--愈合能密度增量为
Φ ̃ d = Ξ d : Δ d (33)
由于颗粒材料一般 为各向异性材料,其损伤--愈合效应也一般 为各向异性,甚至在一个方向损伤,而在另一个方向可能呈现材料愈合. 区分梯度增强Cosserat连续体中局部材料点处的损伤或愈合行为的准则为 Φ ̃ d = 0 Φ ̃ d > 0 Φ ̃ d < 0
根据式(27),宏观塑性应变增量可以表示为 Δ Λ p = ( D i e ) - 1 ⋅ Δ Ξ p (34) 塑性耗散能密度增量可表示为
Φ ̃ p = Ξ ̅ ⋅ Δ Λ ̅ p ≥ 0 (35)
4 数值算例
平板压缩算例,如图2 (a)所示. 忽略重力效应,因为满足对称性条件,数值模拟仅对1/4平板进行,如图2 (b)所示,其中 L = 30 20 × 20 图1 (b)所示.
图2 方板压缩问题
Fig. 2 Compression problem of a square panel
有限元网格中,每一个积分点处配置一个初始构形相同的表征元. 3种具有相同规则介观结构,但具有不同尺寸的表征元, 分别命名为RVE40, RVE60, RVE84,如图3 所示,被用于考察表征元尺寸对宏观塑性--损伤--愈合效应表征的影响. 每一个表征元尺寸是 l × l n r 39 ].
文献[12 ]详细讨论了二阶计算均匀化方法下所构造混合有限元的收敛性以及不需要宏观唯象本构与破坏模型,可以模拟颗粒 材料失效与捕捉应变局部化现象.
图3 相同介观结构但不同尺寸的表征元
Fig. 3 Three samples of RVE with different RVE sizes but the same regular configuration
本文以每一个积分点处累积的塑性及损伤耗散能密度及愈合能密度作为内状态变量表征宏观塑性、损伤与愈合,并定量比较 它们对颗粒材料破坏的效应.
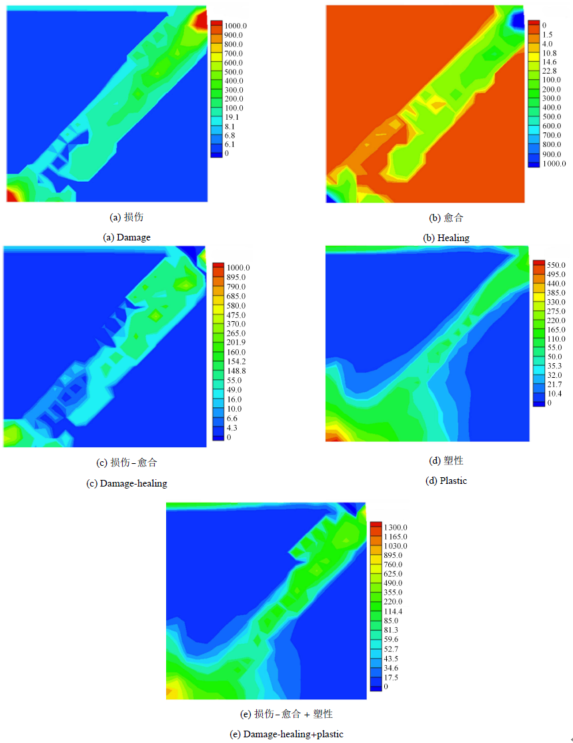
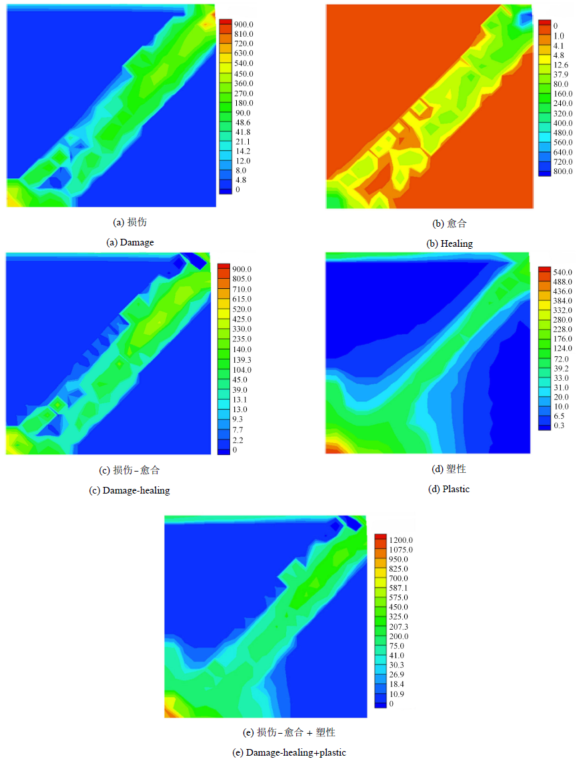
图4~图7 所示分别为采用表征元RVE40, RVE60, RVE84的方板应变局部化问题模拟加载结束时位移载荷曲线与耗散能密度分布云图. 颗粒材料等价梯度增强Cosserat连续体宏观损伤--愈合现象的介观机理为表征元内颗粒接触丧失与再生和直接相邻颗粒 间接触取向的改变,以及相伴随的表征元体积增大或减小,这些因素的综合将导致连续体局部材料点处弹性刚度的降低(损伤)或增大 (愈合),塑性耗散的介观机理为表征元内颗粒在接触点处的耗散性相对滑移、滚动. 颗粒材料等价梯度增强Cosserat连续体软化结束时即加载结束时,方板损 伤--愈合以及塑性耦合过程的热力学耗散主要集中在应变局 部化带. 对比图5 (c)、图5 (d)至图7 (c)、图7 (d),可以看到,表征元对应的等价梯度增强Cosserat连续体材料点处,表征颗粒间耗散性滑移、 滚动的塑性演化首先发生,表征颗粒间接触丧失的等价梯度增强Cosserat连续体局部点的体积膨胀与净损伤演化随后发生.
图4 位移载荷曲线
Fig. 4 Curves of load-displacement
图5 RVE40加载结束耗散能与愈合能密度分布(N/m)
Fig. 5 Contours of density of dissipative and healing energy distribution in the square panel at the end of the load history obtained by RVE40 (N/m)
图6 RVE60加载结束耗散能与愈合能密度分布(N/m)
Fig. 6 Contours of density of dissipative and healing energy distribution in the square panel at the end of the load history obtained by RVE60 (N/m)
图7 RVE84加载结束耗散能与愈合能密度分布(N/m)
Fig. 7 Contours of density of dissipative and healing energy distribution in the square panel at the end of the load history obtained by RVE84 (N/m)
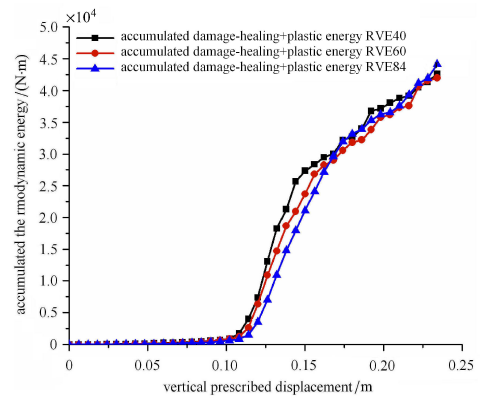
图8 所示为采用RVE40, RVE60, RVE84等3种具有相同介观结构而不同尺寸表征元样本的方板全域随加载过程的塑性总耗散能、 净损伤总耗散能与塑性--净损伤总耗散能的演变曲线. 可以看到,当采用RVE40样本时,导致结构失效的总净损伤耗散能远小于总塑性耗散能;当采用RVE60样本时,总净损伤耗散 能尚小于总塑性耗散能,但已较接近;而在采用RVE84样本的情况下,总净损伤耗散能与总塑性耗散能基本持平. 从这一方面看,表征元的大小对表征结果是有影响的.
另一方面,图9 所示为分别采用RVE40, RVE60和RVE84三种样本情况下方板的塑性--净损伤总耗散能随加载过程 的演变曲线比较. 从图9 可以看出,3条曲线比较接近,特别是在软化后直至加载结束这一后软化阶段的总耗散能曲线重合很好. 从这一方面看,表征结果并不病态地依赖于表征元尺寸. 图4 显示,分别采用RVE40, RVE60和RVE84三种样本情况下方板的外力耗散功十分接近,表明本文多尺度表征工作所基于的协同(concurrent)二阶计算 均匀化过程的颗粒材料结构多尺度模拟[11 ,12 ] 结果的可靠性,也即多尺度模拟结果不应病态地依赖于表征元的(窗口)尺寸. 图9 所给出的多尺度表征结果与图4 显示的多尺度模拟结果比较,验证了本文工作在数值误差意义上近似满足了结构的外力 耗散功模拟结果应等于结构的内耗散能表征结果这一基本要求,表明了本文提出的基于一致二阶计算均匀化过程的颗粒材料 塑性--损伤--愈合多尺度表征方法的有 效性.
图8 由所有积分点处耗散能密度累计的方板塑性、净损伤和总耗散能随加载过程的演化
Fig. 8 Evolutions of accumulated net damage, plasticity and total dissipative energies added up from those associated to all integration points of the square panel with increasing prescribed vertical displacement
图9 由所有积分点处耗散能密度累计的方板总耗散能随加载过程的演化
Fig. 9 Evolution of accumulated total dissipative energies added up from those associated to all integration points of the square panel with increasing prescribed vertical displacement
5 结论
颗粒材料在宏观和介观尺度分别模型化为梯度增强Cosserat连续体和离散颗粒集合体. 本文基于颗粒材料力学行为的协同二阶计算均匀化模拟,对具有离散颗粒介观结构的表征元建立了等价梯度增强Cosserat连续体的增量非线性本构关系.
在颗粒材料热动力学理论框架下,定义了基于介观结构与介观力学响应的塑性应变以及各向异性损伤、愈合因子张量和综合了各向异性损伤、愈合效应的净损伤因子张量,提出了以净损伤和塑性耗散能(标量)表示的多尺度表征方法. 应变局部化的数值例题结果显示了所提出表征方法的有效性.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
Alonso-marroquin F Static equation of the Cosserat continuum derived from intra-granular stress
. Granular Matter , 2011 , 13 (3 ): 189 -196
[本文引用: 1]
[2]
Chang CS Kuhn MR On virtual work and stress in granular media
.International Journal of Solids and Structures , 2005 , 42 (13 ): 3773 -3793
[本文引用: 1]
[3]
D’Addetta GA Ramm E A particle center based homogenization strategy for granular assemblies
.Engineering Computation , 2004 , 21 (2-3-4 ): 360 -383
[本文引用: 1]
[4]
Li XK Liu QP Zhang JB A micro-macro homogenization approach for discrete particle assembly Cosserate continuum modeling of granular materials
.International Journal of Solids and Structures , 2010 , 47 (2 ): 291 -303
[本文引用: 2]
[5]
Ehlers W Ramm E Diebels S et al .From particle ensembles to Cosserat continua: Homogenization of contact forces towards stresses and couple stresses
.International Journal of Solids and Structures , 2003 , 40 (24 ): 6681 -6702
[本文引用: 1]
[6]
Kruyt NP Statics and kinematics of discrete Cosserat-type granular materials
. International Journal of Solids and Structures , 2003 , 40 (3 ): 511 -534
[本文引用: 1]
[7]
Pasternak E Muhlhaus HB Generalised homogenisation procedures for granular materials
.Journal of Engineering Mathematics , 2005 , 52 (1-3 ): 199 -229
[本文引用: 1]
[8]
Qu J Cherkaoui M Fundamentals of Micromechanics of Solids
. New Jersey: Wiley , 2006
[本文引用: 1]
[9]
Li XK Liu QP A version of Hill’s lemma for Cosserat continuum
.Acta Mechanica Sinica , 2009 , 25 : 499 -506
[本文引用: 2]
[10]
Li XK Zhang JB Zhang X Micro-macro homogenization of gradient-enhanced Cosserat media
.European Journal of Mechanics A , 2011 , 30 (3 ): 362 -372
[本文引用: 1]
[11]
Li XK Zhang X Zhang JB A generalized Hill’s lemma and micromechanically based macroscopic constitutive model for heterogeneous granular materials
.Computer Methods in Applied Mechanics and Engineering , 2010 , 199 (49-52 ): 3137 -3152
[本文引用: 4]
[12]
Li XK Liang YB Quan QL et al .A mixed finite element procedure of gradient Cosserat continuum for second-order computational homogenization of granular materials
.Computational Mechanics , 2014 , 54 (5 ): 1331 -1356
[本文引用: 3]
[13]
Kachanov L Time rupture under creep conditions
.Izvestiya Akademii Nauk SSSR, Otdelenie Tekhnicheskikh Nauk , 1958 8 (8 ): 26 -31
[本文引用: 1]
[14]
Lemaitre J Chaboche JL. Mechanics of Solid Materials. Cambridge : Cambridge University Press , 1990
[本文引用: 1]
[15]
唐炳涛 . 基于连续体损伤理论的硼钢高温成形极限确定法
. 力学学报 , 2016 , 48 (1 ): 146 -153
[本文引用: 1]
(Tang Bingtao Prediction of forming limit of boron steel at elevated temperatrue based on CDM theory
.Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (1 ): 146 -153 (in Chinese))
[本文引用: 1]
[16]
Chaboche JL Continuum damage mechanics: Part I: General concept, Part II damage growth, crack initiation and crack growth
.Journal of Applied Mechanics , 1988 , 55 (3 ): 59 -71
[本文引用: 1]
[17]
Chow CL Wang J An anisotropic theory of elasticity for continuum damage mechanics
.International Journal of Fracture , 1987 , 33 (1 ): 3 -16
[本文引用: 1]
[18]
Ju JW On energy-based coupled elastoplastic damage theories: constitutive modeling and computational aspects
.International Journal of Solids and Structures , 1989 , 25 (7 ): 803 -833
[本文引用: 1]
[19]
Simo JC Ju JW Strain-based and stress-based continuum damage models, part I: Formulation
.International Journal of Solids and Structures , 1987 , 23 : 821 -840
[本文引用: 1]
[20]
Ladeveze P LeDantec E. Damage modelling of the elementary ply for laminated composites
.Composites Science and Technology , 1992 , 43 (3 ): 257 -267
[本文引用: 1]
[21]
Darabi MK Al-Rub RKA Little DN A continuum damage mechanics framework for modeling micro-damage healing
.International Journal of Solids and Structures , 2012 , 49 (3-4 ): 492 -513
[本文引用: 1]
[22]
Herbst O Luding S Modeling particulate self-healing materials and application to uni-axial compression
.International Journal of Fracture , 2008 , 154 (1-2 ): 87 -103
[本文引用: 1]
[23]
Mergheim J Steinmann P Phenomenological modelling of self-healing polymers based on integrated healing agents
.Computational Mechanics , 2013 , 52 (3 ): 681 -692
[本文引用: 1]
[24]
Aliko-Benteza A Doblaré M Chemical-diffusive modeling of the self-healing behavior in concrete
. International Journal of Solid and Structures , 2015 , 69-70 : 392 -402
[本文引用: 1]
[25]
陈洁 ,刘剑兴 ,姜德义 等 . 围压作用下岩盐应变与损伤恢复试验研究
. 岩土力学 ,2016 , 37 (1 ): 105 -112
[本文引用: 1]
(Chen Jie Liu Jianxing Jiang Deyi et al .An experimental study of strain and damage recovery of salt rock under confining pressures
. Rock and Soil Mechanics 2016 , 37 (1 ): 105 -112 (in Chinese))
[本文引用: 1]
[26]
Barbero EJ Greco F Lonetti P Continuum damage-healing mechanics with application to self-healing composites
.International Journal of Damage Mechanics , 2005 , 14 (1 ): 51 -81
[本文引用: 2]
[27]
Voyiadjis GZ Shojaei A Li G A thermodynamic consistent damage and healing model for self healing materials
.International Journal of Plasticity , 2011 , 27 (7 ): 1025 -1044
[本文引用: 1]
[28]
Voyiadjis GZ Shojaei A Li GQ et al .Continuum damage-healing mechanics with introduction to new healing variables
. International Journal of Damage Mechanics , 2012 , 21 (3 ): 391 -419
[本文引用: 1]
[29]
Voyiadjis GZ Kattan PI Healing and super healing in continuum damage mechanics
. International Journal of Damage Mechanics , 2014 , 23 (2 ): 245 -260
[本文引用: 1]
[30]
张浪平 ,尹祥础 ,梁乃刚 . 地震条件下损伤--愈合模型的初步研究
. 岩土力学与工程学报 ,2008 , 27 (2 ): 3956 -3962
[本文引用: 1]
(Zhang Langping Yin Xiangchu Liang Naigang Preliminary study on damage-healing model under earthquake
. Chinese Journal of Rock Mechanics and Engineering 2008 , 27 (2 ): 3956 -3962 (in Chinese))
[本文引用: 1]
[31]
Ju JW Yuan KY Kuo AW Novel strain energy coupled elastoplastic damage and healing models for geomaterials-Part I: Formulations
.International Journal of Damage Mechanics , 2012 21 (4 ): 525 -549
[本文引用: 2]
[32]
Ju JW Yuan KY New strain energy based coupled elastoplastic two-parameter damage and healing models for earth moving processes
.International Journal of Damage Mechanics , 2012 , 21 (7 ): 989 -1019
[本文引用: 2]
[33]
屈家旺 ,刘泉生 ,何军 等 . 泥岩弹塑性损伤--愈合模型研究
. 岩土力学与工程学报 , 2014 , 33 (1 ): 3192 -3197
[本文引用: 1]
(Qu Jiangwang Liu Quansheng He Jun et al .Study of elastoplastic damage-healing model for argillite,
Chinese Journal of Rock Mechanics and Engineering 2014 , 33 (1 ): 3192 -3197 (in Chinese))
[本文引用: 1]
[34]
Li XK Duxbury PD Lyons L Coupled creep-elastoplastic-damage analysis for isotropic and anisotropic nonlinear materials
.International Journal of Solids and Structure , 1994 , 31 (9 ), 1181 -1206
[本文引用: 1]
[35]
Li XK Du YY Duan QL Micromechanically informed constitutive model and anisotropic damage characterization of Cosserat continuumfor granular materials
.International Journal of Damage Mechanics , 2013 , 22 (5 ), 643 -682
[本文引用: 2]
[36]
付云伟 ,倪新华 ,刘协权 等 . 颗粒缺陷相互作用下复合材料的细观损伤模型
. 力学学报 , 2016 , 48 (6 ): 1334 -1342
[本文引用: 1]
(Fu Yunwei Ni Xinhua Liu Xiequan et al .Micro-damage model of composite materials with particle and defect interaction
.Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (6 ): 1334 -1342 (in Chinese))
[本文引用: 1]
[37]
郭洪宝 , 王波 , 贾普荣 等 . 平纹编织陶瓷基复合材料面内剪切细观损伤行为研究
. 力学学报 , 2016 , 48 (2 ): 361 -368
[本文引用: 1]
(Guo Hongbao Wang Bo Jia Purong et al .Mesoscopic damage behaviors of plain woven ceramic composite under in-plane shear loading
.Chinese Journal of Theoretical and Applied Mechanics 2016 , 48 (2 ): 361 -368 (in Chinese))
[本文引用: 1]
[38]
Li XK Du YY Duan QL et al .Thermodynamic framework for damage-healing-plasticity of granular materials and net damage variable,
International Journal of Damage Mechanics , 2016 , 25 (2 ): 153 -177
[本文引用: 2]
[39]
Li XK Wang ZH Mixed FEM-crushable DEM nested scheme in second-order computational homogenization for granular materials
.International Journal of Geomechanics , 2016 , 16 (5 ): C4016004
[本文引用: 1]
Static equation of the Cosserat continuum derived from intra-granular stress
1
2011
... 在介观尺度上颗粒材料的每个离散颗粒具有独立的旋转自由度与平动自由度,在接触点处能同时传递力和力偶. 因而在多尺度分析 中,它在宏观尺度上模型化为Cosserat连续体,而不是Cauchy连续 体[1 ,2 ,3 ,4 ,5 ,6 ,7 ] . 非均质材料的介--宏观计算均匀化模拟基于Hill定理,据此可以给定表征元(representation volume element, RVE)的静力学或运动学容许边界条件,使得Hill-Mendal宏--介观能量等价条件得到满足[8 ,9 ] . ...
On virtual work and stress in granular media
1
2005
... 在介观尺度上颗粒材料的每个离散颗粒具有独立的旋转自由度与平动自由度,在接触点处能同时传递力和力偶. 因而在多尺度分析 中,它在宏观尺度上模型化为Cosserat连续体,而不是Cauchy连续 体[1 ,2 ,3 ,4 ,5 ,6 ,7 ] . 非均质材料的介--宏观计算均匀化模拟基于Hill定理,据此可以给定表征元(representation volume element, RVE)的静力学或运动学容许边界条件,使得Hill-Mendal宏--介观能量等价条件得到满足[8 ,9 ] . ...
A particle center based homogenization strategy for granular assemblies
1
2004
... 在介观尺度上颗粒材料的每个离散颗粒具有独立的旋转自由度与平动自由度,在接触点处能同时传递力和力偶. 因而在多尺度分析 中,它在宏观尺度上模型化为Cosserat连续体,而不是Cauchy连续 体[1 ,2 ,3 ,4 ,5 ,6 ,7 ] . 非均质材料的介--宏观计算均匀化模拟基于Hill定理,据此可以给定表征元(representation volume element, RVE)的静力学或运动学容许边界条件,使得Hill-Mendal宏--介观能量等价条件得到满足[8 ,9 ] . ...
A micro-macro homogenization approach for discrete particle assembly Cosserate continuum modeling of granular materials
2
2010
... 在介观尺度上颗粒材料的每个离散颗粒具有独立的旋转自由度与平动自由度,在接触点处能同时传递力和力偶. 因而在多尺度分析 中,它在宏观尺度上模型化为Cosserat连续体,而不是Cauchy连续 体[1 ,2 ,3 ,4 ,5 ,6 ,7 ] . 非均质材料的介--宏观计算均匀化模拟基于Hill定理,据此可以给定表征元(representation volume element, RVE)的静力学或运动学容许边界条件,使得Hill-Mendal宏--介观能量等价条件得到满足[8 ,9 ] . ...
... 经典Cosserat连续体的Hill定理表明[4 ,9 ] ,宏观Cosserat连续体仅能下传与施加均一性宏观应变场于表征元边界. 作用于表征 元均一宏观应变场的合理性基于尺度分离概念,考虑到表征元尺寸并非远小于宏观连续体有限元分析的特征尺寸,特别是在高宏观应 变梯度(如应变局部化)区域尺度分离条件不再成立. 为施加非均一宏观应变场于表征元边界,要求在宏观尺度采用梯度增强Cosserat连续体模型 [10 ] ,并发展了相应的二阶计算均 匀化方法 [11 ] 和在宏--介观尺度的混合元--离散元嵌套算法 [12 ] . ...
From particle ensembles to Cosserat continua: Homogenization of contact forces towards stresses and couple stresses
1
2003
... 在介观尺度上颗粒材料的每个离散颗粒具有独立的旋转自由度与平动自由度,在接触点处能同时传递力和力偶. 因而在多尺度分析 中,它在宏观尺度上模型化为Cosserat连续体,而不是Cauchy连续 体[1 ,2 ,3 ,4 ,5 ,6 ,7 ] . 非均质材料的介--宏观计算均匀化模拟基于Hill定理,据此可以给定表征元(representation volume element, RVE)的静力学或运动学容许边界条件,使得Hill-Mendal宏--介观能量等价条件得到满足[8 ,9 ] . ...
Statics and kinematics of discrete Cosserat-type granular materials
1
2003
... 在介观尺度上颗粒材料的每个离散颗粒具有独立的旋转自由度与平动自由度,在接触点处能同时传递力和力偶. 因而在多尺度分析 中,它在宏观尺度上模型化为Cosserat连续体,而不是Cauchy连续 体[1 ,2 ,3 ,4 ,5 ,6 ,7 ] . 非均质材料的介--宏观计算均匀化模拟基于Hill定理,据此可以给定表征元(representation volume element, RVE)的静力学或运动学容许边界条件,使得Hill-Mendal宏--介观能量等价条件得到满足[8 ,9 ] . ...
Generalised homogenisation procedures for granular materials
1
2005
... 在介观尺度上颗粒材料的每个离散颗粒具有独立的旋转自由度与平动自由度,在接触点处能同时传递力和力偶. 因而在多尺度分析 中,它在宏观尺度上模型化为Cosserat连续体,而不是Cauchy连续 体[1 ,2 ,3 ,4 ,5 ,6 ,7 ] . 非均质材料的介--宏观计算均匀化模拟基于Hill定理,据此可以给定表征元(representation volume element, RVE)的静力学或运动学容许边界条件,使得Hill-Mendal宏--介观能量等价条件得到满足[8 ,9 ] . ...
Fundamentals of Micromechanics of Solids
1
2006
... 在介观尺度上颗粒材料的每个离散颗粒具有独立的旋转自由度与平动自由度,在接触点处能同时传递力和力偶. 因而在多尺度分析 中,它在宏观尺度上模型化为Cosserat连续体,而不是Cauchy连续 体[1 ,2 ,3 ,4 ,5 ,6 ,7 ] . 非均质材料的介--宏观计算均匀化模拟基于Hill定理,据此可以给定表征元(representation volume element, RVE)的静力学或运动学容许边界条件,使得Hill-Mendal宏--介观能量等价条件得到满足[8 ,9 ] . ...
A version of Hill’s lemma for Cosserat continuum
2
2009
... 在介观尺度上颗粒材料的每个离散颗粒具有独立的旋转自由度与平动自由度,在接触点处能同时传递力和力偶. 因而在多尺度分析 中,它在宏观尺度上模型化为Cosserat连续体,而不是Cauchy连续 体[1 ,2 ,3 ,4 ,5 ,6 ,7 ] . 非均质材料的介--宏观计算均匀化模拟基于Hill定理,据此可以给定表征元(representation volume element, RVE)的静力学或运动学容许边界条件,使得Hill-Mendal宏--介观能量等价条件得到满足[8 ,9 ] . ...
... 经典Cosserat连续体的Hill定理表明[4 ,9 ] ,宏观Cosserat连续体仅能下传与施加均一性宏观应变场于表征元边界. 作用于表征 元均一宏观应变场的合理性基于尺度分离概念,考虑到表征元尺寸并非远小于宏观连续体有限元分析的特征尺寸,特别是在高宏观应 变梯度(如应变局部化)区域尺度分离条件不再成立. 为施加非均一宏观应变场于表征元边界,要求在宏观尺度采用梯度增强Cosserat连续体模型 [10 ] ,并发展了相应的二阶计算均 匀化方法 [11 ] 和在宏--介观尺度的混合元--离散元嵌套算法 [12 ] . ...
Micro-macro homogenization of gradient-enhanced Cosserat media
1
2011
... 经典Cosserat连续体的Hill定理表明[4 ,9 ] ,宏观Cosserat连续体仅能下传与施加均一性宏观应变场于表征元边界. 作用于表征 元均一宏观应变场的合理性基于尺度分离概念,考虑到表征元尺寸并非远小于宏观连续体有限元分析的特征尺寸,特别是在高宏观应 变梯度(如应变局部化)区域尺度分离条件不再成立. 为施加非均一宏观应变场于表征元边界,要求在宏观尺度采用梯度增强Cosserat连续体模型 [10 ] ,并发展了相应的二阶计算均 匀化方法 [11 ] 和在宏--介观尺度的混合元--离散元嵌套算法 [12 ] . ...
A generalized Hill’s lemma and micromechanically based macroscopic constitutive model for heterogeneous granular materials
4
2010
... 经典Cosserat连续体的Hill定理表明[4 ,9 ] ,宏观Cosserat连续体仅能下传与施加均一性宏观应变场于表征元边界. 作用于表征 元均一宏观应变场的合理性基于尺度分离概念,考虑到表征元尺寸并非远小于宏观连续体有限元分析的特征尺寸,特别是在高宏观应 变梯度(如应变局部化)区域尺度分离条件不再成立. 为施加非均一宏观应变场于表征元边界,要求在宏观尺度采用梯度增强Cosserat连续体模型 [10 ] ,并发展了相应的二阶计算均 匀化方法 [11 ] 和在宏--介观尺度的混合元--离散元嵌套算法 [12 ] . ...
... 根据Hill定理、满足Hill-Mandel能量条件而应施加于表征元边界离散颗粒处的边界条件为 [11 ] ...
... 其中 D t e [11 ] 的弹性模量张量, Δ Λ ̅ p Δ Ξ ̅ p
... 另一方面,图9 所示为分别采用RVE40, RVE60和RVE84三种样本情况下方板的塑性--净损伤总耗散能随加载过程 的演变曲线比较. 从图9 可以看出,3条曲线比较接近,特别是在软化后直至加载结束这一后软化阶段的总耗散能曲线重合很好. 从这一方面看,表征结果并不病态地依赖于表征元尺寸. 图4 显示,分别采用RVE40, RVE60和RVE84三种样本情况下方板的外力耗散功十分接近,表明本文多尺度表征工作所基于的协同(concurrent)二阶计算 均匀化过程的颗粒材料结构多尺度模拟[11 ,12 ] 结果的可靠性,也即多尺度模拟结果不应病态地依赖于表征元的(窗口)尺寸. 图9 所给出的多尺度表征结果与图4 显示的多尺度模拟结果比较,验证了本文工作在数值误差意义上近似满足了结构的外力 耗散功模拟结果应等于结构的内耗散能表征结果这一基本要求,表明了本文提出的基于一致二阶计算均匀化过程的颗粒材料 塑性--损伤--愈合多尺度表征方法的有 效性. ...
A mixed finite element procedure of gradient Cosserat continuum for second-order computational homogenization of granular materials
3
2014
... 经典Cosserat连续体的Hill定理表明[4 ,9 ] ,宏观Cosserat连续体仅能下传与施加均一性宏观应变场于表征元边界. 作用于表征 元均一宏观应变场的合理性基于尺度分离概念,考虑到表征元尺寸并非远小于宏观连续体有限元分析的特征尺寸,特别是在高宏观应 变梯度(如应变局部化)区域尺度分离条件不再成立. 为施加非均一宏观应变场于表征元边界,要求在宏观尺度采用梯度增强Cosserat连续体模型 [10 ] ,并发展了相应的二阶计算均 匀化方法 [11 ] 和在宏--介观尺度的混合元--离散元嵌套算法 [12 ] . ...
... 文献[12 ]详细讨论了二阶计算均匀化方法下所构造混合有限元的收敛性以及不需要宏观唯象本构与破坏模型,可以模拟颗粒 材料失效与捕捉应变局部化现象. ...
... 另一方面,图9 所示为分别采用RVE40, RVE60和RVE84三种样本情况下方板的塑性--净损伤总耗散能随加载过程 的演变曲线比较. 从图9 可以看出,3条曲线比较接近,特别是在软化后直至加载结束这一后软化阶段的总耗散能曲线重合很好. 从这一方面看,表征结果并不病态地依赖于表征元尺寸. 图4 显示,分别采用RVE40, RVE60和RVE84三种样本情况下方板的外力耗散功十分接近,表明本文多尺度表征工作所基于的协同(concurrent)二阶计算 均匀化过程的颗粒材料结构多尺度模拟[11 ,12 ] 结果的可靠性,也即多尺度模拟结果不应病态地依赖于表征元的(窗口)尺寸. 图9 所给出的多尺度表征结果与图4 显示的多尺度模拟结果比较,验证了本文工作在数值误差意义上近似满足了结构的外力 耗散功模拟结果应等于结构的内耗散能表征结果这一基本要求,表明了本文提出的基于一致二阶计算均匀化过程的颗粒材料 塑性--损伤--愈合多尺度表征方法的有 效性. ...
Time rupture under creep conditions
1
1958
... 塑性的基本特征是连续体变形的不可恢复性以及在塑性变形过程中所做的塑性功的不可逆性. 经典连续损伤力学中材料损伤定义为 以弹性模量张量表示的弹性刚度降低[13 ,14 ,15 ] . ...
1
1990
... 塑性的基本特征是连续体变形的不可恢复性以及在塑性变形过程中所做的塑性功的不可逆性. 经典连续损伤力学中材料损伤定义为 以弹性模量张量表示的弹性刚度降低[13 ,14 ,15 ] . ...
基于连续体损伤理论的硼钢高温成形极限确定法
1
2016
... 塑性的基本特征是连续体变形的不可恢复性以及在塑性变形过程中所做的塑性功的不可逆性. 经典连续损伤力学中材料损伤定义为 以弹性模量张量表示的弹性刚度降低[13 ,14 ,15 ] . ...
基于连续体损伤理论的硼钢高温成形极限确定法
1
2016
... 塑性的基本特征是连续体变形的不可恢复性以及在塑性变形过程中所做的塑性功的不可逆性. 经典连续损伤力学中材料损伤定义为 以弹性模量张量表示的弹性刚度降低[13 ,14 ,15 ] . ...
Continuum damage mechanics: Part I: General concept, Part II damage growth, crack initiation and crack growth
1
1988
... 材料塑性与损伤描述了不可逆的能量耗散过程. 在连续介质力学唯象方法中,塑性与损伤理论研究基于热动力学框架与引入以唯象 形式定义的内变量以定量描述材料内部微结构演变和所伴随的不可逆能量耗散[16 ,17 ,18 ,19 ,20 ] . ...
An anisotropic theory of elasticity for continuum damage mechanics
1
1987
... 材料塑性与损伤描述了不可逆的能量耗散过程. 在连续介质力学唯象方法中,塑性与损伤理论研究基于热动力学框架与引入以唯象 形式定义的内变量以定量描述材料内部微结构演变和所伴随的不可逆能量耗散[16 ,17 ,18 ,19 ,20 ] . ...
On energy-based coupled elastoplastic damage theories: constitutive modeling and computational aspects
1
1989
... 材料塑性与损伤描述了不可逆的能量耗散过程. 在连续介质力学唯象方法中,塑性与损伤理论研究基于热动力学框架与引入以唯象 形式定义的内变量以定量描述材料内部微结构演变和所伴随的不可逆能量耗散[16 ,17 ,18 ,19 ,20 ] . ...
Strain-based and stress-based continuum damage models, part I: Formulation
1
1987
... 材料塑性与损伤描述了不可逆的能量耗散过程. 在连续介质力学唯象方法中,塑性与损伤理论研究基于热动力学框架与引入以唯象 形式定义的内变量以定量描述材料内部微结构演变和所伴随的不可逆能量耗散[16 ,17 ,18 ,19 ,20 ] . ...
LeDantec E. Damage modelling of the elementary ply for laminated composites
1
1992
... 材料塑性与损伤描述了不可逆的能量耗散过程. 在连续介质力学唯象方法中,塑性与损伤理论研究基于热动力学框架与引入以唯象 形式定义的内变量以定量描述材料内部微结构演变和所伴随的不可逆能量耗散[16 ,17 ,18 ,19 ,20 ] . ...
A continuum damage mechanics framework for modeling micro-damage healing
1
2012
... 损伤力学的近期研究表明,包括颗粒材料在内的许多工程材料在一定条件下具备愈合与部分恢复它们的刚度的潜 能[21 ,22 ,23 ,24 ,25 ] . 需要拓展经典连续损伤力学理论,以计及具有非耗散本质的愈合过程 [26 ] . 大部分模拟愈合过程的本构模型基于唯象理论 [26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ] . Ju等[31 ,32 ] 首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型. ...
Modeling particulate self-healing materials and application to uni-axial compression
1
2008
... 损伤力学的近期研究表明,包括颗粒材料在内的许多工程材料在一定条件下具备愈合与部分恢复它们的刚度的潜 能[21 ,22 ,23 ,24 ,25 ] . 需要拓展经典连续损伤力学理论,以计及具有非耗散本质的愈合过程 [26 ] . 大部分模拟愈合过程的本构模型基于唯象理论 [26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ] . Ju等[31 ,32 ] 首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型. ...
Phenomenological modelling of self-healing polymers based on integrated healing agents
1
2013
... 损伤力学的近期研究表明,包括颗粒材料在内的许多工程材料在一定条件下具备愈合与部分恢复它们的刚度的潜 能[21 ,22 ,23 ,24 ,25 ] . 需要拓展经典连续损伤力学理论,以计及具有非耗散本质的愈合过程 [26 ] . 大部分模拟愈合过程的本构模型基于唯象理论 [26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ] . Ju等[31 ,32 ] 首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型. ...
Chemical-diffusive modeling of the self-healing behavior in concrete
1
2015
... 损伤力学的近期研究表明,包括颗粒材料在内的许多工程材料在一定条件下具备愈合与部分恢复它们的刚度的潜 能[21 ,22 ,23 ,24 ,25 ] . 需要拓展经典连续损伤力学理论,以计及具有非耗散本质的愈合过程 [26 ] . 大部分模拟愈合过程的本构模型基于唯象理论 [26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ] . Ju等[31 ,32 ] 首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型. ...
围压作用下岩盐应变与损伤恢复试验研究
1
2016
... 损伤力学的近期研究表明,包括颗粒材料在内的许多工程材料在一定条件下具备愈合与部分恢复它们的刚度的潜 能[21 ,22 ,23 ,24 ,25 ] . 需要拓展经典连续损伤力学理论,以计及具有非耗散本质的愈合过程 [26 ] . 大部分模拟愈合过程的本构模型基于唯象理论 [26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ] . Ju等[31 ,32 ] 首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型. ...
围压作用下岩盐应变与损伤恢复试验研究
1
2016
... 损伤力学的近期研究表明,包括颗粒材料在内的许多工程材料在一定条件下具备愈合与部分恢复它们的刚度的潜 能[21 ,22 ,23 ,24 ,25 ] . 需要拓展经典连续损伤力学理论,以计及具有非耗散本质的愈合过程 [26 ] . 大部分模拟愈合过程的本构模型基于唯象理论 [26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ] . Ju等[31 ,32 ] 首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型. ...
Continuum damage-healing mechanics with application to self-healing composites
2
2005
... 损伤力学的近期研究表明,包括颗粒材料在内的许多工程材料在一定条件下具备愈合与部分恢复它们的刚度的潜 能[21 ,22 ,23 ,24 ,25 ] . 需要拓展经典连续损伤力学理论,以计及具有非耗散本质的愈合过程 [26 ] . 大部分模拟愈合过程的本构模型基于唯象理论 [26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ] . Ju等[31 ,32 ] 首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型. ...
... [26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ]. Ju等[31 ,32 ] 首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型. ...
A thermodynamic consistent damage and healing model for self healing materials
1
2011
... 损伤力学的近期研究表明,包括颗粒材料在内的许多工程材料在一定条件下具备愈合与部分恢复它们的刚度的潜 能[21 ,22 ,23 ,24 ,25 ] . 需要拓展经典连续损伤力学理论,以计及具有非耗散本质的愈合过程 [26 ] . 大部分模拟愈合过程的本构模型基于唯象理论 [26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ] . Ju等[31 ,32 ] 首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型. ...
Continuum damage-healing mechanics with introduction to new healing variables
1
2012
... 损伤力学的近期研究表明,包括颗粒材料在内的许多工程材料在一定条件下具备愈合与部分恢复它们的刚度的潜 能[21 ,22 ,23 ,24 ,25 ] . 需要拓展经典连续损伤力学理论,以计及具有非耗散本质的愈合过程 [26 ] . 大部分模拟愈合过程的本构模型基于唯象理论 [26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ] . Ju等[31 ,32 ] 首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型. ...
Healing and super healing in continuum damage mechanics
1
2014
... 损伤力学的近期研究表明,包括颗粒材料在内的许多工程材料在一定条件下具备愈合与部分恢复它们的刚度的潜 能[21 ,22 ,23 ,24 ,25 ] . 需要拓展经典连续损伤力学理论,以计及具有非耗散本质的愈合过程 [26 ] . 大部分模拟愈合过程的本构模型基于唯象理论 [26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ] . Ju等[31 ,32 ] 首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型. ...
地震条件下损伤--愈合模型的初步研究
1
2008
... 损伤力学的近期研究表明,包括颗粒材料在内的许多工程材料在一定条件下具备愈合与部分恢复它们的刚度的潜 能[21 ,22 ,23 ,24 ,25 ] . 需要拓展经典连续损伤力学理论,以计及具有非耗散本质的愈合过程 [26 ] . 大部分模拟愈合过程的本构模型基于唯象理论 [26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ] . Ju等[31 ,32 ] 首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型. ...
地震条件下损伤--愈合模型的初步研究
1
2008
... 损伤力学的近期研究表明,包括颗粒材料在内的许多工程材料在一定条件下具备愈合与部分恢复它们的刚度的潜 能[21 ,22 ,23 ,24 ,25 ] . 需要拓展经典连续损伤力学理论,以计及具有非耗散本质的愈合过程 [26 ] . 大部分模拟愈合过程的本构模型基于唯象理论 [26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ] . Ju等[31 ,32 ] 首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型. ...
Novel strain energy coupled elastoplastic damage and healing models for geomaterials-Part I: Formulations
2
2012
... 损伤力学的近期研究表明,包括颗粒材料在内的许多工程材料在一定条件下具备愈合与部分恢复它们的刚度的潜 能[21 ,22 ,23 ,24 ,25 ] . 需要拓展经典连续损伤力学理论,以计及具有非耗散本质的愈合过程 [26 ] . 大部分模拟愈合过程的本构模型基于唯象理论 [26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ] . Ju等[31 ,32 ] 首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型. ...
... [31 ,32 ]首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型. ...
New strain energy based coupled elastoplastic two-parameter damage and healing models for earth moving processes
2
2012
... 损伤力学的近期研究表明,包括颗粒材料在内的许多工程材料在一定条件下具备愈合与部分恢复它们的刚度的潜 能[21 ,22 ,23 ,24 ,25 ] . 需要拓展经典连续损伤力学理论,以计及具有非耗散本质的愈合过程 [26 ] . 大部分模拟愈合过程的本构模型基于唯象理论 [26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ] . Ju等[31 ,32 ] 首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型. ...
... ,32 ]首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型. ...
泥岩弹塑性损伤--愈合模型研究
1
2014
... 损伤力学的近期研究表明,包括颗粒材料在内的许多工程材料在一定条件下具备愈合与部分恢复它们的刚度的潜 能[21 ,22 ,23 ,24 ,25 ] . 需要拓展经典连续损伤力学理论,以计及具有非耗散本质的愈合过程 [26 ] . 大部分模拟愈合过程的本构模型基于唯象理论 [26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ] . Ju等[31 ,32 ] 首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型. ...
泥岩弹塑性损伤--愈合模型研究
1
2014
... 损伤力学的近期研究表明,包括颗粒材料在内的许多工程材料在一定条件下具备愈合与部分恢复它们的刚度的潜 能[21 ,22 ,23 ,24 ,25 ] . 需要拓展经典连续损伤力学理论,以计及具有非耗散本质的愈合过程 [26 ] . 大部分模拟愈合过程的本构模型基于唯象理论 [26 ,27 ,28 ,29 ,30 ,31 ,32 ,33 ] . Ju等[31 ,32 ] 首先对岩土材料提出了一个新的弹塑性--损伤--愈合唯象耦合模型. ...
Coupled creep-elastoplastic-damage analysis for isotropic and anisotropic nonlinear materials
1
1994
... 需要指出的是,在损伤--塑性耦合分析的宏观唯象理论框架内,损伤现象一般假定为各向同性 [34 ] . 然而,对于包括颗粒 材料在内的具有非均质和复杂介观结构的材料,材料的损伤与愈合在本质上为各向异性. 各向异性来源于颗粒材料局部初始介观结构的各向异性以及由于颗粒材料力学响应导致的局部介观结构演变的各向异 性[35 ,36 ,37 ,38 ] . ...
Micromechanically informed constitutive model and anisotropic damage characterization of Cosserat continuumfor granular materials
2
2013
... 需要指出的是,在损伤--塑性耦合分析的宏观唯象理论框架内,损伤现象一般假定为各向同性 [34 ] . 然而,对于包括颗粒 材料在内的具有非均质和复杂介观结构的材料,材料的损伤与愈合在本质上为各向异性. 各向异性来源于颗粒材料局部初始介观结构的各向异性以及由于颗粒材料力学响应导致的局部介观结构演变的各向异 性[35 ,36 ,37 ,38 ] . ...
... 热力学框架下,与损伤--愈合因子张量增量 Δ d [35 ] ...
颗粒缺陷相互作用下复合材料的细观损伤模型
1
2016
... 需要指出的是,在损伤--塑性耦合分析的宏观唯象理论框架内,损伤现象一般假定为各向同性 [34 ] . 然而,对于包括颗粒 材料在内的具有非均质和复杂介观结构的材料,材料的损伤与愈合在本质上为各向异性. 各向异性来源于颗粒材料局部初始介观结构的各向异性以及由于颗粒材料力学响应导致的局部介观结构演变的各向异 性[35 ,36 ,37 ,38 ] . ...
颗粒缺陷相互作用下复合材料的细观损伤模型
1
2016
... 需要指出的是,在损伤--塑性耦合分析的宏观唯象理论框架内,损伤现象一般假定为各向同性 [34 ] . 然而,对于包括颗粒 材料在内的具有非均质和复杂介观结构的材料,材料的损伤与愈合在本质上为各向异性. 各向异性来源于颗粒材料局部初始介观结构的各向异性以及由于颗粒材料力学响应导致的局部介观结构演变的各向异 性[35 ,36 ,37 ,38 ] . ...
平纹编织陶瓷基复合材料面内剪切细观损伤行为研究
1
2016
... 需要指出的是,在损伤--塑性耦合分析的宏观唯象理论框架内,损伤现象一般假定为各向同性 [34 ] . 然而,对于包括颗粒 材料在内的具有非均质和复杂介观结构的材料,材料的损伤与愈合在本质上为各向异性. 各向异性来源于颗粒材料局部初始介观结构的各向异性以及由于颗粒材料力学响应导致的局部介观结构演变的各向异 性[35 ,36 ,37 ,38 ] . ...
平纹编织陶瓷基复合材料面内剪切细观损伤行为研究
1
2016
... 需要指出的是,在损伤--塑性耦合分析的宏观唯象理论框架内,损伤现象一般假定为各向同性 [34 ] . 然而,对于包括颗粒 材料在内的具有非均质和复杂介观结构的材料,材料的损伤与愈合在本质上为各向异性. 各向异性来源于颗粒材料局部初始介观结构的各向异性以及由于颗粒材料力学响应导致的局部介观结构演变的各向异 性[35 ,36 ,37 ,38 ] . ...
Thermodynamic framework for damage-healing-plasticity of granular materials and net damage variable,
2
2016
... 需要指出的是,在损伤--塑性耦合分析的宏观唯象理论框架内,损伤现象一般假定为各向同性 [34 ] . 然而,对于包括颗粒 材料在内的具有非均质和复杂介观结构的材料,材料的损伤与愈合在本质上为各向异性. 各向异性来源于颗粒材料局部初始介观结构的各向异性以及由于颗粒材料力学响应导致的局部介观结构演变的各向异 性[35 ,36 ,37 ,38 ] . ...
... 进一步,在颗粒材料热动力学框架 [38 ] 内定义了基于表征元介观力学信息的塑性应变以及各向异性损伤、愈合因子张量和 综合了各向异性损伤、愈合效应的净损伤因子张量. 进一步,以塑性、损伤耗散能与非耗散的愈合能等具有标量特征的内状态量表征并定量比较材料的塑性--损 伤--愈合效应. 应变局部化数值算例表明了基于介观力学信息的宏观梯度Cosserat连续体中塑性--损伤--愈合表征方 法的有效性. ...
Mixed FEM-crushable DEM nested scheme in second-order computational homogenization for granular materials
1
2016
... 有限元网格中,每一个积分点处配置一个初始构形相同的表征元. 3种具有相同规则介观结构,但具有不同尺寸的表征元, 分别命名为RVE40, RVE60, RVE84,如图3 所示,被用于考察表征元尺寸对宏观塑性--损伤--愈合效应表征的影响. 每一个表征元尺寸是 l × l n r 39 ]. ...