力学学报 2018 , 50 (2): 244-253 https://doi.org/10.6052/0459-1879-17-345

流体力学

错列角度对双圆柱涡激振动影响的数值模拟研究

段松长, 赵西增²⁾^,, 叶洲腾, 王凯鹏

浙江大学海洋学院,浙江舟山 316021

NUMERICAL STUDY OF STAGGERED ANGLE ON THE VORTEX-INDUCED VIBRATION OF TWO CYLINDERS

Duan Songchang, Zhao Xizeng²⁾^,, Ye Zhouteng, Wang Kaipeng

Ocean College, Zhejiang University, Zhoushan 316021, Zhejiang,China

中图分类号: P751,TB531

文献标识码: A

收稿日期: 2017-10-18

接受日期: 2017-10-18

网络出版日期: 2018-03-20

作者简介:

作者简介：2) 赵西增，教授，主要研究方向：波浪和建筑物的相互作用. E-mail: xizengzhao@zju.edu.cn

展开

摘要

为研究错列角度 $α$ 对双圆柱涡激振动问题的影响,采用自主研发的基于CIP (constrained interpolation profile)方法的数值模型,对雷诺数 $Re = 100$ 、错列角度 $α = 0 ∘ ~ 9 0 ∘$ (间隔15 #x00B0;)的等直径双圆柱涡激振动问题进行数值模拟. 模型在笛卡尔网格系统下建立,采用具有三阶精度的 CIP 方法求解 N-S (Navier--Stokes)方程,采用浸入边界法处理流--固耦合问题,避免了任意拉欧方法下的网格畸变和重叠动网格技术中的大量信息交换问题,保证了模型的计算效率. 重点分析不同错列角度 $α$ 上下游圆柱的升阻力系数、位移响应、涡脱频率和尾涡模态等. 结果表明：折合速度 $U r = 2.0 ~ 3.0$ 时,上下游圆柱升阻力随错列角度的增大基本呈单调增大的趋势; $U r = 5.0 ~ 8.0$ 时,随错列角度的增大,上下游圆柱阻力变化较小,升力呈“上凸”趋势,在 $α = 1 5 ∘ ~ 3 0 ∘$ 取得最大值; $U r = 10.0 ~ 13.0$ 时,随错列角度的增大,上下游圆柱阻力变化较小,升力呈“下凹”趋势,在 $α = 3 0 ∘ ~ 4 5 ∘$ 取得最小值,且柱体横流向振幅和升力没有明显的对应关系. 最后,结合尾涡模态对以上规律的成因进行分析. 研究结果可为相关海洋工程设计提供参考.

关键词： 错列双圆柱 ; 错列角度 ; CIP 方法 ; 涡激振动 ; Navier-Stokes 方程 ; 浸入边界法

Abstract

The vortex-induced vibration of two cylinders with the effect of the stagger angle is studied numerically. A finite difference model based on an in-house code named CIP (constraint interpolation profile) is utilized. The model is built on a Cartesian coordinate system, with the Navier-Stokes equation solved by a third-order accuracy CIP method. The fluid-structure interaction is modelled by an immersed boundary method. Based on the CIP model, two-dimensional flow past two equal-sized circular cylinders placed at Reynolds number ( $Re = 100$ ) with different stagger angle ( $α = 0 ∘ ~ 9 0 ∘$ with a 15 #x00B0; interval) is investigated. Main attention has been paid to the lift coefficient, drag coefficient, displacement response, vortex-shedding frequency and wake pattern of both cylinders. The results show that the drag coefficient and lift coefficient of both cylinders increase monotonically as the stagger angle increases when reduced velocity $U r = 2.0 ~ 3.0$ . For reduced velocity $U r = 5.0 ~ 8.0$ , with the increase of stagger angle, the drag coefficient of both cylinders changes slightly and the lift coefficient of both cylinders presents a “convex-like” trend and reaches maximum value at $α = 1 5 ∘ ~ 3 0 ∘$ . In the case of reduced velocity $U r = 10.0 ~ 13.0$ , with the increase of stagger angle, the drag coefficient of both cylinders also displays little change and the lift coefficients of both cylinders show a “concave-like” trend and reach minimum value at $α = 3 0 ∘ ~ 4 5 ∘$ . However, there is no obvious correspondence between the transverse oscillation amplitude and lift coefficient of cylinder as $U r = 10.0 ~ 13.0$ . Finally, the wake pattern of both cylinders is analyzed to explain above phenomenon. Above all, the present result could be helpful to the structure design of ocean engineering.

Keywords： staggered cylinders ; stagger angle ; CIP method ; vortex-induced vibration ; Navier-Stokes equation ; immersed boundary method

PDF (12108KB) 元数据多维度评价相关文章收藏文章

本文引用格式导出 EndNote Ris Bibtex

段松长, 赵西增, 叶洲腾, 王凯鹏. 错列角度对双圆柱涡激振动影响的数值模拟研究[J]. 力学学报, 2018, 50(2): 244-253 https://doi.org/10.6052/0459-1879-17-345

Duan Songchang, Zhao Xizeng, Ye Zhouteng, Wang Kaipeng. NUMERICAL STUDY OF STAGGERED ANGLE ON THE VORTEX-INDUCED VIBRATION OF TWO CYLINDERS[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(2): 244-253 https://doi.org/10.6052/0459-1879-17-345

引言

涡激振动问题发生在很多实际工程中,比如海洋立管、海底管线、高耸建筑等在受到风或海流的作用时,会因涡旋脱落而导致结构振动. 和静止圆柱绕流不同,当涡旋脱落频率接近柱体自振频率时,柱体会发生“锁定” 现象^[1]. “锁定”现象的发生会使结构物发生疲劳破坏,进而缩短结构物的寿命. 双圆柱涡激振动作为多柱体涡激振动的基础,除柱体和流体本身的特性外,柱体布置方式也会影响柱体的振动响应和流场状态. 如图1所示,仅在双圆柱涡激振动中就存在3种布置方式：串列( $α = 0^{\circ}$ )、并列 ( $α = 9 0^{\circ}$ )和错列 ( $0^{\circ} < α < 9 0^{\circ}$ ). 其中, $α$ 是两柱体中心连线和来流方向之间的夹角(锐角),下文中将其简称为“错列角度”.

显示原图| 下载原图ZIP| 生成PPT

图1 双柱体布置示意图

Fig. 1 Sketch of layout for two circular cylinders

涡激振动过程涉及湍流、流动分离、涡旋拓扑、物体振动和流固耦合等复杂问题,其数值分析的难点在于动边界的处理和流场的精确捕捉. Tonmurt^[2]利用任意拉欧数值方法对雷诺数 $Re = 100 ~ 140$ 范围的单圆柱涡激振动问题进行了系统研究,发现物体在运动时柱体表面网格的正交性不易保持,容易出现网格畸变问题. 近些年,对单圆柱涡激振动的研究集中在来流特性对振动结果的影响. 其中,剪切流对单圆柱涡激振动影响的相关研究可参考文献^[3,4,5],周期性振荡流对单圆柱涡激振动的影响可参考文献^[6,7]. 多柱体方面,Mittal等^[8]利用重叠网格技术研究了雷诺数 $Re = 100$ 和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力 $C_{d}$ 比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数 $Re = 100$ ,错列角度 $α \approx 7^{\circ}$ 双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度 $7.1 < U_{r} < 8.3$ 时,下游圆柱运动轨迹才是“8”字型. Borazjani和Sotiropoulos^[10]利用浸入边界法处理流固耦合问题,数值模拟了串列双圆柱涡激振动问题,发现串列布置柱体的振幅和升力要比单柱体大,且在不同的折合速度下分别呈现出“2S”和“2P”两种涡旋脱落模态. 吴晓笛等^[11]基于浸入边界--多松弛时间格子波尔兹曼通量求解法的弱耦合算法对串列双圆柱双自由度涡激振动问题进行了研究. 郭晓玲等^[12]采用任意拉格朗日--欧拉动网格方法对雷诺数 $Re = 150$ 串列双圆柱涡激振动问题进行了数值模拟. Williamson ^[13]通过模型试验对并列双圆柱涡激振动进行了研究,发现尾涡脱落存在两种方式,即同相同步. Chen等^[14]对雷诺数 $Re = 100$ 不同间距比下并列双圆柱涡激振动进行了数值模拟,发现当间距比大于4.0时,两圆柱之间的相互作用非常弱. 可见,关于双圆柱涡激振动的研究大多是在固定两柱体的布置方式下研究不同折合速度时的柱体响应. 而实际工程中,比如,两个近距离布置的高耸烟囱、海洋立管等,在不同的来流方向下就会呈现出不同错列角度的布置方式. 如何设计常风向或者常流向下最安全的错列角度 $α$ 是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度 $U_{r}$ 和错列角度 $0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}$ 下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态.

本文基于浸入边界方法的流固耦合技术,采用固定笛卡尔正交网格,在计算过程中无需更新网格,避免了重叠网格技术中的大量信息交换和任意拉欧方法中的网格畸变问题,同时可保证模型的高效率,使得模型在处理大位移的流固耦合计算中具有强大优越性. 为精确捕捉流场信息,在以前的工作中已将自主研发的紧致插值曲线方法模型应用于圆柱绕流问题^[15,16]和强迫振荡圆柱绕流问题^[17]的研究中,初步验证了该模型在处理复杂流动问题的准确性. 本文拟进一步拓展该模型的应用范围,对不同折合速度 $U_{r}$ 和错列角度 $α$ 下双圆柱涡激振动进行数值模拟,系统分析特定折合速度 $U_{r}$ 下柱体升阻力、位移响应和柱体后方尾涡模态随错列角度的变化规律,以期为相关海洋工程设计提供参考数据.

1 数值方法

涡激振动是一种流固耦合问题,需要考虑流场、结构物和流固耦合三个过程. 其中,流场模型考虑二维不可压缩流体,控制方程为N-S方程和质量守恒方程(连续性方程),其张量形式如下

$\partial u_{i} \partial x_{i} = 0 (1)$

$\partial u_{i} \partial t + u_{j} \partial u_{i} \partial x_{j} = - 1 ρ \partial p \partial x_{i} + 1 ρ \partial S_{ij} \partial x_{j} + f_{i} (2)$

其中, $i, j$ 是笛卡尔张量符号, $t, u_{j}, p, ρ$ 分别表示时间、流速、密度和动水压力, $f_{i}$ 是力源项, $S_{ij}$ 是黏性项,由下式定义

$S_{ij} = μ (\partial u_{i} \partial x_{j} + \partial u_{j} \partial x_{i})$ (3)

式中, $μ$ 表示黏性.

柱体结构可简化为一个质量--弹簧--阻尼系统,考虑横流向和顺流向的运动,其控制方程为

16mm $m \partial^{2} y \partial t^{2} + c \partial y \partial t + ky = F_{y} (4)$

16mm $m \partial^{2} x \partial t^{2} + c \partial x \partial t + kx = F_{x} (5)$

式中, $m, c$ 和 $k$ 分别表示柱体的质量、阻尼参数和弹簧刚度, $F_{y}$ 表示垂直于流向方向柱体的合力, $F_{x}$ 表示流向方向柱体的合力.

在直角坐标系下建立模型,采用多相流理论将计算域分为固相、液相两部分. 定义体积函数 $Φ_{n}$ 来区分固相和液相( $n = 1$ ,代表液相; $n = 2$ ,代表固相)并捕捉固--液界面. $Φ_{n}$ 满足如下公式

$\partial Φ_{12} \partial t + u_{i} \partial Φ_{12} \partial x_{i} = 0$ (6)

式中, $Φ_{12} = Φ_{1} + Φ_{2}$ ,并在一个网格内满足 $Φ_{1} + Φ_{2} = 1$ . 则网格内的流体特性可用下式表示

$γ = \sum_{n}^{=} ‍ Φ_{n} γ_{n}$ (7)

式中, $γ$ 表示密度 $ρ$ 或黏滞系数 $μ$ .

本文所采用的CIP方法模型,核心部分在于对流体控制方程(1)和(2)进行离散,过程分为3步：(1) 采用CIP方法^[18]求解对流项;(2) 采用中心差分法求解压力项外的非对流项;(3) 采用逐次超松驰迭代(successive over relaxation,SOR)方法进行压力速度耦合. 流固耦合边界采用浸入边界法(immersed boundary method,IBM) ^[19]处理.

显示原图| 下载原图ZIP| 生成PPT

图2 计算域及网格划分示意图

Fig. 2 Sketch of computational domain and mesh

通过对不同阻流比 $B$ ( $B = d / H$ , $H$ 为计算域宽度,单圆柱时 $d = D$ ,双圆柱时 $d = 2 D - h$ , $h$ 柱为两圆柱在横流向投影的重叠长度,如图1所示)单双圆柱涡激振动问题数值模拟,得知当阻流比小于10%时,本数值模型中阻流比对涡激振动特征参数的影响可忽略. 为保证结果可靠性,本文取阻流比 $B$ =5%. 计算区域及网格划分如图2所示. 上下边界的圆柱直径 $D = 1$ ,入口边界距上游圆柱圆心为10 $D$ ,上边界、下边界距上游圆柱圆心均为20 $D$ ,出口边界距上游圆柱圆心 25 $D$ . 对于双圆柱涡激振动而言,两柱体并列布置时阻流比达到最大值5%,可保证所有错列角度下阻流比的影响都可忽略. 数值模拟参数 $Re = 100$ ,折合速度 $U_{r} = 2.0 ~ 15.0$ ,间隔1.0,圆柱的质量比 $m^{*} = 4 m / (ρ f π D^{2}) = 2.0$ ,阻尼比 $ζ^{*} = 0$ . 为更好地捕捉柱体的运动和其周围的复杂流动现象,对柱体近壁面网格进行加密,最小网格设为 $Δ x = Δ y = D / 40$ . 计算流场的边界条件和初始条件设置如下：初始速度场设置为从左向右并保持均匀来流速度 $u = U$ , $v = 0$ ( $u, v$ 分别为 $x, y$ 方向的速度);初始压力场设定为零;出口边界为开边界 (自由出流);柱体表面采用无滑移边界;两侧壁面采用自由滑移边界. 通过对不同柱间距 $T$ 下错列双圆柱涡激振动进行数值模拟发现,当 $T < 3 D$ 时,两圆柱会出现碰撞现象. 为保证两柱体在振动过程中相互影响较大且不出现碰撞现象,综合选取中心间距 $T = 3 D$ .

2 模型验证

2.1 网格收敛性验证

为验证网格收敛性,本节选取雷诺数 $Re = 200$ 的单圆柱静止绕流作为算例,设置四套不同尺寸的网格 (mesh1, mesh2, mesh3, mesh4),其对应的最小网格尺寸分别为： $Δ x = Δ y = D / 50$ , $D / 40$ , $D / 25$ 和 $D / 10$ . 将计算出的柱体阻力系数均值 $C_{d . mean}$ 和无量纲涡旋脱落频率 $S_{t}$ 和文献[20,21,22]的结果进行对比,如表1所示. 可看出,mesh3和mesh4的阻力系数均值和无量纲涡旋脱落频率较其他结果偏小,mesh1和mesh2与其他文献的结果吻合较好,且mesh2的结果和文献[21]的结果相差最小. 表中RE 分别是阻力系数均值和无量纲涡脱频率相对mesh1结果的偏差. 可看出,mesh4的相对偏差较大,都在10%以上. 而mesh2结果的相对偏差都在2%以下,表明mesh2网格已具有收敛性. 综合考虑精度及计算效率,本文采用mesh2对接下来的工况进行计算.

表1 单圆柱绕流结果

Table 1 Result of flow past a singular circular cylinder

	Grids	$C_{d . mean}$ (RE)	$S_{t}$ (RE)
mesh1	407 800	1.313 5	0.193 4
mesh2	92 800	1.304 6(0.67%)	0.190 4(1.5%)
mesh3	32 175	1.291 1(1.7%)	0.185 5(4.08%)
mesh4	12 500	1.171 5(10.8%)	0.169 7 (12.2%)
Ref.[20]	—	1.336	0.194
Ref.[21]	—	1.3	0.196
Ref.[22]	—	1.32	0.1922

新窗口打开

2.2 单圆柱涡激振动

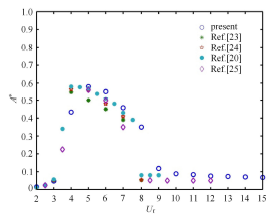
本节中选取质量比 $m^{*} = 2.0$ ,雷诺数 $Re = 100$ ,折合速度 $U_{r} = 2.0 ~ 15.0$ (间隔1.0)的单圆柱涡激振动工况作为算例,并将振幅比 $A^{*} = (Y_{\max} - Y_{\min}) / D$ 与文献[20,23-25]结果相比较,如图3. 其中, $Y_{\max}$ 和 $Y_{\min}$ 分别是柱体在一个响应周期内横流向的最大、最小位移. 如图3所示,当 $U_{r} = 5.0$ 时,振幅比 $A^{*} = 0.58$ ,达到最大值,意味着圆柱进入频率锁定状态,与及春宁等^[25]的结果吻合较好. 随折合速度的增大,振幅比逐渐变小,在 $U_{r} = 9.0$ 时,振幅比 $A^{*} = 0.117 8$ ,远小于锁定区间的振幅比,柱体脱离频率锁定区. 通过对比可看出,柱体振幅比随折合速度变化的规律和现有文献结果吻合较好.

显示原图| 下载原图ZIP| 生成PPT

图3 单圆柱涡激振动振幅比随折合速度变化情况

Fig. 3 Amplitude ratio versus reduced velocity in singular circular cylinder condition

3 结果与讨论

考虑到折合速度 $U_{r}$ 对柱体的振动响应有较大影响,本节首先对折合速度 $U_{r} = 2.0 ~ 13.0$ (间隔1.0)下不同错列角度的双圆柱涡激振动进行数值模拟,重点关注两柱体的阻力系数均值 $C_{d. mean}$ 和升力系数均方根 $C_{l . rms}$ . 为便于观察,按照图3中单圆柱振幅随折合速度的变化情况将折合速度分成(a)、(b)和(c)三个区域. 其中,区域(a)内的折合速度小于锁定区间对应的折合速度,即 $U_{r} = 2.0 ~ 3.0$ ;区域(b)内的折合速度处于锁定区间内,即 $U_{r} = 4.0 ~ 8.0$ ;区域(c)内的折合速度大于锁定区间对应的折合速度,即 $U_{r} = 9.0 ~ 13.0$ . 当折合速度 $U_{r} = 14.0$ 和15.0时两柱体出现了碰撞,本文暂不予考虑.

3.1 柱体升阻力系数

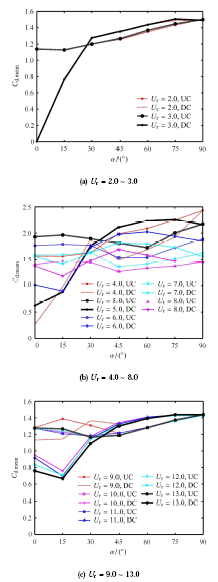
图4和图5分别是折合速度 $U_{r} = 2.0 ~ 13.0$ 不同错列角度上下游圆柱的阻力系数均值和升力系数均方根随错列角度的变化情况. 其中,(a)、(b)、(c)分别对应上文中的3个区域,“UC”代表上游圆柱,“DC”代表下游圆柱.

从图4和图5可看出,除了过渡区的折合速度 ( $U_{r} = 4.0$ 和9.0)外,其他折合速度下柱体升阻力随错列角度的变化规律在同一区域内具有相似性. 对于 $U_{r} = 2.0 ~ 3.0$ ,如图4(a)所示, $α = 0^{\circ}$ 时下游圆柱阻力几乎为零,说明上游圆柱尾流对下游圆柱的“屏蔽”作用^[25]较强,即下游圆柱处在上游圆柱的尾流中,来流速度较小导致下游圆柱阻力较小.

显示原图| 下载原图ZIP| 生成PPT

图4 折合速度 $U r = 2.0 ~ 13.0$ 上下游圆柱的阻力系数均值 $C d . mean$ 随错列角度的变化情况

Fig. 4 Mean value of drag coefficient versus stagger angle for different reduced velocities

显示原图| 下载原图ZIP| 生成PPT

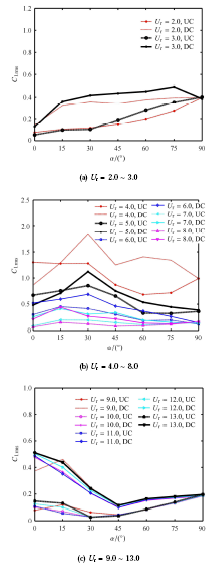
图5 折合速度 $U r = 2.0 ~ 13.0$ 上下游圆柱的升力系数均方根 $C l . rms$ 随错列角度的变化情况

Fig. 5 Root mean square lift coefficients versus stagger angle for different reduced velocities

随错列角度的增大,“屏蔽”作用逐渐减弱,下游圆柱阻力明显增加,在 $α = 9 0^{\circ}$ 时两柱体阻力相等. 和下游圆柱相比,上游圆柱的阻力随错列角度的变化较小. 如图5(a)所示,两柱体升力随错列角度的增大几乎都呈现单调增加的趋势. 另外,若固定错列角度,对比不同折合速度下两柱体的升阻力,可发现上下游柱体的阻力基本相等,而升力出现差异,说明折合速度对上下游柱体的阻力影响较小,对升力的影响较大. 对于 $U_{r} = 4.0 ~ 8.0$ ,如图4(b)所示,柱体阻力随错列角度变化规律上呈现的主要差异是“屏蔽”作用的弱化. 如图5(b)所示,两柱体的升力随错列角度的变大不再单调增大,而是呈“上凸”趋势,在 $α = 1 5^{\circ} ~ 3 0^{\circ}$ 取得最大值. 若固定错列角度,对比不同折合速度下柱体的升阻力,可发现随折合速度的增大,上下游圆柱所受升阻力逐渐减小,说明折合速度对上下游柱体升阻力的影响都较大.

对于 $U_{r} = 9.0 ~ 13.0$ ,如图4(c)所示,错列角度较小时上游圆柱对下游圆柱的“屏蔽”作用较弱,在错列角度 $α = 0^{\circ}$ 时下游圆柱阻力不是最小值. 如图5(c)所示,两柱体的升力随错列角度的增大呈“下凹”趋势,在 $α = 4 5^{\circ}$ 左右取得最小值. 若固定错列角度,对比不同折合速度下柱体的升阻力,可发现不同折合速度下上下游柱体的升阻力基本相等,说明折合速度对上下游柱体升阻力的影响都较小.

3.2 柱体振动响应、位移响应

为便于阐述上文中3种情况下上下游柱体的振动响应、位移响应随错列角度变化的情况,本节选取 $U_{r} = 3.0$ , 5.0和13.0的工况分别作为上述3种情况的特征工况进行分析. 图6给出了3个特征工况下两柱体横流向位移均方根(图6(a))、顺流向位移均值(图6(b))以及顺流向位移均方根(图6(c))随错列角度的变化情况. 其中,横、顺流向位移均方根大小分别反映了柱体在横流向和顺流向振动的剧烈程度,顺流向位移均值大小反映了柱体在顺流向上的平均偏移程度.

如图6(a) 和图6(b)所示, $U_{r} = 3.0$ 时,上下游圆柱的横流向位移均方根在 $α = 0^{\circ}$ 时最小,随错列角度的增大两柱体在横流向的振动程度都在增大,在 $α = 7 5^{\circ}$ 附近取得最大值,和柱体升力大小变化规律一致. 由于上游圆柱“屏蔽”作用的影响,下游圆柱的顺流向位移均值在 $α = 0^{\circ}$ 时几乎为零. 随错列角度的增大,下游圆柱的顺流向偏移程度逐渐变大,并逐渐接近上游圆柱,总体上和柱体阻力大小变化规律一致.

显示原图| 下载原图ZIP| 生成PPT

图6 不同折合速度上下游柱体位移响应随错列角度的变化情况

Fig. 6 Displacement response of both cylinders with stagger angle under different reduced velocity $U r$

显示原图| 下载原图ZIP| 生成PPT

图7 不同折合速度上下游圆柱涡旋脱落主导频率随错列角度的变化情况

Fig. 7 The main vortex shedding frequency of both cylinders versus stagger angle under different reduced velocities

$U_{r} = 5.0$ 时,上下游柱体的横流向位移均方根及顺流向位移均值随错列角度变化的规律分别和升、阻力的变化规律一致. 其中,上游圆柱的横流向位移均方根和柱体升力在 $α = 6 0^{\circ}$ 左右同时取得最小值,下游圆柱的横流向位移均方根和柱体升力在 $α = 3 0^{\circ}$ 左右同时取得最大值,而后随错列角度的增大而减小. 对于顺流向位移均值,下游圆柱在 $α = 0^{\circ}$ 时最小,并随错列角度的增大先增大后减小,在 $α = 6 0^{\circ}$ 左右取得最大值. 而上游圆柱的顺流向位移均值随错列角度的变化波动较小,在阻力最小即 $α = 6 0^{\circ}$ 时取得最小值. $U_{r} = 13.0$ 时,上下游圆柱顺流向位移均值和所受阻力随错列角度变化规律一致,但柱体的横流向位移均方根不再和升力变化规律一致. 下游圆柱升力在 $α = 4 5^{\circ}$ 左右取得最小值时,其横流向位移均方根却不是最小值. 总体来说,下游圆柱在错列角度较小时( $α < 4 5^{\circ}$ )其横流向位移均方根普遍较大,而错列角度较大时( $α > 4 5^{\circ}$ )横流向位移均方根普遍较小. 在错列角度 $α > 4 5^{\circ}$ 后,随错列角度的增大下游圆柱所受升力逐渐增大,而横流向位移均方根却逐渐减小. 这是由于本文折合速度 $U_{r}$ 的改变是通过改变柱体的刚度 $k$ 实现的. 折合速度较大时柱体的刚度较小,此时折合速度并不在锁定区间,相应单柱体的横流向振动不剧烈. 但是,错列布置方式使得下游圆柱在错列角度较小时容易受到上游圆柱尾涡的影响而在横流向产生较为剧烈的振动,使得下游圆柱横流向位移均方根在错列角度较小时普遍较大,下游圆柱的横流向振动主要由错列角度控制. 上游圆柱的横流向位移均方根随错列角度的变化规律和柱体所受升力保持一致.

从图6(c)可看出,在3个特征工况下,错列角度较小( $0^{\circ} < α # x 2264; 4 5^{\circ}$ )时,下游圆柱的顺流向振动响应都比上游圆柱剧烈;错列角度较大( $α > 4 5^{\circ}$ )时两柱体的顺流向振动响应相差较小,这与Prasanth等^[26]研究的结论一致.

3.3 涡脱频率及尾涡模态

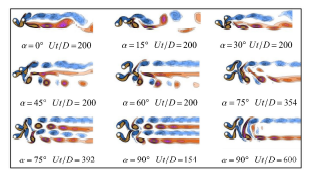
图7统计了3个特征工况中两柱体升力系数的主导频率,反映两柱体涡脱的主导频率. 图8 $~$ 图10分别是3个特征工况中不同错列角度下的瞬时流场涡量等值线,反映不同的尾涡脱落模态.

对 $U_{r} = 3.0$ ,从图8可看出错列角度较小时的“屏蔽”作用. $α = 0^{\circ}$ 和15 #x00B0;时,柱间流态呈现单钝体模式和剪切层重附着模式^[27],上游圆柱没有出现涡旋脱落. 随错列角度的增大,上游圆柱开始出现涡旋脱落,柱后涡街数量增大,涡街形态逐渐变得规则,导致图7(a)中下游圆柱涡脱的两个主导频率逐渐接近,使得柱体升力和横流向位移均方根增大,解释了上下游圆柱升力和横流向位移均方根随错列角度增大呈单调增大的现象.

显示原图| 下载原图ZIP| 生成PPT

图8 折合速度 $U r = 3.0$ 不同错列角度下尾涡模态

Fig. 8 Instantaneous vorticity contour versus different stagger angle at $U r = 3.0$

显示原图| 下载原图ZIP| 生成PPT

图9 折合速度 $U r = 5.0$ 不同错列角度下的尾涡模态

Fig. 9 Instantaneous vorticity contour versus different staggered angle at $U r = 5.0$

对 $U_{r} = 5.0$ ,从图9可看出,在 $α = 0^{\circ} ~ 3 0^{\circ}$ 时,由于上下游圆柱横流向振动都比较剧烈,两柱体在横流向的位移差使得上游圆柱在错列角度较小时也有足够的空间产生涡旋脱落,下游圆柱在整个振动周期内会穿过上游圆柱尾涡,产生较强的相互作用,这和 $U_{r} = 3.0$ 的尾涡模态不同. 在 $α = 0^{\circ}$ 时上游圆柱的尾涡交替作用在下游圆柱两侧并和符号相同的涡融合,对下游圆柱起到一个“屏蔽”作用,但这种“屏蔽”作用要比 $U_{r} = 3.0$ 上游圆柱剪切层静态附着在下游圆柱时的“屏蔽”作用弱. “屏蔽”作用随错列角度的增大而变弱,上游圆柱脱落的涡旋逐渐只能作用在下游圆柱的下侧,促进了下游圆柱的涡旋脱落,使得下游圆柱升力在 $α = 0^{\circ} ~ 3 0^{\circ}$ 的变化过程中出现了明显增大的趋势. 虽然总体上上下游圆柱的涡脱频率随错列角度的增大几乎保持不变,但是柱体的升力却呈现“上凸”的变化规律,在 $α = 3 0^{\circ}$ 处出现拐点. 从图9可看到,这是因为在 $α = 3 0^{\circ}$ 到45 #x00B0; 转变时尾涡模态从单一涡街模式转变为双涡街模式,导致升力在此产生突变. $α = 4 5^{\circ}$ 时,上下游圆柱内侧的涡旋出现“撞击”的现象. 即在整个振动周期内,上下游柱体横流向距离最小时两柱内侧涡旋会“撞击”,使得内侧将要脱落的两个涡旋“断裂”成小涡后向下游运动,小涡的脱落使得上下游圆柱升力幅值减小,导致升力减小. 同时,从 $α = 4 5^{\circ}$ 和60 #x00B0;的涡量图可以看到,这种“撞击”限制了上游圆柱的横流向振动,使得上游圆柱涡街变窄,而下游柱体的振动没有出现明显变化,尾涡脱落后形成两条平行涡街. 这也解释了图6(a)中 $α = 6 0^{\circ}$ 时上游柱体横流向位移均方根突然减小的现象. 随错列角度的继续增大( $α = 7 5^{\circ}$ 和90 #x00B0;),柱体间横流向间距变大,上述“撞击”现象所引起的抑制作用变弱,且两柱体顺流向距离的减小使得两柱尾涡出现“同相同步”和“反相同步”两种模态,导致上下游圆柱升力系数均方根、阻力系数均值及相应的位移响应逐渐相同. 值得一提的是,和 $U_{r} = 3.0$ 并列布置下的柱后尾涡相比,此时“同相同步”尾涡模态持续的时间更长. Chen等^[28]在研究并列双圆柱涡激振动时也发现了这种现象,Chen认为这是因为当两柱体横流向振幅较大时,“同相同步”状态可以使圆柱之间保持近似的距离,有效避免碰撞. 这种情况下,“同相同步”状态对两柱体的振动响应是更稳定的状态.

对 $U_{r} = 13.0$ ,从图10可看出, $α = 0^{\circ} ~ 3 0^{\circ}$ 时,两柱体横流向振幅较小,尾涡模态和 $U_{r} = 3.0$ 的尾涡模态相似. 在 $α = 3 0^{\circ}$ 和45 #x00B0; 时,刚度较小的特点使得下游圆柱在横流向的振动容易受上游圆柱尾涡脱落的影响,在横流向产生较大的位移. 下游圆柱的振动对上游圆柱尾涡产生“抑制”作用,使得上游圆柱尾涡变得“细长”. 且错列角度越大抑制作用越明显,进而导致上游圆柱在错列角度 $α = 0^{\circ} ~ 4 5^{\circ}$ 的变化过程中升力出现减小的趋势. 随着错列角度的继续增大,柱体间横向间距变大,这种影响逐渐变弱,涡街数量增大,尾涡也变得比较规则,出现了“同相同步”和“反相同步”两种模态. 如图7(c)所示, $α = 0^{\circ}$ 时,两柱体的涡脱频率都有一个次高频存在,约为单柱体涡脱频率的3倍( $f = 0.356 4$ ). 杨立红^[29]认为这是由于柱体间相互作用较强烈导致升力中的二次谐波 $(3 f)$ 的振幅较大,不可忽略. $α = 6 0^{\circ}$ 时,涡脱模态发生转变,导致两柱体升力突然增大. 横流向间距的增大使得上游圆柱发生明显的涡旋脱落,柱后涡街数量增大. 在 $α = 6 0^{\circ} ~ 9 0^{\circ}$ 的变化过程中,两柱体顺流向距离的减小和横流向间距的增加使得尾涡相互作用变弱,逐渐出现较为规则的涡街,主导频率间的差异逐渐减小. 升力系数时程曲线中“拍”的周期因主导频率差异的减小而增大,导致柱体升力系数均方根随错列角度的增大而变大. 特别的, $α = 9 0^{\circ}$ 时尾涡脱落只有“反相同步”一种模态.

显示原图| 下载原图ZIP| 生成PPT

图10 折合速度 $U r = 13.0$ 不同错列角度下尾涡模态

Fig. 10 Instantaneous vorticity contour versus different staggered angle at $U r = 13.0$

4 结论

基于自主研发的CIP方法模型对雷诺数 $Re = 100$ ,不同错列角度及不同折合速度下的双圆柱涡激振动问题进行了研究,两柱体中心间距固定为 $T = 3 D$ ,重点分析了上下游柱体的升阻力、位移响应、涡脱频率随错列角度变化的规律,并从涡脱模态变化的角度解释其原因. 主要结论如下：

(1)错列布置时,上下游圆柱是否处于锁定状态仍由折合速度决定. 不同的折合速度下,上下游柱体升阻力、振动响应、位移响应、涡脱频率及尾涡模态随错列角度的增大所呈现的规律不同,在实际工程设计中必须根据流速大小考虑较为安全的错列角度.

(2)当折合速度较小时( $U_{r} = 2.0 ~ 3.0$ ),上游圆柱尾涡对下游圆柱“屏蔽”作用较明显,柱体升阻力随错列角度的增大基本呈单调增大的趋势,且柱体升阻力的大小分别决定了柱体横流向位移均方根和顺流向位移均值的大小. 错列角度固定时,折合速度的改变对上下游柱体阻力的影响较小,对升力的影响较大.

(3)当折合速度 $U_{r} = 5.0 ~ 8.0$ 时,上下游柱体处于“锁定”状态,横流向振动较剧烈,上游圆柱尾涡对下游圆柱“屏蔽”作用较弱,随错列角度的增大上下游柱体阻力变化较小,升力呈“上凸”趋势,在 $α = 1 5^{\circ} ~ 3 0^{\circ}$ 左右取得最大值,且柱体升阻力的大小分别决定了柱体横流向位移均方根和顺流向位移均值的大小. 错列角度固定时,折合速度的改变对上下游柱体升阻力的影响都较大.

(4)当折合速度较大时( $U_{r} = 10.0 ~ 13.0$ ),上下游柱体不在“锁定”状态,但“刚度小”的特点使得下游圆柱横流向的振动在错列角度 $α = 3 0^{\circ} ~ 4 5^{\circ}$ 时容易受上游圆柱尾涡脱落的影响,在横流向产生较大的振动,“屏蔽”作用较弱. 随错列角度的增大上下游柱体阻力变化较小,升力呈“下凹”趋势,在 $α = 3 0^{\circ} ~ 4 5^{\circ}$ 左右取得最小值,且柱体横流向位移不再由升力决定. 错列角度固定时,折合速度的改变对上下游柱体升阻力的影响都较小.

(5)下游圆柱在顺流向的振动响应受错列角度的影响较大. 当 $0^{\circ} < α # x 2264; 4 5^{\circ}$ 时,下游圆柱的顺流向振动都比上游圆柱剧烈;当 $4 5^{\circ} < α # x 2264; 9 0^{\circ}$ ,上下游圆柱的顺流向振动相差较小.

The authors have declared that no competing interests exist.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]	Bearman PW. Vortex shedding from oscillating bluff bodies .Annual Review of Fluid Mechanics, 2012, 16(1): 195-222 [本文引用: 1]
[2]	Nomurt T. Finite element analysis of vortex-induced vibrations of bluff cylinder .Journal of Wind Engineering and Industrial Aerodynamics, 1993, 46: 587-594 [本文引用: 1]
[3]	及春宁,花阳,许栋等. 不同剪切率来流作用下柔性圆柱涡激振动数值模拟 .力学学报, 2018, 50(1): 21-31 [本文引用: 1] (Ji Chunning, Hua Yang, Xu Dong, et al. Numerical simulation of vortex-induced virbration of a flexible cylinder exposed to shear flow at different shear rates .Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(1): 21-31 (in Chinese)) [本文引用: 1]
[4]	高云,付世晓,熊友明等. 剪切来流下柔性圆柱体涡激振动响应试验研究 .振动与冲击, 2016, 35(20): 142-148 [本文引用: 1] (Gao Yun, Fu Shixiao, Xiong Youming, et al. Experimental study on vortex induced vibration responses of flexible cylinder in sheared current .Journal of Vibration and Shock, 2016, 35(20): 142-148 (in Chinese)) [本文引用: 1]
[5]	宋磊建,付世晓,于大鹏等. 剪切流下发生涡激振动的柔性立管阻力特性研究 .力学学报, 2016, 48(2): 300-306 [本文引用: 1] (Song Leijian, Fu Shixiao, Yu Dapeng, et al. Investigation of drag forces for flexible risers undergoing vortex-induced vibration in sheared flow .Journal of Vibration and Shock, 2016, 48(2): 300-306 (in Chinese)) [本文引用: 1]
[6]	Zhao M, Cheng L, An HW. Numerical investigation of vortex-induced virbration of circular cylinder in transverse direction in oscillatory flow .Ocean Engineering, 2012, 41(5): 39-52 [本文引用: 1]
[7]	王俊高,付世晓,许玉旺等. 正弦振荡来流下柔性立管涡激振动发展过程 .力学学报, 2014, 46(2): 173-182 [本文引用: 1] (Wang Jungao, Fu Shixiao, Xu Yuwang, et al. VIV developing process of a flexible cylinder under oscillatory flow .Chinese Journal of Theoretical and Applied Mechanics, 2014,46(2): 173-182 (in Chinese)) [本文引用: 1]
[8]	Mittal S, Kumar V, Raghuvanshi A. Unsteady incompressible flow past two cylinders in tandem and staggered arrangements .International Journal of Numerical Methods in Fluids, 1997, 25: 1315-1344 [本文引用: 1]
[9]	Prasanth TK, Mittal S. Vortex-induced vibration of two circular cylinders at low Reynolds number .Journal of Fluid and Structures, 2009, 25(4): 731-741 [本文引用: 1]
[10]	Borazjani I, Sotiropoulos F. Vortex-induced vibrations of two cylinders in tandem arrangement in the proximity-wake interference region .Journal of Fluid Mechanics, 2009, 621: 321-364 [本文引用: 1]
[11]	吴晓笛,刘华坪,陈浮. 基于浸入边界--多松弛时间格子玻尔兹曼通量求解法的流固耦合算法研究 .物理学报, 2017, 66(22): 252-265 [本文引用: 1] (Wu Xiaodi, Liu Huaping, Chen Fu. A method combined immersed boundary with multi-relaxation-time lattice Boltzmann flux solver for fluid-structure interaction .Acta Physica Sinica, 2017, 66(22): 252-265 (in Chinese)) [本文引用: 1]
[12]	郭晓玲,唐国强,刘名名等. 低雷诺数下串联双圆柱涡激振动机理的数值研究 .振动与冲击, 2014, 33(4): 60-69 [本文引用: 1] (Guo Xiaoling, Tang Guoqiang, Liu Mingming, et al. Numerical investigation on vortex-induced vibration of twin tandem circular cylinders under low Reynolds number .Journal of Vibration and Shock, 2014, 33(4): 60-69 (in Chinese)) [本文引用: 1]
[13]	Williamson CHK. Evolution of a single wake behind a pair of bluff bodies .Journal of Fluid Mechanics, 2006, 159(159): 1-18 [本文引用: 1]
[14]	Chen W, Ji C, Xu W, et al. On the responses and wake patterns of two side-by-side elastically circular cylinders in uniform laminar flow .Journal of Fluids and Structure, 2015, 55: 218-236 [本文引用: 1]
[15]	赵西增,付英男,张大可. 柱体绕流的CIP方法模拟 .哈尔滨工程大学学报, 2016, 37(3): 297-305 [本文引用: 1] (Zhao Xizeng, Fu Yingnan, Zhang Dake. Numerical simulation of flow past a cylinder using a CIP-Based model .Journal of Harbin Engineering University, 2016, 37(3): 297-305 (in Chinese)) [本文引用: 1]
[16]	Zhao X, Cheng D, Zhang D, et al. Numerical study of low-Reynolds-number flow past two tandem square cylinders with varying incident angles of the downstream one using a CIP-based model . Ocean Engineering, 2016, 121: 414-421 [本文引用: 1]
[17]	赵西增,付英男,张大可等. 紧致插值曲线方法在流向强迫振荡圆柱绕流中的应用 .力学学报, 2015, 47(3): 441-450 [本文引用: 1] (Zhao Xizeng, Fu Yingnan, Zhang Dake, et al. Application of a CIP-based numerical simulation of flow past an in-line forced oscillating circular cylinder .Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(3): 441-450 (in Chinese)) [本文引用: 1]
[18]	Yabe T, Xiao F, Utsumi T. The constrained interpolation profile method for multiphase analysis .Journal of Computational Physics, 2001, 169(2): 556-593 [本文引用: 1]
[19]	Peskin CS. Flow patterns around heart valves: a digital computer method for solving the equations of motion. [PhD Thesis] . New York: Albert Einstein College of Medicine, 1972 [本文引用: 1]
[20]	Zhao M. Flow induced vibration of two rigidly coupled circular cylinders in tandem and side-by-side arrangements at a low Reynolds number of 150 .Physics of Fluids, 2013, 25(12): 355-381 [本文引用: 1]
[21]	Meneghini JR, Saltara F, Siqueira CLR, et al. Numerical simulation of flow interference between two circular cylinders in tandem and side-by-side arrangements .Journal of Fluids and Structures, 2001, 15(2): 327-350 [本文引用: 2]
[22]	Zhou CY, So R, Lam K. Vortex-induced vibrations of an elastic circular cylinder .Journal of Fluids and Structures, 1999, 13(2): 165-189 [本文引用: 1]
[23]	Ahn HT, Kallinderis Y. Strongly coupled flow/structure interactions with a geometrically conservative ALE scheme on general hybrid meshes .Journal of Computational Physics, 2006, 219(2): 671-696
[24]	Bao Y, Zhou D, Tu J. Flow interference between a stationary cylinder and an elastically mounted cylinder arranged in proximity .Journal of Fluids and Structures, 2011, 27(8): 1425-1446
[25]	及春宁,陈威霖,黄继露等. 串列双圆柱流致振动的数值模拟及其耦合机制 .力学学报, 2014, 46(6): 862-870 [本文引用: 2] (Ji Chunning, Chen Weilin, Huang Jilu, et al. Numerical investigation on flow-induced vibration of two cylinders in tandem arrangements and its coupling mechanism .Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(6): 862-870 (in Chinese)) [本文引用: 2]
[26]	Prasanth TK, Mittal S. Vortex-induced vibration of two circular cylinders at low Reynolds number .Journal of Fluids and Structures, 2009, 25(4): 731-741 [本文引用: 1]
[27]	Zravkovich MM. The effects of flow interference between two circular cylinders in various arrangements .Journal of Fluids and Structures, 1987, 1: 239-261 [本文引用: 1]
[28]	Chen HC, Huang K, Chen CR, et al. CFD simulation of riser VIV . Final Project Report, 2006: 15-20 [本文引用: 1]
[29]	杨立红. 低雷诺数下串列多圆柱流致振动的数值模拟及其机理研究. [博士论文] .天津:天津大学, 2014 [本文引用: 1] (Yang Lihong. Numerical investigation on flow-induced vibrations of multiple circular cylinders in tandem arrangement at low Reynolds number. [PhD Thesis] . Tianjin: Tianjin University, 2014 (in Chinese)) [本文引用: 1]

Vortex shedding from oscillating bluff bodies

2012

... 涡激振动问题发生在很多实际工程中,比如海洋立管、海底管线、高耸建筑等在受到风或海流的作用时,会因涡旋脱落而导致结构振动. 和静止圆柱绕流不同,当涡旋脱落频率接近柱体自振频率时,柱体会发生“锁定” 现象^[1]. “锁定”现象的发生会使结构物发生疲劳破坏,进而缩短结构物的寿命. 双圆柱涡激振动作为多柱体涡激振动的基础,除柱体和流体本身的特性外,柱体布置方式也会影响柱体的振动响应和流场状态. 如图1所示,仅在双圆柱涡激振动中就存在3种布置方式：串列(

α = 0^{\circ}

)、并列 (

α = 9 0^{\circ}

)和错列 (

0^{\circ} < α < 9 0^{\circ}

). 其中,

α

是两柱体中心连线和来流方向之间的夹角(锐角),下文中将其简称为“错列角度”. ...

Finite element analysis of vortex-induced vibrations of bluff cylinder

1993

... 涡激振动过程涉及湍流、流动分离、涡旋拓扑、物体振动和流固耦合等复杂问题,其数值分析的难点在于动边界的处理和流场的精确捕捉. Tonmurt^[2]利用任意拉欧数值方法对雷诺数

Re = 100 ~ 140

范围的单圆柱涡激振动问题进行了系统研究,发现物体在运动时柱体表面网格的正交性不易保持,容易出现网格畸变问题. 近些年,对单圆柱涡激振动的研究集中在来流特性对振动结果的影响. 其中,剪切流对单圆柱涡激振动影响的相关研究可参考文献^[3,4,5],周期性振荡流对单圆柱涡激振动的影响可参考文献^[6,7]. 多柱体方面,Mittal等^[8]利用重叠网格技术研究了雷诺数

Re = 100

和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力

C_{d}

比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数

Re = 100

,错列角度

α \approx 7^{\circ}

双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度

7.1 < U_{r} < 8.3

时,下游圆柱运动轨迹才是“8”字型. Borazjani和Sotiropoulos^[10]利用浸入边界法处理流固耦合问题,数值模拟了串列双圆柱涡激振动问题,发现串列布置柱体的振幅和升力要比单柱体大,且在不同的折合速度下分别呈现出“2S”和“2P”两种涡旋脱落模态. 吴晓笛等^[11]基于浸入边界--多松弛时间格子波尔兹曼通量求解法的弱耦合算法对串列双圆柱双自由度涡激振动问题进行了研究. 郭晓玲等^[12]采用任意拉格朗日--欧拉动网格方法对雷诺数

Re = 150

串列双圆柱涡激振动问题进行了数值模拟. Williamson ^[13]通过模型试验对并列双圆柱涡激振动进行了研究,发现尾涡脱落存在两种方式,即同相同步. Chen等^[14]对雷诺数

Re = 100

不同间距比下并列双圆柱涡激振动进行了数值模拟,发现当间距比大于4.0时,两圆柱之间的相互作用非常弱. 可见,关于双圆柱涡激振动的研究大多是在固定两柱体的布置方式下研究不同折合速度时的柱体响应. 而实际工程中,比如,两个近距离布置的高耸烟囱、海洋立管等,在不同的来流方向下就会呈现出不同错列角度的布置方式. 如何设计常风向或者常流向下最安全的错列角度

α

是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度

U_{r}

和错列角度

0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}

下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态. ...

不同剪切率来流作用下柔性圆柱涡激振动数值模拟

2018

Re = 100 ~ 140

Re = 100

和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力

C_{d}

比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数

Re = 100

,错列角度

α \approx 7^{\circ}

双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度

7.1 < U_{r} < 8.3

Re = 150

Re = 100

α

是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度

U_{r}

和错列角度

0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}

下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态. ...

不同剪切率来流作用下柔性圆柱涡激振动数值模拟

2018

Re = 100 ~ 140

Re = 100

和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力

C_{d}

比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数

Re = 100

,错列角度

α \approx 7^{\circ}

双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度

7.1 < U_{r} < 8.3

Re = 150

Re = 100

α

是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度

U_{r}

和错列角度

0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}

下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态. ...

剪切来流下柔性圆柱体涡激振动响应试验研究

2016

Re = 100 ~ 140

Re = 100

和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力

C_{d}

比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数

Re = 100

,错列角度

α \approx 7^{\circ}

双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度

7.1 < U_{r} < 8.3

Re = 150

Re = 100

α

是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度

U_{r}

和错列角度

0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}

下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态. ...

剪切来流下柔性圆柱体涡激振动响应试验研究

2016

Re = 100 ~ 140

Re = 100

和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力

C_{d}

比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数

Re = 100

,错列角度

α \approx 7^{\circ}

双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度

7.1 < U_{r} < 8.3

Re = 150

Re = 100

α

是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度

U_{r}

和错列角度

0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}

下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态. ...

剪切流下发生涡激振动的柔性立管阻力特性研究

2016

Re = 100 ~ 140

Re = 100

和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力

C_{d}

比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数

Re = 100

,错列角度

α \approx 7^{\circ}

双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度

7.1 < U_{r} < 8.3

Re = 150

Re = 100

α

是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度

U_{r}

和错列角度

0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}

下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态. ...

剪切流下发生涡激振动的柔性立管阻力特性研究

2016

Re = 100 ~ 140

Re = 100

和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力

C_{d}

比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数

Re = 100

,错列角度

α \approx 7^{\circ}

双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度

7.1 < U_{r} < 8.3

Re = 150

Re = 100

α

是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度

U_{r}

和错列角度

0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}

下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态. ...

Numerical investigation of vortex-induced virbration of circular cylinder in transverse direction in oscillatory flow

2012

Re = 100 ~ 140

Re = 100

和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力

C_{d}

比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数

Re = 100

,错列角度

α \approx 7^{\circ}

双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度

7.1 < U_{r} < 8.3

Re = 150

Re = 100

α

是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度

U_{r}

和错列角度

0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}

下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态. ...

正弦振荡来流下柔性立管涡激振动发展过程

2014

Re = 100 ~ 140

Re = 100

和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力

C_{d}

比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数

Re = 100

,错列角度

α \approx 7^{\circ}

双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度

7.1 < U_{r} < 8.3

Re = 150

Re = 100

α

是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度

U_{r}

和错列角度

0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}

下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态. ...

正弦振荡来流下柔性立管涡激振动发展过程

2014

Re = 100 ~ 140

Re = 100

和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力

C_{d}

比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数

Re = 100

,错列角度

α \approx 7^{\circ}

双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度

7.1 < U_{r} < 8.3

Re = 150

Re = 100

α

是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度

U_{r}

和错列角度

0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}

下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态. ...

Unsteady incompressible flow past two cylinders in tandem and staggered arrangements

1997

Re = 100 ~ 140

Re = 100

和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力

C_{d}

比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数

Re = 100

,错列角度

α \approx 7^{\circ}

双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度

7.1 < U_{r} < 8.3

Re = 150

Re = 100

α

是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度

U_{r}

和错列角度

0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}

下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态. ...

Vortex-induced vibration of two circular cylinders at low Reynolds number

2009

Re = 100 ~ 140

Re = 100

和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力

C_{d}

比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数

Re = 100

,错列角度

α \approx 7^{\circ}

双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度

7.1 < U_{r} < 8.3

Re = 150

Re = 100

α

是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度

U_{r}

和错列角度

0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}

下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态. ...

Vortex-induced vibrations of two cylinders in tandem arrangement in the proximity-wake interference region

2009

Re = 100 ~ 140

Re = 100

和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力

C_{d}

比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数

Re = 100

,错列角度

α \approx 7^{\circ}

双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度

7.1 < U_{r} < 8.3

Re = 150

Re = 100

α

是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度

U_{r}

和错列角度

0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}

下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态. ...

基于浸入边界--多松弛时间格子玻尔兹曼通量求解法的流固耦合算法研究

2017

Re = 100 ~ 140

Re = 100

和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力

C_{d}

比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数

Re = 100

,错列角度

α \approx 7^{\circ}

双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度

7.1 < U_{r} < 8.3

Re = 150

Re = 100

α

是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度

U_{r}

和错列角度

0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}

下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态. ...

基于浸入边界--多松弛时间格子玻尔兹曼通量求解法的流固耦合算法研究

2017

Re = 100 ~ 140

Re = 100

和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力

C_{d}

比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数

Re = 100

,错列角度

α \approx 7^{\circ}

双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度

7.1 < U_{r} < 8.3

Re = 150

Re = 100

α

是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度

U_{r}

和错列角度

0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}

下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态. ...

低雷诺数下串联双圆柱涡激振动机理的数值研究

2014

Re = 100 ~ 140

Re = 100

和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力

C_{d}

比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数

Re = 100

,错列角度

α \approx 7^{\circ}

双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度

7.1 < U_{r} < 8.3

Re = 150

Re = 100

α

是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度

U_{r}

和错列角度

0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}

下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态. ...

低雷诺数下串联双圆柱涡激振动机理的数值研究

2014

Re = 100 ~ 140

Re = 100

和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力

C_{d}

比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数

Re = 100

,错列角度

α \approx 7^{\circ}

双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度

7.1 < U_{r} < 8.3

Re = 150

Re = 100

α

是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度

U_{r}

和错列角度

0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}

下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态. ...

Evolution of a single wake behind a pair of bluff bodies

2006

Re = 100 ~ 140

Re = 100

和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力

C_{d}

比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数

Re = 100

,错列角度

α \approx 7^{\circ}

双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度

7.1 < U_{r} < 8.3

Re = 150

Re = 100

α

是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度

U_{r}

和错列角度

0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}

下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态. ...

On the responses and wake patterns of two side-by-side elastically circular cylinders in uniform laminar flow

2015

Re = 100 ~ 140

Re = 100

和1000串列及错列布置双圆柱涡激振动问题,发现在同一雷诺数下,错列布置下游圆柱受到的阻力

C_{d}

比串列布置大. Prasanth和Mittal^[9]使用贴体动网格技术研究了雷诺数

Re = 100

,错列角度

α \approx 7^{\circ}

双圆柱涡激振动下游圆柱的运动轨迹和尾涡模态. 研究发现,只有当折合速度

7.1 < U_{r} < 8.3

Re = 150

Re = 100

α

是实际工程中必须考虑的问题. 基于此,本文拟对不同折合速度

U_{r}

和错列角度

0^{\circ} # x 2264; α # x 2264; 9 0^{\circ}

下双圆柱涡激振动进行数值模拟,系统分析柱体升阻力、位移响应和柱体后方尾涡模态. ...

柱体绕流的CIP方法模拟

2016

... 本文基于浸入边界方法的流固耦合技术,采用固定笛卡尔正交网格,在计算过程中无需更新网格,避免了重叠网格技术中的大量信息交换和任意拉欧方法中的网格畸变问题,同时可保证模型的高效率,使得模型在处理大位移的流固耦合计算中具有强大优越性. 为精确捕捉流场信息,在以前的工作中已将自主研发的紧致插值曲线方法模型应用于圆柱绕流问题^[15,16]和强迫振荡圆柱绕流问题^[17]的研究中,初步验证了该模型在处理复杂流动问题的准确性. 本文拟进一步拓展该模型的应用范围,对不同折合速度

U_{r}

和错列角度

α

下双圆柱涡激振动进行数值模拟,系统分析特定折合速度

U_{r}

下柱体升阻力、位移响应和柱体后方尾涡模态随错列角度的变化规律,以期为相关海洋工程设计提供参考数据. ...

柱体绕流的CIP方法模拟

2016

U_{r}

和错列角度

α

下双圆柱涡激振动进行数值模拟,系统分析特定折合速度

U_{r}

下柱体升阻力、位移响应和柱体后方尾涡模态随错列角度的变化规律,以期为相关海洋工程设计提供参考数据. ...

Numerical study of low-Reynolds-number flow past two tandem square cylinders with varying incident angles of the downstream one using a CIP-based model

2016

U_{r}

和错列角度

α

下双圆柱涡激振动进行数值模拟,系统分析特定折合速度

U_{r}

下柱体升阻力、位移响应和柱体后方尾涡模态随错列角度的变化规律,以期为相关海洋工程设计提供参考数据. ...

紧致插值曲线方法在流向强迫振荡圆柱绕流中的应用

2015

U_{r}

和错列角度

α

下双圆柱涡激振动进行数值模拟,系统分析特定折合速度

U_{r}

下柱体升阻力、位移响应和柱体后方尾涡模态随错列角度的变化规律,以期为相关海洋工程设计提供参考数据. ...

紧致插值曲线方法在流向强迫振荡圆柱绕流中的应用

2015

U_{r}

和错列角度

α

下双圆柱涡激振动进行数值模拟,系统分析特定折合速度

U_{r}

下柱体升阻力、位移响应和柱体后方尾涡模态随错列角度的变化规律,以期为相关海洋工程设计提供参考数据. ...

The constrained interpolation profile method for multiphase analysis

2001

... 本文所采用的CIP方法模型,核心部分在于对流体控制方程(1)和(2)进行离散,过程分为3步：(1) 采用CIP方法^[18]求解对流项;(2) 采用中心差分法求解压力项外的非对流项;(3) 采用逐次超松驰迭代(successive over relaxation,SOR)方法进行压力速度耦合. 流固耦合边界采用浸入边界法(immersed boundary method,IBM) ^[19]处理. ...

Flow patterns around heart valves: a digital computer method for solving the equations of motion. [PhD Thesis]

1972

Flow induced vibration of two rigidly coupled circular cylinders in tandem and side-by-side arrangements at a low Reynolds number of 150

2013

... 为验证网格收敛性,本节选取雷诺数

Re = 200

的单圆柱静止绕流作为算例,设置四套不同尺寸的网格 (mesh1, mesh2, mesh3, mesh4),其对应的最小网格尺寸分别为：

Δ x = Δ y = D / 50

D / 40

D / 25

和

D / 10

. 将计算出的柱体阻力系数均值

C_{d . mean}

和无量纲涡旋脱落频率

S_{t}

和文献[20,21,22]的结果进行对比,如表1所示. 可看出,mesh3和mesh4的阻力系数均值和无量纲涡旋脱落频率较其他结果偏小,mesh1和mesh2与其他文献的结果吻合较好,且mesh2的结果和文献[21]的结果相差最小. 表中RE 分别是阻力系数均值和无量纲涡脱频率相对mesh1结果的偏差. 可看出,mesh4的相对偏差较大,都在10%以上. 而mesh2结果的相对偏差都在2%以下,表明mesh2网格已具有收敛性. 综合考虑精度及计算效率,本文采用mesh2对接下来的工况进行计算. ...

Numerical simulation of flow interference between two circular cylinders in tandem and side-by-side arrangements

2001

... 为验证网格收敛性,本节选取雷诺数

Re = 200

的单圆柱静止绕流作为算例,设置四套不同尺寸的网格 (mesh1, mesh2, mesh3, mesh4),其对应的最小网格尺寸分别为：

Δ x = Δ y = D / 50

D / 40

D / 25

和

D / 10

. 将计算出的柱体阻力系数均值

C_{d . mean}

和无量纲涡旋脱落频率

S_{t}

... 所示. 可看出,mesh3和mesh4的阻力系数均值和无量纲涡旋脱落频率较其他结果偏小,mesh1和mesh2与其他文献的结果吻合较好,且mesh2的结果和文献[21]的结果相差最小. 表中RE 分别是阻力系数均值和无量纲涡脱频率相对mesh1结果的偏差. 可看出,mesh4的相对偏差较大,都在10%以上. 而mesh2结果的相对偏差都在2%以下,表明mesh2网格已具有收敛性. 综合考虑精度及计算效率,本文采用mesh2对接下来的工况进行计算. ...

Vortex-induced vibrations of an elastic circular cylinder

1999

... 为验证网格收敛性,本节选取雷诺数

Re = 200

的单圆柱静止绕流作为算例,设置四套不同尺寸的网格 (mesh1, mesh2, mesh3, mesh4),其对应的最小网格尺寸分别为：

Δ x = Δ y = D / 50

D / 40

D / 25

和

D / 10

. 将计算出的柱体阻力系数均值

C_{d . mean}

和无量纲涡旋脱落频率

S_{t}

Strongly coupled flow/structure interactions with a geometrically conservative ALE scheme on general hybrid meshes

2006

Flow interference between a stationary cylinder and an elastically mounted cylinder arranged in proximity

2011

串列双圆柱流致振动的数值模拟及其耦合机制

2014

... 本节中选取质量比

m^{*} = 2.0

,雷诺数

Re = 100

,折合速度

U_{r} = 2.0 ~ 15.0

(间隔1.0)的单圆柱涡激振动工况作为算例,并将振幅比

A^{*} = (Y_{\max} - Y_{\min}) / D

与文献[20,23-25]结果相比较,如图3. 其中,

Y_{\max}

和

Y_{\min}

分别是柱体在一个响应周期内横流向的最大、最小位移. 如图3所示,当

U_{r} = 5.0

时,振幅比

A^{*} = 0.58

,达到最大值,意味着圆柱进入频率锁定状态,与及春宁等^[25]的结果吻合较好. 随折合速度的增大,振幅比逐渐变小,在

U_{r} = 9.0

时,振幅比

A^{*} = 0.117 8

,远小于锁定区间的振幅比,柱体脱离频率锁定区. 通过对比可看出,柱体振幅比随折合速度变化的规律和现有文献结果吻合较好. ...

... 从图4和图5可看出,除了过渡区的折合速度 (

U_{r} = 4.0

和9.0)外,其他折合速度下柱体升阻力随错列角度的变化规律在同一区域内具有相似性. 对于

U_{r} = 2.0 ~ 3.0

,如图4(a)所示,

α = 0^{\circ}

时下游圆柱阻力几乎为零,说明上游圆柱尾流对下游圆柱的“屏蔽”作用^[25]较强,即下游圆柱处在上游圆柱的尾流中,来流速度较小导致下游圆柱阻力较小. ...

串列双圆柱流致振动的数值模拟及其耦合机制

2014

... 本节中选取质量比

m^{*} = 2.0

,雷诺数

Re = 100

,折合速度

U_{r} = 2.0 ~ 15.0

(间隔1.0)的单圆柱涡激振动工况作为算例,并将振幅比

A^{*} = (Y_{\max} - Y_{\min}) / D

与文献[20,23-25]结果相比较,如图3. 其中,

Y_{\max}

和

Y_{\min}

分别是柱体在一个响应周期内横流向的最大、最小位移. 如图3所示,当

U_{r} = 5.0

时,振幅比

A^{*} = 0.58

,达到最大值,意味着圆柱进入频率锁定状态,与及春宁等^[25]的结果吻合较好. 随折合速度的增大,振幅比逐渐变小,在

U_{r} = 9.0

时,振幅比

A^{*} = 0.117 8

,远小于锁定区间的振幅比,柱体脱离频率锁定区. 通过对比可看出,柱体振幅比随折合速度变化的规律和现有文献结果吻合较好. ...

... 从图4和图5可看出,除了过渡区的折合速度 (

U_{r} = 4.0

和9.0)外,其他折合速度下柱体升阻力随错列角度的变化规律在同一区域内具有相似性. 对于

U_{r} = 2.0 ~ 3.0

,如图4(a)所示,

α = 0^{\circ}

Vortex-induced vibration of two circular cylinders at low Reynolds number

2009

... 从图6(c)可看出,在3个特征工况下,错列角度较小(

0^{\circ} < α # x 2264; 4 5^{\circ}

)时,下游圆柱的顺流向振动响应都比上游圆柱剧烈;错列角度较大(

α > 4 5^{\circ}

)时两柱体的顺流向振动响应相差较小,这与Prasanth等^[26]研究的结论一致. ...

The effects of flow interference between two circular cylinders in various arrangements

1987

... 对

U_{r} = 3.0

,从图8可看出错列角度较小时的“屏蔽”作用.

α = 0^{\circ}

和15 #x00B0;时,柱间流态呈现单钝体模式和剪切层重附着模式^[27],上游圆柱没有出现涡旋脱落. 随错列角度的增大,上游圆柱开始出现涡旋脱落,柱后涡街数量增大,涡街形态逐渐变得规则,导致图7(a)中下游圆柱涡脱的两个主导频率逐渐接近,使得柱体升力和横流向位移均方根增大,解释了上下游圆柱升力和横流向位移均方根随错列角度增大呈单调增大的现象. ...

CFD simulation of riser VIV

2006

... 对

U_{r} = 5.0

,从图9可看出,在

α = 0^{\circ} ~ 3 0^{\circ}

时,由于上下游圆柱横流向振动都比较剧烈,两柱体在横流向的位移差使得上游圆柱在错列角度较小时也有足够的空间产生涡旋脱落,下游圆柱在整个振动周期内会穿过上游圆柱尾涡,产生较强的相互作用,这和

U_{r} = 3.0

的尾涡模态不同. 在

α = 0^{\circ}

时上游圆柱的尾涡交替作用在下游圆柱两侧并和符号相同的涡融合,对下游圆柱起到一个“屏蔽”作用,但这种“屏蔽”作用要比

U_{r} = 3.0

上游圆柱剪切层静态附着在下游圆柱时的“屏蔽”作用弱. “屏蔽”作用随错列角度的增大而变弱,上游圆柱脱落的涡旋逐渐只能作用在下游圆柱的下侧,促进了下游圆柱的涡旋脱落,使得下游圆柱升力在

α = 0^{\circ} ~ 3 0^{\circ}

的变化过程中出现了明显增大的趋势. 虽然总体上上下游圆柱的涡脱频率随错列角度的增大几乎保持不变,但是柱体的升力却呈现“上凸”的变化规律,在

α = 3 0^{\circ}

处出现拐点. 从图9可看到,这是因为在

α = 3 0^{\circ}

到45 #x00B0; 转变时尾涡模态从单一涡街模式转变为双涡街模式,导致升力在此产生突变.

α = 4 5^{\circ}

时,上下游圆柱内侧的涡旋出现“撞击”的现象. 即在整个振动周期内,上下游柱体横流向距离最小时两柱内侧涡旋会“撞击”,使得内侧将要脱落的两个涡旋“断裂”成小涡后向下游运动,小涡的脱落使得上下游圆柱升力幅值减小,导致升力减小. 同时,从

α = 4 5^{\circ}

和60 #x00B0;的涡量图可以看到,这种“撞击”限制了上游圆柱的横流向振动,使得上游圆柱涡街变窄,而下游柱体的振动没有出现明显变化,尾涡脱落后形成两条平行涡街. 这也解释了图6(a)中

α = 6 0^{\circ}

时上游柱体横流向位移均方根突然减小的现象. 随错列角度的继续增大(

α = 7 5^{\circ}

和90 #x00B0;),柱体间横流向间距变大,上述“撞击”现象所引起的抑制作用变弱,且两柱体顺流向距离的减小使得两柱尾涡出现“同相同步”和“反相同步”两种模态,导致上下游圆柱升力系数均方根、阻力系数均值及相应的位移响应逐渐相同. 值得一提的是,和

U_{r} = 3.0

并列布置下的柱后尾涡相比,此时“同相同步”尾涡模态持续的时间更长. Chen等^[28]在研究并列双圆柱涡激振动时也发现了这种现象,Chen认为这是因为当两柱体横流向振幅较大时,“同相同步”状态可以使圆柱之间保持近似的距离,有效避免碰撞. 这种情况下,“同相同步”状态对两柱体的振动响应是更稳定的状态. ...

低雷诺数下串列多圆柱流致振动的数值模拟及其机理研究. [博士论文]

2014

... 对

U_{r} = 13.0

,从图10可看出,

α = 0^{\circ} ~ 3 0^{\circ}

时,两柱体横流向振幅较小,尾涡模态和

U_{r} = 3.0

的尾涡模态相似. 在

α = 3 0^{\circ}

和45 #x00B0; 时,刚度较小的特点使得下游圆柱在横流向的振动容易受上游圆柱尾涡脱落的影响,在横流向产生较大的位移. 下游圆柱的振动对上游圆柱尾涡产生“抑制”作用,使得上游圆柱尾涡变得“细长”. 且错列角度越大抑制作用越明显,进而导致上游圆柱在错列角度

α = 0^{\circ} ~ 4 5^{\circ}

的变化过程中升力出现减小的趋势. 随着错列角度的继续增大,柱体间横向间距变大,这种影响逐渐变弱,涡街数量增大,尾涡也变得比较规则,出现了“同相同步”和“反相同步”两种模态. 如图7(c)所示,

α = 0^{\circ}

时,两柱体的涡脱频率都有一个次高频存在,约为单柱体涡脱频率的3倍(

f = 0.356 4

). 杨立红^[29]认为这是由于柱体间相互作用较强烈导致升力中的二次谐波

(3 f)

的振幅较大,不可忽略.

α = 6 0^{\circ}

时,涡脱模态发生转变,导致两柱体升力突然增大. 横流向间距的增大使得上游圆柱发生明显的涡旋脱落,柱后涡街数量增大. 在

α = 6 0^{\circ} ~ 9 0^{\circ}

的变化过程中,两柱体顺流向距离的减小和横流向间距的增加使得尾涡相互作用变弱,逐渐出现较为规则的涡街,主导频率间的差异逐渐减小. 升力系数时程曲线中“拍”的周期因主导频率差异的减小而增大,导致柱体升力系数均方根随错列角度的增大而变大. 特别的,

α = 9 0^{\circ}

时尾涡脱落只有“反相同步”一种模态. ...

低雷诺数下串列多圆柱流致振动的数值模拟及其机理研究. [博士论文]

2014

... 对

U_{r} = 13.0

,从图10可看出,

α = 0^{\circ} ~ 3 0^{\circ}

时,两柱体横流向振幅较小,尾涡模态和

U_{r} = 3.0

的尾涡模态相似. 在

α = 3 0^{\circ}

α = 0^{\circ} ~ 4 5^{\circ}

α = 0^{\circ}

时,两柱体的涡脱频率都有一个次高频存在,约为单柱体涡脱频率的3倍(

f = 0.356 4

). 杨立红^[29]认为这是由于柱体间相互作用较强烈导致升力中的二次谐波

(3 f)

的振幅较大,不可忽略.

α = 6 0^{\circ}

时,涡脱模态发生转变,导致两柱体升力突然增大. 横流向间距的增大使得上游圆柱发生明显的涡旋脱落,柱后涡街数量增大. 在

α = 6 0^{\circ} ~ 9 0^{\circ}

α = 9 0^{\circ}

时尾涡脱落只有“反相同步”一种模态. ...

〈

〉

错列角度对双圆柱涡激振动影响的数值模拟研究

NUMERICAL STUDY OF STAGGERED ANGLE ON THE VORTEX-INDUCED VIBRATION OF TWO CYLINDERS

引言

1 数值方法

2 模型验证

2.1 网格收敛性验证

2.2 单圆柱涡激振动

3 结果与讨论

3.1 柱体升阻力系数

3.2 柱体振动响应、位移响应

3.3 涡脱频率及尾涡模态

4 结论

参考文献 文献选项 原文顺序 文献年度倒序 文中引用次数倒序 被引期刊影响因子

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子