引言
柱体结构(包括圆柱、方柱等)广泛应用于海洋工程领域,比如Spar平台、张力腿平台和半潜式平台等[1 ] . 当一定速度的流体流经柱体结构物时,由于黏性的存在,会发生边界层分离,形成漩涡,周期性的漩涡脱落导致脉动压力,进而诱发结构物大幅度振动,这可能会破坏海洋平台系泊和立管系统[2 ] . 柱体间的耦合干扰导致多柱式平台表现出与单柱式平台不同的涡激运动特性[3 ] . 因此,柱体绕流的研究具有重要的应用价值.
目前,柱体绕流研究方法主要包括实验和计算流体力学(computational fluid dynamics, CFD)数值模拟. 国内外学者已对柱体绕流做了大量实验研究[4 ,5 ,6 ,7 ] . 相比于实验研究,CFD数值模拟方法成本低、速度快. 近年来,随着计算机技术的不断发展,CFD数值模拟方法更加受到重视. Travin等[8 ] 运用分离涡(detached-eddy simulation, DES)方法数值模拟了不同雷诺数下单圆柱绕流的情况,验证了DES方法数值模拟圆柱绕流的可行性. 及春宁等[9 ] 采用浸入边界法研究了细长柔性圆柱在线性剪切流下的涡激振动特性. 吴应湘等[10 ] 通过模型实验和数值模拟方法,研究了带有涡激振动抑制罩的圆柱体的水动力特性. Sohankar [11 ] 采用大涡模拟(large eddy simulation,LES)方法研究了 1.0 × 1 0 3 < Re < 5.0 × 1 0 6 Re > 2.0 × 1 0 4 [12 ] 运用LES方法对 Re = 2.2 × 1 0 4 L ) 与直径( D ) 的比值小于3.25时,只有下游圆柱有涡脱落现象,而当 L / D > 3.25 L c / D = 3.25 L / D > L c / D [13 ] 利用RNG k -- ε Re = 2.2 × 1 0 4
然而,在上述研究中,针对高雷诺数下的串列双圆柱绕流和串列双方柱绕流的研究均较少, 而在实际海洋工程应用中,雷诺数往往在105 以上. 基于此,本文采用改进的延迟分离涡(improve delayed detached-eddy simulation, IDDES)方法数值模拟 2.0 × 1 0 3 < Re < 3.0 × 1 0 6
1 数值模型
1.1 改进的延迟分离涡(IDDES)方法
分离涡[14 ] 方法(也称为DES97方法)是一种结合了雷诺平均方法(Reynolds-averaged Navier-Stokes, RANS)与LES方法的混合方法,已被证实是一种有效的数值方法. DES方法在近壁面使用RANS方法进行模拟,而在远离壁面的分离区使用LES方法模拟来捕捉大尺度分离流动.
DES97方法对长度尺度 l DES l DES = min d , C des Δ (1) 其中, d Δ = max Δ x , Δ y , Δ z Δ x Δ y Δ z C des
从式(1)可以看出DES97方法中,RANS到LES的转换完全取决于网格尺度大小. 在某些情况下会导致RANS提前转换到LES,出现模型应力耗散(modeled stress depletion, MSD)现象,从而导致“网格诱导分离(grid-induced separation, GID)”问题. 同时DES97方法还存在“对数层不匹配(log-layer mismatch, LLM)”问题.
Spalart等[15 ] 提出延迟分离涡(delayed detached-eddy simulation, DDES)方法来解决GID问题. DDES方法对长度尺度 l DDES l DDES = d - f d max 0 , d - C des Δ (2) 式中, f d f d
IDDES方法则是将DDES方法与WMLES (wall-modelling LES)方法相结合,从而解决了LLM问题,同时提高了近壁面湍流的求解质量[16 ] .
1.2 计算域及网格划分
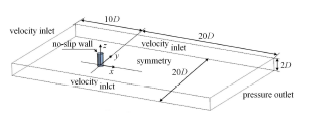
单圆柱计算域及边界条件的设定如图1 所示,入口距离圆柱中心为 10 D ( D 20 D 10 D 2 D 30 D × 20 D × 2 D D
图1 单圆柱计算域及边界条件
Fig. 1 Computational domain and boundary conditions for a circular cylinder
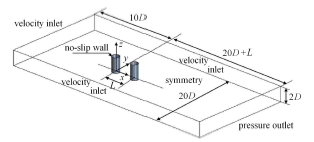
串列双圆柱计算域及边界条件的设定如图2 所示,入口距离上游圆柱中心为10 D L D D D . 间距比 L / D L D L / D 30 D × 20 D + L × 2 D D L
图2 双圆柱计算域及边界条件
Fig. 2 Computational domain and boundary conditions for two tandem circular cylinders
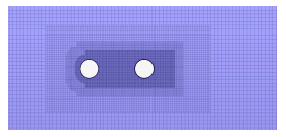
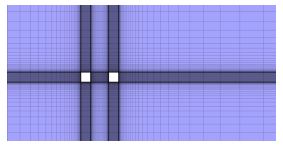
双圆柱及双方柱网格划分如图3 和图4 所示(以 L = 3 D y +
图3 双圆柱网格划分示意图
Fig. 3 Grid distribution of two tandem circular cylinders
图4 双方柱网格划分示意图
Fig. 4 Grid distribution of two tandem square cylinders
2 计算结果与分析
2.1 网格收敛性分析及数值模型验证
网格的疏密程度不仅会影响计算精度,还会影响计算效率. 网格收敛性分析以 Re = 3.0 × 1 0 6 Δ t = tU / D t U D 表1 所示.
表1 给出了3套网格下计算的平均阻力系数 C d ¯ C ' l St C d ¯ C ' l St
针对圆柱绕流工况,本文所模拟的雷诺数区域包括亚临界雷诺数区域和超临界雷诺数区域,前面网格收敛性分析已经对 Re = 3.0 × 1 0 6 ( 超临界雷诺数区域)进行验证,因此针对圆柱绕流再选取 Re = 2.2 × 1 0 4 ( 亚临界雷诺数区域)进行验证,其中 Re = 2.2 × 1 0 4 Re = 3.0 × 1 0 6 表2 所示.
从表2 中可以看出本文计算的平均阻力系数 C d ¯ St C ' l
对于单方柱绕流选取 Re = 2.2 × 1 0 4 表3 所示.
3 Re = 2.2 × 1 0 4
从表3 可以看出,本文计算的 C d ¯ C ' l St
总体上讲,上述结果很好地验证了本文所采用的IDDES方法在模拟圆柱绕流及方柱绕流的有效性和准确性.
2.2 单圆柱绕流及单方柱绕流
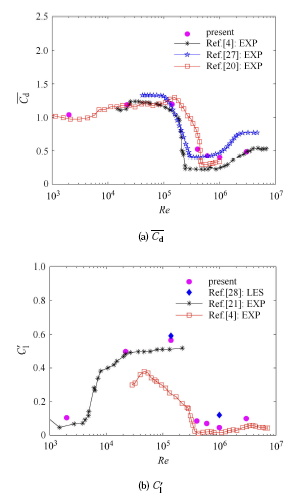
单圆柱绕流的平均阻力系数 C d ¯ C ' l St 图5 所示. 从图5 (a)中可以看出本文的计算结果与实验结果吻合良好,随着雷诺数的增大,单圆柱绕流的 C d ¯ 图5 (b)可以看出本文计算的 C ' l
图5 不同雷诺数下单圆柱绕流的平均阻力系数、升力系数均方根和斯特劳哈尔数
Fig. 5 Mean drag coefficient, RMS lift coefficient and Strouhal number of a circular cylinder versus Re
图5(续) 不同雷诺数下单圆柱绕流的平均阻力系数、升力系数均方根和斯特劳哈尔数(续)
Fig. 5(continued) Mean drag coefficient, RMS lift coefficient and Strouhal number of a circular cylinder versus Re
实验值偏大,但与文献[28 ]的计算结果接近, C ' l 图5 (c)中可以看出,本文计算的 St 3.0 × 1 0 5 < Re < 1.0 × 1 0 6
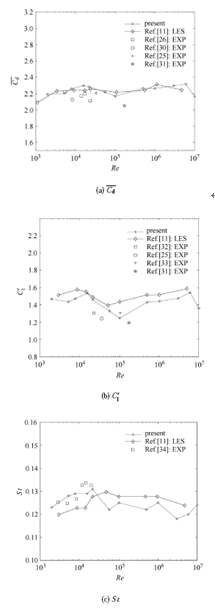
图6 为单方柱绕流的平均阻力系数 C d ¯ C ' l St 图6 (a)可以看出,本文计算的 C ' l ¯ 图6 (b)看出本文计算的 C ' l 11 ]的计算结果,更接近于实验数据,随雷诺数的增大, C ' l 图6 (c)可以看出本文计算的 St St ~ 0.13 范围内.
图6 不同雷诺数下单放柱绕流的平均阻力系数、升力系数均方根和斯特劳哈尔数
Fig. 6 Mean drag coefficient, RMS lift coefficient and Strouhal number of a square cylinder versus Re
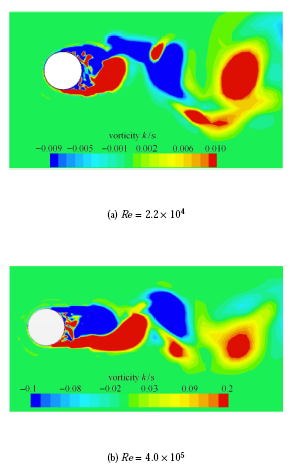
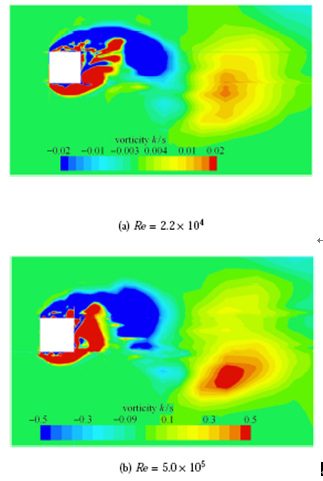
在 2.0 × 1 0 3 < Re < 1.0 × 1 0 7 C d ¯ C ' l St [11 ] 用LES方法数值模拟了较高雷诺数(最高达106 量级)下的方柱绕流,其研究同样表明方柱绕流未出现阻力危机现象. 图7 为 Re = 2.2 × 1 0 4 Re = 4.0 × 1 0 5 图7 可以看出, Re = 4.0 × 1 0 5 图8 为 Re = 2.2 × 1 0 4 Re = 5.0 × 1 0 5 图8 可以看出,方柱绕流的分离点固定,压差阻力无明显变化,因此单方柱绕流未出现阻力危机现象.
图7 不同雷诺数下,单圆柱绕流的瞬时涡量图
Fig. 7 Instantaneous vorticity distributions for flow past a circular cylinder at different Reynolds numbers
图8 不同雷诺数下,单方柱绕流的瞬时涡量图
Fig. 8 Instantaneous vorticity distributions for flow past a square circular cylinder at different Reynolds numbers
2.3 串列双圆柱绕流及串列双方柱绕流
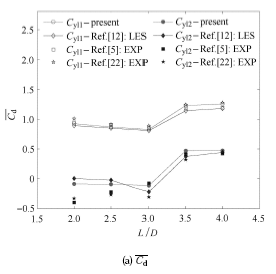
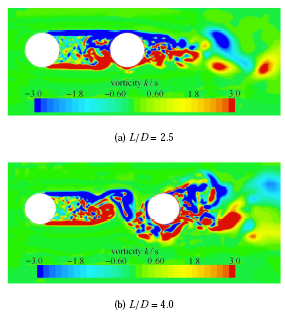
图9 为雷诺数 Re = 2.2 × 1 0 4 L / D ) 下串列双圆柱绕流的平均阻力系数 C d ¯ C ' l C yl 1 C yl 2 C d ¯ 图9 (b)中可以看出,本文计算的 C ' l Re = 2.2 × 1 0 4 3.0 < L / D < 3.5 L c / D ) 使得串列双圆柱绕流的 C d ¯ C ' l 图10 所示,当 L = 2.5 D ( 即 L / D < L c / D ) 时,前柱后方还没有单独涡脱落,而当 L = 4.0 D ( 即 L / D > L c / D ) 时,前柱后方已经有单独的涡脱落现象,正是由于这种流态的变化才使得 C d ¯ C ' l L / D < L c / D L / D > L c / D
图9 Re=2.2×104 时,不同间距比下串列双圆绕流的${\rm{\bar C}}$d 和C' l
Fig. 9 Mean drag coefficient and RMS lift coefficient of upstream and downstream circular cylinders for different spacing to diameter ratios (L/D) at Re=2.2×104
图9(续) Re=2.2×104 时,不同间距比下串列双圆绕流的${\rm{\bar C}}$d 和C' l (续)
Fig. 9(continued) Mean drag coefficient and RMS lift coefficient of upstream and downstream circular cylinders for different spacing to diameter ratios (L/D) at Re=2.2×104 (continued)
图10 Re=2.2×104 时,圆柱中心高度处不同间距比下的瞬时涡量图
Fig. 10 Instantaneous vorticity distributions of circular cylinders at middle of cylinder span in the case of different spacing to diameter ratios at Re=2.2×104
图11 为 Re = 2.2 × 1 0 4 Re = 3.0 × 1 0 6 C d ¯ C ' l Re = 3.0 × 1 0 6 Re = 2.2 × 1 0 4 Re = 3.0 × 1 0 6 ) ,串列双圆柱绕流不再存在临界间距比,随着间距比的增大,下游圆柱的阻力系数和升力系数均缓慢增大,而上游圆柱的阻力系数和升力系数则趋于稳定,均无出现明显的跳跃性变化,而且下游圆柱的阻力系数始终为正数. 对比图10 (b)与图12 (b)可以看出,对于 Re = 3.0 × 1 0 6 L / D = 4.0
图11 不同雷诺数时,不同间距比下串列双圆柱绕流的${\rm{\bar C}}$d 和C' l
Fig.11 Mean drag coefficient and RMS lift coefficient of upstream and downstream circular cylinders for different spacing to diameter ratios (L/D) at different Re
图12 Re = 3.0 × 1 0 6
Fig. 12 Instantaneous vorticity distributions of circular cylinders at middle of cylinder span in the case of different spacing to diameter ratios at Re = 3.0 × 1 0 6
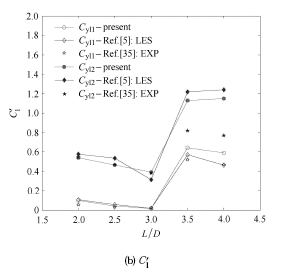
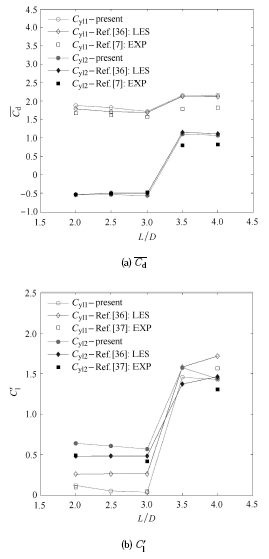
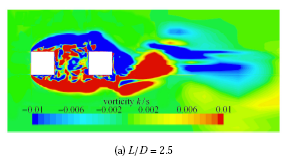
图13 为雷诺数 Re = 1.6 × 1 0 4 C d ¯ C ' l C yl 1 C yl 2 C d ¯ C d ¯ 图13 (b)中可以看出,本文计算的上游方柱 C ' l C ' l Re = 1.6 × 1 0 4 3.0 < L / D < 3.5 L c / D ) 使得串列双方柱绕流的 C d ¯ C ' l 图14 所示,上下游方柱水动力系数发生跳跃性变化也是由于流态发生变化而导致的. 只有在 L / D > L c / D L / D < L c / D L / D > L c / D
图13 Re=1.6×104 时,不同间距比下串列双方柱绕流的${\rm{\bar C}}$d 和C' l
Fig. 13 Mean drag coefficient and RMS lift coefficient of upstream and downstream square cylinders for different spacing to diameter ratios at Re=1.6×104
图14 Re = 1.6 × 1 0 4
Fig. 14 Instantaneous vorticity distributions of square cylinders at middle of cylinder span in the case of different spacing to diameter ratios at Re = 1.6 × 1 0 4
图14(续) Re=1.6×104 时,方柱中心高度处不同间距比下的瞬时涡量图(续)
Fig. 14(continued) Instantaneous vorticity distributions of square cylinders at middle of cylinder span in the case of different spacing to diameter ratios at Re=1.6×104 (continued)
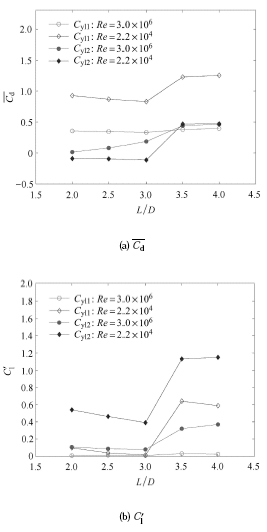
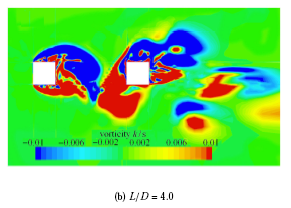
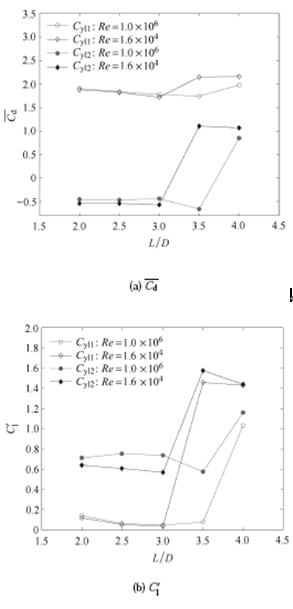
图15 为 Re = 1.6 × 1 0 4 Re = 1.0 × 1 0 6 d 和C' l 随间距比的变化情况. 从图中可以看出,与串列双圆柱绕流情况不同,串列双方柱绕流在两种雷诺数下均存在一临界间距比Lc /D,当 L / D > L c / D Re = 1.6 × 1 0 4 L c / D 3.0 < L / D < 3.5 Re = 1.0 × 1 0 6 L c / D 3.5 < L / D < 4.0 图16 (b)所示,上游方柱后方形成的漩涡的位置与图14 (b)类似,均很靠近上游方柱,因此 Re = 1.0 × 1 0 6 L / D < L c / D
图15 不同雷诺数时,不同间距比下串列双方柱绕流的${\rm{\bar C}}$d 和C' l
Fig. 15 Mean drag coefficient and RMS lift coefficient of upstream and downstream square cylinders for different spacing to diameter ratios at different Re
图16 Re = 1.0 × 1 0 6
Fig. 16 Instantaneous vorticity distributions of square cylinders at middle of cylinder span in the case of different spacing to diameter ratios at Re = 1.0 × 1 0 6
3 结论
本文采用改进的延迟分离涡方法数值模拟了较高下的圆柱绕流及方柱绕流,研究了不同雷诺数下圆柱绕流与方柱绕流的水动力特性,本文的计算结果与已有的实验数据以及其他文献的CFD计算结果吻合良好,验证了本文所采用的IDDES方法在数值模拟柱体绕流时的准确性和有效性. 通过结果的对比分析,可以得到以下结论:
(1)在 2.0 × 1 0 3 < Re < 1.0 × 1 0 7 C d ¯ C ' l St
(2)串列双圆柱绕流中,当 Re = 2.2 × 1 0 4 3.0 < L c / D < 3.5 ) 使得 L c / D Re = 3.0 × 1 0 6
(3)串列双方柱绕流中,在 Re = 1.6 × 1 0 4 Re = 1.0 × 1 0 6 L / D > L c / D L c / D
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
周振威 ,孙树民 . 深海海洋平台发展综述
. 广东造船 ,2012 ,31 (3 ):63 -66
[本文引用: 1]
(Zhou Zhenwei Sun Shumin Review on the development of deep water ofshore platform
.Guangdong Shipbuilding , 2012 , 31 (3 ):63 -66 (in Chinese))
[本文引用: 1]
[2]
张新曙 ,尤云祥 ,滕明清 . 深海半潜浮式生产平台关键理论与技术问题
. 海洋工程 ,2016 ,34 (1 ):117 -123
[本文引用: 1]
(Zhang Xinshu You Yunxiang Teng Mingqing Review of the key theories and technologies for the development of deep-sea semi-submersible floating production unit
.The Ocean Engineering , 2016 , 34 (1 ):117 -123 (in Chinese))
[本文引用: 1]
[3]
张新曙 ,胡晓峰 ,尤云祥 等 . 深海多立柱浮式平台涡激运动特性研究
. 力学学报 ,2016 ,48 (3 ):593 -598
[本文引用: 1]
(Zhang Xinshu Hu Xiaofeng You Yunxiang et al .Investigation on the characterisitics of vortex induced motion of a deep sea multi-column floating platform
.Chinese Journal of Theoretical and Applied Mechanics , 2016 , 48 (3 ):593 -598 (in Chinese))
[本文引用: 1]
[4]
Schewe G On the force fluctuations acting on a circular cylinder in crossflow from subcritical up to transcritical Reynolds numbers
.J Fluid Mech , 1983 , 133 : 265 -285
[本文引用: 2]
[5]
Ljungkrona L Norberg CH Sunden B Free-stream turbulence and tube spacing effects on surface pressure fluctuations for two tubes in an in-line arrangement
.J Fluids Struct , 1991 , 5 (6 ): 701 -727
[本文引用: 1]
[6]
Lyn DA Einav S Rodi W et al .A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder
.J Fluid Mech , 1995 , 304 : 285 -319
[本文引用: 2]
[7]
Liu CH Chen JM Observations of hysteresis in flow around two square cylinders in a tandem arrangement
.J Wind Eng Ind Aerodyn , 2002 , 90 (9 ): 1019 -1050
[本文引用: 1]
[8]
Travin A Shur M Strelets M et al .Detached-Eddy Simulations Past a Circular Cylinder
.Flow, Turb Comb , 2000 , 63 (1-4 ): 293 -313
[本文引用: 2]
[9]
及春宁 ,花阳 ,许栋 等 . 不同剪切率来流作用下柔性圆柱涡激振动数值模拟
. 力学学报 ,2018 , 50 (1 ): 21 -31
[本文引用: 1]
(Ji Chunning Hua Yang Xu Dong et al .Numerical simulation of vortex-induced vibration of a flexible cylinder exposed to shear flow at different shear rates
.Chinese Journal of Theoretical and Applied Mechanics , 2018 , 50 (1 ): 21 -31 (in Chinese))
[本文引用: 1]
[10]
吴应湘 ,林黎明 ,钟兴福 . 带有新型涡激振动抑制罩的圆柱体的水动力特性
. 力学学报 ,2016 ,48 (2 ):307 -317
[本文引用: 1]
(Zhang Xinshu Hu Xiaofeng You Yunxiang et al .Investigation in hydrodynamics of a circular cylinder with the new suppressing shroud for vortex-induced vibration
.Chinese Journal of Theoretical and Applied Mechanics , 2016 , 48 (2 ): 307 -317 (in Chinese))
[本文引用: 1]
[11]
Sohankar A Flow over a bluff body from moderate to high Reynolds numbers using large eddy simulation
. J Computers & Fluids , 2006 , 35 (10 ): 1154 -1168
[本文引用: 3]
[12]
Kitagawaa T Ohtab H Numerical investigation on flow around circular cylinders in tandem arrangement at a subcritical Reynolds number
.J Fluids Struct , 2008 , 24 (5 ): 680 -699
[本文引用: 1]
[13]
吕启兵 , 杨斌 , 杨忠超 等 . 串列双方柱绕流的数值模拟
. 重庆交通大学学报:自然科学版 ,2013 ,32 (5 ): 1010 -1013
[本文引用: 1]
(Lü Qibing Yang Bin Yang Zhongchao et al .Numerical simulation of flow around two square cylinders in tandem arrangement
.Journal of Chongqing Jiaotong University ( Natural Science )2013 , 32 (5 ): 1010 -1013 (in Chinese))
[本文引用: 1]
[14]
Spalart PR Jou WH Strelets M et al. Comments on the Feasibility of LES for wings , and on a hybrid RANS/LES approach//Proceedings of First AFOSR International Conference on DNS/LES Approach Ruston, Louisiana, 1997-8-4-8. Greyden Press , 1997 . 137
[本文引用: 1]
[15]
Spalart PR Deck S Shur ML et al .A new version of detached-eddy simulation, resistant to ambiguous grid densities
.Theoret Comput Fluid Dyn , 2006 , 20 (30 ): 181 -195
[本文引用: 1]
[16]
Shur ML Spalart PR Strelets MK et al .A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities
.Int J Heat Fluid Flow , 2008 , 29 (6 ): 1638 -1649
[本文引用: 1]
[17]
Lo SC Hoffmann KA Dietiker JF Numerical investigation of high reynolds number flows over square and circular cylinders
.J Thermophys Heat Transfer , 2005 , 19 (1 ): 72 -80
[本文引用: 2]
[18]
Ong MC Utnes T Holmedal LE et al .Numerical simulation of flow around a smooth circular cylinder at very high Reynolds numbers
.Marine Structures , 2009 , 22 (2 ): 142 -153
[本文引用: 1]
[19]
Jones GW Cincotta JJ Walker RW Aerodynamic forces on a stationary and oscillating circular cylinder at high Reynolds numbers
. NASA Technical Report , 1969 , 17 -30
[本文引用: 1]
[20]
Wieselsberger C Versuche über den Luftwiderstand gerundeter und kantiger Körper//Prandtl L. ed. Ergebnisse Aerodyn
. Versuchsanstalt Göttingen , 1923 . 23
[21]
Norberg C Fluctuating lift on a circular cylinder: review and new measurements
.J Fluids Struct , 2003 , 17 (1 ): 57 -96
[22]
Igarashi T Characteristics of the flow around two circular cylinders arranged in tandem: 1st Report
.JSME Int J , 1981 , 24 (188 ): 323 -331
[23]
Trias FX Gorobets A Oliva A Turbulent flow around a square cylinder at Reynolds number 22,000: A DNS study
.J Computers & Fluids , 2015 , 123 : 87 -98
[本文引用: 1]
[24]
Sohankar A Davidson L Norberg C Large eddy simulation of flow past a square cylinder: comparison of different subgrid scale models
.J Fluids Eng , 2000 , 122 (1 ): 39 -47
[本文引用: 1]
[25]
Luo SC Yazdani MG Chew YT et al .Effects of incidence and afterbody shape on flow past bluff cylinders
.J Wind EngInd Aerodyn , 1994 , 53 : 375 -399
[本文引用: 1]
[26]
Norberg C Flow around rectangular cylinders: Pressure forces and wake frequencies
.J Wind EngInd Aerodyn , 1993 , 49 (1-3 ): 187 -196
[本文引用: 1]
[27]
Achenbach E Influence of surface roughness on the cross-flow around a circular cylinder
.J Fluid Mech , 1971 , 46 (2 ): 321 -335
[28]
Kim SE Mohan LS. Prediction of unsteady loading on a circular cylinder in high reynolds number flows using large eddy simulation//Proceedings of OMAE 2005 : 24th International Conference on Offshore Mechanics and Arctic Engineering, Halkidiki, Greece, 2005-6-12-
16 , 775 -783
[本文引用: 1]
[29]
Vaz G Mabilat C Wal RVD et al . Viscous flow computations on a smooth cylinders: a detailed numerical study with validation//Proceedings of OMAE2007 : 26th International Conference on Offshore Mechanics and Arctic Engineering, San Diego, California, USA 2007-6-10-
15 , 849 -860
[30]
Saha AK Muralidhar K Biswas G Experimental study of flow past a square cylinder at high Reynolds numbers
.Exper Fluids , 2000 , 29 (6 ): 553 -563
[31]
Lee BE The effect of turbulence on the surface pressure field of a square prism
.J Fluid Mech , 1975 , 69 (2 ): 263 -282
[32]
McLean I Gartshore C Spanwise correlations of pressure on a rigid square section cylinder
.J Wind Engng Ind Aero , 1992 , 41 (92 ): 797 -808
[33]
Vickery BJ Fluctuating lift and drag on a long cylinder of square cross-section in a smooth and in a turbulent stream
.J Fluid Mech , 1966 , 25 (3 ): 481 -494
[34]
Okajima A Strouhal number of rectangular cylinder
.J Fluid Mech , 1982 , 123 (-1 ): 379 -398
[35]
Alam MM Moriya M Takai K et al .Fluctuating fluid forces acting on two circular cylinders in a tandem arrangement at a subcritical Reynolds number
.J Wind Engng Ind Aero , 2003 , 91 (1 ): 139 -154
[36]
Sohankar A A LES study of the flow interference between tandem square cylinder pairs
.Theor Comput Fluid Dyn , 2014 , 28 (5 ): 531 -548
[37]
Alam MMD Moriya M Takai K et al .Suppression of fluid forces acting on two square prisms in a tandem arrangement by passive control of flow
.J Fluids Struct , 2002 , 16 (8 ): 1073 -1092
深海海洋平台发展综述
1
2012
... 柱体结构(包括圆柱、方柱等)广泛应用于海洋工程领域,比如Spar平台、张力腿平台和半潜式平台等[1 ] . 当一定速度的流体流经柱体结构物时,由于黏性的存在,会发生边界层分离,形成漩涡,周期性的漩涡脱落导致脉动压力,进而诱发结构物大幅度振动,这可能会破坏海洋平台系泊和立管系统[2 ] . 柱体间的耦合干扰导致多柱式平台表现出与单柱式平台不同的涡激运动特性[3 ] . 因此,柱体绕流的研究具有重要的应用价值. ...
深海海洋平台发展综述
1
2012
... 柱体结构(包括圆柱、方柱等)广泛应用于海洋工程领域,比如Spar平台、张力腿平台和半潜式平台等[1 ] . 当一定速度的流体流经柱体结构物时,由于黏性的存在,会发生边界层分离,形成漩涡,周期性的漩涡脱落导致脉动压力,进而诱发结构物大幅度振动,这可能会破坏海洋平台系泊和立管系统[2 ] . 柱体间的耦合干扰导致多柱式平台表现出与单柱式平台不同的涡激运动特性[3 ] . 因此,柱体绕流的研究具有重要的应用价值. ...
深海半潜浮式生产平台关键理论与技术问题
1
2016
... 柱体结构(包括圆柱、方柱等)广泛应用于海洋工程领域,比如Spar平台、张力腿平台和半潜式平台等[1 ] . 当一定速度的流体流经柱体结构物时,由于黏性的存在,会发生边界层分离,形成漩涡,周期性的漩涡脱落导致脉动压力,进而诱发结构物大幅度振动,这可能会破坏海洋平台系泊和立管系统[2 ] . 柱体间的耦合干扰导致多柱式平台表现出与单柱式平台不同的涡激运动特性[3 ] . 因此,柱体绕流的研究具有重要的应用价值. ...
深海半潜浮式生产平台关键理论与技术问题
1
2016
... 柱体结构(包括圆柱、方柱等)广泛应用于海洋工程领域,比如Spar平台、张力腿平台和半潜式平台等[1 ] . 当一定速度的流体流经柱体结构物时,由于黏性的存在,会发生边界层分离,形成漩涡,周期性的漩涡脱落导致脉动压力,进而诱发结构物大幅度振动,这可能会破坏海洋平台系泊和立管系统[2 ] . 柱体间的耦合干扰导致多柱式平台表现出与单柱式平台不同的涡激运动特性[3 ] . 因此,柱体绕流的研究具有重要的应用价值. ...
深海多立柱浮式平台涡激运动特性研究
1
2016
... 柱体结构(包括圆柱、方柱等)广泛应用于海洋工程领域,比如Spar平台、张力腿平台和半潜式平台等[1 ] . 当一定速度的流体流经柱体结构物时,由于黏性的存在,会发生边界层分离,形成漩涡,周期性的漩涡脱落导致脉动压力,进而诱发结构物大幅度振动,这可能会破坏海洋平台系泊和立管系统[2 ] . 柱体间的耦合干扰导致多柱式平台表现出与单柱式平台不同的涡激运动特性[3 ] . 因此,柱体绕流的研究具有重要的应用价值. ...
深海多立柱浮式平台涡激运动特性研究
1
2016
... 柱体结构(包括圆柱、方柱等)广泛应用于海洋工程领域,比如Spar平台、张力腿平台和半潜式平台等[1 ] . 当一定速度的流体流经柱体结构物时,由于黏性的存在,会发生边界层分离,形成漩涡,周期性的漩涡脱落导致脉动压力,进而诱发结构物大幅度振动,这可能会破坏海洋平台系泊和立管系统[2 ] . 柱体间的耦合干扰导致多柱式平台表现出与单柱式平台不同的涡激运动特性[3 ] . 因此,柱体绕流的研究具有重要的应用价值. ...
On the force fluctuations acting on a circular cylinder in crossflow from subcritical up to transcritical Reynolds numbers
2
1983
... 目前,柱体绕流研究方法主要包括实验和计算流体力学(computational fluid dynamics, CFD)数值模拟. 国内外学者已对柱体绕流做了大量实验研究[4 ,5 ,6 ,7 ] . 相比于实验研究,CFD数值模拟方法成本低、速度快. 近年来,随着计算机技术的不断发展,CFD数值模拟方法更加受到重视. Travin等[8 ] 运用分离涡(detached-eddy simulation, DES)方法数值模拟了不同雷诺数下单圆柱绕流的情况,验证了DES方法数值模拟圆柱绕流的可行性. 及春宁等[9 ] 采用浸入边界法研究了细长柔性圆柱在线性剪切流下的涡激振动特性. 吴应湘等[10 ] 通过模型实验和数值模拟方法,研究了带有涡激振动抑制罩的圆柱体的水动力特性. Sohankar [11 ] 采用大涡模拟(large eddy simulation,LES)方法研究了 1.0 × 1 0 3 < Re < 5.0 × 1 0 6 Re > 2.0 × 1 0 4 [12 ] 运用LES方法对 Re = 2.2 × 1 0 4 L ) 与直径( D ) 的比值小于3.25时,只有下游圆柱有涡脱落现象,而当 L / D > 3.25 L c / D = 3.25 L / D > L c / D [13 ] 利用RNG k -- ε Re = 2.2 × 1 0 4
... Sensitivity of the results to different grids
Case Grids C d ¯ C ' l St G1 543 500 0.472 0.067 0.262 G2 797 300 0.484 0.099 0.307 G3 1 160 700 0.486 0.102 0.309 CFD [8 ,17 -18 ] — 0.457~ 0.535 0.077~ 0.100 0.305~ 0.330 EXP [4 ,19 ] — 0.460~ 0.540 0.060~ 0.100 0.210~ 0.214
针对圆柱绕流工况,本文所模拟的雷诺数区域包括亚临界雷诺数区域和超临界雷诺数区域,前面网格收敛性分析已经对 Re = 3.0 × 1 0 6 ( 超临界雷诺数区域)进行验证,因此针对圆柱绕流再选取 Re = 2.2 × 1 0 4 ( 亚临界雷诺数区域)进行验证,其中 Re = 2.2 × 1 0 4 Re = 3.0 × 1 0 6 表2 所示. ...
Free-stream turbulence and tube spacing effects on surface pressure fluctuations for two tubes in an in-line arrangement
1
1991
... 目前,柱体绕流研究方法主要包括实验和计算流体力学(computational fluid dynamics, CFD)数值模拟. 国内外学者已对柱体绕流做了大量实验研究[4 ,5 ,6 ,7 ] . 相比于实验研究,CFD数值模拟方法成本低、速度快. 近年来,随着计算机技术的不断发展,CFD数值模拟方法更加受到重视. Travin等[8 ] 运用分离涡(detached-eddy simulation, DES)方法数值模拟了不同雷诺数下单圆柱绕流的情况,验证了DES方法数值模拟圆柱绕流的可行性. 及春宁等[9 ] 采用浸入边界法研究了细长柔性圆柱在线性剪切流下的涡激振动特性. 吴应湘等[10 ] 通过模型实验和数值模拟方法,研究了带有涡激振动抑制罩的圆柱体的水动力特性. Sohankar [11 ] 采用大涡模拟(large eddy simulation,LES)方法研究了 1.0 × 1 0 3 < Re < 5.0 × 1 0 6 Re > 2.0 × 1 0 4 [12 ] 运用LES方法对 Re = 2.2 × 1 0 4 L ) 与直径( D ) 的比值小于3.25时,只有下游圆柱有涡脱落现象,而当 L / D > 3.25 L c / D = 3.25 L / D > L c / D [13 ] 利用RNG k -- ε Re = 2.2 × 1 0 4
A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder
2
1995
... 目前,柱体绕流研究方法主要包括实验和计算流体力学(computational fluid dynamics, CFD)数值模拟. 国内外学者已对柱体绕流做了大量实验研究[4 ,5 ,6 ,7 ] . 相比于实验研究,CFD数值模拟方法成本低、速度快. 近年来,随着计算机技术的不断发展,CFD数值模拟方法更加受到重视. Travin等[8 ] 运用分离涡(detached-eddy simulation, DES)方法数值模拟了不同雷诺数下单圆柱绕流的情况,验证了DES方法数值模拟圆柱绕流的可行性. 及春宁等[9 ] 采用浸入边界法研究了细长柔性圆柱在线性剪切流下的涡激振动特性. 吴应湘等[10 ] 通过模型实验和数值模拟方法,研究了带有涡激振动抑制罩的圆柱体的水动力特性. Sohankar [11 ] 采用大涡模拟(large eddy simulation,LES)方法研究了 1.0 × 1 0 3 < Re < 5.0 × 1 0 6 Re > 2.0 × 1 0 4 [12 ] 运用LES方法对 Re = 2.2 × 1 0 4 L ) 与直径( D ) 的比值小于3.25时,只有下游圆柱有涡脱落现象,而当 L / D > 3.25 L c / D = 3.25 L / D > L c / D [13 ] 利用RNG k -- ε Re = 2.2 × 1 0 4
... Comparison of results of a square cylinder (
Re = 2.2 × 1 0 4 ) C d ¯ C ' l St Present 2.280 1.459 0.131 CFD [17 ,23 -24 ] 2.180~ 2.320 1.540~ 1.710 0.132 EXP [6 ,25 -26 ] 2.100~ 2.210 1.210 0.130
从表3 可以看出,本文计算的 C d ¯ C ' l St
Observations of hysteresis in flow around two square cylinders in a tandem arrangement
1
2002
... 目前,柱体绕流研究方法主要包括实验和计算流体力学(computational fluid dynamics, CFD)数值模拟. 国内外学者已对柱体绕流做了大量实验研究[4 ,5 ,6 ,7 ] . 相比于实验研究,CFD数值模拟方法成本低、速度快. 近年来,随着计算机技术的不断发展,CFD数值模拟方法更加受到重视. Travin等[8 ] 运用分离涡(detached-eddy simulation, DES)方法数值模拟了不同雷诺数下单圆柱绕流的情况,验证了DES方法数值模拟圆柱绕流的可行性. 及春宁等[9 ] 采用浸入边界法研究了细长柔性圆柱在线性剪切流下的涡激振动特性. 吴应湘等[10 ] 通过模型实验和数值模拟方法,研究了带有涡激振动抑制罩的圆柱体的水动力特性. Sohankar [11 ] 采用大涡模拟(large eddy simulation,LES)方法研究了 1.0 × 1 0 3 < Re < 5.0 × 1 0 6 Re > 2.0 × 1 0 4 [12 ] 运用LES方法对 Re = 2.2 × 1 0 4 L ) 与直径( D ) 的比值小于3.25时,只有下游圆柱有涡脱落现象,而当 L / D > 3.25 L c / D = 3.25 L / D > L c / D [13 ] 利用RNG k -- ε Re = 2.2 × 1 0 4
Detached-Eddy Simulations Past a Circular Cylinder
2
2000
... 目前,柱体绕流研究方法主要包括实验和计算流体力学(computational fluid dynamics, CFD)数值模拟. 国内外学者已对柱体绕流做了大量实验研究[4 ,5 ,6 ,7 ] . 相比于实验研究,CFD数值模拟方法成本低、速度快. 近年来,随着计算机技术的不断发展,CFD数值模拟方法更加受到重视. Travin等[8 ] 运用分离涡(detached-eddy simulation, DES)方法数值模拟了不同雷诺数下单圆柱绕流的情况,验证了DES方法数值模拟圆柱绕流的可行性. 及春宁等[9 ] 采用浸入边界法研究了细长柔性圆柱在线性剪切流下的涡激振动特性. 吴应湘等[10 ] 通过模型实验和数值模拟方法,研究了带有涡激振动抑制罩的圆柱体的水动力特性. Sohankar [11 ] 采用大涡模拟(large eddy simulation,LES)方法研究了 1.0 × 1 0 3 < Re < 5.0 × 1 0 6 Re > 2.0 × 1 0 4 [12 ] 运用LES方法对 Re = 2.2 × 1 0 4 L ) 与直径( D ) 的比值小于3.25时,只有下游圆柱有涡脱落现象,而当 L / D > 3.25 L c / D = 3.25 L / D > L c / D [13 ] 利用RNG k -- ε Re = 2.2 × 1 0 4
... Sensitivity of the results to different grids
Case Grids C d ¯ C ' l St G1 543 500 0.472 0.067 0.262 G2 797 300 0.484 0.099 0.307 G3 1 160 700 0.486 0.102 0.309 CFD [8 ,17 -18 ] — 0.457~ 0.535 0.077~ 0.100 0.305~ 0.330 EXP [4 ,19 ] — 0.460~ 0.540 0.060~ 0.100 0.210~ 0.214
针对圆柱绕流工况,本文所模拟的雷诺数区域包括亚临界雷诺数区域和超临界雷诺数区域,前面网格收敛性分析已经对 Re = 3.0 × 1 0 6 ( 超临界雷诺数区域)进行验证,因此针对圆柱绕流再选取 Re = 2.2 × 1 0 4 ( 亚临界雷诺数区域)进行验证,其中 Re = 2.2 × 1 0 4 Re = 3.0 × 1 0 6 表2 所示. ...
不同剪切率来流作用下柔性圆柱涡激振动数值模拟
1
2018
... 目前,柱体绕流研究方法主要包括实验和计算流体力学(computational fluid dynamics, CFD)数值模拟. 国内外学者已对柱体绕流做了大量实验研究[4 ,5 ,6 ,7 ] . 相比于实验研究,CFD数值模拟方法成本低、速度快. 近年来,随着计算机技术的不断发展,CFD数值模拟方法更加受到重视. Travin等[8 ] 运用分离涡(detached-eddy simulation, DES)方法数值模拟了不同雷诺数下单圆柱绕流的情况,验证了DES方法数值模拟圆柱绕流的可行性. 及春宁等[9 ] 采用浸入边界法研究了细长柔性圆柱在线性剪切流下的涡激振动特性. 吴应湘等[10 ] 通过模型实验和数值模拟方法,研究了带有涡激振动抑制罩的圆柱体的水动力特性. Sohankar [11 ] 采用大涡模拟(large eddy simulation,LES)方法研究了 1.0 × 1 0 3 < Re < 5.0 × 1 0 6 Re > 2.0 × 1 0 4 [12 ] 运用LES方法对 Re = 2.2 × 1 0 4 L ) 与直径( D ) 的比值小于3.25时,只有下游圆柱有涡脱落现象,而当 L / D > 3.25 L c / D = 3.25 L / D > L c / D [13 ] 利用RNG k -- ε Re = 2.2 × 1 0 4
不同剪切率来流作用下柔性圆柱涡激振动数值模拟
1
2018
... 目前,柱体绕流研究方法主要包括实验和计算流体力学(computational fluid dynamics, CFD)数值模拟. 国内外学者已对柱体绕流做了大量实验研究[4 ,5 ,6 ,7 ] . 相比于实验研究,CFD数值模拟方法成本低、速度快. 近年来,随着计算机技术的不断发展,CFD数值模拟方法更加受到重视. Travin等[8 ] 运用分离涡(detached-eddy simulation, DES)方法数值模拟了不同雷诺数下单圆柱绕流的情况,验证了DES方法数值模拟圆柱绕流的可行性. 及春宁等[9 ] 采用浸入边界法研究了细长柔性圆柱在线性剪切流下的涡激振动特性. 吴应湘等[10 ] 通过模型实验和数值模拟方法,研究了带有涡激振动抑制罩的圆柱体的水动力特性. Sohankar [11 ] 采用大涡模拟(large eddy simulation,LES)方法研究了 1.0 × 1 0 3 < Re < 5.0 × 1 0 6 Re > 2.0 × 1 0 4 [12 ] 运用LES方法对 Re = 2.2 × 1 0 4 L ) 与直径( D ) 的比值小于3.25时,只有下游圆柱有涡脱落现象,而当 L / D > 3.25 L c / D = 3.25 L / D > L c / D [13 ] 利用RNG k -- ε Re = 2.2 × 1 0 4
带有新型涡激振动抑制罩的圆柱体的水动力特性
1
2016
... 目前,柱体绕流研究方法主要包括实验和计算流体力学(computational fluid dynamics, CFD)数值模拟. 国内外学者已对柱体绕流做了大量实验研究[4 ,5 ,6 ,7 ] . 相比于实验研究,CFD数值模拟方法成本低、速度快. 近年来,随着计算机技术的不断发展,CFD数值模拟方法更加受到重视. Travin等[8 ] 运用分离涡(detached-eddy simulation, DES)方法数值模拟了不同雷诺数下单圆柱绕流的情况,验证了DES方法数值模拟圆柱绕流的可行性. 及春宁等[9 ] 采用浸入边界法研究了细长柔性圆柱在线性剪切流下的涡激振动特性. 吴应湘等[10 ] 通过模型实验和数值模拟方法,研究了带有涡激振动抑制罩的圆柱体的水动力特性. Sohankar [11 ] 采用大涡模拟(large eddy simulation,LES)方法研究了 1.0 × 1 0 3 < Re < 5.0 × 1 0 6 Re > 2.0 × 1 0 4 [12 ] 运用LES方法对 Re = 2.2 × 1 0 4 L ) 与直径( D ) 的比值小于3.25时,只有下游圆柱有涡脱落现象,而当 L / D > 3.25 L c / D = 3.25 L / D > L c / D [13 ] 利用RNG k -- ε Re = 2.2 × 1 0 4
带有新型涡激振动抑制罩的圆柱体的水动力特性
1
2016
... 目前,柱体绕流研究方法主要包括实验和计算流体力学(computational fluid dynamics, CFD)数值模拟. 国内外学者已对柱体绕流做了大量实验研究[4 ,5 ,6 ,7 ] . 相比于实验研究,CFD数值模拟方法成本低、速度快. 近年来,随着计算机技术的不断发展,CFD数值模拟方法更加受到重视. Travin等[8 ] 运用分离涡(detached-eddy simulation, DES)方法数值模拟了不同雷诺数下单圆柱绕流的情况,验证了DES方法数值模拟圆柱绕流的可行性. 及春宁等[9 ] 采用浸入边界法研究了细长柔性圆柱在线性剪切流下的涡激振动特性. 吴应湘等[10 ] 通过模型实验和数值模拟方法,研究了带有涡激振动抑制罩的圆柱体的水动力特性. Sohankar [11 ] 采用大涡模拟(large eddy simulation,LES)方法研究了 1.0 × 1 0 3 < Re < 5.0 × 1 0 6 Re > 2.0 × 1 0 4 [12 ] 运用LES方法对 Re = 2.2 × 1 0 4 L ) 与直径( D ) 的比值小于3.25时,只有下游圆柱有涡脱落现象,而当 L / D > 3.25 L c / D = 3.25 L / D > L c / D [13 ] 利用RNG k -- ε Re = 2.2 × 1 0 4
Flow over a bluff body from moderate to high Reynolds numbers using large eddy simulation
3
2006
... 目前,柱体绕流研究方法主要包括实验和计算流体力学(computational fluid dynamics, CFD)数值模拟. 国内外学者已对柱体绕流做了大量实验研究[4 ,5 ,6 ,7 ] . 相比于实验研究,CFD数值模拟方法成本低、速度快. 近年来,随着计算机技术的不断发展,CFD数值模拟方法更加受到重视. Travin等[8 ] 运用分离涡(detached-eddy simulation, DES)方法数值模拟了不同雷诺数下单圆柱绕流的情况,验证了DES方法数值模拟圆柱绕流的可行性. 及春宁等[9 ] 采用浸入边界法研究了细长柔性圆柱在线性剪切流下的涡激振动特性. 吴应湘等[10 ] 通过模型实验和数值模拟方法,研究了带有涡激振动抑制罩的圆柱体的水动力特性. Sohankar [11 ] 采用大涡模拟(large eddy simulation,LES)方法研究了 1.0 × 1 0 3 < Re < 5.0 × 1 0 6 Re > 2.0 × 1 0 4 [12 ] 运用LES方法对 Re = 2.2 × 1 0 4 L ) 与直径( D ) 的比值小于3.25时,只有下游圆柱有涡脱落现象,而当 L / D > 3.25 L c / D = 3.25 L / D > L c / D [13 ] 利用RNG k -- ε Re = 2.2 × 1 0 4
... 图6 为单方柱绕流的平均阻力系数 C d ¯ C ' l St 图6 (a)可以看出,本文计算的 C ' l ¯ 图6 (b)看出本文计算的 C ' l 11 ]的计算结果,更接近于实验数据,随雷诺数的增大, C ' l 图6 (c)可以看出本文计算的 St St ~ 0.13 范围内. ...
... 在 2.0 × 1 0 3 < Re < 1.0 × 1 0 7 C d ¯ C ' l St [11 ] 用LES方法数值模拟了较高雷诺数(最高达106 量级)下的方柱绕流,其研究同样表明方柱绕流未出现阻力危机现象. 图7 为 Re = 2.2 × 1 0 4 Re = 4.0 × 1 0 5 图7 可以看出, Re = 4.0 × 1 0 5 图8 为 Re = 2.2 × 1 0 4 Re = 5.0 × 1 0 5 图8 可以看出,方柱绕流的分离点固定,压差阻力无明显变化,因此单方柱绕流未出现阻力危机现象. ...
Numerical investigation on flow around circular cylinders in tandem arrangement at a subcritical Reynolds number
1
2008
... 目前,柱体绕流研究方法主要包括实验和计算流体力学(computational fluid dynamics, CFD)数值模拟. 国内外学者已对柱体绕流做了大量实验研究[4 ,5 ,6 ,7 ] . 相比于实验研究,CFD数值模拟方法成本低、速度快. 近年来,随着计算机技术的不断发展,CFD数值模拟方法更加受到重视. Travin等[8 ] 运用分离涡(detached-eddy simulation, DES)方法数值模拟了不同雷诺数下单圆柱绕流的情况,验证了DES方法数值模拟圆柱绕流的可行性. 及春宁等[9 ] 采用浸入边界法研究了细长柔性圆柱在线性剪切流下的涡激振动特性. 吴应湘等[10 ] 通过模型实验和数值模拟方法,研究了带有涡激振动抑制罩的圆柱体的水动力特性. Sohankar [11 ] 采用大涡模拟(large eddy simulation,LES)方法研究了 1.0 × 1 0 3 < Re < 5.0 × 1 0 6 Re > 2.0 × 1 0 4 [12 ] 运用LES方法对 Re = 2.2 × 1 0 4 L ) 与直径( D ) 的比值小于3.25时,只有下游圆柱有涡脱落现象,而当 L / D > 3.25 L c / D = 3.25 L / D > L c / D [13 ] 利用RNG k -- ε Re = 2.2 × 1 0 4
串列双方柱绕流的数值模拟
1
2013
... 目前,柱体绕流研究方法主要包括实验和计算流体力学(computational fluid dynamics, CFD)数值模拟. 国内外学者已对柱体绕流做了大量实验研究[4 ,5 ,6 ,7 ] . 相比于实验研究,CFD数值模拟方法成本低、速度快. 近年来,随着计算机技术的不断发展,CFD数值模拟方法更加受到重视. Travin等[8 ] 运用分离涡(detached-eddy simulation, DES)方法数值模拟了不同雷诺数下单圆柱绕流的情况,验证了DES方法数值模拟圆柱绕流的可行性. 及春宁等[9 ] 采用浸入边界法研究了细长柔性圆柱在线性剪切流下的涡激振动特性. 吴应湘等[10 ] 通过模型实验和数值模拟方法,研究了带有涡激振动抑制罩的圆柱体的水动力特性. Sohankar [11 ] 采用大涡模拟(large eddy simulation,LES)方法研究了 1.0 × 1 0 3 < Re < 5.0 × 1 0 6 Re > 2.0 × 1 0 4 [12 ] 运用LES方法对 Re = 2.2 × 1 0 4 L ) 与直径( D ) 的比值小于3.25时,只有下游圆柱有涡脱落现象,而当 L / D > 3.25 L c / D = 3.25 L / D > L c / D [13 ] 利用RNG k -- ε Re = 2.2 × 1 0 4
串列双方柱绕流的数值模拟
1
2013
... 目前,柱体绕流研究方法主要包括实验和计算流体力学(computational fluid dynamics, CFD)数值模拟. 国内外学者已对柱体绕流做了大量实验研究[4 ,5 ,6 ,7 ] . 相比于实验研究,CFD数值模拟方法成本低、速度快. 近年来,随着计算机技术的不断发展,CFD数值模拟方法更加受到重视. Travin等[8 ] 运用分离涡(detached-eddy simulation, DES)方法数值模拟了不同雷诺数下单圆柱绕流的情况,验证了DES方法数值模拟圆柱绕流的可行性. 及春宁等[9 ] 采用浸入边界法研究了细长柔性圆柱在线性剪切流下的涡激振动特性. 吴应湘等[10 ] 通过模型实验和数值模拟方法,研究了带有涡激振动抑制罩的圆柱体的水动力特性. Sohankar [11 ] 采用大涡模拟(large eddy simulation,LES)方法研究了 1.0 × 1 0 3 < Re < 5.0 × 1 0 6 Re > 2.0 × 1 0 4 [12 ] 运用LES方法对 Re = 2.2 × 1 0 4 L ) 与直径( D ) 的比值小于3.25时,只有下游圆柱有涡脱落现象,而当 L / D > 3.25 L c / D = 3.25 L / D > L c / D [13 ] 利用RNG k -- ε Re = 2.2 × 1 0 4
1
1997
... 分离涡[14 ] 方法(也称为DES97方法)是一种结合了雷诺平均方法(Reynolds-averaged Navier-Stokes, RANS)与LES方法的混合方法,已被证实是一种有效的数值方法. DES方法在近壁面使用RANS方法进行模拟,而在远离壁面的分离区使用LES方法模拟来捕捉大尺度分离流动. ...
A new version of detached-eddy simulation, resistant to ambiguous grid densities
1
2006
... Spalart等[15 ] 提出延迟分离涡(delayed detached-eddy simulation, DDES)方法来解决GID问题. DDES方法对长度尺度 l DDES l DDES = d - f d max 0 , d - C des Δ (2) 式中, f d f d
A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities
1
2008
... IDDES方法则是将DDES方法与WMLES (wall-modelling LES)方法相结合,从而解决了LLM问题,同时提高了近壁面湍流的求解质量[16 ] . ...
Numerical investigation of high reynolds number flows over square and circular cylinders
2
2005
... Sensitivity of the results to different grids
Case Grids C d ¯ C ' l St G1 543 500 0.472 0.067 0.262 G2 797 300 0.484 0.099 0.307 G3 1 160 700 0.486 0.102 0.309 CFD [8 ,17 -18 ] — 0.457~ 0.535 0.077~ 0.100 0.305~ 0.330 EXP [4 ,19 ] — 0.460~ 0.540 0.060~ 0.100 0.210~ 0.214
针对圆柱绕流工况,本文所模拟的雷诺数区域包括亚临界雷诺数区域和超临界雷诺数区域,前面网格收敛性分析已经对 Re = 3.0 × 1 0 6 ( 超临界雷诺数区域)进行验证,因此针对圆柱绕流再选取 Re = 2.2 × 1 0 4 ( 亚临界雷诺数区域)进行验证,其中 Re = 2.2 × 1 0 4 Re = 3.0 × 1 0 6 表2 所示. ...
... Comparison of results of a square cylinder (
Re = 2.2 × 1 0 4 ) C d ¯ C ' l St Present 2.280 1.459 0.131 CFD [17 ,23 -24 ] 2.180~ 2.320 1.540~ 1.710 0.132 EXP [6 ,25 -26 ] 2.100~ 2.210 1.210 0.130
从表3 可以看出,本文计算的 C d ¯ C ' l St
Numerical simulation of flow around a smooth circular cylinder at very high Reynolds numbers
1
2009
... Sensitivity of the results to different grids
Case Grids C d ¯ C ' l St G1 543 500 0.472 0.067 0.262 G2 797 300 0.484 0.099 0.307 G3 1 160 700 0.486 0.102 0.309 CFD [8 ,17 -18 ] — 0.457~ 0.535 0.077~ 0.100 0.305~ 0.330 EXP [4 ,19 ] — 0.460~ 0.540 0.060~ 0.100 0.210~ 0.214
针对圆柱绕流工况,本文所模拟的雷诺数区域包括亚临界雷诺数区域和超临界雷诺数区域,前面网格收敛性分析已经对 Re = 3.0 × 1 0 6 ( 超临界雷诺数区域)进行验证,因此针对圆柱绕流再选取 Re = 2.2 × 1 0 4 ( 亚临界雷诺数区域)进行验证,其中 Re = 2.2 × 1 0 4 Re = 3.0 × 1 0 6 表2 所示. ...
Aerodynamic forces on a stationary and oscillating circular cylinder at high Reynolds numbers
1
1969
... Sensitivity of the results to different grids
Case Grids C d ¯ C ' l St G1 543 500 0.472 0.067 0.262 G2 797 300 0.484 0.099 0.307 G3 1 160 700 0.486 0.102 0.309 CFD [8 ,17 -18 ] — 0.457~ 0.535 0.077~ 0.100 0.305~ 0.330 EXP [4 ,19 ] — 0.460~ 0.540 0.060~ 0.100 0.210~ 0.214
针对圆柱绕流工况,本文所模拟的雷诺数区域包括亚临界雷诺数区域和超临界雷诺数区域,前面网格收敛性分析已经对 Re = 3.0 × 1 0 6 ( 超临界雷诺数区域)进行验证,因此针对圆柱绕流再选取 Re = 2.2 × 1 0 4 ( 亚临界雷诺数区域)进行验证,其中 Re = 2.2 × 1 0 4 Re = 3.0 × 1 0 6 表2 所示. ...
Versuche über den Luftwiderstand gerundeter und kantiger Körper//Prandtl L. ed. Ergebnisse Aerodyn
1923
Fluctuating lift on a circular cylinder: review and new measurements
2003
Characteristics of the flow around two circular cylinders arranged in tandem: 1st Report
1981
Turbulent flow around a square cylinder at Reynolds number 22,000: A DNS study
1
2015
... Comparison of results of a square cylinder (
Re = 2.2 × 1 0 4 ) C d ¯ C ' l St Present 2.280 1.459 0.131 CFD [17 ,23 -24 ] 2.180~ 2.320 1.540~ 1.710 0.132 EXP [6 ,25 -26 ] 2.100~ 2.210 1.210 0.130
从表3 可以看出,本文计算的 C d ¯ C ' l St
Large eddy simulation of flow past a square cylinder: comparison of different subgrid scale models
1
2000
... Comparison of results of a square cylinder (
Re = 2.2 × 1 0 4 ) C d ¯ C ' l St Present 2.280 1.459 0.131 CFD [17 ,23 -24 ] 2.180~ 2.320 1.540~ 1.710 0.132 EXP [6 ,25 -26 ] 2.100~ 2.210 1.210 0.130
从表3 可以看出,本文计算的 C d ¯ C ' l St
Effects of incidence and afterbody shape on flow past bluff cylinders
1
1994
... Comparison of results of a square cylinder (
Re = 2.2 × 1 0 4 ) C d ¯ C ' l St Present 2.280 1.459 0.131 CFD [17 ,23 -24 ] 2.180~ 2.320 1.540~ 1.710 0.132 EXP [6 ,25 -26 ] 2.100~ 2.210 1.210 0.130
从表3 可以看出,本文计算的 C d ¯ C ' l St
Flow around rectangular cylinders: Pressure forces and wake frequencies
1
1993
... Comparison of results of a square cylinder (
Re = 2.2 × 1 0 4 ) C d ¯ C ' l St Present 2.280 1.459 0.131 CFD [17 ,23 -24 ] 2.180~ 2.320 1.540~ 1.710 0.132 EXP [6 ,25 -26 ] 2.100~ 2.210 1.210 0.130
从表3 可以看出,本文计算的 C d ¯ C ' l St
Influence of surface roughness on the cross-flow around a circular cylinder
1971
24th International Conference on Offshore Mechanics and Arctic Engineering, Halkidiki, Greece, 2005-6-12-
1
2005
... 实验值偏大,但与文献[28 ]的计算结果接近, C ' l 图5 (c)中可以看出,本文计算的 St 3.0 × 1 0 5 < Re < 1.0 × 1 0 6
26th International Conference on Offshore Mechanics and Arctic Engineering, San Diego, California, USA 2007-6-10-
2007
Experimental study of flow past a square cylinder at high Reynolds numbers
2000
The effect of turbulence on the surface pressure field of a square prism
1975
Spanwise correlations of pressure on a rigid square section cylinder
1992
Fluctuating lift and drag on a long cylinder of square cross-section in a smooth and in a turbulent stream
1966
Strouhal number of rectangular cylinder
1982
Fluctuating fluid forces acting on two circular cylinders in a tandem arrangement at a subcritical Reynolds number
2003
A LES study of the flow interference between tandem square cylinder pairs
2014
Suppression of fluid forces acting on two square prisms in a tandem arrangement by passive control of flow
2002