力学学报 2018 , 50 (2): 221-232 https://doi.org/10.6052/0459-1879-17-242

流体力学

激波主导流动下壁板的热气动弹性稳定性理论分析

叶柳青²⁾^,, 叶正寅

西北工业大学航空学院,西安 710072

AEROELASTIC STABILITY ANALYSIS OF HEATED FLEXIBLE PANEL IN SHOCK-DOMINATED FLOWS

Ye Liuqing²⁾^,, Ye Zhengyin

School of Aeronautics，Northwestern Polytechnical University，Xi’an 710072，China

中图分类号: O322,V215.3

文献标识码: A

收稿日期: 2017-07-4

接受日期: 2017-07-4

网络出版日期: 2018-03-20

作者简介:

作者简介：2)叶柳青，硕士研究生，主要研究方向：高超声速气动弹性. E-mail: yeliuqing0512@126.com

展开

摘要

针对激波主导流动下弹性壁板的热气动弹性稳定性分析问题,建立了基于当地活塞流理论的分析模型,并用数值仿真方法来验证其正确性. 首先基于Hamilton原理和Von-Karman大变形理论,建立壁板的热气动弹性运动方程,其中假设壁板受热后温度均匀分布,激波前后区域的气动力模型采用当地一阶活塞流理论;利用Galerkin方法将具有连续参数系统的偏微分颤振方程离散为有限个自由度的常微分方程;基于李雅普诺夫间接法将非线性颤振方程组在平衡位置处进行线化,再用Routh-Hurwits判据来判断线性系统的稳定性,从而来推论出非线性颤振系统的气动弹性稳定性. 在时域中采用龙格--库塔法对非线性颤振方程进行数值积分,得到壁板非线性颤振响应的时间历程,与理论分析结果进行对比. 研究结果表明,壁板受到斜激波冲击时,更容易发生颤振失稳,并且激波强度越大,极限环幅值和频率越大;激波主导流场中的壁板失稳边界不同于传统单纯超声速气流中壁板颤振的失稳边界;只有在斜激波前后不同的动压值都满足颤振稳定性边界的条件下,壁板才可能保持其气动弹性稳定性.

关键词： 激波 ; 热气动弹性 ; 稳定性 ; 壁板颤振 ; 当地活塞流理论

Abstract

In order to analyze the aeroelastic stability of heated flexible panel in shock-dominated flows, a systematic theoretical analysis model is established, and then test its correctness by the numerical simulation method. First of all, based on Hamilton principle and Von-Karman large deflection plate theory, the coupled partial differential governing equations are established with thermal effect based on quasi-steady thermal stress theory. Local first-order piston theory is employed in the region before and after shock waves. The Galerkin discrete method is employed to truncate the partial differential equations into a set of ordinary differential equations. The nonlinear flutter equation is linearized in the equilibrium position based on Lyapunov indirect method,and then Routh-Hurwits criterion is employed to analyze stability of the linear system. Finally, aeroelastic stability of the nonlinear flutter system is obtained. In order to verify the correctness of theoretical results, the nonlinear flutter equations are solved by the fourth-order Runge-Kutta numerical integration method to obtain time history of panel response. The results show that stability of the panel is reduced in the presence of the oblique shock. In other words, the heated panel becomes aeroelastically unstable at relatively small flight aerodynamic pressure. And the LCO amplitude and frequency are observed to increase with shock strength; the stability boundaries of heated flexible panel in shock-dominated flows are distinct from that in regular supersonic flows; only if the non-dimensional dynamic pressure upstream of the shock impingement location and the non-dimensional dynamic pressure downstream of the shock impingement location of the panel satisfy critical condition of flutter stability, will the heated panel be aeroelastically stable.

Keywords： Key words shock waves ; aerothermoelasticity ; stability ; panel flutter ; local piston theory

PDF (2526KB) 元数据多维度评价相关文章收藏文章

本文引用格式导出 EndNote Ris Bibtex

叶柳青, 叶正寅. 激波主导流动下壁板的热气动弹性稳定性理论分析[J]. 力学学报, 2018, 50(2): 221-232 https://doi.org/10.6052/0459-1879-17-242

Ye Liuqing, Ye Zhengyin. AEROELASTIC STABILITY ANALYSIS OF HEATED FLEXIBLE PANEL IN SHOCK-DOMINATED FLOWS[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(2): 221-232 https://doi.org/10.6052/0459-1879-17-242

引言

壁板颤振是飞行器表面蒙皮在气动力、惯性力和弹性力的耦合作用下而发生的一种自激振动. 这种自激振动的发生是由于气流中的能量转移到了壁板中^[1]. 如果气流仅作用在壁板的一个面上,则称之为经典壁板颤振. 壁板颤振振动的幅值一般受到结构非线性的限制不会引发迅速的破坏,而更多的是造成结构的疲劳损伤. 虽然不同于机翼颤振一定会导致严重的飞行事故,但是剧烈的壁板颤振将会对壁板结构的疲劳寿命甚至飞行器的飞行性能产生不利的影响^[2].

Jordan ^[3]最早发现壁板颤振现象,他认为大量V-2火箭在早期试验中失效,是因为火箭头部的壁板发生了颤振. 然而,对壁板颤振进行系统的研究始于20世纪50年代^[4,5]. Dowell ^[6]全面综述了前人在壁板颤振分析所做的工作,根据结构是线性还是非线性以及所使用的气动力理论进行了分类. Cheng等^[7]在Dowell的基础上,将分析模型扩展到六类,并总结了各种气动力理论适用的马赫数范围. 20世纪60年代,Dowell ^[4]采用Von-Karman 板理论和一阶活塞理论,基于伽辽金法建立了二维壁板的气动弹性模型,成为壁板颤振研究中的一个经典案例. 由于该模型具有简单的数学表达式,许多研究者基于该模型进行了壁板颤振的机理研究^[8,9],并且发展了壁板颤振模型的降阶方法^[10]和数值分析方法^[11]. Olson ^[12]发展了用有限元方法来研究壁板颤振问题,为分析任意形状、载荷条件和边界条件的壁板振动提供了可能. Gray等^[13]分析了复合材料壁板的非线性颤振,并提出了频域内求解壁板的非线性颤振方程的LUM/NTF降阶方法. Azzouz等^[14]对受气流偏角影响的壁板颤振进行了分析,并研究了有气流偏角的二维和三维柱状壁板结构的非线性颤振特性.

国内在壁板颤振方面也做了大量的工作. 夏巍等^[15]发现了二次失稳型颤振这种新的动态失稳现象,并研究了气流速压、壁板温升和初始扰动等因素对壁板的二次失稳型颤振特性的影响. 杨智春等^[16]研究了不同温度分布对复合材料壁板的颤振临界速压和非线性极限环颤振幅值的影响. 叶献辉等^[17]基于活塞流理论,研究了热环境下壁板大气紊流的动力响应特性,并分析了来流平均动压、温度、紊流强度及紊流尺度等参数对壁板结构均方根响应值的影响. 杨超等^[2]建立了气动热、气动弹性双向耦合高超声速二维曲面壁板颤振分析方法,发现基于这种双向耦合的壁板分析结果更加危险. 赵海等^[18]利用3阶非线性活塞理论进行气动力建模,研究了动态吸振器对高超声速流中复合材料壁板颤振的抑制作用. 上述研究都是针对壁板只一个表面受气流作用影响. 周建等^[19]通过解析分析和数值计算的手段研究了两面受气动载荷的壁板的热气动弹性稳定性,结果表明壁板两面同时作用气动载荷时更容易发生颤振失稳.

对于超声速和高超声速飞行器而言^[20,21],不同部件之间存在着多体干扰问题,一个部件的激波会作用在其他部件的壁面上^[22];在发动机的流道内部,流场中也存在复杂的波系;这些现象的共同之处就是激波主导下的壁面颤振问题,因此研究激波作用的流场中薄壁板的热气动弹性问题很有必要^[23]. 目前国内外已有学者对此问题展开研究,Visbal ^[24]通过完全可压缩的N-S方程来求解变形壁板上的无黏流场,从数值的角度研究了二维弹性壁板在激波作用下的动力学特性,结果表明当激波强度较大时,临界颤振动压远小于没有激波作用时壁板的临界颤振动压,稳定性明显降低. Visbal ^[25]在2014年进一步通过求解Euler和N-S方程研究了无黏和黏性流场中受激波作用的二维壁板的气动弹性,并分析激波位置对稳定性的影响. Brouwer等^[23]提出了用当地活塞流理论来预测有激波作用的流场中气动力的可行性. Yao等^[26]通过完全流固耦合(FSI)方法研究了壁面振动对跨音速扩散段中的气动力的影响. 然而,上述的研究也都是从数值角度进行分析,不能够得到系统参数间的定性规律,并且也只针对壁板只一面受气动荷载的情况. 目前从公开发表的文献看,还没有学者从解析理论的角度,研究斜激波作用下壁板的热气动弹性稳定性.

本文针对激波主导流动下壁板的热气动弹性稳定性分析问题,建立了基于当地活塞流理论的分析模型,并用数值仿真方法来验证其正确性. 基于此理论模型分别研究了只一面作用气动载荷及两面同时存在不同动压流场的薄壁板受斜激波冲击时的热气动弹性稳定性,并给出使壁板发生气动弹性失稳的边界条件. 研究工作不仅从理论上加深了对受热壁板在斜激波作用下的非线性动力学行为的理解,研究结论对高超声速飞行器壁板设计也有一定的参考价值.

1 壁板在激波主导流动下的运动方程

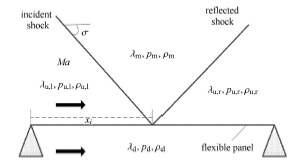
考虑一个二维各向同性材料的壁板,边界条件为两端简支,如图1所示. 壁板的上表面流场中有入射斜激波和反射激波作用,下表面有超音速气流流过. 壁板上表面入射斜激波前的气流密度、速度和马赫数分别为 $ρ_{u, l}, U_{u, l}, M a_{u, l}$ ,反射斜激波后的气流密度、速度和马赫数分别为 $ρ_{u, r}, U_{u, r}, M a_{u, r}$ ,壁板下表面的气流密度、速度和马赫数分别为 $ρ_{d}, U_{d}, M a_{d}$ . 基于Hamilton原理和 Von Karman大变形板弯理论,壁板在激波主导流动下的气动弹性运动方程为

$D \partial^{4} w \partial x^{4} - (N_{x} - N_{x}^{(T)}) \partial^{2} w \partial x^{2} + ρ h \partial^{2} w \partial t^{2} + p (x, t) = 0$ (1)

其中, $w$ 为壁板振动位移; $D = E h^{3} / [12 (1 - υ^{2})]$ 为壁板的抗弯刚度; $E$ 为材料的弹性模量; $υ$ 为泊松比; $ρ, l, h$ 分别代表壁板的密度、长度和厚度, 几何非线性效应引起的壁板附加面内力为

$N_{x} = Eh 2 l (1 - υ^{2}) \int_{0}^{l} ‍ {(\partial w \partial x)}^{2} dx$

假设壁板受热并达到稳态后温度均匀分布,由温升 $Δ T = T - T_{0}$ 引起的面内力为

$N_{x}^{(T)} = \int_{-}^{h} ‍ E α Δ Tdz = Eh α Δ T$ (2)

在这里只考虑壁板温升导致的附加面内力的变化,其中 $T_{0}$ 为初始温度, $α$ 为材料的热膨胀系数.

显示原图| 下载原图ZIP| 生成PPT

图1 受斜激波冲击的二维壁板

Fig. 1 Schematic of flow configuration for oblique shock impinging on a flexible panel

在减缩频率 $w^{*} = wl / U ≪ 1$ 的条件下,基于一阶活塞理论的超音速气动公式为

$p - p_{\infty} = 2 q β (\partial w \partial x + M_{\infty}^{2} - 2 M_{\infty}^{2} - 11 U_{\infty} \partial w \partial t)$ (3)

为了有效预测激波主导流场中的气动力,采用当地一阶活塞流理论,文献[23]已经证实当地活塞流理论预测激波主导流场下气动力的可行性. 在当地活塞流理论中,相应的自由来流流动参数用当地参数来代替, 得到壁板上、下表面的气动力分别如下.

上表面入射斜激波前

$p_{u, l} = p_{u, l}^{*} + 2 q_{u, l} β_{u, l} (\partial w \partial x + M a_{u, l}^{2} - 2 M a_{u, l}^{2} - 11 U_{u, l} \partial w \partial t)$ (4)

上表面反射斜激波后

$p_{u, r} = p_{u, r}^{*} + 2 q_{u, r} β_{u, r} (\partial w \partial x + M a_{u, r}^{2} - 2 M a_{u, r}^{2} - 11 U_{u, r} \partial w \partial t)$ (5)

下表面

$p_{d} = p_{d}^{*} - 2 q_{d} β_{d} (\partial w \partial x + M a_{d}^{2} - 2 M a_{d}^{2} - 11 U_{d} \partial w \partial t)$ (6)

其中, $p_{u, l}^{*}$ , $p_{u, r}^{*}$ 分别为作用于壁板上表面入射斜激波前、后的静压; $p_{d}^{*}$ 为作用于壁板下表面的静压. 下标u, d 分别代表上、下表面,l, r 分别代表左、右端. $β_{u, l (r)} = \sqrt{M a_{u, l (r)}^{2} - 1}$ , $β_{d} = \sqrt{M a_{d}^{2} - 1}$ 为Prandtl-Glauert因子. $q_{u, l (r)} = ρ_{u, l (r)} U_{u, l (r)}^{2} / 2$ , $q_{d} = ρ_{d} U_{d}^{2} / 2$ 为动压.

为了从解析的角度分析此问题,并且使复杂问题简单化,这里假设 $p_{u, l}^{*} = p_{d}^{*}$ , $p_{u, r}^{*} = p_{d}^{*}$ ,即壁板初始时刻处上下静压平衡. 这种假设具有一定的工程背景,对于热防护系统中的隔热层来说,它具有只隔热不传力的特点. 因此本文不考虑激波引起的静压差(也就是静变形)对壁板稳定性的影响,而是从理论上重点讨论激波引起的非定常动压差对壁板颤振边界的影响.

进一步得到入射斜激波前上下压差

$\begin{array}{l} p_{u, l} - p_{d} = 2 q_{u, l} β_{u, l} (\partial w \partial x + M a_{u, l}^{2} - 2 M a_{u, l}^{2} - 11 U_{u, l} \partial w \partial t) + 2 mm] 2 q_{d} β_{d} (\partial w \partial x + M a_{d}^{2} - 2 M a_{d}^{2} - 11 U_{d} \partial w \partial t) \end{array}$ (7)

反射斜激波后上下压差

$\begin{array}{l} p_{u, r} - p_{d} = 2 q_{u, r} β_{u, r} (\partial w \partial x + M a_{u, r}^{2} - 2 M a_{u, r}^{2} - 11 U_{u, r} \partial w \partial t) + 2 mm] 2 q_{d} β_{d} (\partial w \partial x + M a_{d}^{2} - 2 M a_{d}^{2} - 11 U_{d} \partial w \partial t) \end{array}$ (8)

引入无量纲参数

$\begin{array}{l} ξ = x / l, τ = t \sqrt{D / ρ h l^{4}}, \bar{p} = (l^{4} / Dh) p 2 mm] λ_{u, l (r)} = 2 q_{u, l (r)} l^{3} / β_{u, l (r)} D \\ lambd a_{d} = 2 q_{d} l^{3} / β_{d} D, W = w / h \\ m u_{u, l (r)} = ρ_{u, l (r)} / ρ h, μ_{d} = ρ_{d} l / ρ h 1.5 mm 2.8 m m_{x}^{(T)} = N_{x}^{(T)} l^{2} / D 1.5 mm 2.8 m m_{x} = N_{x} l^{2} / D = 6 \int_{0}^{1} ‍ {(\partial W / \partial ξ)}^{2} d ξ 1.5 mm 2.8 m m_{Mu, l (r)} = (M a_{u, l (r)}^{2} - 2 M a_{u, l (r)}^{2} - 1) μ_{u, l (r)} β_{u, l (r)}, R_{Md} = {(M a_{d}^{2} - 2 M a_{d}^{2} - 1)}^{2} μ_{d} β_{d} \end{array}$ 代入式(1)得到壁板的无量纲运动方程

$\partial^{2} W \partial τ^{2} - (R_{x} - R_{x}^{(T)}) \partial^{2} W \partial ξ^{2} + \partial^{4} W \partial ξ^{4} + \bar{p} = 0$ (9)

采用Galerkin方法将方程离散,将位移函数展开成各阶谐波模态的叠加. 对于简支边界条件,位移函数为

$W (ξ, τ) = \sum_{i}^{=} ‍ q_{i} (τ) \sin (i πξ)$ (10)

将式(10)代入方程(9)中,对方程的各项同时乘以 $\sin j π x (j = 1,2, \dots, \infty)$ ,并沿着板长积分.

由于激波的存在,壁板左右两端压差不同,采用 Galerkin方法对气动力项处理如下,从而将激波影响引入气动弹性方程中

$\int_{0}^{1} ‍ \bar{p} \sin (j π x) d ξ = \int_{0}^{0.5} ‍ (\bar{p_{u, l}} - \bar{p_{d}}) \sin (j π x) d ξ + \int_{0.5}^{1} ‍ (\bar{p_{u, r}} - \bar{p_{d}}) \sin (j π x) d ξ (11)$

以上可得到离散后的壁板运动方程,为减缩分析的规模,假设壁板变形以前 $N$ 阶谐波模态为主,即只用前 $N$ 阶谐波的叠加来构成壁板的位移函数,并记 $\dot{q} = \partial q / \partial τ$ , $\ddot{q} = (\partial q / \partial τ) / \partial τ$ ,得到降阶后的壁板运动的状态空间方程

$\begin{array}{l} {\ddot{q}}_{j} (τ) + [{(j π)}^{4} - R_{x}^{(T)} {(j π)}^{2}] q_{j} (τ) + 2 mm] 3 {(j π)}^{2} q_{j} (τ) \sum_{i}^{=} ‍ {(i π)}^{2} q_{i}^{2} (τ) + q^{*} = 0 \end{array}$ (12)

式中

$q^{*} = q_{1} + q_{2} + q_{3} + q_{4} + q_{5} + q_{6}$

$q_{1} = 12 (λ_{u, l} + λ_{d}) q_{j} (τ) [1 - \cos (j π)] + (\sqrt{λ_{u, l} R_{Mu, l}} + \sqrt{λ_{d} R_{Md}}) \sqrt{λ_{u, l} R_{Mu, l}} {\dot{q}}_{j} (τ) [12 - 12 j π \sin (j π)] q_{2} = 2 \sum_{i}^{\neq} ‍ (λ_{u, l} + λ_{d}) q_{i} (τ) (i π) \{(- 121 j π + i π) [\cos (12 j π + 12 i π) - 1] + (- 121 j π - i π) [\cos (12 j π - 12 i π) - 1]\} q_{3} = 2 \sum_{i}^{\neq} ‍ (\sqrt{λ_{u, l} R_{Mu, l}} + \sqrt{λ_{d} R_{Md}}) {\dot{q}}_{i} (τ) [12 (j π - i π) \sin (12 j π - 12 i π) - 12 (j π + i π) \sin (12 j π + 12 i π)] q_{4} = (λ_{u, r} + λ_{d}) q_{j} (τ) (j π) [- 12 j π \cos (2 j π) + 12 j π \cos (j π)] + (\sqrt{λ_{u, r} R_{Mu, r}} + \sqrt{λ_{d} R_{Md}}) {\dot{q}}_{j} (τ) [12 - 12 j π \sin (2 j π) + 12 j π \sin (j π)] q_{5} = 2 \sum_{i}^{\neq} ‍ (λ_{u, r} + λ_{d}) q_{i} (τ) (i π) [- 121 j π + i π \cos (j π + i π) + 121 j π + i π \cos (12 j π + 12 i π)] + 2 \sum_{i}^{\neq} ‍ (λ_{u, r} + λ_{d}) q_{i} (τ) (i π) [- 121 j π - i π \cos (j π - i π) + 121 j π - i π \cos (12 j π - 12 i π)] q_{6} = 2 \sum_{i}^{\neq} ‍ (\sqrt{λ_{u, r} R_{Mu, r}} + \sqrt{λ_{d} R_{Md}}) {\dot{q}}_{i} (τ) [121 j π - i π \sin (j π - i π) - 121 j π - i π \sin (12 j π - 12 i π)] + 2 \sum_{i}^{\neq} ‍ (\sqrt{λ_{u, r} R_{Mu, r}} + \sqrt{λ_{d} R_{Md}}) {\dot{q}}_{i} (τ) [- 121 j π + i π \sin (j π + i π) + 121 j π + i π \sin (12 j π + 12 i π)]$

式(12)为推导出的壁板在激波主导流动下的状态空间方程,将其与其他文献结果对比以验证其结果正确性. 将 $λ_{u, l} = λ_{u, r}$ 代入上式中,即为无激波但壁板两面存在不同动压流场的情况,得到结果与文献[19]推导结果一致. 将 $λ_{u, l} = λ_{u, r}$ , $λ_{d} = 0$ 代入上式,即为经典壁板颤振情况,得到结果与文献[9]结果一致.

2 壁板热颤振稳定性的解析分析

式(12)是一个高维的非线性自治系统,为了从解析的角度对系统的动力学特性进行分析. 这里以二阶受热壁板气动弹性系统( $N = 2$ )为例,并令 ${\dot{q}}_{i} = q_{N + i}$ ,得到受热壁板气动弹性状态方程为

$\begin{array}{l} {\dot{q}}_{1} = q_{3}, {\dot{q}}_{2} = q_{4} 2 mm] {\dot{q}}_{3} = - π^{2} (π^{2} - R_{x}^{(T)}) q_{1} - 3 π^{4} q_{1} (q_{1}^{2} + 4 q_{2}^{2}) - (λ_{u, l} - λ_{u, r}) q_{1} + [43 (λ_{u, l} + λ_{u, r}) + 83 λ_{d}] q_{2} - \\ qquad [12 (\sqrt{λ_{u, l} R_{Mu, l}} + \sqrt{λ_{u, r} R_{Mu, r}}) + \sqrt{λ_{d} R_{Md}}] {\dot{q}}_{1} - 43 π (\sqrt{λ_{u, l} R_{Mu, l}} - \sqrt{λ_{u, r} R_{Mu, r}}) {\dot{q}}_{2} 2 mm] {\dot{q}}_{4} = - 4 π^{2} (4 π^{2} - R_{x}^{(T)}) q_{2} - 12 π^{4} q_{2} (q_{1}^{2} + 4 q_{2}^{2}) - [43 (λ_{u, l} + λ_{u, r}) + 83 λ_{d}] q_{1} - \\ qquad [12 (\sqrt{λ_{u, l} R_{Mu, l}} + \sqrt{λ_{u, r} R_{Mu, r}}) + \sqrt{λ_{d} R_{Md}}] {\dot{q}}_{2} - 43 π (\sqrt{λ_{u, l} R_{Mu, l}} - \sqrt{λ_{u, r} R_{Mu, r}}) {\dot{q}}_{1} \end{array}\} (13)$

当式(13)中的所有状态变量对时间的导数项都等于零时对应的方程为壁板的静气动弹性方程. 可以看出 $q_{1} = q_{2} = 0$ 是系统的一个静平衡解,该解对应着无变形的壁板平衡状态. 采用李雅普诺夫间接法来判断该不动点的稳定性,分析激波作用下受热壁板的热颤振稳定性.

设系统的变形 $\bar{q_{i}}$ 由静变形 $q_{i}$ 和小扰动量 $ε_{i}$ 组成,即 $\bar{q_{i}} = q_{i} + ε_{i}$ , $\bar{q_{N + i}} = ε_{N + i} (i = 1,2, \dots, N)$ . 则在壁板平衡状态下,系统的状态方程(13)可以线化为 $\dot{ε} = A ε$ ,其中 $A$ 为式(13)在壁板平衡状态处的Jacobian矩阵. 设 $ε_{i} = ε_{i 0} e^{Ω τ}$ ,可以得到伴随线性系统的特征方程为

$|A - Ω I| = 0$ (14)

其中复特征值 $Ω = Ω_{R} \pm i Ω_{I}$ ,当 $Ω_{R} < 0$ 时,伴随系统渐进稳定; $Ω_{R} > 0$ ,伴随系统不稳定.

因此,结合线性稳定性定理可进一步推论出对应的非线性系统的性质. 以二阶系统( $N = 2$ )为例,说明李雅普诺夫间接法分析激波作用下壁板的稳定性过程. 显然,对于二阶受热壁板气动弹性系统, $q_{1} = q_{2} = 0$ 是系统的一个静平衡解,在该平衡点处,其Jacobian矩阵为如下

$A = [\begin{array}{l} 0 & 0 & 12 mm] 0 \\ 0 & 02 mm] π^{2} (R_{x}^{(T)} - π^{2} + λ_{u, r} - λ_{u, l} π^{2}) & 83 [12 (λ_{u, l} + λ_{u, r}) + λ_{d}] \\ - 12 (\sqrt{λ_{u, l} R_{Mu, l}} + \sqrt{λ_{u, r} R_{Mu, r}}) - \sqrt{λ_{d} R_{Md}} 2 mm] - 83 [12 (λ_{u, l} + λ_{u, r}) + λ_{d}] & 4 π^{2} (R_{x}^{(T)} - 4 π^{2}) & 43 π \sqrt{λ_{u, r} R_{Mu, r}} - 43 π \sqrt{λ_{u, l} R_{Mu, l}} \end{array} \begin{array}{l} 0 {43 π \sqrt{λ_{u, r} R_{Mu, r}} - 43 π \sqrt{λ_{u, l} R_{Mu, l}} {- 12 (\sqrt{λ_{u, l} R_{Mu, l}} + \sqrt{λ_{u, r} R_{Mu, r}}) - \sqrt{λ_{d} R_{Md}} \end{array}]$ (15)

线性系统的特征方程为

$|A - Ω I| = Ω^{4} + A_{3} Ω^{3} + A_{2} Ω^{2} + A_{1} Ω + A_{0} = 0$ (16)

根据Routh-Hurwits判据. 系统所有特征值 $Ω$ 实部为负的充要条件为

$A_{3}, A_{2}, A_{1}, A_{0} > 0$ (17a)

$A_{3} A_{2} - A_{1} > 0$ (17b)

$A_{3} A_{2} A_{1} - A_{1}^{2} - A_{3}^{2} A_{0} > 0$ (17c)

令激波前后无量纲动压比为 $n = λ_{u, r} λ_{u, l}$ ,壁板上表面激波前、下表面的无量纲动压比为 $m = λ_{d} λ_{u, l}$ .

设无气流作用时壁板的临界屈曲温升为 $Δ T_{cr}$ ,引入无量纲温升比

$Δ T / Δ T_{cr} = R_{x}^{(T)} / π^{2}$ (18)

由判别式(17a)和式(17b)得到

$(n - 1) λ_{u, l} < π^{4} (17 - 5 Δ T Δ T_{cr}) (19) λ_{u, l} > 34 π^{4} \sqrt{- [Δ T Δ T_{cr} - 1 + (n - 1) λ_{u, l} π^{4}] (Δ T Δ T_{cr} - 4)} 12 (n + 1) + m (20)$

由于壁板的材料密度比相对空气密度要大得多,因此质量参数 $R_{Mu, l}, R_{Mu, r}, R_{Md}$ 都是很小的值,并且从文献[9]的研究结论可知,质量参数对壁板稳定边界影响很小,在壁板颤振稳定性边界特性分析中可以忽略,因此可以由判别式(17c)得到保守解

$λ_{u, l} < 9 π^{4} (5 - Δ T Δ T_{cr}) (5 n + 11) + 16 m$ (21)

基于二阶谐波模型来分析壁板的后屈曲稳定性,受热壁板的静气动弹性方程如下

$\begin{array}{l} π^{2} [π^{2} - R_{x}^{(T)} + π^{2} H + (1 - n) λ_{u, l} π^{2}] q_{1} - 2 mm] 83 [12 (1 + n) λ_{u, l} + λ_{d}] q_{2} = 02 mm] 83 [12 (1 + n) λ_{u, l} + λ_{d}] q_{1} + \\ qquad 4 π^{2} (4 π^{2} - R_{x}^{(T)} + π^{2} H) q_{2} = 0 \end{array}\}$ (22)

其中 $H = 3 (q_{1}^{2} + 4 q_{2}^{2})$ .

$q_{1}, q_{2}$ 有非零解的充要条件是

$\begin{array}{l} H = - 52 + Δ T Δ T_{cr} - (1 - n) λ_{u, l} 2 π^{4} \pm \\ quad 16 π^{4} \sqrt{9 {[(1 - n) λ_{u, l} - 3 π^{4}]}^{2} - 64 {[12 (1 + n) λ_{u, l} + λ_{d}]}^{2}} \end{array}$ (23)

要 $H$ 为实数,则壁板的无量纲动压必须满足

$λ_{u, l} # x 2264; 9 π^{4} n + 7 + 8 m$ (24)

式(19) $~$ 式(21)和式(24)共同确定了上侧有激波主导的流场,下侧有超音速气流流过的受热壁板颤振稳定性边界. $n = 1$ 表示不考虑激波的影响, $m = 0$ 表示不考虑壁板下表面的超音速气流作用. 文献[19]中推导出了没有激波存在但双面受超音速气流作用的受热壁板的稳定性边界,将 $n = 1$ , $m λ_{u, l} = λ_{d}$ 代入上式中得到稳定性边界并与其比较,可见结果与文献[19]的结果完全一致. 文献[9]中推导出了单面受气动载荷的壁板颤振稳定性,将 $n = 1$ , $m = 0$ 代入上式中得到的结果与文献[9]的结果比较,结果完全一致.

由式(19) $~$ 式(21)和式(24)可以看出,对于单面受气动载荷并且有激波作用的壁板,只有在激波前后的动压都满足稳定性边界条件下,壁板才可能保持气动弹性稳定性;对于双面受气动载荷并且一侧有激波作用的壁板,只有在激波前后的动压以及另一侧的动压都满足稳定性边界的条件下,壁板才可能保持气动弹性稳定性.

3 激波强度对壁板稳定性的影响

关于弹性壁板在激波主导流动中的热气动弹性稳定性问题,在上节中已建立了相应的理论分析模型. 基于此理论模型,首先从解析角度系统分析激波强度对受热壁板气动稳定性的影响,然后进一步从数值仿真角度对解析结果进行验证. 马赫数和激波角是影响激波强度的关键因素,并且马赫数和激波角越大,激波强度越大. 这里通过改变激波角来改变激波强度. 取定波前马赫数为 $Ma = 3.5$ ,改变激波角,通过斜激波关系式计算入射激波前与反射激波后的无量纲动压比 $n$ ,如表1所示.

表1 不同激波角下的动压比

Table 1 Dynamic pressure ratios $n$ with different shock angle $σ$

Shock angle	Pressure ratio	Dynamic pressure ratio
$σ$ /(#x00B0;)	$p_{u, r} / p_{u, l}$	$n$
	1.486 2	1.380 2
	3.295 5	2.596 9
	6.362 2	4.256 0
	8.278 8	5.149 2
	10.422 7	6.074 8
	13.440 2	7.390 8

新窗口打开

3.1 解析分析

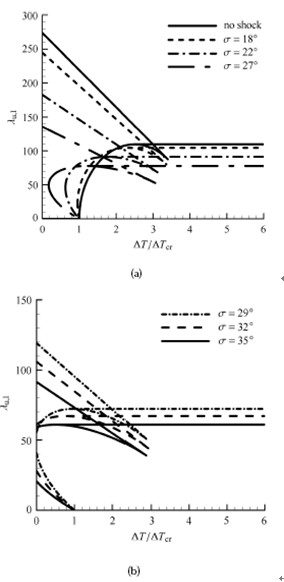
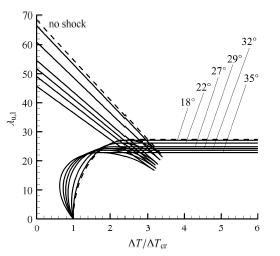
首先分析激波作用下单面受超音速气动载荷的壁板的稳定性,即 $m = 0$ . 将表1中不同的激波强度对应的无量纲动压比 $n$ 代入式(19) $~$ 式(21)和式(24)中,可绘制出受热壁板的气动弹性稳定性边界见图2和图3. 由图2(a)和图2(b)可以看出,激波的存在使发生颤振的临界动压变小,受热壁板的稳定性降低. 并且随着激波角的增大,动态失稳边界在下降,稳定区域面积在逐渐减小. 随着激波强度的增大,在温升不变的情况下,气动弹性临界稳定动压会明显减小;并且在温升较小时,气动弹性临界稳定动压的增量随着温升的增大而减小,而当温升较大时,气动弹性临界稳定动压的增量保持不变.

显示原图| 下载原图ZIP| 生成PPT

图2 激波强度对气动弹性稳定性边界的影响(单面)

Fig. 2 Stability boundaries with different incident shock strength (one surface)

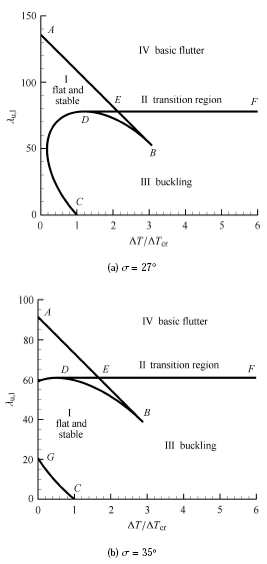
从图3(a)和图3(b)可见,激波主导流场中的壁板失稳边界不同于传统单纯超声速气流中壁板颤振的失稳边界而呈现新的特征,并且随着激波强度不同,稳定性边界呈现不同的特征. 图2(a)中的几种激波强度情况呈现的特征对应图3(a),图3(a)示出了 $σ = 2 7^{\circ}$ 时受热壁板的气动弹性稳定性边界. 当激波强度不大时,气动弹性稳定性边界线仍将平面分成4个区域：壁板的渐近稳定区、屈曲区(静态失稳)、基本型颤振区(动态失稳)和过渡稳定区(DBE区). 在壁板的渐近稳定区,壁板最终稳定在平壁板状态;在屈曲区,壁板最终将稳定在屈曲变形状态;在基本型颤振区,壁板将发生极限环运动,甚至混沌运动等复杂非线性动力学行为;而在过渡稳定区,壁板可能稳定在平壁板状态,也可能稳定在屈曲变形状态. 由图2(a)可见,随着激波强度的增大,渐近稳定区的面积和屈曲区的面积都在减小,基本型颤振区的面积在增大. 除此之外,可见静态屈曲失稳边界CDB在向 $λ_{u, l}$ 轴扩展. 当没有激波作用时,壁板在温升 $Δ T > Δ T_{cr}$ 时才发生屈曲,而当有一定强度的激波作用时,温升小于 $Δ T_{cr}$ 壁板就会发生屈曲. 可见,在激波作用下,受热壁板更容易发生屈曲,并且随着激波强度的增大,壁板的临界屈曲温升也随之减小.

显示原图| 下载原图ZIP| 生成PPT

图3 壁板的稳定性区域图(单面)

Fig. 3 Stability boundary(one surface)

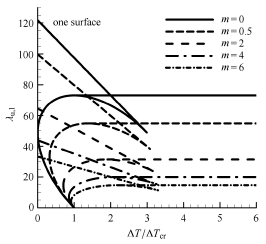
当激波强度较大时,受热壁板的气动弹性稳定性边界如图2(b)和图3(b)所示. 图2(b)中的几种激波强度情况呈现的特征对应图3(b),图3(b)示出了 $σ = 3 5^{\circ}$ 时受热壁板的气动弹性稳定性边界. 由图可见,当激波强度较大时,气动弹性稳定性边界线将平面分成5个部分,但仍然是上述4种不同性质的区域,之前连续的渐进稳定区被屈曲区隔开成为两部分;还可以看出当激波强度较大时,即使温升为零时受热壁板也会发生屈曲,即受热壁板只在激波作用下也会发生屈曲. 并且随着激波强度的增大,在温升为零的情况下,能使壁板发生屈曲的范围也越大.

图4示出了激波作用下双面受气动载荷的受热壁板的气动弹性稳定性边界,取 $m = 3$ . 由图可见,双面受气动载荷的受热壁板在激波作用下,稳定性也是降低的,随着强度的增大,稳定性在不断降低,其他特征也大致相同. 不过与单面情况相比,在两面受气动载荷的情况中,气动弹性稳定性边界对于激波强度的变化敏感度降低. 改变激波强度,双面受气动载荷的受热壁板的气动弹性稳定性边界的改变较小,发生颤振的临界动压的改变量较小. 即使在较大强度的激波作用下,气动弹性稳定性边界线仍将平面分成4个区域.

显示原图| 下载原图ZIP| 生成PPT

图4 激波强度对气动弹性稳定性边界的影响(双面)

Fig. 4 Stability boundaries with different incident shock strength (both surfaces)

3.2 数值仿真

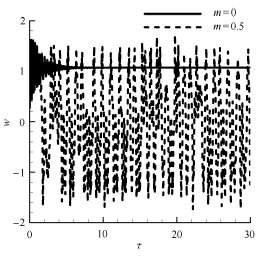
本节从数值仿真角度来验证解析分析的正确性,主要以单面为例( $m = 0$ ). 采用固定时间步长的四阶Runge-Kutta法对非线性颤振方程(即式(13))进行数值积分. 取无量纲时间步长 $Δ τ = 0.001$ ,初值为 $(q_{1}, q_{2}, q_{3}, q_{4}) = (0.5,0.5,0, 0)$ ,观察点为 $ξ = 0.75$ .

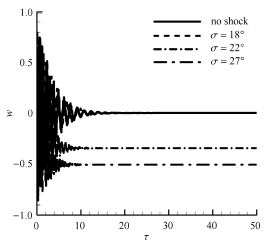
验证点取 $(Δ T = Δ T_{cr}, λ_{u, l} = 200)$ ,数值仿真结果如图5. 从图2(a)解析结果可得,对于此验证点,无激波时,壁板渐进稳定, $σ = 1 8^{\circ}$ , $2 2^{\circ}$ , $2 7^{\circ}$ 时,壁板失稳表现为颤振. 由图5可见,没有激波作用时,位移值收敛到零,即在初始扰动下,受热壁板将恢复到初始平衡位置;当有激波作用时 $(σ = 1 8^{\circ}$ , $2 2^{\circ})$ ,壁板的稳态响应表现为等幅的间谐振荡,位移--速度相图曲线均为一个封闭的椭圆, 这里限于篇幅没有展示,即为一种单谐波极限环振荡. 当激波强度增大到 $σ = 2 7^{\circ}$ ,颤振响应是多谐波的极限环振荡. 进行更多的仿真发现激波强度较大时较多出现多谐波极限环振荡甚至混沌. 由此可见,数值仿真结果与解析分析结果完全一致,得到激波的作用使受热壁板的稳定性降低. 从数值仿真结果可进一步看出,随着激波强度增大,极限环幅值与频率增大.

显示原图| 下载原图ZIP| 生成PPT

图5 时间历程( $Δ T = Δ T cr, λ u, l = 200)$

Fig. 5 Time history for $Δ T = Δ T cr, λ u, l = 200$

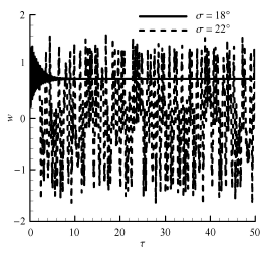
验证点取 $(Δ T / Δ T_{cr}, λ_{u, l}) = (1,50)$ ,数值仿真结果如图6. 图2(a)解析结果显示,无激波和 $σ = 1 8^{\circ}$ 时,壁板渐进稳定, $σ = 2 2^{\circ}, 2 7^{\circ}$ 时,壁板进入屈曲区. 由图6可见,对于无激波和 $= a_{i} + ε_{i}$ ,响应随时间衰减收敛到零.

显示原图| 下载原图ZIP| 生成PPT

图6 时间历程( $Δ T = Δ T cr, λ u, l = 50$ )

Fig. 6 Time history for $Δ T = Δ T cr, λ u, l = 50$

对于 $σ = 2 2^{\circ}, 2 7^{\circ}$ ,响应随时间衰减并收敛到一个常数值(不为零). 数值仿真结果与解析分析结果一致. 进一步验证在激波作用下,受热壁板更容易发生屈曲,并且随着激波强度的增大,壁板的临界屈曲温升也随之减小.

验证点取 $(Δ T / Δ T_{cr}, λ_{u, l}) = (4,100)$ ,数值仿真结果如图7. 解析结果表示在此点,当无激波和 $σ = 1 8^{\circ}$ 时,壁板进入屈曲区, $σ = 2 2^{\circ}, 2 7^{\circ}$ 时,壁板进入基本型颤振区. 而由图7可见,对于 $σ = 1 8^{\circ}$ ,响应随时间衰减并收敛到一个常数值(不为零). 对于 $σ = 2 2^{\circ}$ ,稳态响应表现为混沌振荡. 数值仿真结果与解析分析结果一致.

显示原图| 下载原图ZIP| 生成PPT

图7 时间历程 ( $Δ T = 4 Δ T cr, λ u, l = 100)$

Fig. 7 Time history for $Δ T = 4 Δ T cr, λ u, l = 100$

图8示出了 $Δ T = 0$ , $λ_{u, l} = 35$ 时,受热壁板的无量纲位移的时间历程曲线. 它验证了当激波强度较大时,即使温升为零,只在激波作用下受热壁板也会发生屈曲. 由图可见,对于 $σ = 2 9^{\circ}$ ,响应随时间衰减并收敛到零,表明一段时间后壁板不再振动而稳定在初始的平衡状态. 对于 $σ = 3 2^{\circ}, 3 5^{\circ}$ ,响应随时间衰减并收敛到一个常数值(非零),表明一段时间后壁板不再振动而发生屈曲,图2(b)中解析分析得到对于 $(Δ T / Δ T_{cr}$ , $λ_{u, l}) = (0,35)$ ,对于 $σ = 2 9^{\circ}$ ,壁板渐进稳定, $σ = 3 2^{\circ}$ , $3 5^{\circ}$ 时,壁板进入屈曲区. 数值仿真结果与解析分析结果一致.

显示原图| 下载原图ZIP| 生成PPT

图8 时间历程( $Δ T = 0, λ u, l = 35)$

Fig. 8 Time history for $Δ T = 0, λ u, l = 35$

4 壁板下壁面超音速气流对稳定性的影响

基于理论模型,进一步分析壁板上壁面的激波强度确定时,下壁面不同的超音速气流对气动弹性稳定性边界的影响. 固定壁板上表面的激波强度,取 $n = 5$ , 并将不同 $m$ 值代入式(20) $~$ 式(22)和式(25)式中,得到相应的稳定性边界线如图9所示. 从图中可以看出,下壁面的超音速气流会降低受热壁板的稳定性,并且随着下壁面超音速气流的无量纲动压越大,受激波作用的受热壁板稳定性也越来越差. 基本型颤振区域的面积在增大表示此受热壁板越来越容易失稳. 然而,与激波强度的影响不同,随着下壁面超音速气流的无量纲动压增大,虽然屈曲区的面积在减小,但是临界屈曲温升却在增加. 这意味着壁板发生热屈曲需要的温升越来越大(即随着下壁面超音速气流的无量纲动压增大,受热壁板越难发生屈曲). 这是因为下壁面的超音速气流平衡了一部分上壁面的激波造成的压差.

下面从数值仿真角度来验证解析分析的正确性. 取无量纲时间步长 $Δ τ = 0.001$ ,初值取定为 $(q_{1}, q_{2}, q_{3}, q_{4}) = (0.5,0.5,0, 0)$ ,观察点为 $ξ = 0.75$ .

显示原图| 下载原图ZIP| 生成PPT

图9 壁板的稳定性边界图

Fig.9 Stability boundary

验证点取 $(Δ T / Δ T_{cr} = 0.5, λ_{u, l} = 100)$ ,数值仿真结果如图10. 从图9解析结果可知,对于此验证点,壁板下壁面无超音速气流时(即 $m = 0$ ),壁板渐进稳定, $m = 0.5$ , 2, 4, 6时,壁板失稳表现为颤振. 由图10可见,壁板下壁面无超音速气流时,位移值收敛到零,即在初始扰动下,受热壁板将恢复到平衡位置;当壁板下壁面有超音速气流作用时( $m = 0.5$ , 2, 4, 6),壁板的稳态响应表现为等幅的简谐振荡,位移--速度相图曲线均为一个封闭的椭圆这里限于篇幅没有展示,即为一种单谐波极限环振荡. 由此可见,数值仿真结果与解析分析结果完全一致. 从数值仿真结果可进一步看出,随着壁板下壁面超音速气流动压的增大,极限环振荡幅值也在增大.

显示原图| 下载原图ZIP| 生成PPT

图10 时间历程( $Δ T = 0.5 Δ T cr, λ u, l = 100)$

Fig. 10 Time history for $Δ T = 0.5 Δ T cr, λ u, l = 100$

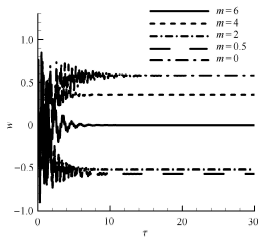
验证点取 $(Δ T / Δ T_{cr}, λ_{u, l}) = (1.5,1.5)$ ,数值仿真结果如图11. 图9解析结果显示, $m = 6$ 时,壁板渐进稳定, $m = 0$ , 0.5, 2, 4时,壁板进入屈曲区. 由图11可见,对于 $m = 6$ ,响应随时间衰减并收敛到零,表明一段时间后壁板不再振动而稳定在初始的平衡位置上. 对于 $m = 0$ , 0.5, 2, 4, 响应随时间衰减并收敛到一个常数值(非零),表明一段时间后壁板不再振动而发生屈曲. 数值仿真结果与解析分析结果一致.

显示原图| 下载原图ZIP| 生成PPT

图11 时间历程( $Δ T = 1.5 Δ T cr$ , $λ u, l = 15)$

Fig. 11 Time history for $Δ T = 1.5 Δ T cr$ , $λ u, l = 15$

图12示出了 $Δ T / Δ T_{cr} = 4, λ_{u, l} = 60$ 时,受热壁板的无量纲位移的时间历程曲线. 由图可见对于壁板下壁面无超音速气流时(即 $m = 0$ ),响应随时间衰减并收敛到一个常数值(非零). 对于 $m = 0.5$ ,稳态响应表现为混沌振荡. 图9中解析分析得到对于 $(Δ T / Δ T_{cr}, λ_{u, l}) = (4,60)$ ,当 $m = 0$ 时,壁板进入屈曲区, $m = 0.5$ 时,壁板进入基本型颤振区. 数值仿真结果与解析分析结果一致.

12 时间历程( $Δ T = 4 Δ T_{cr}$ , $λ_{u, l} = 60)$

显示原图| 下载原图ZIP| 生成PPT

Fig. 12 Time history for $Δ T = 4 Δ T cr$ , $λ u, l = 60$

5 结论

本文针对激波主导流动下壁板的热气动弹性稳定性问题,建立了基于当地活塞流理论的分析模型,并用数值仿真方法来验证其正确性. 分别研究了只一面作用气动载荷及两面同时受不同动压的气动载荷的薄壁板受斜激波冲击时的热气动弹性稳定性,给出了使壁板发生气动弹性失稳的边界条件. 得到以下结论：

(1)不论是只一面受气动载荷还是两面同时受不同动压的气动载荷作用,当壁板受激波作用时更容易发生热气动弹性失稳,并且随着激波强度的增大,受热壁板的稳定性也越来越差,极限环幅值和频率增大.

(2)当激波强度较小时,气动弹性稳定性边界仍将“壁温/动压”平面(图3(a))分成4个区域：渐进稳定区、屈曲区、基本型颤振区和过渡稳定区,但是随着激波强度的增大,壁板的临界屈曲温升减小;当激波强度更大时,气动弹性稳定性边界将平面的四个区域进一步分成5个部分,连续的渐进稳定区被屈曲区隔开成为两部分,并且即使温升为零时受热壁板也会发生屈曲.

(3)对于单面受气动载荷并且有激波作用的壁板,只有在激波前后的动压都满足稳定性边界条件下,壁板才可能保持气动弹性稳定性;对于双面受气动载荷并且一侧有激波作用的壁板,只有在激波前后的动压以及另一侧的动压都满足稳定性边界的条件下,壁板才可能保持气动弹性稳定性.

(4)与单面受气动载荷的情况相比,在两面受气动载荷的情况中,气动弹性稳定性边界对于激波强度的变化敏感度降低;在温升不变的情况下,气动弹性临界稳定动压会随着激波强度的增大而明显减小;在温升较小时,气动弹性临界稳定动压的增量随着温升的增大而减小,而当温升较大时,气动弹性临界稳定动压的增量保持不变.

(5)壁板上壁面的激波强度确定时,下壁面不同的超音速气流对气动弹性稳定性边界有影响;随着下壁面超音速气流的无量纲动压越大,受激波作用的受热壁板稳定性也越来越差,但临界屈曲温升在增大.

The authors have declared that no competing interests exist.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]	Xiao DY, Tian JY, Wei Z, et al. Damping effect on supersonic panel flutter of composite plate with viscoelastic mid-layer .Composite Structures, 2016, 137: 105-113 [本文引用: 1]
[2]	杨超,李国曙,万志强. 气动热--气动弹性双向耦合的高超声速曲面壁板颤振分析方法 . 中国科学:技术科学, 2012, 42(4): 369-377 [本文引用: 2] (Yang Chao, Li Guoshu, Wan Zhiqiang. Aerothermal-aeroelastic two-way coupling method for hypersonic curved panel flutter .Sci China Tech Sci, 2012, 42(4): 369-377 (in Chinese)) [本文引用: 2]
[3]	Jordan PF. The physical nature of panel flutter, Aero Digest, 1956: 34-38 [本文引用: 1]
[4]	Dowell EH. Nonlinear oscillations of a fluttering plate . AIAA Journal, 1966, 4: 1267-1275 [本文引用: 2]
[5]	Dowell EH. Nonlinear oscillations of a fluttering plate .AIAA Journal, 1967, 5: 1856-1862 [本文引用: 1]
[6]	Dowell EH. Panel flutter: A review of the aeroelastic stability of plates and shells .AIAA Journal, 1970, 8(3): 385-399 [本文引用: 1]
[7]	Cheng GF, Mei C. Finite element modal formulation for hypersonic panel flutter analysis with thermal effects .AIAA Journal, 2004, 42(4): 687-695 [本文引用: 1]
[8]	Bolotin VV, Petrovsky AV. Secondary bifurcations and global instability of an aeroelastic non-linear system in the divergence domain .Journal of Sound and Vibration, 1966, 191(3): 431-451 [本文引用: 1]
[9]	夏巍,杨智春. 超音速气流中受热壁板的稳定性分析 . 力学学报, 2007, 39(5):602-609 [本文引用: 5] (Xia Wei, Yang Zhichun. Stability analysis of heated panel in supersonic flows .Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(5): 602-609 (in Chinese)) [本文引用: 5]
[10]	Epureanu BI, Tang LS, Paidoussis MP. Coherent structures and their influence on the dynamics of aeroelastic panels .International Journal of Non-Linear Mechanics, 2004, 39: 977-991 [本文引用: 1]
[11]	Shiryayev OV, Slater JC. Aeroelastic system identification using the minimum model error method .Journal of Guidance, Control and Dynamics, 2006, 29(4): 936-943 [本文引用: 1]
[12]	Olson MD. Some flutter solutions using finite elements .AIAA Journal, 1970, 8(4): 747-752 [本文引用: 1]
[13]	Gray FE. Mei C. Finite element method for large-amplitude two-dimensional panel flutter at hypersonic speeds .AIAA Journal, 1991, 29: 411-488 [本文引用: 1]
[14]	Azzouz MS, Mei C.Nonlinear flutter of cylindrical panels under yawed supersonic flow using finite elements. AIAA 2005-2373, 2005 [本文引用: 1]
[15]	夏巍,杨智春,谷迎松. 超声速气流中受热壁板二次失稳型颤振 . 航空学报, 2009, 30(10): 1851-1856 [本文引用: 1] (Xia Wei, Yang Zhichun, Gu Yingsong. Secondary instability flutter of heated panels in supersonic airflow . Acta Aeronautica Et Astronautica Sinica, 2009, 30(10): 1851-1856 (in Chinese)) [本文引用: 1]
[16]	杨智春,夏巍,张蕊丽. 温度分布对复合材料壁板颤振特性的影响 . 宇航学报, 2010, 31(3): 850-854 [本文引用: 1] (Yang Zhichun, Xia Wei, Zhang Ruili. Effects of temperature distribution on panel flutter of composite plate . Journal of Astronautics, 2010, 31(3): 850-854 (in Chinese)) [本文引用: 1]
[17]	叶献辉,杨翊仁,肖艳. 热环境下三维壁板大气紊流动力响应分析 . 工程力学, 2009, 26(6): 233-237 [本文引用: 1] (Ye Xianhui, Yang Yiren, Xiao Yan. Dynamic response of three-dimensional panel with thermal effect to atmosphere turbulence .Engineering Mechanics, 2009, 26(6): 233-237 (in Chinese)) [本文引用: 1]
[18]	赵海,曹登庆,龙钢. 基于动态吸振器的高超声速复合材料壁板颤振抑制及其优化设计 . 航空动力学报, 2013, 28(10): 2202-2208 [本文引用: 1] (Zhao Hai, Cao Dengqing, Long Gang. Suppression of supersonic flutter of laminated composite panel using dynamic absorber device and its optimal design .Journal of Aerospace Power, 2013, 28(10): 2202-2208 (in Chinese)) [本文引用: 1]
[19]	周建,杨智春,谷迎松. 两面受气动载荷的壁板热弹性稳定性分析 . 中国科学:技术科学, 2012, 42(12): 1416-1422 [本文引用: 4] (Zhou Jian, Yang Zhichun, Gu Yingsong. Aeroelastic stability analysis of heated panel with aerodynamic loading on both surface .Sci China Tech Sci, 2012, 42(12): 1416-1422 (in Chinese)) [本文引用: 4]
[20]	叶坤,叶正寅, 屈展等. 高超声速舵面热气动弹性不确定性及全局灵敏度分析 . 力学学报, 2016, 48(2): 278-289 [本文引用: 1] (Ye Kun, Ye Zhengyin, Qu Zhan, et al. Uncertainty and global sensitivity analysis of hypersonic control surface aerothermoelastic .Chinese Journal of Theoretical and Applied Mechanics, 2016, 48(2): 278-289 (in Chinese)) [本文引用: 1]
[21]	刘成,叶正寅,叶坤. 转捩位置对全动舵面热气动弹性的影响 . 力学学报, 2017, 49(4): 802-810 [本文引用: 1] (Liu Cheng, Ye Zhengyin, Ye Kun. The effect of transition location on aerothermoelasticity of a hypersonic in all-movable centrol surface .Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(4): 802-810 (in Chinese)) [本文引用: 1]
[22]	张子健,刘云峰,姜宗林. 振动激发对高超声速气动力/热影响 . 力学学报, 2017, 49(3): 616-626 [本文引用: 1] (Zhang Zijian, Liu Yunfeng, Jiang Zonglin. Effect of vibration excitation on hypersonic aerodynamic and aerothermodynamic .Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(3): 616-626 (in Chinese)) [本文引用: 1]
[23]	Brouwer KR, Crowell AR, McNamara JJ. Rapid prediction of unsteady eoelastic loadsin shock-dominated flows//56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2015 [本文引用: 3]
[24]	Visbal MR. On the interaction of an oblique shock with a flexible Panel .Journal of Fluids and Structures, 2012, 30: 219-225 [本文引用: 1]
[25]	Visbal MR. Viscous and inviscid interactions of an oblique shock with a flexible panel .Journal of Fluids and Structures, 2014, 48: 27-45 [本文引用: 1]
[26]	Yao C, Zhang GH, Xu FC, et al. Influence of wall vibration on the aero performance of transonic diffuser//22nd AIAA Computational Fluid Dynamics Conference, 2015 [本文引用: 1]

Damping effect on supersonic panel flutter of composite plate with viscoelastic mid-layer

2016

... 壁板颤振是飞行器表面蒙皮在气动力、惯性力和弹性力的耦合作用下而发生的一种自激振动. 这种自激振动的发生是由于气流中的能量转移到了壁板中^[1]. 如果气流仅作用在壁板的一个面上,则称之为经典壁板颤振. 壁板颤振振动的幅值一般受到结构非线性的限制不会引发迅速的破坏,而更多的是造成结构的疲劳损伤. 虽然不同于机翼颤振一定会导致严重的飞行事故,但是剧烈的壁板颤振将会对壁板结构的疲劳寿命甚至飞行器的飞行性能产生不利的影响^[2]. ...

气动热--气动弹性双向耦合的高超声速曲面壁板颤振分析方法

2012

... 国内在壁板颤振方面也做了大量的工作. 夏巍等^[15]发现了二次失稳型颤振这种新的动态失稳现象,并研究了气流速压、壁板温升和初始扰动等因素对壁板的二次失稳型颤振特性的影响. 杨智春等^[16]研究了不同温度分布对复合材料壁板的颤振临界速压和非线性极限环颤振幅值的影响. 叶献辉等^[17]基于活塞流理论,研究了热环境下壁板大气紊流的动力响应特性,并分析了来流平均动压、温度、紊流强度及紊流尺度等参数对壁板结构均方根响应值的影响. 杨超等^[2]建立了气动热、气动弹性双向耦合高超声速二维曲面壁板颤振分析方法,发现基于这种双向耦合的壁板分析结果更加危险. 赵海等^[18]利用3阶非线性活塞理论进行气动力建模,研究了动态吸振器对高超声速流中复合材料壁板颤振的抑制作用. 上述研究都是针对壁板只一个表面受气流作用影响. 周建等^[19]通过解析分析和数值计算的手段研究了两面受气动载荷的壁板的热气动弹性稳定性,结果表明壁板两面同时作用气动载荷时更容易发生颤振失稳. ...

气动热--气动弹性双向耦合的高超声速曲面壁板颤振分析方法

2012

The physical nature of panel flutter,

1956

... Jordan ^[3]最早发现壁板颤振现象,他认为大量V-2火箭在早期试验中失效,是因为火箭头部的壁板发生了颤振. 然而,对壁板颤振进行系统的研究始于20世纪50年代^[4,5]. Dowell ^[6]全面综述了前人在壁板颤振分析所做的工作,根据结构是线性还是非线性以及所使用的气动力理论进行了分类. Cheng等^[7]在Dowell的基础上,将分析模型扩展到六类,并总结了各种气动力理论适用的马赫数范围. 20世纪60年代,Dowell ^[4]采用Von-Karman 板理论和一阶活塞理论,基于伽辽金法建立了二维壁板的气动弹性模型,成为壁板颤振研究中的一个经典案例. 由于该模型具有简单的数学表达式,许多研究者基于该模型进行了壁板颤振的机理研究^[8,9],并且发展了壁板颤振模型的降阶方法^[10]和数值分析方法^[11]. Olson ^[12]发展了用有限元方法来研究壁板颤振问题,为分析任意形状、载荷条件和边界条件的壁板振动提供了可能. Gray等^[13]分析了复合材料壁板的非线性颤振,并提出了频域内求解壁板的非线性颤振方程的LUM/NTF降阶方法. Azzouz等^[14]对受气流偏角影响的壁板颤振进行了分析,并研究了有气流偏角的二维和三维柱状壁板结构的非线性颤振特性. ...

Nonlinear oscillations of a fluttering plate

1966

... [4]采用Von-Karman 板理论和一阶活塞理论,基于伽辽金法建立了二维壁板的气动弹性模型,成为壁板颤振研究中的一个经典案例. 由于该模型具有简单的数学表达式,许多研究者基于该模型进行了壁板颤振的机理研究^[8,9],并且发展了壁板颤振模型的降阶方法^[10]和数值分析方法^[11]. Olson ^[12]发展了用有限元方法来研究壁板颤振问题,为分析任意形状、载荷条件和边界条件的壁板振动提供了可能. Gray等^[13]分析了复合材料壁板的非线性颤振,并提出了频域内求解壁板的非线性颤振方程的LUM/NTF降阶方法. Azzouz等^[14]对受气流偏角影响的壁板颤振进行了分析,并研究了有气流偏角的二维和三维柱状壁板结构的非线性颤振特性. ...

Nonlinear oscillations of a fluttering plate

1967

Panel flutter: A review of the aeroelastic stability of plates and shells

1970

Finite element modal formulation for hypersonic panel flutter analysis with thermal effects

2004

Secondary bifurcations and global instability of an aeroelastic non-linear system in the divergence domain

1966

超音速气流中受热壁板的稳定性分析

2007

... 式(12)为推导出的壁板在激波主导流动下的状态空间方程,将其与其他文献结果对比以验证其结果正确性. 将

λ_{u, l} = λ_{u, r}

代入上式中,即为无激波但壁板两面存在不同动压流场的情况,得到结果与文献[19]推导结果一致. 将

λ_{u, l} = λ_{u, r}

λ_{d} = 0

代入上式,即为经典壁板颤振情况,得到结果与文献[9]结果一致. ...

... 由于壁板的材料密度比相对空气密度要大得多,因此质量参数

R_{Mu, l}, R_{Mu, r}, R_{Md}

都是很小的值,并且从文献[9]的研究结论可知,质量参数对壁板稳定边界影响很小,在壁板颤振稳定性边界特性分析中可以忽略,因此可以由判别式(17c)得到保守解 ...

... 式(19)

~

式(21)和式(24)共同确定了上侧有激波主导的流场,下侧有超音速气流流过的受热壁板颤振稳定性边界.

n = 1

表示不考虑激波的影响,

m = 0

表示不考虑壁板下表面的超音速气流作用. 文献[19]中推导出了没有激波存在但双面受超音速气流作用的受热壁板的稳定性边界,将

n = 1

m λ_{u, l} = λ_{d}

代入上式中得到稳定性边界并与其比较,可见结果与文献[19]的结果完全一致. 文献[9]中推导出了单面受气动载荷的壁板颤振稳定性,将

n = 1

m = 0

代入上式中得到的结果与文献[9]的结果比较,结果完全一致. ...

... 代入上式中得到的结果与文献[9]的结果比较,结果完全一致. ...

超音速气流中受热壁板的稳定性分析

2007

... 式(12)为推导出的壁板在激波主导流动下的状态空间方程,将其与其他文献结果对比以验证其结果正确性. 将

λ_{u, l} = λ_{u, r}

代入上式中,即为无激波但壁板两面存在不同动压流场的情况,得到结果与文献[19]推导结果一致. 将

λ_{u, l} = λ_{u, r}

λ_{d} = 0

代入上式,即为经典壁板颤振情况,得到结果与文献[9]结果一致. ...

... 由于壁板的材料密度比相对空气密度要大得多,因此质量参数

R_{Mu, l}, R_{Mu, r}, R_{Md}

... 式(19)

~

式(21)和式(24)共同确定了上侧有激波主导的流场,下侧有超音速气流流过的受热壁板颤振稳定性边界.

n = 1

表示不考虑激波的影响,

m = 0

表示不考虑壁板下表面的超音速气流作用. 文献[19]中推导出了没有激波存在但双面受超音速气流作用的受热壁板的稳定性边界,将

n = 1

m λ_{u, l} = λ_{d}

代入上式中得到稳定性边界并与其比较,可见结果与文献[19]的结果完全一致. 文献[9]中推导出了单面受气动载荷的壁板颤振稳定性,将

n = 1

m = 0

代入上式中得到的结果与文献[9]的结果比较,结果完全一致. ...

... 代入上式中得到的结果与文献[9]的结果比较,结果完全一致. ...

Coherent structures and their influence on the dynamics of aeroelastic panels

2004

Aeroelastic system identification using the minimum model error method

2006

Some flutter solutions using finite elements

1970

Finite element method for large-amplitude two-dimensional panel flutter at hypersonic speeds

1991

超声速气流中受热壁板二次失稳型颤振

2009

超声速气流中受热壁板二次失稳型颤振

2009

温度分布对复合材料壁板颤振特性的影响

2010

温度分布对复合材料壁板颤振特性的影响

2010

热环境下三维壁板大气紊流动力响应分析

2009

热环境下三维壁板大气紊流动力响应分析

2009

基于动态吸振器的高超声速复合材料壁板颤振抑制及其优化设计

2013

基于动态吸振器的高超声速复合材料壁板颤振抑制及其优化设计

2013

两面受气动载荷的壁板热弹性稳定性分析

2012

... 式(12)为推导出的壁板在激波主导流动下的状态空间方程,将其与其他文献结果对比以验证其结果正确性. 将

λ_{u, l} = λ_{u, r}

代入上式中,即为无激波但壁板两面存在不同动压流场的情况,得到结果与文献[19]推导结果一致. 将

λ_{u, l} = λ_{u, r}

λ_{d} = 0

代入上式,即为经典壁板颤振情况,得到结果与文献[9]结果一致. ...

... 式(19)

~

式(21)和式(24)共同确定了上侧有激波主导的流场,下侧有超音速气流流过的受热壁板颤振稳定性边界.

n = 1

表示不考虑激波的影响,

m = 0

表示不考虑壁板下表面的超音速气流作用. 文献[19]中推导出了没有激波存在但双面受超音速气流作用的受热壁板的稳定性边界,将

n = 1

m λ_{u, l} = λ_{d}

代入上式中得到稳定性边界并与其比较,可见结果与文献[19]的结果完全一致. 文献[9]中推导出了单面受气动载荷的壁板颤振稳定性,将

n = 1

m = 0

代入上式中得到的结果与文献[9]的结果比较,结果完全一致. ...

... 代入上式中得到稳定性边界并与其比较,可见结果与文献[19]的结果完全一致. 文献[9]中推导出了单面受气动载荷的壁板颤振稳定性,将

n = 1

m = 0

代入上式中得到的结果与文献[9]的结果比较,结果完全一致. ...

两面受气动载荷的壁板热弹性稳定性分析

2012

... 式(12)为推导出的壁板在激波主导流动下的状态空间方程,将其与其他文献结果对比以验证其结果正确性. 将

λ_{u, l} = λ_{u, r}

代入上式中,即为无激波但壁板两面存在不同动压流场的情况,得到结果与文献[19]推导结果一致. 将

λ_{u, l} = λ_{u, r}

λ_{d} = 0

代入上式,即为经典壁板颤振情况,得到结果与文献[9]结果一致. ...

... 式(19)

~

式(21)和式(24)共同确定了上侧有激波主导的流场,下侧有超音速气流流过的受热壁板颤振稳定性边界.

n = 1

表示不考虑激波的影响,

m = 0

表示不考虑壁板下表面的超音速气流作用. 文献[19]中推导出了没有激波存在但双面受超音速气流作用的受热壁板的稳定性边界,将

n = 1

m λ_{u, l} = λ_{d}

代入上式中得到稳定性边界并与其比较,可见结果与文献[19]的结果完全一致. 文献[9]中推导出了单面受气动载荷的壁板颤振稳定性,将

n = 1

m = 0

代入上式中得到的结果与文献[9]的结果比较,结果完全一致. ...

... 代入上式中得到稳定性边界并与其比较,可见结果与文献[19]的结果完全一致. 文献[9]中推导出了单面受气动载荷的壁板颤振稳定性,将

n = 1

m = 0

代入上式中得到的结果与文献[9]的结果比较,结果完全一致. ...

高超声速舵面热气动弹性不确定性及全局灵敏度分析

2016

... 对于超声速和高超声速飞行器而言^[20,21],不同部件之间存在着多体干扰问题,一个部件的激波会作用在其他部件的壁面上^[22];在发动机的流道内部,流场中也存在复杂的波系;这些现象的共同之处就是激波主导下的壁面颤振问题,因此研究激波作用的流场中薄壁板的热气动弹性问题很有必要^[23]. 目前国内外已有学者对此问题展开研究,Visbal ^[24]通过完全可压缩的N-S方程来求解变形壁板上的无黏流场,从数值的角度研究了二维弹性壁板在激波作用下的动力学特性,结果表明当激波强度较大时,临界颤振动压远小于没有激波作用时壁板的临界颤振动压,稳定性明显降低. Visbal ^[25]在2014年进一步通过求解Euler和N-S方程研究了无黏和黏性流场中受激波作用的二维壁板的气动弹性,并分析激波位置对稳定性的影响. Brouwer等^[23]提出了用当地活塞流理论来预测有激波作用的流场中气动力的可行性. Yao等^[26]通过完全流固耦合(FSI)方法研究了壁面振动对跨音速扩散段中的气动力的影响. 然而,上述的研究也都是从数值角度进行分析,不能够得到系统参数间的定性规律,并且也只针对壁板只一面受气动荷载的情况. 目前从公开发表的文献看,还没有学者从解析理论的角度,研究斜激波作用下壁板的热气动弹性稳定性. ...

高超声速舵面热气动弹性不确定性及全局灵敏度分析

2016

转捩位置对全动舵面热气动弹性的影响

2017

转捩位置对全动舵面热气动弹性的影响

2017

振动激发对高超声速气动力/热影响

2017

振动激发对高超声速气动力/热影响

2017

McNamara JJ. Rapid prediction of unsteady eoelastic loadsin shock-dominated flows//56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics,

2015

... [23]提出了用当地活塞流理论来预测有激波作用的流场中气动力的可行性. Yao等^[26]通过完全流固耦合(FSI)方法研究了壁面振动对跨音速扩散段中的气动力的影响. 然而,上述的研究也都是从数值角度进行分析,不能够得到系统参数间的定性规律,并且也只针对壁板只一面受气动荷载的情况. 目前从公开发表的文献看,还没有学者从解析理论的角度,研究斜激波作用下壁板的热气动弹性稳定性. ...

... 为了有效预测激波主导流场中的气动力,采用当地一阶活塞流理论,文献[23]已经证实当地活塞流理论预测激波主导流场下气动力的可行性. 在当地活塞流理论中,相应的自由来流流动参数用当地参数来代替, 得到壁板上、下表面的气动力分别如下. ...

On the interaction of an oblique shock with a flexible Panel

2012

Viscous and inviscid interactions of an oblique shock with a flexible panel

2014

Influence of wall vibration on the aero performance of transonic diffuser//22nd

2015

〈

〉

激波主导流动下壁板的热气动弹性稳定性理论分析

AEROELASTIC STABILITY ANALYSIS OF HEATED FLEXIBLE PANEL IN SHOCK-DOMINATED FLOWS

引言

1 壁板在激波主导流动下的运动方程

2 壁板热颤振稳定性的解析分析

3 激波强度对壁板稳定性的影响

3.1 解析分析

3.2 数值仿真

4 壁板下壁面超音速气流对稳定性的影响

5 结论

参考文献 文献选项 原文顺序 文献年度倒序 文中引用次数倒序 被引期刊影响因子

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子