不同剪切率来流作用下柔性圆柱涡激振动数值模拟
天津大学水利安全与仿真国家重点实验室,天津 300072
Numerical simulation of vortex-induced vibration of a flexible cylinder exposed to shear flow at different shear rates
中图分类号: P751,TB531
文献标识码: A
通讯作者:
收稿日期: 2017-06-15
接受日期: 2017-09-30
网络出版日期: 2018-02-20
版权声明: 2018 《力学学报》编辑部 《力学学报》编辑部 所有
基金资助:
作者简介:
作者简介:及春宁(1978―),男,河北人,教授,博士,主要从事流固耦合、涡激振动、泥沙运动研究(E-mail: cnji@tju.edu.cn)
展开
摘要
采用浸入边界法对细长柔性圆柱在线性剪切流条件下的涡激振动进行三维数值模拟。细长柔性圆柱振动采用三维索模型模拟,其两端铰接,质量比为6,长细比为50,无量纲顶张力为496。来流为线性剪切流,剪切率从0到0.024变化,最大雷诺数为250。研究发现:剪切流作用下柔性立管横流向振动表现为驻波模式,而顺流向振动表现为行波-驻波混合模式。随着剪切率增大,振动频谱呈现多频响应,振动能量逐渐向低频转移。阻力系数平均值随着展向变化,脉动阻力系数和升力系数的均方根值均表现为“双峰”模式。流固能量传递系数沿立管轴向的分布表明,振动激励区集中于高流速区,而振动阻尼区多位于低流速区。剪切率较小时,圆柱的泻涡为平行交叉模式;剪切率较大时,圆柱的泻涡为倾斜泻涡模式,且由于泻涡频率沿立管轴向变化,尾流发生涡裂现象,形成泻涡频率不同的胞格结构。
关键词:
Abstract
In this paper, the immersed boundary method was used to simulate the vortex-induced vibration of a slender flexible cylinder exposed to linear shear flows. The vibration of the cylinder was simulated by using a three-dimensional cable model pinned at both ends. The cylinder has a mass ratio of 6 and an aspect ratio of 50. The normalized top tension is 496. The incoming flow has different linear velocity profiles with the shear rates ranging from 0 to 0.024. The maximum Reynold number is 250. It was found that the transverse vibration shows a standing wave pattern while the streamwise vibration shows a combined traveling-standing wave pattern. With the increase of the shear rate, the distribution of Power Spectrum Density (PSD) of vibration responses shows a multi-frequency mode, and the vibration energy shifts to low frequency bands. The mean drag coefficient varies in the spanwise direction while the root-mean-square (RMS) values of fluctuating drag and lift coefficients show a two-peak pattern. The distribution of the fluid-solid energy transferring coefficient indicates that the vibration-exciting region coincides with the high-velocity region while the vibration-damping region matches the low-velocity region. For the cases with low shear rates, the vortex-shedding behind the cylinder shows the interwoven pattern. However, for the cases with large shear rates, the vortex-shedding displays the oblique pattern. Due to the spanwise variation of the vortex-shedding frequency, the vortex-splitting occurs in the near-wake, leading to the vortex cells with different vortex-shedding frequencies.
Keywords:
引言
细长柔性海洋立管受海流作用,两侧交替地产生脱离结构物表面的旋涡,这种交替泻涡会在立管上生成顺流向及横流向周期性变化的脉动压力,引发涡激振动现象,从而易导致结构疲劳损坏。实际海洋环境中,水流条件复杂多变,立管不仅受正交均匀流的作用,更多情况下还受到倾斜流、剪切流、阶梯流等作用。当前,对正交均匀来流情况下的细长柔性圆柱涡激振动的研究[1]较为充分,而对剪切流作用下的相关研究较少。
Newman和Karniadakis[2]数值模拟了长细比为100的柔性圆柱在剪切流中的横流向振动,发现振动模式为行波-驻波混合响应模式。Lucor[3]进行了长细比大于500、雷诺数为1000的柔性圆柱涡激振动低分辨率直接数值模拟,发现在线性剪切流中,高流速区存在锁定区域。Lucor等[4]研究认为对于柔性圆柱横流向振动,指数剪切流速剖面比线性剪切流速剖面会产生更大的振动频率带宽。但和实际情况相比,圆柱单自由度振动的研究具有一定局限性。
Lie和Kaasen[5]开展了剪切流作用下的物理模型实验,立管的长细比高达3000。Vandiver等[6]对细长柔性立管涡激振动进行了现场测量,发现柔性立管表现出多模态激励,在高模态下行波占主导。
Bourguet等[7,8,9,10]通过直接数值模拟方法研究了不同雷诺数下剪切来流中的柔性立管涡激振动。发现圆柱振动同时包含行波和驻波的混合振动模式,沿立管展向不同区域分别按照一定的频率进行泻涡,区域之间易发生尾涡分裂(vortex splitting)。
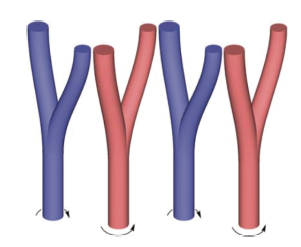
对于在均匀流中的长圆锥形柱,Techet和Hover[11]、Flemming和Williamson[12]指出,由于涡分裂,出现了沿展向不同的泻涡模式,即:2S和2P模式组成的混合泻涡模式,如图1所示。
国内学者也开展了卓有成效的研究。陈伟民等[13]研究了立管的预张力、流场分布等参数对涡激振动响应和附加质量的影响。发现:模态锁频区域的大小与立管张力有关,各阶模态振幅随其单调增大。唐国强等[14]进行了长细比为1750的柔性立管多模态涡激振动特性研究,认为:柔性立管涡激振动中,除了主导模态外,其他模态贡献较小,但会造成沿空间分布的不对称性以及相位差。
宋磊建等[15]在大型水池中设置可绕中心轴做圆周运动的T型塔架,开展了线性剪切流中立管涡激振动的实验研究。高云等[16]通过旋转臂架形成相对剪切来流,开展了长细比为225、质量比为3.3的柔性圆柱涡激振动实验。
对于阶梯状来流剖面,姚宗等[17]在拖曳水池中设计了流速增大装置,实验研究了阶梯来流中细长柔性立管的涡激振动。郭海燕等[18]开展了内流作用下长细比为310的立管在阶梯来流中的涡激振动实验,并与尾流振子模型的结果进行了比较。
大长细比柔性圆柱涡激振动数值模拟对计算资源要求较高,当前国内外对圆柱涡激振动的研究主要开展二维模拟或采用切片法开展准三维模拟,而运用三维直接数值模拟方法开展的相关研究比较少。
本文采用基于浸入边界法的高效并行计算程序CgLes_IBM开展了不同剪切率来流下细长柔性圆柱涡激振动的三维数值模拟,克服切片方法的不足,可以得到更加真实的流场和振动响应。
1 数值方法与验证
1.1数值方法
本文应用基于浸入边界法(Immersed Boundary Method)的三维水动力并行计算程序CgLES_IBM,并结合隐式结构动力计算程序X-Code,对倾斜来流作用的柔性立管涡激振动开展了数值模拟研究。
流体运动的数值模拟的控制方程如下
$\frac{\partial \mathbf{u}}{\partial t}=-\text{(}\mathbf{u}\cdot \mathsf{\nabla }\text{)}\mathbf{u}-\mathsf{\nabla }p+\text{ }\!\!\nu\!\!\text{ }{{\mathsf{\nabla }}^{2}}\mathbf{u}+\mathbf{f}$ (1)
$\mathsf{\nabla }\cdot \mathbf{u}=0$ (2)
其中,$\mathbf{u}$为速度,$t$为时间,$p$为压强,$\nu$为运动粘滞系数, $\mathsf{\nabla }$为梯度算子,$\mathbf{f}$为附加体积力矢量,代表流固耦合边界条件。
对以上控制方程采用二阶精度的Adams-Bashforth时间格式进行离散,可得控制方程的守恒形式如下
$\begin{align} {{\mathbf{u}}^{n+1}}={{\mathbf{u}}^{n}}+\delta t\text{(}\frac{3}{2}{{h}^{n}}-\frac{1}{2}{{h}^{n-1}} -\frac{3}{2}\mathsf{\nabla }{{p}^{n}}+\frac{1}{2}\mathsf{\nabla }{{p}^{n-1}}\text{)}+{{\mathbf{f}}^{n+\frac{1}{2}}}\delta t \end{align}$ (3)
$\mathsf{\nabla }\cdot {{\mathbf{u}}^{n+1}}=0$ (4)
其中,$h=\mathsf{\nabla }\cdot \text{(}-\mathbf{uu}+\nu \text{(}\nabla \mathbf{u}+\nabla {{\mathbf{u}}^{\text{T}}}\text{))}$由对流项与扩散项组成,上标$\text{T}$为矩阵转置,附加体积力表示为
$\begin{align} {{\mathbf{f}}^{n+\frac{1}{2}}}\delta t=D\text{(}{{\mathbf{V}}^{n+1}}-\operatorname{I}\text{(}{{u}^{n}}+\;\delta t\text{(}\frac{3}{2}{{h}^{n}} -\frac{1}{2}{{h}^{n-1}}-\frac{3}{2}\mathsf{\nabla }{{p}^{n}}+\frac{1}{2}\mathsf{\nabla }{{p}^{n-1}}\text{)))} \\ \end{align}$ (5)
式中,$I$和$D$为插值函数,${{V}^{n+1}}$为物面边界的速度,上标$n+1$, $n+1/2$, $n$, $n-1$为时间步。
针对传统浸入边界法施加边界条件精度不高的情况,Ji[19]等提出了基于嵌入式迭代的浸入边界法,将浸入边界法嵌入到压力泊松方程的迭代求解中,利用压强的中间解比初始值更接近真实值的特点,迭代修正附加体积力,在不显著增加额外计算耗时的前提下,提高整个算法的求解精度。
将柔性立管简化为两端铰接的弹性索。采用有限元法求解弹性索的动力平衡方程,表示为
$\mathbf{M}{{\ddot{\zeta}}_{\text{ }\!\!\{\!\!\text{ }x,y\text{ }\!\!\}\!\!\text{ }}}-\mathbf{T}\zeta _{\text{ }\!\!\{\!\!\text{ }x,y\text{ }\!\!\}\!\!\text{ }}^{''}+\mathbf{K}{{\dot{\zeta }}_{\text{ }\!\!\{\!\!\text{ }x,y\text{ }\!\!\}\!\!\text{ }}}=\frac{{{C}_{\text{ }\!\!\{\!\!\text{ }x,y\text{ }\!\!\}\!\!\text{ }}}}{2}$ (6)
其中,$M$为集中质量矩阵,$I$为刚度矩阵,$K$为阻尼矩阵,$C_\{x,y\}$为顺流向和横流向流体力系数,$\zeta _\{x,y\}$为振动位移,$\cdot $和$'$代表对时间和空间的导数。
本文采用三维二结点索单元对结构进行空间离散,每个结点具有3个自由度。结构动力方程采用$\text{Newmark-}\beta $法进行求解,该方法为无条件稳定,具有二阶时间精度,时间步长的取值可以灵活地与流场的时间步长协调一致。
1.2 验证算例
为了验证数值模拟方法的求解精度,本文将其应用于圆柱绕流问题的数值模拟中,并与其他结果进行对比。圆柱绕流是十分经典的流体力学问题,很多学者通过数值模拟和模型实验等方法开展了详细的研究。本文对三维刚性圆柱绕流进行了数值模拟,圆柱长细比为L/D=10,雷诺数为Re=1000。
表1 条件下圆柱绕流结果对比
Table 1 Comparison of flow around a circular cylinder with $Re=1000$
| $L/D$ | $-{{C}_{pb}}$ | ${{\bar{C}}_{D}}$ | $C_{L}^{'}$ | $St$ | |
|---|---|---|---|---|---|
| Consequence | 10 | 0.82 | 1.02 | 0.20 | 0.215 |
| Tong, et al[20] | 10 | 0.90 | 1.09 | 0.20 | 0.215 |
| Naito, et al[21] | 2π | 0.92 | 1.09 | 0.21 | 0.210 |
表1给出圆柱下游侧压强$-{{C}_{pb}}$、平均阻力系数${{\bar{C}}_{D}}$、脉动升力系数$C_{L}^{'}$、泻涡频率数$St$,并与Tong等[20]和Naito等[21]的数模结果进行了对比。可见,本文结果与已有结果比较接近,验证了本文方法的准确性。
除了圆柱绕流[22,23]验证外,本文还针对圆柱涡激振动进行了模拟,并与Prasanth 和 Mittal[24]的结果进行了对比。模拟参数设置为:雷诺数$\operatorname{Re}=100$,折合流速${{U}_{r}}=6$,圆柱质量比$m=10$。表2给出了横流向振幅${{y}_{\max }}/D$、顺流向平均位移$\bar{x}/D$、平均阻力系数${{\bar{C}}_{D}}$、脉动升力系数$C_{L}^{'}$和泻涡频率$St$的对比。可以发现,两者差异不超过2%,再次证明本文方法具有较高精度。
表2 $Re=100$条件下圆柱涡激振动结果对比
Table 2 Comparison of vortex-induced vibration of a circular cylinder with $Re=100$
| ${{y}_{\max }}/D$ | $\bar{x}/D$ | ${{\bar{C}}_{D}}$ | $C_{L}^{'}$ | $St$ | |
|---|---|---|---|---|---|
| Consequence | 0.522 | 0.1119 | 1.91 | 0.1554 | 0.1636 |
| Prasanth Mittal [24] | 0.516 | 0.1110 | 1.90 | 0.1571 | 0.1644 |
| Error (%) | 1.16 | 0.81 | 0.53 | 1.08 | 0.49 |
1.3 数值模拟设置
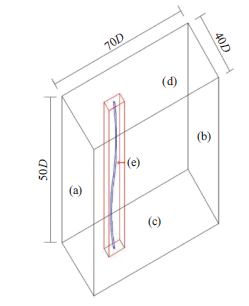
流体计算域为长方体,$x$、$y$和$z$方向的尺寸分别为$70D$(顺流向)、$40D$(横流向)和$50D$(展向),如图1所示。初始状态下,立管中心距入流边界$20D$,距出流边界$50D$,距侧边界均为$20D$。
边界条件为:入流边界为Dirichlet型边界,出流边界为Neumann型边界,横流向为可滑移边界,圆柱表面为无滑移边界,上下端为周期性边界。无量纲时间步长为$\Delta tD/{{U}_{\max }}=0.002$。
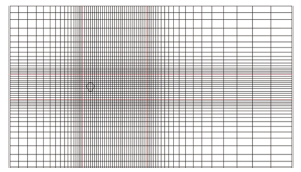
在$x-y$平面内,采用非均匀正交网格对计算域进行空间离散,如图2所示。为提高精度,在圆柱附近进行加密。加密区的尺寸为$16D\times 6D$,加密区内采用均匀正交网格,网格边长为$D/32$。加密区以外采用渐变网格,网格边长以指数形式增长。展向采用均匀网格,共划分192层。
来流为线性剪切流,其剪切率定义为$\mathrm{ }\!\!\beta\!\!\text{ }=\text{(}1/{{U}_{avg}}\text{)}\partial {{U}_{l}}/\partial z$。其中,${{U}_{avg}}$是入流流速剖面的平均速度,$\partial {{U}_{l}}/\partial z$为流速剖面的斜率。采用四个速度剖面,即$\mathrm{ }\!\!\beta\!\!\text{ =}$0、0.0057、0.013和0.024。其中,$\mathrm{ }\!\!\beta\!\!\text{ }=0$对应均匀来流的情况。来流边界上最大流速为${{U}_{\max }}=2.5$,位于$z=0$处,对应的雷诺数为${{\operatorname{Re}}_{\max }}=250$。最小流速为${{U}_{\min }}=$2.5、1.875、1.25和0.625,位于$z=50D$处,对应的雷诺数分别为${{\operatorname{Re}}_{\min }}=$250、187.5、125和62.5。
细长柔性圆柱两端铰接,直径为$D$,长度$L$为$50D$,质量比$m={{\mathrm{ }\!\!\rho\!\!\text{ }}_{c}}/{{\mathrm{ }\!\!\rho\!\!\text{ }}_{f}}{{D}^{2}}=6$。其中,${{\mathrm{ }\!\!\rho\!\!\text{ }}_{c}}$为单位长度圆柱的质量,${{\mathrm{ }\!\!\rho\!\!\text{ }}_{f}}$为流体的密度。
在圆柱两端施加无量纲顶张力$T=\mathrm{ }\!\!\tau\!\!\text{ }/{{\mathrm{ }\!\!\rho\!\!\text{ }}_{f}}{{D}^{2}}U_{\max }^{2}=496$。其中,$\mathrm{ }\!\!\tau\!\!\text{ }$为顶张力,沿立管展向不变。圆柱振动的无量纲相速度为$\mathrm{ }\!\!\omega\!\!\text{ }=\sqrt{T/m}\approx 9.09$,真空中无量纲固有频率为${{f}_{i,v}}=\mathrm{ }\!\!\omega\!\!\text{ }/{{\mathrm{ }\!\!\lambda\!\!\text{ }}_{i}}$。其中,${{\mathrm{ }\!\!\lambda\!\!\text{ }}_{i}}$为无量纲波长,对于一阶和二阶阵型来说,${{\mathrm{ }\!\!\lambda\!\!\text{ }}_{1}}=100$,${{\mathrm{ }\!\!\lambda\!\!\text{ }}_{2}}=50$。相应地,一阶和二阶无量纲固有频率分别为${{f}_{1}}=0.091$和${{f}_{2}}=0.182$。考虑到$\operatorname{Re}=$250情况下静止圆柱的泻涡频率为$St\approx 0.19$,与${{f}_{2}}$接近,圆柱横流向振动将主要表现为二阶模态。
图 2 计算域和边界条件^(a) Dirichlet 型边界条件, (b) Neumann 型边界条件, (c) 可滑移边界, (d) 周期边界, (e) 无滑移边界
Fig. 2 Computational domain and boundary conditions^(a) Dirichlet BC, (b) Neumann BC, (c) free-slip BC, (d) periodic BC, (e) no-slip BC
2 结果与分析:
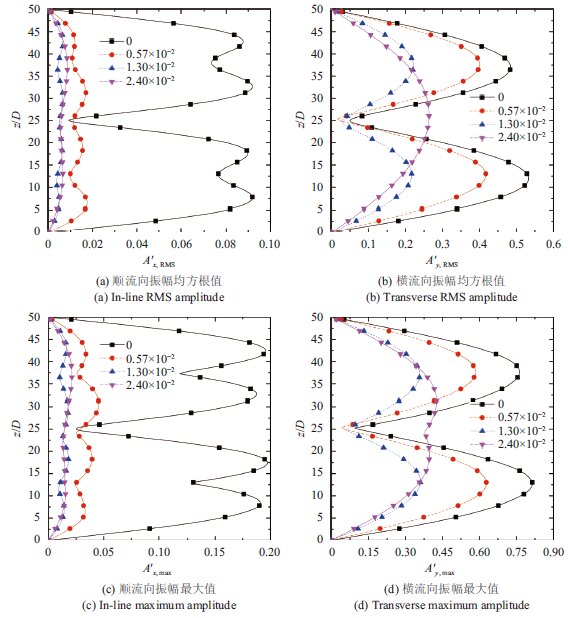
图4给出了四种不同剪切率工况下圆柱的顺流向和横流向振幅的均方根值和最大值。其中,顺流向振幅扣除了时均位移。可以看出:剪切率为0、0.0057和0.013工况下,顺流向呈现四阶振型(剪切率为0时,顺流向为二阶、四阶共存),横流向呈现二阶振型。并且,随着剪切率的增大,振幅逐渐减小。剪切率为0.024工况下,顺流向呈现二阶振型,横流向则为一阶振型(略显二阶振型)。
可以发现:随着剪切率的增大,横流向和顺流向振型阶数逐渐降低,振幅的最大值和均方根逐渐减小。其主要原因在于,剪切流作用下,立管沿展向的无量纲固有频率是变化的。局部速度越大(小),该处无量纲顶张力越小(大)、无量纲固有频率越小(大)。例如,对于剪切率为0.013的情况,$z=0$处,圆柱的固有频率为${{f}_{1}}{{|}_{z=0}}=0.091$和${{f}_{2}}{{|}_{z=0}}=0.182$,$z=50D$处,圆柱的固有频率为${{f}_{1}}{{|}_{z=50D}}=0.182$和${{f}_{2}}{{|}_{z=50D}}=0.364$。
为了考察圆柱振动的平均固有频率,可采用平均来流速度${{U}_{avg}}$进行无量纲化,则四种剪切来流条件下,圆柱的一阶平均无量纲固有频率分别为0.091、0.104、0.121和0.145,二阶平均无量纲固有频率分别为0.182、0.208、0.242和0.291。
可见,$\beta =0$、0.0057和0.013工况下,圆柱的泻涡频率(st≈0.19)与二阶固有频率接近,因此横流向振动表现为二阶模态,但随着剪切率的增大,泻涡频率逐渐偏离二阶固有频率,因此振幅逐渐降低。β=0.024工况下,泻涡频率与一阶固有频率更接近,因此横流向振动表现为一阶模态,略显二阶阵型,振幅较小。一般情况下,顺流向振动的频率和模态为横流向振动的两倍。可以发现,随着剪切率的增大,平均流速降低,立管振动向低阶模态过渡,这与下文能量谱分析结论相印证。
图5为四种工况下圆柱涡激振动位移空间时程分布,横轴为无量纲时间,纵轴为无量纲展向坐标。$\beta =0$工况下,顺流向和横流向振动均表现为典型的“驻波”振动模式,横流向振型呈现二阶模态,顺流向则存在二阶和四阶振动模态。由于顺流向振动的二阶和四阶分量强度相当,因此其空间时间分布表现为正“Y”和倒“Y”交替出现的形式。$\beta =$0.0057工况下,横流向振动为“驻波”模式,二阶模态。顺流向振动表现为“行波驻波”混合模式,四阶模态占优。$\beta =$0.013工况下,横流向振动为“驻波”模式,二阶模态。顺流向振动四阶模态占优,同时存在一阶和三阶分量,“行波驻波”混合模式更加明显,行波所占比重增大。$\beta$=0.024工况下,横流向振动为“驻波”模式,一阶模态占优,存在二阶分量。顺流向振动较为混乱,以“行波”模式主导,二阶模态占优,同时存在较强的一阶和三阶分量。
图 5 圆柱涡激振动位移空间时程分布
Fig. 5 The space-time distribution of VIV displacement of a cylinder
可以看出,剪切率对振动响应的影响较为显著,随着剪切率逐渐增加,顺流向振动逐渐向“行波”模式变化,多频共存的现象逐渐明显。横流向振动主要为“驻波”模式,这与圆柱的长细比较小有关。
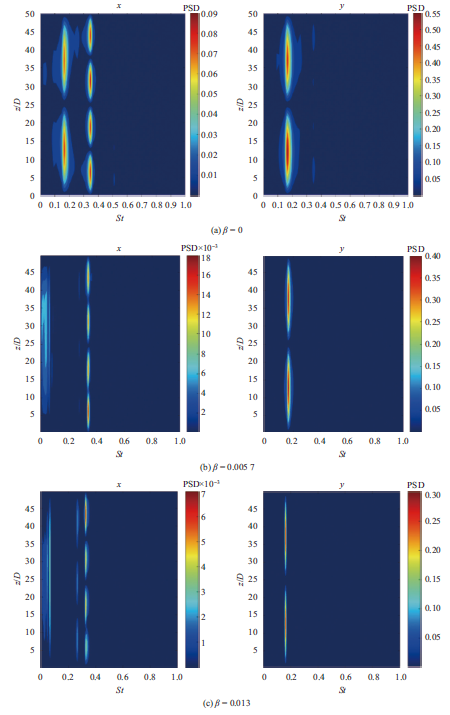
对各剪切率工况下圆柱两向振动进行能量谱密度分析,如图6所示。可以看出,$\beta =$0的工况下,横流向振动能量主要集中于二阶频率,顺流向振动能量则集中于二阶和四阶频率,且两者强度相当。$\beta =$0.0057 的工况下,横流向集中在二阶频率,顺流向集中在四阶频率,并且存在微弱的低频拍振频率。$\beta =$0.013工况下,横流向集中在二阶频率,而顺流向除了四阶频率外,还出现了一阶频率和三阶频率,但四阶频率的能量占优。$\beta =$0.024工况下,横流向出现了一阶和二阶频率,二阶频率占优,顺流向出现了一阶、二阶、三阶频率和拍振频率,能量集中于二阶频率上。可见,随着剪切率的增大,振动能量出现了由高频向低频过渡的趋势,尤其是顺流向振动更为明显。
图7为各工况下圆柱横流向振动波腹处的振动轨迹。可以看出,后三组工况的振动轨迹均能分辨出“8”字形,而$\beta =$0的工况中振动轨迹呈现出不规则的“O”形,这与$\beta =$0工况含有二阶和四阶横流向振动模态,且在波腹位置处二阶模态占优有关。此外,与均匀来流($\beta =$0)结果相比,剪切流作用下,由于“行波”模式的出现,振动轨迹不能相互重叠,振动的不稳定性较强。
图 8 流体力系数和流固能量传递系数
Fig. 8 Fluid force coefficient and fluid-solid energy transfer coefficient
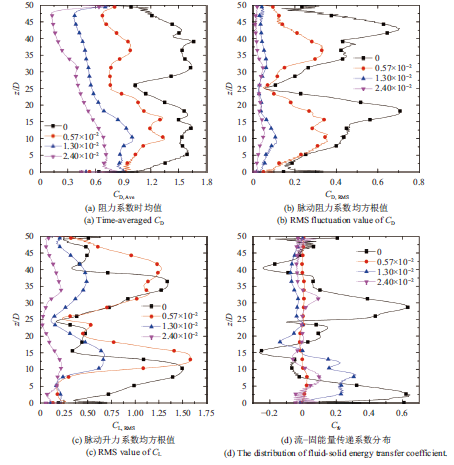
如图8(a)-(c)给出了不同剪切率条件下流体力系数沿展向的分布。总体来看,流体力系数随剪切率的增大而减小。随着展向高度的增大,阻力系数平均值总体上不断降低,这是由于流速剖面由下到上流速逐渐减小,从而圆柱上部阻力较小。然而,阻力系数平均值并非单调减小,而是存在一定幅度的波动。这主要是由于圆柱的涡激振动所致,振幅越大,时均阻力也越大。由于圆柱振幅沿展向变化,故阻力系数平均值出现波动。随着剪切率的增大,圆柱的振动逐渐减小,阻力系数平均值的波动幅度也相应减小。
因圆柱横流向振动对流体力值起主导作用,由图4(b)可以看出,横流向振幅均方根值沿圆柱展向表现为二阶振动模态,故脉动阻力系数和脉动升力系数的均方根值均表现为“双峰”模式。对于大剪切率$\beta =$0.024工况,结合图6(d),虽然横流向振幅均方根值为一阶模态占优,但二阶模态的存在造成脉动升阻力产生两个峰值。
流固能量传递系数是表征流固耦合系统的非线性平衡态的重要参数,可以用来认识流固之间能量传递的时空特性,对VIV现象的机理解释具有明显的理论意义。时均流固能量传递系数定义为
${{C}_{fv}}(z)=\frac{\frac{2}{{{T}_{s}}}\int_{{{T}_{s}}}{({{{\tilde{C}}}_{d}}(z,t){{{\dot{\tilde{A}}}}_{x}}(z,t)+{{C}_{l}}(z,t){{{\dot{A}}}_{y}}(z,t))dt}}{\sqrt{\frac{2}{{{T}_{s}}}\int_{{{T}_{s}}}{(\dot{A}_{x}^{2}(z,t)+\dot{A}_{y}^{2}(z,t))}dt}}$ (7)
其中,${{\tilde{C}}_{d}}$和${{C}_{l}}$为脉动阻力系数,${{\dot{\tilde{A}}}_{x}}$和${{\dot{A}}_{y}}$代表立管顺流向和横流向振动速度,${{T}_{s}}$为统计时间,取整数倍的振动周期。${{C}_{fv}}$是各展向位置能量转移的参数,用来量化流体对圆柱做功的功率。${{C}_{fv}}$为正值代表流体向结构提供能量,圆柱振动处于激发状态,而${{C}_{fv}}$为负值表明流体耗散结构的振动能量,圆柱振动处于阻尼状态。
图8(d)给出了不同剪切率工况下流固能量传递系数沿展向的变化关系。剪切流工况下,流固能量传递系数变化呈现一个共同特点,即流速大的区域为能量输入区,流速小的区域为能量阻尼区,这与Bourguet[8]在大长细比立管涡激振动研究中得到的结果相一致。在剪切流的作用下,立管展向的泻涡频率会出现“漂移”或“迁移”现象,能量阻尼区(非锁定区域)存在于较大的展向范围内,且随着剪切率的增大而增大。
图9给出了不同剪切率下的圆柱泻涡过程。可见,均匀流工况下,圆柱的泻涡为平行交叉模式(interwoven vortex shedding pattern),与圆柱的“驻波”振动模式对应。而剪切流工况下,圆柱的泻涡为倾斜泻涡模式(oblique vortex shedding pattern),与圆柱的“行波”振动模式对应。倾斜偏向低流速区域,且角度随着剪切率的增大而增大。尾涡的倾斜剥离“驱动”着圆柱振动中的行波分量不断从高流速区域向低流速区域传播。可见,倾斜泻涡的方向和振动行波分量的行进方向之间具有联系。
此外,剪切来流下圆柱泻涡较为复杂,存在明显的三维特性。尾流易形成不同频率涡核组成的胞格结构(cellular pattern)[25,26],胞格结构间出现涡旋错位(vortex dislocation)或者涡分裂现象(vortex splitting)[27,28]。
如图9(c)、(d)红色方框中所示,大剪切率工况中可以观察到涡分裂现象。$\beta =$0.013的工况在展向高度z=30~37.5范围内发生尾涡分裂,$\beta =$0.024工况在展向高度z=15附近发生尾涡分裂。这是由于局部流速不同,泻涡频率沿展向发生变化。由于泻涡沿展向具有连续性,泻涡频率可在一定长度内保持稳定。当泻涡频率的变化积累到一定程度时,尾涡发生分裂,以适应局部泻涡频率,形成泻涡频率不同的胞格结构。胞格结构内部为倾斜泻涡,胞格结构之间,尾涡通过涡丝(vortex filaments)保持连续。
3 结论
采用浸入边界法对细长柔性圆柱在线性剪切流条件下的涡激振动进行了三维数值模拟。细长柔性圆柱采用两端铰接的弹性索模型,圆柱的长细比为50,质量比为6,无量纲顶张力为496,雷诺数为250。采用四个速度剖面,即剪切率为0、0.0057、0.013和0.024,研究了圆柱的振动模态、频率、振幅、能量谱、振动轨迹、流体力、流固能量传递系数和泻涡模式等,得到结论如下:
(1).随着剪切率的增大,顺流向振动从二、四阶模态共存过渡到多阶(一、二、三阶)模态共存,横流向振动从二阶模态过渡到一阶模态占优。此外,随着剪切率的增大,顺流向振动逐渐向“行波”模式变化,多频共存的现象逐渐明显;横流向振动主要为“驻波”模式,这与圆柱的长细比较小有关。
(2).随着剪切率的增大,振动能量出现了由高频向低频过渡的趋势,尤其是顺流向振动更为明显。
(3).均匀流工况的振动轨迹呈现出不规则的“O”形,剪切流工况的振动轨迹呈现出“8”字形。剪切流作用下,由于“行波”模式的出现,振动轨迹不能相互重叠,振动的不稳定性强。
(4).平均阻力系数随着展向高度的增大不断降低,脉动阻力系数和升力系数的均方根值均表现为“双峰”模式,剪切流工况下,上部的峰值比下面的略小。
(5).剪切流工况下,流固能量传递系数变化呈现共同特点,即流速大的区域为能量输入区,流速小的区域为能量阻尼区。
(6).均匀流工况下,泻涡模式为平行交叉模式,与圆柱的“驻波”振动模式对应;而剪切流工况下,泻涡模式为倾斜泻涡模式,与圆柱的“行波”振动模式对应。大剪切率工况中观察到了涡分裂现象,形成泻涡频率不同的胞格结构。胞格结构之间,尾涡通过涡丝保持连续。
The authors have declared that no competing interests exist.
参考文献
| [1] |
柔性圆柱涡激振动流体力系数识别及其特性 .Identification and characteristics of hydrodynamic coefficients for a flexible cylinder undergoing vortex-induced vibration . |
| [2] |
A direct numerical simulation study of flow past a freely vibrating cable . |
| [3] |
Vortex dislocations and force distribution of long flexible cylinders subjected to sheared flows . |
| [4] |
Riser modal identification in CFD and full-scale experiments . |
| [5] |
Modal analysis of measurements from a large-scale VIV model test of a riser in linearly sheared flow . |
| [6] |
Insights on vortex-induced, traveling waves on long risers . |
| [7] |
Multi-frequency vortex-induced vibrations of a long tensioned beam in linear and exponential shear flows . |
| [8] |
Distributed lock-in drives broadband vortex-induced vibrations of a long flexible cylinder in shear flow . |
| [9] |
Vortex-induced vibrations of a long flexible cylinder in shear flow . |
| [10] |
Mono- and multi- frequency vortex-induced vibrations of a long tensioned beam in shear flow . |
| [11] |
Vortical patterns behind a tapered cylinder oscillating transversely to a uniform flow . |
| [12] |
Vortex-induced vibrations of a pivoted cylinder . |
| [13] |
采用改进尾流振子模型的柔性海洋立管的涡激振动响应分析 .Prediction of vortex-induced vibration of flexible riser using improved wake-oscillator model . |
| [14] |
大长细比柔性杆件涡激振动实验 .Laboratory measurement of vortex-induced vibration of long flexible riser . |
| [15] |
剪切流下发生涡激振动的柔性立管阻力特性研究 .Investigation Of Drag Forces For Flexible Risers undergoing Vortex-Induced Vibration In Sheared Flow . |
| [16] |
剪切来流下柔性圆柱体涡激振动响应试验研究 .Experimental study on vortex induced vibration responses of a flexible cylinder in sheared current . |
| [17] |
流速分层流场中细长柔性立管涡激振动试验研究 .Experimental Investigation on Vortex Induced Vibration of a Long Flexible Riser in a Stepped Current . |
| [18] |
海洋立管涡激振动模型的实验验证 .Comparisons of Numerical Simulation and Experimental Study on Vortex-Induced Vibration of Marine Riser Under Stepped Current . |
| [19] |
A novel iterative direct-forcing immersed boundary method and its finite volume applications . |
| [20] |
Numerical simulations of steady flow past two cylinders in staggered arrangements . |
| [21] |
Control of flow around a circular cylinder for minimizing energy dissipation . |
| [22] |
串列双圆柱流致振动的数值模拟及其耦合机制 .Numerical investigation on flow-induced vibration of two cylinders in tandem arrangements and its coupling mechanisms . |
| [23] |
并列双圆柱流致振动的不对称振动和对称性迟滞研究 .Numerical investigation on the asymmetric vibration and symmetry hysteresis of flow-induced vibration of two side-by-side cylinders . |
| [24] |
Vortex-induced vibrations of a circular cylinder at low Reynolds numbers . |
| [25] |
An experimental study of vortex shedding behind linearly tapered cylinders at low Reynolds number . |
| [26] |
Szepessy S et al. Experiments on the flow past long circular cylinders in a shear flow . |
| [27] |
The natural and forced formation of spot-like ‘vortex dislocations’ in the trasition of a wake . |
| [28] |
Oblique and parallel modes of vortex shedding in the wake of a circular cylinder at low Reynolds numbers . |

/
| 〈 |
|
〉 |