引言
轮轨黏着力是指车轮与钢轨在滚动接触时的切向力,是列车牵引和制动的主要动力,直接关系到列车运行的安全性、舒适性. 最 大黏着力与摩擦力有关,摩擦力的减小会导致黏着力的减小. 当轮轨间无液体(雨水、油污) 或固体(沙粒、树叶、锈) 等第三介质,并且处于直线段平稳运行时,黏着系数变化不大. 然而,日本新干线实测数据显示,对于湿润状态的轮轨接触,特别是列车运行速度超过200 km/h,黏着系数将显著下 降[1-3 ] . 这是因为:(1) 车轮与钢轨的接触区域可分为固体接触区和液体接触区,轮轨黏着力由这两个区域共同提供,与没有液体 时的情况相比,部分固体接触区域被液体隔开,而液体的剪切力远小于固体接触剪切力,因此,总的剪切力低于全部为固 体接触时的剪切力;(2) 水的黏度很低,对于高弹性模量材料(如:钢) 的高压接触,如果速度不是很大,例如:列车运行 在120 km/h 以下,水的润滑作用可以忽略,只有速度非常大,其流体动压效应才能形成一定厚度的水膜,从而体现出润滑作用. 早在20 世纪80 年代,Ohyama 等[4-7 ] 利用小尺度双盘对滚实验装置系统地研究了水、液态石蜡等液体介质存在 时,最高运动速度为200 km/h 的轮轨黏着系数与速度的演变关系. 在20 世纪90 年代,Zhang 等[8 ] 利用1:1 轮对滚动振动试验台研究了最高运动速度为280 km/h 时水润滑黏着系数与速度的 演变关系,得到的结论 是随着速度的增大,黏着系数不断减小. 对于速度更高的情况,以及轴重、温度等其他条件也变化的情况,如果都用实验研究,既不经济,有时也难以实施. 因此,利用数学模型,进行数值分析,研究轮轨黏着系数随速度、温度等因素的变化规律,可为实验研究和现场测试提供 重要的参考依据.
关于水润滑轮轨接触研究的数学模型除了文献[9 ,10 ] 用界面流体模型以外,绝大多数研究者都采用基于雷诺方程的弹流 润滑(elasto-hydrodynamic lubrication, EHL) 模型[11 ] . 由于求解雷诺方程十分困难,通常采用Grubin 提出的近似解或数值解法[12 ] . Chen 等[13 ] 将轮轨接触简化为线接触,用Grubin 解首次计算了与轮轨表面粗糙度相关的、运动速度达300 km/h 的黏 着系数与速度的演变关系. 平均流量模型是Patir 提出的另一种求解雷诺方程的方法[14 ] ,该方法假设流经接触区的流量是恒定的,即:设定平均流量因子$\Phi_x$, $\Phi_y$,并利用参数$\gamma$表征表面形貌取向($\gamma <1$表示横纹, $\gamma =1$表示均匀形貌, $\gamma >1$表示纵纹,这种表征方法也称为随机模型). 该方法可求解与表面形貌取向相关的弹流润滑问题[15 ] . Chen 等[16 -17 ] 用该方法研究了表面粗糙度及其取向对水润滑轮轨黏着系数的影响规律. Wu 等[18 -20 ] 把平均流量模型推广到弹塑性接触并考虑接触热效应,给出了最高运动速度为350 km/h 时, 黏着系数与速度之间的关系. 文献[17 ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用.
本文采用文献[25 ] 提出的统一雷诺方程模型计算水润滑轮轨接触问题,该模型的核心思想是:当液膜或间隙为零 时,利用退化的雷诺方程可以求解干接触问题. 因此,对固体接触区和液体接触区都用雷诺方程求解,从而避免了确定固体区与液体区边界条件所带来的困难. 在形貌方面,以实测的表面形貌为基础,以拟合的形貌函数为输入文件. 在文献[22 ] 的基础上,将统一雷诺方程模型用于计算车轮表面具有宏观规则形貌的水润滑高速轮轨接触,研究表面 形貌取向、黏着系数及运动速度的之间关系.
1 分析模型
根据统一雷诺方程模型, 求解混合弹流润滑问题的方程为
∂ ∂ x ρ h 3 12 η ∂ p ∂ x + ∂ ∂ y ρ h 3 12 η ∂ p ∂ y = u ∂ ( ρ h ) ∂ x + ∂ ( ρ h ) ∂ t
其中$x$ 轴方向与运动方向相同, $\eta $ 为液体的黏度,$u=(u_{1}+u_{2})/2$,$u_{1}$, $u_{2}$ 分别为两运动表面的切向速度,$h$ 为膜厚或接触面的间隙,它与时间和位置有关,由如下方程表示
h ( x , y , t ) = h 0 ( t ) + x 2 2 R x + y 2 2 R y + δ 1 ( x , y , t ) + δ 2 ( x , y , t ) + v ( x , y , t )
式中$h_{0}(t)$ 为接触面无变形时的初始间隙,将车轮等效为圆柱体,径向半径为$R_{1x}$,轴向半径$R_{1y}=\infty$,钢轨等效为半径$R_{2y}$ 的弧形曲面的无限长直体,即:$R_{2x}=\infty$,$R_{x}$ 和$R_{y}$ 为当量主曲率半径,$\dfrac{1}{R_x } = \dfrac{1}{R_{1x} } +\dfrac{1}{R_{2x} }$,$\dfrac{1}{R_y } = \dfrac{1}{R_{1y} } + \dfrac{1}{R_{2y}}$, $\delta_{1}$ 和$\delta_{2}$ 分别为轮轨表面的初始粗糙度,$v(x, y, t)$为表面弹性变形量,表达式为
$v(x,y,t)=2E’\int \int_{\Gamma} p_{1}(x’,y’)+p_{s}(x’,y’) \sqrt{(x-x’)^{2}+(y-y’)^{2} }dx’dy’$ (3)
其中$p_{\rm l}$ 为流体动压,$p_{\rm s}$ 为固体接触压力,$E'$ 为当量弹性模量,$\varOmega $ 表示计算域. 流体动压可通过方程(1) $\sim$ 式(3) 联立求解.
对于固体接触区,$h=0$,方程(1) 简化为以下形式
u ∂ h ∂ x + ∂ h ∂ t = 0
对于稳态,方程(4) 可进一步简化为
∂ h ∂ x = 0 (5)
由于方程(5) 是方程(1) 的特殊形式,这样就可以通过求解一个方程组而得到整个接触区中的完全数值解. 在数值计算时,流体动压与固体接触压力都可以通过相同的循环迭代而求得,无需任何有关固体区与液体区边界及边界条件的信息. 该方法巧妙地避开了难以寻求的固液边界条件,极大地方便了求解域中压力与膜厚的计算.
水看作可压缩牛顿流体,方程(1) 中$\eta $代表水的黏压关系[26 ]
η = η 0 + η 1 p + η 2 p 2 + η 3 p 3 + η 4 p 4
式中,$\eta_{0}$ 为水的常温(20${^\circ}$C) 黏度, $\eta_{1}$, $\eta _{2}$, $\eta _{3}$, $\eta_{4}$ 采用陈桦等的拟合结果[13 ] . 水的密度按下式计算
ρ = ρ 0 ( 1 + 0.6 × 1 0 - 9 p 1 + 1.7 × 1 0 - 9 p )
混合润滑状态下,载荷由固体区与液体区共同承担,载荷平衡方程
p = P s + P l = ∫ ∫ Ω p s ( x , y ) d x d y + ∫ ∫ Ω p l ( x , y ) d x d y
其中$P_{\rm s}$ 和$P_{\rm l}$ 分别表示固体区和液体区的载荷,$p$ 为总载荷. 以上所有方程组成了一个非线性方程组,经离散化、无量纲化处理,并用离散卷积$\!$-$\!$-$\!$ 快速傅里叶变换和网格逐渐加密相结合的方法,迭代求解[27-28 ] .
黏着系数由下式给出
μ = μ s P s + μ l P l p
其中, $\mu_{\rm s}$ 是固体接触区的摩擦系数,它的大小由边界条件决定,一般由实验确定. 对于水的混合润滑,通常取0.14$\sim $0.45 之间的数值[16, 29 ] ,本文取0.2. $\mu _{\rm l}P_{\rml}$ 为液体接触区的剪切力,对于水润滑条件,剪切力满足如下牛顿流体形式[30 ]
γ ̇ = τη
其中$\dot {\gamma }$ 和$\tau $ 分别为水的剪应变率和剪应力.
2 数值模拟
在求解雷诺方程的迭代程序中,用$\varepsilon_{1}=1.00\times 10^{ -6}$,作为$h=0$ 的判断标准. 当无量纲膜厚$H=h/a$ 小于 $\varepsilon_{1}$ 时,认为膜厚为零,两表面接触,雷诺方程中的压力流动项关闭. 用另一个数$\varepsilon _{2}=1.00\times 10^{ - 5}$ 来检验$\partial h / \partial x$. 如果$H \le \varepsilon_{1}$ 和$\partial h / \partial x \le \varepsilon_{2}$同时成立,雷诺方程中的挤压项应去除. 总的来说,根据不同的$H$ 和$\partial h /\partial x$ 值,迭代程序将选择不同的方程进行计算,即 $ H > \varepsilon _1$: 使用方程(1);$ H \le \varepsilon _1$ 且$\partial h / \partial x > \varepsilon _2 $: 使用方程(4); $ H \le \varepsilon _{1}$ 且$\partial h / \partial x \le \varepsilon _2$: 使用方程(5). 数值模拟中,相关的数据参数如表1 所示(表中蠕滑率$s = (u_1 - u_2 ) / u\times 100\%$). 在点接触条件下,接触区为椭圆,由表1 中的相关数据计算得到最大赫兹接触压力为$p_{\rm h}=1.22$\,GPa,接触区椭圆参数分别为:长半轴$a=6.61$\,mm(运动方向),短半轴$b=5.04$\,mm(垂直于运动方向),相应地接触区椭圆率$k=b/a=0.76$。
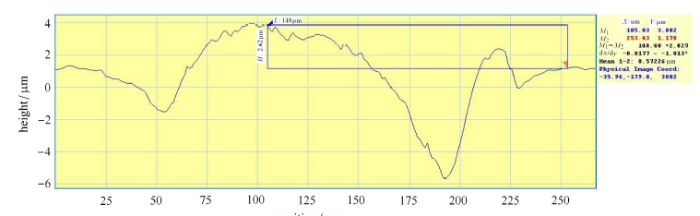
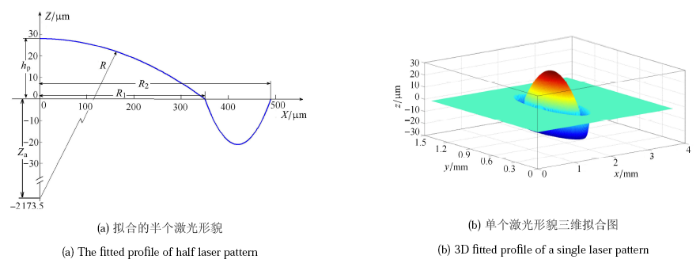
文献[22 ] 在小尺度试样表面制备了激光毛化形貌,单个激光毛化形貌的直径约为150 m,深度约为3 m (图1 ),这些单个激光形貌以400 m 和 200 m 的间距规则分布,形成纵纹、横纹、菱形三种宏观形貌. 由于高速列车车轮踏面的平均磨耗约为230 ~ 500 m 每10 万公里[31 ] ,从实际应用的角度考虑,本文将单个激光形貌及其分布按比例放大,构建车轮表面激光宏观规则 形貌,使单个激光形貌的直径约为1.0 mm. 图2 (a) 为采用二维分段函数拟合的半个激光形貌的纵剖面,函数表达式如下
$z(x,y)=\begin{equation} \left \{ \begin{array} \ \sqrt{R^2-x_{s}^{2}-y_{s}^{2}}-Z_{a}, \sqrt{x_{s}^{2}+y_{s}^{2}} \le R_{1} \\ A(\sqrt{x_{s}^{2}+y_{s}^{2}}-R_{1})(\sqrt{x_{s}^{2}+y_{s}^{2}}-R_{2}) \\ R_{1} < \sqrt{x_{s}^{2}+y_{s}^{2}} \le R_{2} \\ rand(z), else \end{array} \right. \end{equation} $ (11)
图1 单个激光形貌的实测纵剖面. 其直径约为150 m,粗糙峰高度2.5 m
Fig. 1 The real cross-section profile of a single laser pattern. The diameter of the pattern is about 150 m, the height over the surface is about 2.5 m
式(11) 的第1 部分表示球冠的局部,其中$R$,$R_{1}$,$R_{2}$,$Z_{\rm a}$,$A$,$h_{\rm p}$ 的说明由图2 (a) 给出. $Z_{\rm a}=R-h_{\rm p}$,$h_{\rm p}$ 表示粗糙峰的高度. 式(11) 的第2 部分是由三点拟合得到二次曲面方程. 第3 部分表示无激光形貌的区域,其粗糙度为$R_{\rm q}$. 在计算中,此区域的$R_{\rm q}$ 设为4.0\,$\upmu $m. 拟合得到的参数为$R=2\,201.5\,\upmu $m,$R_{\rm 1} =350\,\upmu $m,$R_{2}=490\,\upmu $m,$A=4.3\times 10^{ -3}$,$h_{\rm p}=28\,\upmu $m. 其中$x_{\rm s}$ 和 $y_{\rm s}$ 随不同分布而变化
x s = x - 2 800 n , y s = y - 2 800 n , rhombus pattern x s = x - 2 800 n , y s = y - 1 400 n , transverse pattern ( n is the number of iterations ) x s = x - 1 400 n , y s = y - 2 800 n , longitudinal pattern
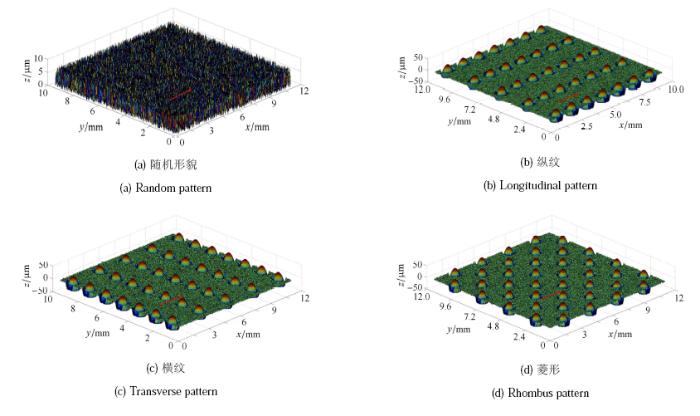
根据方程(11) 与(12),拟合得到的单个激光形貌立体图如图2 (b). 图3 是拟合得到的车轮表面激光宏观规则形貌.
图2 单个激光形貌的拟合轮廓
Fig. 2 The fitted profiles of laser pattern
图3 用于计算的重构表面. 箭头所指为运动方向
Fig. 3 The reconstructed surface for calculation. The arrows indicate the direction of rolling
将方程和边界条件无量纲化,设无量纲数$X=x/a$, $Y=y/b$, 求解域为$-3.0 \le X \le 2.1$ 和$-2.5 \le Y \le 2.5$,并将其划分为$192 \times 128$ 个等距网格,相应的网格间距为$\Delta X=0.026 562 5$, $\Delta Y=0.039 062 5$. 在计算不同速度与蠕滑率下的EHL 工况时都是以相应的光滑表面的数值解作为具有宏观规则形貌的初始值.
3 结果与讨论
3.1 压力与膜厚
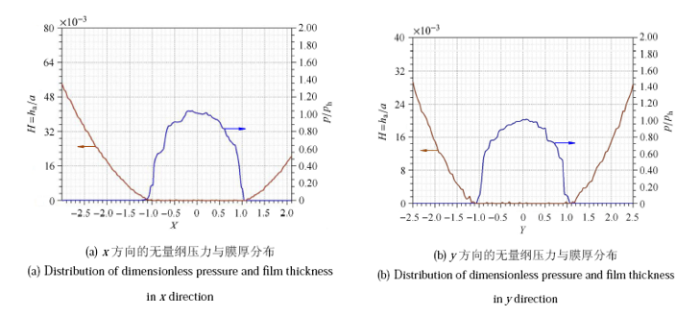
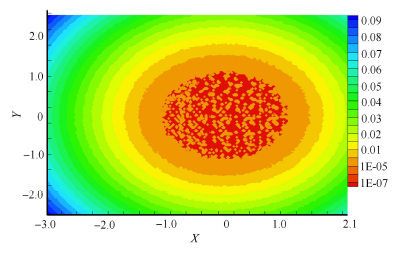
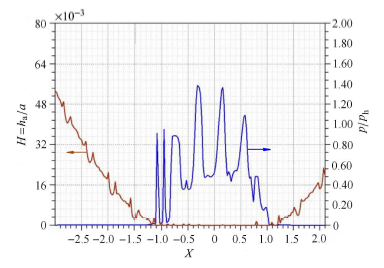
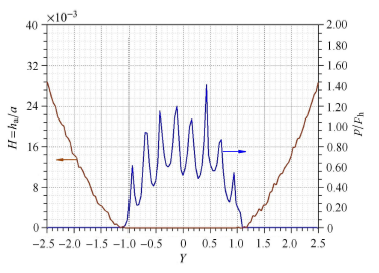
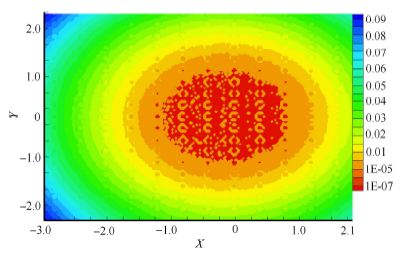
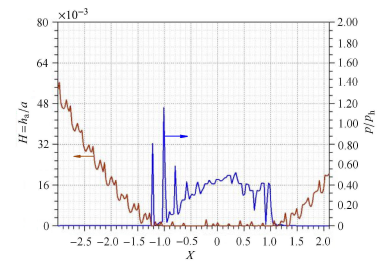
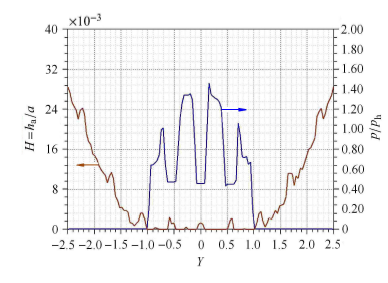
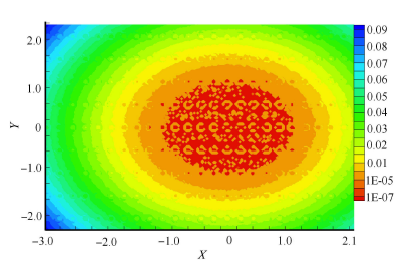
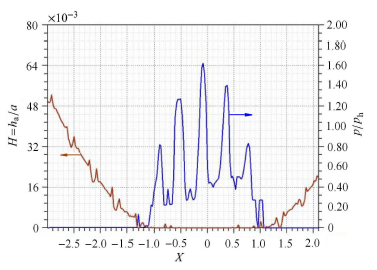
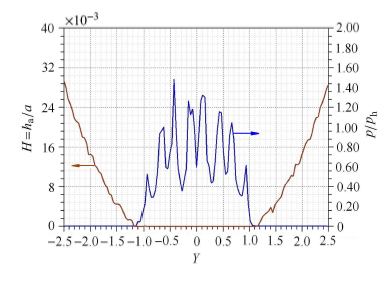
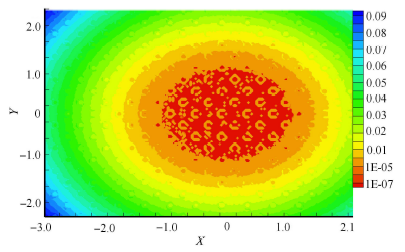
通过求解雷诺方程,得到具有规则形貌的车轮与钢轨接触时,接触区的压力与膜厚的分布. 图4 至图7 表示运动速度为300 km/h,蠕滑率为1.0%,具有随机形貌和横纹、纵纹、菱形形貌的车轮与钢轨接触时的压 力、膜厚分布. 其中,图4 ~图7 中的(a) 图和(b) 图分别为接触区中心线上的二维压力与膜厚分布(其中$h_a$为轮轨间的名义接触区内的平均膜厚或者平均间隙),图4 ~图7 中的(c) 图为接触区的膜厚云图.
从这些分布图可以看出:随机形貌的压力及膜厚分布无明显的波动,而具有规则形貌的压力及膜厚波动较为显著,这是 由于具有宏观规则形貌的微凸体会引起接触压力的剧烈波动,使车轮表面局部区域经历多次高应力冲击(图4 ~图7 ). 无 论是随机形貌还是三种特征形貌,在出口处都没有出现二次压力峰,而油润滑则存在明显的二次压力峰[22, 32 ] ,显然,这是因为水的黏度大约只有油的黏度的1/20 所造成的. 在具有规则形貌的膜厚云图中(图5 ~图7 中的(c)), 圆圈表示具有激光形貌的激光作用区,可以看出单个激光作用区由深红色和橘黄色两部分组成,其中深红色部分表示固体接 触(即 $H=h_{a}/ \alpha < 1.00 \times 10^{-6}$),橘黄色部分是液体接触区,说明激光毛化形貌的凹坑具有一定的润滑作用.
图4-1 随机形貌的无量纲压力、膜厚分布及膜厚云图(a) $x$ 方向的无量纲压力与膜厚分布 (b) $y$ 方向的无量纲压力与膜厚分布
Fig. 4-1 Distribution of dimensionless pressure and film thickness and dimensionless film thickness contour with random topography(a) Distribution of dimensionless pressure and film thickness in $x$ direction (b) Distribution of dimensionless pressure and film thickness in $y$ direction
图4-2 随机形貌的无量纲压力、膜厚分布及膜厚云图(c) 膜厚云图$H=h_{\rm a}/a$
Fig. 4-2 Distribution of dimensionless pressure and film thickness and dimensionless film thickness contour with random topography(c) Contour plot of film thickness $H=h_{\rm a}/a$
图5-1 横纹纹理的无量纲压力、膜厚分布及二维膜厚云图 (a) x 方向的无量纲压力与膜厚分布
Fig. 5-1 Distribution of dimensionless pressure and film thickness and dimensionless film thickness contour with transverse pattern (a) Distribution of dimensionless pressure and film thickness In x direction
图5-2 横纹纹理的无量纲压力、膜厚分布及二维膜厚云图 (b) y 方向的无量纲压力与膜厚分布
Fig. 5-2 Distribution of dimensionless pressure and film thickness and dimensionless film thickness contour with transverse pattern (b) Distribution of dimensionless pressure and film thickness in y direction
图5-3 横纹纹理的无量纲压力、膜厚分布及二维膜厚云图 (c) 膜厚云图$H=h_{\rm a}/a$
Fig. 5-3 Distribution of dimensionless pressure and film thickness and dimensionless film thickness contour with transverse pattern (c) Plot of film thickness $H=h_{\rm a}/a$
图6-1 纵纹纹理的无量纲压力、膜厚分布及二维膜厚云图 (a) $x$方向的无量纲压力与膜厚分布
Fig. 6-1 Distribution of dimensionless pressure and film thickness and dimensionless film thickness contour with longitudinal pattern (a) Distribution of dimensionless pressure and film thickness in $x$ direction
图6-2 纵纹纹理的无量纲压力、膜厚分布及二维膜厚云图 (b) $y$方向的无量纲压力与膜厚分布
Fig. 6-2 Distribution of dimensionless pressure and film thickness and dimensionless film thickness contour with longitudinal pattern (b) Distribution of dimensionless pressure and film thickness in $y$ direction
图6-3 纵纹纹理的无量纲压力、膜厚分布及二维膜厚云图 (c) 膜厚云图$H=h_{\rm a}/a$
Fig. 6-3 Distribution of dimensionless pressure and film thickness and dimensionless film thickness contour with longitudinal pattern (c) Contour plot of film thickness $H=h_{\rm a}/a$
图7-1 菱形纹理的无量纲压力、膜厚分布及二维膜厚云图 (a)$x$方向的无量纲压力与膜厚分布
Fig. 7-1 Distribution of dimensionless pressure and film thickness and dimensionless film thickness contour with rhombus pattern (a) Distribution of dimensionless pressure and film thickness in $x$ direction
图7-2 菱形纹理的无量纲压力、膜厚分布及二维膜厚云图 (b)$y$方向的无量纲压力与膜厚分布
Fig. 7-2 Distribution of dimensionless pressure and film thickness and dimensionless film thickness contour with rhombus pattern (b) Distribution of dimensionless pressure and film thickness in $y$ direction
图7-3 菱形纹理的无量纲压力、膜厚分布及二维膜厚云图 (c) 膜厚云图$H=h_{\rm a}/a$
Fig. 7-3 Distribution of dimensionless pressure and film thickness and dimensionless film thickness contour with rhombus pattern (c) Contour plot of film thickness H=h_{\rm a}/a$
3.2 表面形貌取向对黏着系数的影响
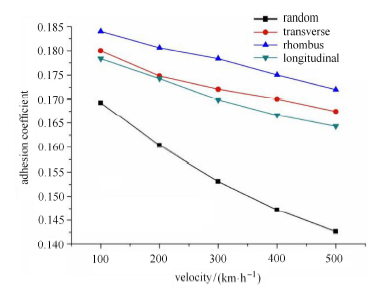
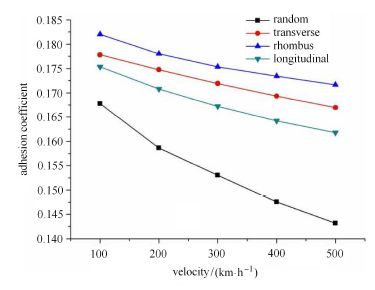
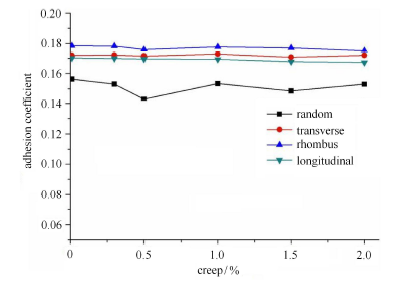
计算表明,(1) 在水润滑状态下,随机形貌以及纵纹、横纹、菱形对应的轮轨黏着系数都随速度的增大而降低(图8 和图9 只显示 蠕滑率分别为0.3% 和2.0% 的两情况). 这与油润滑或其他液体润滑的结果是一致的,即:流体动压随速度的增大而增大,膜厚增大,因而,黏着系数减小. (2) 蠕滑率$s$的变化对黏着系数的影响不大,如图10 (图中仅显示了300 km/h 时的情况). 这是因为本文的计算没有考虑接触摩擦热导致的温度的变化,这与文献[33 ] 的结果是一致的. 如果考虑接触摩擦热使轮轨接触区温度升高,则对应的黏着系数都减小[20 ] . 无论是干接触态还是润滑态,各种实验结果都显示,当蠕滑率增大到一定程度时,黏着系数有一个峰值,过了峰值之后, 黏着系数将随蠕滑率的增大而减小[34 -38 ] . 因为在实验中,接触摩擦热是必定存在的.
当运动速度较低时,譬如,速度为100 km/h,3 种规则形貌的黏着系数相差不大. 但是,当速度超过200 km/h,3 种规 则形貌的黏着系数明显大于随机形貌的黏着系数. 这说明,激光规则形貌可有效提高水润滑轮轨黏着系数. 特别值得注意的是,计算结果表明菱形的黏着系数大于横纹的黏着系数,而纵纹的黏着系数又小于横纹的. 这与平均流量模型的计算结果正好相反[17 -20 ] ,而与高速轮轨水润滑黏着系数的实验结果相符[21 ] .
关于表面形貌取向对黏着系数的影响,存在不同的、甚至是相互矛盾的研究结果. Akbarzadeh 根据从Jeffreys 方程推导出的Moes 模型计算得到的结果是:横纹的黏着系数大于纵纹的黏着系 数[39 -42 ] . 这个模拟方法既没有设定接触区的形状,也没有“流量恒定” 这个假设. Zhu 等[43 ] 用统一雷诺方程模型系统地研究了从线接触到点接触、从低速到高速、从边界润滑到全膜润滑的各种情 况下表面形貌取向对膜厚比($\gamma$) 的影响规律,结论是:在混合润滑条件下($0.05 < \gamma < 1.0$),对于线接触和点接触椭圆率$k > 1$的情况,侧流效应可忽略,因而,横纹的膜厚比大于纵纹的膜厚比,相当于横纹 黏着系数小于纵纹黏着系数;对于点接触椭圆率$k < 1$的情况,侧流效应不能忽略,因而,纵纹的膜厚比大于横纹的膜厚比,相当于纵纹黏着系数小于横纹黏着系数. 这说明,平均流量模型所假设的接触区流量恒定只对于线接触和点接触中椭圆率$k \gg 1$的情况适用,对于$k \ll 1$和$k \approx 1$的情况,平均流量模型可能导致谬误.
图8 黏着系数随速度的变化曲线($s=0.30\%$)
Fig.8 The adhesion coefficient with various speeds at the creep rate of 0.30%
图9 黏着系数随速度的变化曲线($s=2.0\%$)
Fig. 9 The adhesion coefficient with various speeds at the creep rate of 2.0%
图10 速度为300 km/h 黏着系数随蠕滑率的变化曲线
Fig. 10 The adhesion coefficient with various creep rates at the speed of 300 km/h
从物理上说,无论接触区形状如何,对于具有特定取向的表面形貌,横纹和菱形对来流的阻碍作用比纵纹大,导致液体流向接触 区外,即侧流效应较为显著. 相反,纵纹有利于液体通过接触区,侧流效应相对较弱,纵纹比横纹和菱形可形成更厚的水膜,因此,纵纹黏着系数较小. 只有在宽度大于长度的线接触中或椭圆率$k \gg 1$的点接触中,并且液体黏度较大时,才有可能出现侧流效应可忽略的情况,即Patir 所谓的宽轴承情况[15 ] ,使横纹对 来流的阻碍作用导致膜厚增大,黏着系数减小.
本文作者用统一雷诺方程模型研究了表面形貌取向对黏着系数的影响规律,对于油润滑、线接触,结论是[22 ] :$\mu_{\hbox{菱形}}> \mu_{\hbox{纵纹}}> \mu _{\hbox{横纹}}$,对于水润滑、$k<1$ 的点接触,结论是: $\mu_{\hbox{菱形}}> \mu_{\hbox{横纹}}> \mu_{\hbox{纵纹}}$. 这充分说明,关于表面形貌取向对黏着系数的影响规律不是一成不变的. 表面形貌取向、黏度、接触区形状等因素决定了接触区的流动状态,进而改变固体接触压力与总压力之比. 方程(9) 表明,在混合润滑状态下,影响黏着系数的主要原因是固体接触压力与总压力之比[17 ] . 表2 是速度为300 km/h,蠕滑率为1.0% 时,接触压力与总压力的比值. 可以看出比值的大小关系为,菱形大于横纹,横纹大于纵纹,而纵纹又大于随机形貌. 因此,黏着系数大小的顺序为:菱形的最大,横纹其次,纵纹次之,随机形貌的最小.
4 结论
本文以激光毛化形成的纵纹、横纹、菱形等规则形貌为基础,经过等比例放大、拟合,作为车轮表面形貌,用统一雷诺方程 模型计算了高速轮轨水润滑条件下,黏着系数随表面形貌取向及速度变化的结果,结论如下:
(1) 当蠕滑率一定并且运动速度超过200 km/h,三种规则形貌的轮轨黏着系数都随速度的增大而降低,其中菱形的黏着系数大于 横纹的黏着系数,横纹的黏着系数又大于纵纹的黏着系数.
(2) 在混合润滑条件下,平均流量模型只对某些形状的接触区适用,而统一雷诺方程模型可适用于任何形状的接触区,并且计算 结果物理意义明确、清晰.
(3) 影响黏着系数的主要原因是固体接触压力与总压力之比.
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
Ohyama T Tribological studies on adhesion phenomena between wheel and rail at high speed
.Wear , 1991 , 144 : 263 -275
[2]
杨国伟 , 魏宇杰 , 赵桂林 等 . 高速列车的关键力学问题
. 力学进展 , 2015 , 45 : 201507
Yang Guowei Wei Yujie Zhao Guilin et al .Research progress on the mechanics of high speed rails
.Advances in Mechanics , 2015 , 45 : 201507 (in Chinese)
[3]
翟婉明 , 金学松 , 赵永翔 . 高速铁路工程中若干典型力学问题
. 力学进展 , 2010 , 40 (3 ): 358 -374
Zhai Wanming Jin Xuesong Zhao Yongxiang Some typical mechanics problems in high-speed railway engineering
.Advances in Mechanics , 2010 , 40 (3 ): 358 -374 (in Chinese)
[4]
Ohyama T. Traction and slip at higher rolling speeds: Some experiments under dry friction water lubrication
//Kalousek J, editors. Contact Mechanics and Wear of Rail/Wheel Systems, Proceedings of the International Symposium held at the University of British Columbia , Vancouver : University of Waterloo Press , 1983 , 395 -418
[5]
Ohyama T Ohno K Nakano S Influence of surface contamination on adhesion force between wheel and rail at higher speeds-1st report-behavior of adhesion force under the surfaces contaminated with a small amount of liquid paraffin
.J Jpn Soc Lubr Eng , 1989 , 10 : 111 -114
[6]
Ohyama T Influence of surface contamination on adhesion force between wheel and rail at higher speeds-2nd Report-effects of friction coefficients and tangential rigidity on adhesion force
.J Jpn Soc Lubr Eng , 1989 , 10 : 115 -120
[7]
Ohyama T Nakano S Influence of surface contamination on adhesion force between wheel and rail at higher speeds-3rd Report-behavior of adhesion force under the formation of lubricant film
.J Jpn Soc Lubr Eng , 1989 , 10 : 121 -124
[8]
Zhang WH Chen JZ Wu XJ et al .Wheel/rail adhesion and analysis by using full scale roller rig,
Wear , 2002 , 253 : 82 -88
[本文引用: 1]
[9]
Tomberger C Dietmaier P Sextro W Friction in wheel-rail contact: A model comprising interfacial fluids, surface roughness and temperature
.Wear , 2011 , 271 (1-2 ): 2 -12
[本文引用: 1]
[10]
Zhu Y Olofsson U Söderberg A Adhesion modeling in the wheel-rail contact under dry and lubricated conditions using measured 3D surfaces
.Tribol Inter , 2013 , 61 : 1 -10
[本文引用: 1]
[11]
黄平 , 温诗铸 . 点、线接触真实粗糙表面的弹流润滑研究
. 力学学报 , 1993 , 25 (2 ): 302 -308
[本文引用: 1]
Huang Ping Wen Shizhu Study on elastohydrodynamic lubrication problems with real rough surfaces in line and point contacts
.Theoretical and Applied Mechanics , 1993 , 25 (2 ): 302 -308 (in Chinese)
[本文引用: 1]
[12]
Dowson D. Elasto-hydrodynamic Lubrication. Oxford : Pergamon Press , 1977 : 71
[本文引用: 1]
[13]
Chen H Ohyama T Yoahimura A Numerical analysis for the influence of water film on adhesion between rail and wheel
.Proc Inst Mech Engrs: Part J , 1998 , 212 : 359 -368
[本文引用: 2]
[14]
Patir N Cheng HS Average flow model for determining effects of 3-dimensional roughness on partial hydrodynamic lubrication
.J Lubri Technol Trans ASME , 1978 , 100 (1 ): 12 -17
[本文引用: 1]
[15]
Patir N Cheng HS Application of average flow model to lubrication between rough sliding surfaces
. J Lubri Technol Trans ASME , 1979 , 101 (2 ): 220 -230
[本文引用: 2]
[16]
Chen H Ban T Ishida M et al .Adhesion between rail/wheel under water lubricated contact
.Wear , 2002 , 253 : 75 -81
[本文引用: 1]
[17]
Chen H Ishida M Nakahara T Analysis of adhesion under wet conditions for three-dimensional contact considering surface roughness
.Wear , 2005 , 258 : 1209 -1216
[本文引用: 6]
[18]
Wu B Wen ZF Wang HY Numerical analysis on wheel-rail adhesion under mixed contamination of oil and water with surface roughness
.Wear , 2014 , 314 (1-2 ): 140 -147
[本文引用: 1]
[19]
Wu B Wen ZF Wang HY Analysis of wheel and rail adhesion under wet condition by using elastic-plastic microcontact model
.Lubri Sci , 2015 , 27 (4 ): 297 -312
[20]
Wu B Wen Z Wu T Analysis on thermal effect on high-speed wheel/rail adhesion under interfacial contamination using a three-dimensional model with surface roughness
.Wear , 2016 , 366 : 95 -104
[本文引用: 4]
[21]
Chen H Ban T Ishida M et al .Experimental investigation of influential factors on adhesion between wheel and rail under wet conditions
.Wear , 2008 , 265 (9-10 ): 1504 -1511
[本文引用: 2]
[22]
蔡宝春 , 蒋华臻 , 王文中 等 . 轮轨试样表面粗糙度取向对油润滑下摩擦系数的影响,
力学学报 ,2016 , 48 (4 ): 1114 -1125
[本文引用: 4]
Cai Baochun Jiang Huazhen Wang Wenzhong et al .Influence of surface roughness orientations on friction coefficient of wheel/rail specimen in oil lubrication
.Chinese J Theoretical and Applied Mechanics , 2016 , 48 (4 ): 1114 -1125 (in Chinese)
[本文引用: 4]
[23]
Zhu D Cheng HS Effect of surface roughness on the point contact EHL
.J Tribol Trans ASME , 1988 , 110 (1 ): 32 -37
[本文引用: 1]
[24]
Zhu D Hu YZ Effects of rough surface topography and orientation on the characteristics of EHD and mixed lubrication in both circular and elliptical contacts
.Tribol Trans , 2001 , 44 : 391 -398
[本文引用: 1]
[25]
Hu YZ Zhu D A full numerical solution to the mixed lubrication in point contacts
.J Tribol Trans ASME , 2000 , 122 (1 ): 1 -9
[本文引用: 1]
[26]
Bett KE Cappi JB Effect of pressure on the viscosity of water
.Nature , 1965 , 207 (4997 ): 620 -621
[本文引用: 1]
[27]
王文中 . 混合润滑的数值模拟和实验研究
[博士论文]. 北京: 清华大学 , 2003
Wang Wenzhong Numerical simulation and experimental studies on mixed Lubrication. [PhD Thesis]
. Beijing: Tsinghua University , 2003 (in Chinese )
[28]
Zhu D On some aspects in numerical solution of thin-film and mixed elastohydrodynamic lubrication
.Proc IMechE Part J J Eng Tribol , 2007 , 221 : 561 -579
[29]
Chen H Ishida M Namura A Estimation of wheel/rail adhesion coefficient under wet condition with measured boundary friction coefficient and real contact area
.Wear , 2011 , 271 (1-2 ): 32 -39
[30]
Dowson D Elastohydrodynamic and micro-elastohydrodynamic lubrication
.Wear , 1995 , 190 (2 ): 125 -138
[本文引用: 1]
[31]
刁晓明 . 服役动车组车轮磨耗及振动性能跟踪研究
[硕士论文]. 北京:北京交通大学 , 2014
[本文引用: 1]
Diao Xiaoming The track research on wheel wear and vibration performance of the service EMU in China. [Master Thesis]
. Beijing: Beijing Jiaotong University , 2014 (in Chinese )
[本文引用: 1]
[32]
Dowson D. Elastohydrodynamic lubrication. Pergmon Press , 1977
[33]
吴兵 . 高速轮轨黏着特性数值分析. [硕士论文]
. 成都: 西南交通大学 , 2009
[本文引用: 1]
Wu Bing Numerical analysis of wheel/rail adhesion characteristic for high-speed railway. [Master thesis]
. Chengdu: Xi’nan Jiaotong University , 2009 (in Chinese )
[本文引用: 1]
[34]
Gallardo-Hernandez EA Lewis R Twin disc assessment of wheel-rail adhesion
.Wear , 2008 , 265 (9-10 ): 1309 -1316
[本文引用: 1]
[35]
Baek KS Kyogoku K Nakahara T An experimental investigation of transient traction characteristics in rolling-sliding wheel-rail contacts under dry-wet conditions
. Wear 263 (2007 ): 169 -179
[36]
Wang WJ Wang H Wang HY Sub-scale simulation and measurement of railroad wheel/rail adhesion under dry and wet conditions
.Wear , 2013 , 302 (1-2 ): 1461 -1467
[37]
Wang WJ Lewis SR Lewis R et al .The role of slip ratio in rolling contact fatigue of rail materials under wet conditions
.Wear , 2017 , 376 : 1892 -1900
[38]
Lewis R Gallardo-Hernandez EA Hilton T et al .Effect of oil and water mixtures on adhesion in the wheel-rail contact
.P IMech Eng F J Rail & Rapid Transit 2009 , 223 (2 ): 275 -283
[本文引用: 1]
[39]
Jeffreys H The draining of a vertical plate
.Math Proc Cambri Philo Soci , 1930 , 26 : 204 -205
[本文引用: 1]
[40]
Moes H Optimum similarity analysis with applications to elastohydrodynamic lubrication
.Wear , 1992 , 59 (1 ): 57 -66
[41]
Akbarzadeh S Khonsari MM Effect of surface pattern on Stribeck curve
.Tribol Lett , 2010 , 37 (2 ): 477 -86
[42]
Akbarzadeh S Khonsari MM On the prediction of running in behavior in mixed-lubrication line contact
.J Tribol Trans ASME , 2010 , 132 (2 ): 032102
[本文引用: 1]
[43]
Zhu D Wang Q Effect of roughness orientation on the elastohydrodynamic lubrication film thickness
.J Tribol Trans ASME, 2013 , 135 (2 ): 031501
[本文引用: 1]
Tribological studies on adhesion phenomena between wheel and rail at high speed
1991
Traction and slip at higher rolling speeds: Some experiments under dry friction water lubrication
1983
Influence of surface contamination on adhesion force between wheel and rail at higher speeds-1st report-behavior of adhesion force under the surfaces contaminated with a small amount of liquid paraffin
1989
Influence of surface contamination on adhesion force between wheel and rail at higher speeds-2nd Report-effects of friction coefficients and tangential rigidity on adhesion force
1989
Influence of surface contamination on adhesion force between wheel and rail at higher speeds-3rd Report-behavior of adhesion force under the formation of lubricant film
1989
Wheel/rail adhesion and analysis by using full scale roller rig,
1
2002
... 轮轨黏着力是指车轮与钢轨在滚动接触时的切向力,是列车牵引和制动的主要动力,直接关系到列车运行的安全性、舒适性. 最 大黏着力与摩擦力有关,摩擦力的减小会导致黏着力的减小. 当轮轨间无液体(雨水、油污) 或固体(沙粒、树叶、锈) 等第三介质,并且处于直线段平稳运行时,黏着系数变化不大. 然而,日本新干线实测数据显示,对于湿润状态的轮轨接触,特别是列车运行速度超过200 km/h,黏着系数将显著下 降[1-3 ] . 这是因为:(1) 车轮与钢轨的接触区域可分为固体接触区和液体接触区,轮轨黏着力由这两个区域共同提供,与没有液体 时的情况相比,部分固体接触区域被液体隔开,而液体的剪切力远小于固体接触剪切力,因此,总的剪切力低于全部为固 体接触时的剪切力;(2) 水的黏度很低,对于高弹性模量材料(如:钢) 的高压接触,如果速度不是很大,例如:列车运行 在120 km/h 以下,水的润滑作用可以忽略,只有速度非常大,其流体动压效应才能形成一定厚度的水膜,从而体现出润滑作用. 早在20 世纪80 年代,Ohyama 等[4-7 ] 利用小尺度双盘对滚实验装置系统地研究了水、液态石蜡等液体介质存在 时,最高运动速度为200 km/h 的轮轨黏着系数与速度的演变关系. 在20 世纪90 年代,Zhang 等[8 ] 利用1:1 轮对滚动振动试验台研究了最高运动速度为280 km/h 时水润滑黏着系数与速度的 演变关系,得到的结论 是随着速度的增大,黏着系数不断减小. 对于速度更高的情况,以及轴重、温度等其他条件也变化的情况,如果都用实验研究,既不经济,有时也难以实施. 因此,利用数学模型,进行数值分析,研究轮轨黏着系数随速度、温度等因素的变化规律,可为实验研究和现场测试提供 重要的参考依据. ...
Friction in wheel-rail contact: A model comprising interfacial fluids, surface roughness and temperature
1
2011
... 关于水润滑轮轨接触研究的数学模型除了文献[9 ,10 ] 用界面流体模型以外,绝大多数研究者都采用基于雷诺方程的弹流 润滑(elasto-hydrodynamic lubrication, EHL) 模型[11 ] . 由于求解雷诺方程十分困难,通常采用Grubin 提出的近似解或数值解法[12 ] . Chen 等[13 ] 将轮轨接触简化为线接触,用Grubin 解首次计算了与轮轨表面粗糙度相关的、运动速度达300 km/h 的黏 着系数与速度的演变关系. 平均流量模型是Patir 提出的另一种求解雷诺方程的方法[14 ] ,该方法假设流经接触区的流量是恒定的,即:设定平均流量因子$\Phi_x$, $\Phi_y$,并利用参数$\gamma$表征表面形貌取向($\gamma <1$表示横纹, $\gamma =1$表示均匀形貌, $\gamma >1$表示纵纹,这种表征方法也称为随机模型). 该方法可求解与表面形貌取向相关的弹流润滑问题[15 ] . Chen 等[16 -17 ] 用该方法研究了表面粗糙度及其取向对水润滑轮轨黏着系数的影响规律. Wu 等[18 -20 ] 把平均流量模型推广到弹塑性接触并考虑接触热效应,给出了最高运动速度为350 km/h 时, 黏着系数与速度之间的关系. 文献[17 ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用. ...
Adhesion modeling in the wheel-rail contact under dry and lubricated conditions using measured 3D surfaces
1
2013
... 关于水润滑轮轨接触研究的数学模型除了文献[9 ,10 ] 用界面流体模型以外,绝大多数研究者都采用基于雷诺方程的弹流 润滑(elasto-hydrodynamic lubrication, EHL) 模型[11 ] . 由于求解雷诺方程十分困难,通常采用Grubin 提出的近似解或数值解法[12 ] . Chen 等[13 ] 将轮轨接触简化为线接触,用Grubin 解首次计算了与轮轨表面粗糙度相关的、运动速度达300 km/h 的黏 着系数与速度的演变关系. 平均流量模型是Patir 提出的另一种求解雷诺方程的方法[14 ] ,该方法假设流经接触区的流量是恒定的,即:设定平均流量因子$\Phi_x$, $\Phi_y$,并利用参数$\gamma$表征表面形貌取向($\gamma <1$表示横纹, $\gamma =1$表示均匀形貌, $\gamma >1$表示纵纹,这种表征方法也称为随机模型). 该方法可求解与表面形貌取向相关的弹流润滑问题[15 ] . Chen 等[16 -17 ] 用该方法研究了表面粗糙度及其取向对水润滑轮轨黏着系数的影响规律. Wu 等[18 -20 ] 把平均流量模型推广到弹塑性接触并考虑接触热效应,给出了最高运动速度为350 km/h 时, 黏着系数与速度之间的关系. 文献[17 ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用. ...
点、线接触真实粗糙表面的弹流润滑研究
1
1993
... 关于水润滑轮轨接触研究的数学模型除了文献[9 ,10 ] 用界面流体模型以外,绝大多数研究者都采用基于雷诺方程的弹流 润滑(elasto-hydrodynamic lubrication, EHL) 模型[11 ] . 由于求解雷诺方程十分困难,通常采用Grubin 提出的近似解或数值解法[12 ] . Chen 等[13 ] 将轮轨接触简化为线接触,用Grubin 解首次计算了与轮轨表面粗糙度相关的、运动速度达300 km/h 的黏 着系数与速度的演变关系. 平均流量模型是Patir 提出的另一种求解雷诺方程的方法[14 ] ,该方法假设流经接触区的流量是恒定的,即:设定平均流量因子$\Phi_x$, $\Phi_y$,并利用参数$\gamma$表征表面形貌取向($\gamma <1$表示横纹, $\gamma =1$表示均匀形貌, $\gamma >1$表示纵纹,这种表征方法也称为随机模型). 该方法可求解与表面形貌取向相关的弹流润滑问题[15 ] . Chen 等[16 -17 ] 用该方法研究了表面粗糙度及其取向对水润滑轮轨黏着系数的影响规律. Wu 等[18 -20 ] 把平均流量模型推广到弹塑性接触并考虑接触热效应,给出了最高运动速度为350 km/h 时, 黏着系数与速度之间的关系. 文献[17 ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用. ...
点、线接触真实粗糙表面的弹流润滑研究
1
1993
... 关于水润滑轮轨接触研究的数学模型除了文献[9 ,10 ] 用界面流体模型以外,绝大多数研究者都采用基于雷诺方程的弹流 润滑(elasto-hydrodynamic lubrication, EHL) 模型[11 ] . 由于求解雷诺方程十分困难,通常采用Grubin 提出的近似解或数值解法[12 ] . Chen 等[13 ] 将轮轨接触简化为线接触,用Grubin 解首次计算了与轮轨表面粗糙度相关的、运动速度达300 km/h 的黏 着系数与速度的演变关系. 平均流量模型是Patir 提出的另一种求解雷诺方程的方法[14 ] ,该方法假设流经接触区的流量是恒定的,即:设定平均流量因子$\Phi_x$, $\Phi_y$,并利用参数$\gamma$表征表面形貌取向($\gamma <1$表示横纹, $\gamma =1$表示均匀形貌, $\gamma >1$表示纵纹,这种表征方法也称为随机模型). 该方法可求解与表面形貌取向相关的弹流润滑问题[15 ] . Chen 等[16 -17 ] 用该方法研究了表面粗糙度及其取向对水润滑轮轨黏着系数的影响规律. Wu 等[18 -20 ] 把平均流量模型推广到弹塑性接触并考虑接触热效应,给出了最高运动速度为350 km/h 时, 黏着系数与速度之间的关系. 文献[17 ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用. ...
1
1977
... 关于水润滑轮轨接触研究的数学模型除了文献[9 ,10 ] 用界面流体模型以外,绝大多数研究者都采用基于雷诺方程的弹流 润滑(elasto-hydrodynamic lubrication, EHL) 模型[11 ] . 由于求解雷诺方程十分困难,通常采用Grubin 提出的近似解或数值解法[12 ] . Chen 等[13 ] 将轮轨接触简化为线接触,用Grubin 解首次计算了与轮轨表面粗糙度相关的、运动速度达300 km/h 的黏 着系数与速度的演变关系. 平均流量模型是Patir 提出的另一种求解雷诺方程的方法[14 ] ,该方法假设流经接触区的流量是恒定的,即:设定平均流量因子$\Phi_x$, $\Phi_y$,并利用参数$\gamma$表征表面形貌取向($\gamma <1$表示横纹, $\gamma =1$表示均匀形貌, $\gamma >1$表示纵纹,这种表征方法也称为随机模型). 该方法可求解与表面形貌取向相关的弹流润滑问题[15 ] . Chen 等[16 -17 ] 用该方法研究了表面粗糙度及其取向对水润滑轮轨黏着系数的影响规律. Wu 等[18 -20 ] 把平均流量模型推广到弹塑性接触并考虑接触热效应,给出了最高运动速度为350 km/h 时, 黏着系数与速度之间的关系. 文献[17 ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用. ...
Numerical analysis for the influence of water film on adhesion between rail and wheel
2
1998
... 关于水润滑轮轨接触研究的数学模型除了文献[9 ,10 ] 用界面流体模型以外,绝大多数研究者都采用基于雷诺方程的弹流 润滑(elasto-hydrodynamic lubrication, EHL) 模型[11 ] . 由于求解雷诺方程十分困难,通常采用Grubin 提出的近似解或数值解法[12 ] . Chen 等[13 ] 将轮轨接触简化为线接触,用Grubin 解首次计算了与轮轨表面粗糙度相关的、运动速度达300 km/h 的黏 着系数与速度的演变关系. 平均流量模型是Patir 提出的另一种求解雷诺方程的方法[14 ] ,该方法假设流经接触区的流量是恒定的,即:设定平均流量因子$\Phi_x$, $\Phi_y$,并利用参数$\gamma$表征表面形貌取向($\gamma <1$表示横纹, $\gamma =1$表示均匀形貌, $\gamma >1$表示纵纹,这种表征方法也称为随机模型). 该方法可求解与表面形貌取向相关的弹流润滑问题[15 ] . Chen 等[16 -17 ] 用该方法研究了表面粗糙度及其取向对水润滑轮轨黏着系数的影响规律. Wu 等[18 -20 ] 把平均流量模型推广到弹塑性接触并考虑接触热效应,给出了最高运动速度为350 km/h 时, 黏着系数与速度之间的关系. 文献[17 ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用. ...
... 式中,$\eta_{0}$ 为水的常温(20${^\circ}$C) 黏度, $\eta_{1}$, $\eta _{2}$, $\eta _{3}$, $\eta_{4}$ 采用陈桦等的拟合结果[13 ] . 水的密度按下式计算 ...
Average flow model for determining effects of 3-dimensional roughness on partial hydrodynamic lubrication
1
1978
... 关于水润滑轮轨接触研究的数学模型除了文献[9 ,10 ] 用界面流体模型以外,绝大多数研究者都采用基于雷诺方程的弹流 润滑(elasto-hydrodynamic lubrication, EHL) 模型[11 ] . 由于求解雷诺方程十分困难,通常采用Grubin 提出的近似解或数值解法[12 ] . Chen 等[13 ] 将轮轨接触简化为线接触,用Grubin 解首次计算了与轮轨表面粗糙度相关的、运动速度达300 km/h 的黏 着系数与速度的演变关系. 平均流量模型是Patir 提出的另一种求解雷诺方程的方法[14 ] ,该方法假设流经接触区的流量是恒定的,即:设定平均流量因子$\Phi_x$, $\Phi_y$,并利用参数$\gamma$表征表面形貌取向($\gamma <1$表示横纹, $\gamma =1$表示均匀形貌, $\gamma >1$表示纵纹,这种表征方法也称为随机模型). 该方法可求解与表面形貌取向相关的弹流润滑问题[15 ] . Chen 等[16 -17 ] 用该方法研究了表面粗糙度及其取向对水润滑轮轨黏着系数的影响规律. Wu 等[18 -20 ] 把平均流量模型推广到弹塑性接触并考虑接触热效应,给出了最高运动速度为350 km/h 时, 黏着系数与速度之间的关系. 文献[17 ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用. ...
Application of average flow model to lubrication between rough sliding surfaces
2
1979
... 关于水润滑轮轨接触研究的数学模型除了文献[9 ,10 ] 用界面流体模型以外,绝大多数研究者都采用基于雷诺方程的弹流 润滑(elasto-hydrodynamic lubrication, EHL) 模型[11 ] . 由于求解雷诺方程十分困难,通常采用Grubin 提出的近似解或数值解法[12 ] . Chen 等[13 ] 将轮轨接触简化为线接触,用Grubin 解首次计算了与轮轨表面粗糙度相关的、运动速度达300 km/h 的黏 着系数与速度的演变关系. 平均流量模型是Patir 提出的另一种求解雷诺方程的方法[14 ] ,该方法假设流经接触区的流量是恒定的,即:设定平均流量因子$\Phi_x$, $\Phi_y$,并利用参数$\gamma$表征表面形貌取向($\gamma <1$表示横纹, $\gamma =1$表示均匀形貌, $\gamma >1$表示纵纹,这种表征方法也称为随机模型). 该方法可求解与表面形貌取向相关的弹流润滑问题[15 ] . Chen 等[16 -17 ] 用该方法研究了表面粗糙度及其取向对水润滑轮轨黏着系数的影响规律. Wu 等[18 -20 ] 把平均流量模型推广到弹塑性接触并考虑接触热效应,给出了最高运动速度为350 km/h 时, 黏着系数与速度之间的关系. 文献[17 ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用. ...
... 从物理上说,无论接触区形状如何,对于具有特定取向的表面形貌,横纹和菱形对来流的阻碍作用比纵纹大,导致液体流向接触 区外,即侧流效应较为显著. 相反,纵纹有利于液体通过接触区,侧流效应相对较弱,纵纹比横纹和菱形可形成更厚的水膜,因此,纵纹黏着系数较小. 只有在宽度大于长度的线接触中或椭圆率$k \gg 1$的点接触中,并且液体黏度较大时,才有可能出现侧流效应可忽略的情况,即Patir 所谓的宽轴承情况[15 ] ,使横纹对 来流的阻碍作用导致膜厚增大,黏着系数减小. ...
Adhesion between rail/wheel under water lubricated contact
1
2002
... 关于水润滑轮轨接触研究的数学模型除了文献[9 ,10 ] 用界面流体模型以外,绝大多数研究者都采用基于雷诺方程的弹流 润滑(elasto-hydrodynamic lubrication, EHL) 模型[11 ] . 由于求解雷诺方程十分困难,通常采用Grubin 提出的近似解或数值解法[12 ] . Chen 等[13 ] 将轮轨接触简化为线接触,用Grubin 解首次计算了与轮轨表面粗糙度相关的、运动速度达300 km/h 的黏 着系数与速度的演变关系. 平均流量模型是Patir 提出的另一种求解雷诺方程的方法[14 ] ,该方法假设流经接触区的流量是恒定的,即:设定平均流量因子$\Phi_x$, $\Phi_y$,并利用参数$\gamma$表征表面形貌取向($\gamma <1$表示横纹, $\gamma =1$表示均匀形貌, $\gamma >1$表示纵纹,这种表征方法也称为随机模型). 该方法可求解与表面形貌取向相关的弹流润滑问题[15 ] . Chen 等[16 -17 ] 用该方法研究了表面粗糙度及其取向对水润滑轮轨黏着系数的影响规律. Wu 等[18 -20 ] 把平均流量模型推广到弹塑性接触并考虑接触热效应,给出了最高运动速度为350 km/h 时, 黏着系数与速度之间的关系. 文献[17 ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用. ...
Analysis of adhesion under wet conditions for three-dimensional contact considering surface roughness
6
2005
... 关于水润滑轮轨接触研究的数学模型除了文献[9 ,10 ] 用界面流体模型以外,绝大多数研究者都采用基于雷诺方程的弹流 润滑(elasto-hydrodynamic lubrication, EHL) 模型[11 ] . 由于求解雷诺方程十分困难,通常采用Grubin 提出的近似解或数值解法[12 ] . Chen 等[13 ] 将轮轨接触简化为线接触,用Grubin 解首次计算了与轮轨表面粗糙度相关的、运动速度达300 km/h 的黏 着系数与速度的演变关系. 平均流量模型是Patir 提出的另一种求解雷诺方程的方法[14 ] ,该方法假设流经接触区的流量是恒定的,即:设定平均流量因子$\Phi_x$, $\Phi_y$,并利用参数$\gamma$表征表面形貌取向($\gamma <1$表示横纹, $\gamma =1$表示均匀形貌, $\gamma >1$表示纵纹,这种表征方法也称为随机模型). 该方法可求解与表面形貌取向相关的弹流润滑问题[15 ] . Chen 等[16 -17 ] 用该方法研究了表面粗糙度及其取向对水润滑轮轨黏着系数的影响规律. Wu 等[18 -20 ] 把平均流量模型推广到弹塑性接触并考虑接触热效应,给出了最高运动速度为350 km/h 时, 黏着系数与速度之间的关系. 文献[17 ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用. ...
... 把平均流量模型推广到弹塑性接触并考虑接触热效应,给出了最高运动速度为350 km/h 时, 黏着系数与速度之间的关系. 文献[17 ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用. ...
... The parameters used in the numerical simulation
Parameters Value Effective elastic modulusE' / GPa 242 Poisson's ratio $\nu $ 0.3 $R_{1x}$/m 0.45[17 ] $R_{2y}$/m 0.30[17 ] Temperature/${^\circ}$C 20 Normal load/N 8.50 #x00D7;10 4 Velocity/(km$\cdot$h$^{-1}$) 100, 200, 300, 400, 500 Creep rate % 0.0001,0.30, 0.50, 1.0, 1.5, 2.0 Viscosity at room 0.001 01 Density of water at room 1.00
3 结果与讨论 3.1 压力与膜厚 通过求解雷诺方程,得到具有规则形貌的车轮与钢轨接触时,接触区的压力与膜厚的分布. 图4 至图7 表示运动速度为300 km/h,蠕滑率为1.0%,具有随机形貌和横纹、纵纹、菱形形貌的车轮与钢轨接触时的压 力、膜厚分布. 其中,图4 ~图7 中的(a) 图和(b) 图分别为接触区中心线上的二维压力与膜厚分布(其中$h_a$为轮轨间的名义接触区内的平均膜厚或者平均间隙),图4 ~图7 中的(c) 图为接触区的膜厚云图. ...
... [
17 ]
Temperature/${^\circ}$C 20 Normal load/N 8.50 #x00D7;10 4 Velocity/(km$\cdot$h$^{-1}$) 100, 200, 300, 400, 500 Creep rate % 0.0001,0.30, 0.50, 1.0, 1.5, 2.0 Viscosity at room 0.001 01 Density of water at room 1.00 3 结果与讨论 3.1 压力与膜厚 通过求解雷诺方程,得到具有规则形貌的车轮与钢轨接触时,接触区的压力与膜厚的分布. 图4 至图7 表示运动速度为300 km/h,蠕滑率为1.0%,具有随机形貌和横纹、纵纹、菱形形貌的车轮与钢轨接触时的压 力、膜厚分布. 其中,图4 ~图7 中的(a) 图和(b) 图分别为接触区中心线上的二维压力与膜厚分布(其中$h_a$为轮轨间的名义接触区内的平均膜厚或者平均间隙),图4 ~图7 中的(c) 图为接触区的膜厚云图. ...
... 当运动速度较低时,譬如,速度为100 km/h,3 种规则形貌的黏着系数相差不大. 但是,当速度超过200 km/h,3 种规 则形貌的黏着系数明显大于随机形貌的黏着系数. 这说明,激光规则形貌可有效提高水润滑轮轨黏着系数. 特别值得注意的是,计算结果表明菱形的黏着系数大于横纹的黏着系数,而纵纹的黏着系数又小于横纹的. 这与平均流量模型的计算结果正好相反[17 -20 ] ,而与高速轮轨水润滑黏着系数的实验结果相符[21 ] . ...
... 本文作者用统一雷诺方程模型研究了表面形貌取向对黏着系数的影响规律,对于油润滑、线接触,结论是[22 ] :$\mu_{\hbox{菱形}}> \mu_{\hbox{纵纹}}> \mu _{\hbox{横纹}}$,对于水润滑、$k<1$ 的点接触,结论是: $\mu_{\hbox{菱形}}> \mu_{\hbox{横纹}}> \mu_{\hbox{纵纹}}$. 这充分说明,关于表面形貌取向对黏着系数的影响规律不是一成不变的. 表面形貌取向、黏度、接触区形状等因素决定了接触区的流动状态,进而改变固体接触压力与总压力之比. 方程(9) 表明,在混合润滑状态下,影响黏着系数的主要原因是固体接触压力与总压力之比[17 ] . 表2 是速度为300 km/h,蠕滑率为1.0% 时,接触压力与总压力的比值. 可以看出比值的大小关系为,菱形大于横纹,横纹大于纵纹,而纵纹又大于随机形貌. 因此,黏着系数大小的顺序为:菱形的最大,横纹其次,纵纹次之,随机形貌的最小. ...
Numerical analysis on wheel-rail adhesion under mixed contamination of oil and water with surface roughness
1
2014
... 关于水润滑轮轨接触研究的数学模型除了文献[9 ,10 ] 用界面流体模型以外,绝大多数研究者都采用基于雷诺方程的弹流 润滑(elasto-hydrodynamic lubrication, EHL) 模型[11 ] . 由于求解雷诺方程十分困难,通常采用Grubin 提出的近似解或数值解法[12 ] . Chen 等[13 ] 将轮轨接触简化为线接触,用Grubin 解首次计算了与轮轨表面粗糙度相关的、运动速度达300 km/h 的黏 着系数与速度的演变关系. 平均流量模型是Patir 提出的另一种求解雷诺方程的方法[14 ] ,该方法假设流经接触区的流量是恒定的,即:设定平均流量因子$\Phi_x$, $\Phi_y$,并利用参数$\gamma$表征表面形貌取向($\gamma <1$表示横纹, $\gamma =1$表示均匀形貌, $\gamma >1$表示纵纹,这种表征方法也称为随机模型). 该方法可求解与表面形貌取向相关的弹流润滑问题[15 ] . Chen 等[16 -17 ] 用该方法研究了表面粗糙度及其取向对水润滑轮轨黏着系数的影响规律. Wu 等[18 -20 ] 把平均流量模型推广到弹塑性接触并考虑接触热效应,给出了最高运动速度为350 km/h 时, 黏着系数与速度之间的关系. 文献[17 ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用. ...
Analysis of wheel and rail adhesion under wet condition by using elastic-plastic microcontact model
2015
Analysis on thermal effect on high-speed wheel/rail adhesion under interfacial contamination using a three-dimensional model with surface roughness
4
2016
... 关于水润滑轮轨接触研究的数学模型除了文献[9 ,10 ] 用界面流体模型以外,绝大多数研究者都采用基于雷诺方程的弹流 润滑(elasto-hydrodynamic lubrication, EHL) 模型[11 ] . 由于求解雷诺方程十分困难,通常采用Grubin 提出的近似解或数值解法[12 ] . Chen 等[13 ] 将轮轨接触简化为线接触,用Grubin 解首次计算了与轮轨表面粗糙度相关的、运动速度达300 km/h 的黏 着系数与速度的演变关系. 平均流量模型是Patir 提出的另一种求解雷诺方程的方法[14 ] ,该方法假设流经接触区的流量是恒定的,即:设定平均流量因子$\Phi_x$, $\Phi_y$,并利用参数$\gamma$表征表面形貌取向($\gamma <1$表示横纹, $\gamma =1$表示均匀形貌, $\gamma >1$表示纵纹,这种表征方法也称为随机模型). 该方法可求解与表面形貌取向相关的弹流润滑问题[15 ] . Chen 等[16 -17 ] 用该方法研究了表面粗糙度及其取向对水润滑轮轨黏着系数的影响规律. Wu 等[18 -20 ] 把平均流量模型推广到弹塑性接触并考虑接触热效应,给出了最高运动速度为350 km/h 时, 黏着系数与速度之间的关系. 文献[17 ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用. ...
... ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用. ...
... 计算表明,(1) 在水润滑状态下,随机形貌以及纵纹、横纹、菱形对应的轮轨黏着系数都随速度的增大而降低(图8 和图9 只显示 蠕滑率分别为0.3% 和2.0% 的两情况). 这与油润滑或其他液体润滑的结果是一致的,即:流体动压随速度的增大而增大,膜厚增大,因而,黏着系数减小. (2) 蠕滑率$s$的变化对黏着系数的影响不大,如图10 (图中仅显示了300 km/h 时的情况). 这是因为本文的计算没有考虑接触摩擦热导致的温度的变化,这与文献[33 ] 的结果是一致的. 如果考虑接触摩擦热使轮轨接触区温度升高,则对应的黏着系数都减小[20 ] . 无论是干接触态还是润滑态,各种实验结果都显示,当蠕滑率增大到一定程度时,黏着系数有一个峰值,过了峰值之后, 黏着系数将随蠕滑率的增大而减小[34 -38 ] . 因为在实验中,接触摩擦热是必定存在的. ...
... 当运动速度较低时,譬如,速度为100 km/h,3 种规则形貌的黏着系数相差不大. 但是,当速度超过200 km/h,3 种规 则形貌的黏着系数明显大于随机形貌的黏着系数. 这说明,激光规则形貌可有效提高水润滑轮轨黏着系数. 特别值得注意的是,计算结果表明菱形的黏着系数大于横纹的黏着系数,而纵纹的黏着系数又小于横纹的. 这与平均流量模型的计算结果正好相反[17 -20 ] ,而与高速轮轨水润滑黏着系数的实验结果相符[21 ] . ...
Experimental investigation of influential factors on adhesion between wheel and rail under wet conditions
2
2008
... 关于水润滑轮轨接触研究的数学模型除了文献[9 ,10 ] 用界面流体模型以外,绝大多数研究者都采用基于雷诺方程的弹流 润滑(elasto-hydrodynamic lubrication, EHL) 模型[11 ] . 由于求解雷诺方程十分困难,通常采用Grubin 提出的近似解或数值解法[12 ] . Chen 等[13 ] 将轮轨接触简化为线接触,用Grubin 解首次计算了与轮轨表面粗糙度相关的、运动速度达300 km/h 的黏 着系数与速度的演变关系. 平均流量模型是Patir 提出的另一种求解雷诺方程的方法[14 ] ,该方法假设流经接触区的流量是恒定的,即:设定平均流量因子$\Phi_x$, $\Phi_y$,并利用参数$\gamma$表征表面形貌取向($\gamma <1$表示横纹, $\gamma =1$表示均匀形貌, $\gamma >1$表示纵纹,这种表征方法也称为随机模型). 该方法可求解与表面形貌取向相关的弹流润滑问题[15 ] . Chen 等[16 -17 ] 用该方法研究了表面粗糙度及其取向对水润滑轮轨黏着系数的影响规律. Wu 等[18 -20 ] 把平均流量模型推广到弹塑性接触并考虑接触热效应,给出了最高运动速度为350 km/h 时, 黏着系数与速度之间的关系. 文献[17 ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用. ...
... 当运动速度较低时,譬如,速度为100 km/h,3 种规则形貌的黏着系数相差不大. 但是,当速度超过200 km/h,3 种规 则形貌的黏着系数明显大于随机形貌的黏着系数. 这说明,激光规则形貌可有效提高水润滑轮轨黏着系数. 特别值得注意的是,计算结果表明菱形的黏着系数大于横纹的黏着系数,而纵纹的黏着系数又小于横纹的. 这与平均流量模型的计算结果正好相反[17 -20 ] ,而与高速轮轨水润滑黏着系数的实验结果相符[21 ] . ...
轮轨试样表面粗糙度取向对油润滑下摩擦系数的影响,
4
2016
... 关于水润滑轮轨接触研究的数学模型除了文献[9 ,10 ] 用界面流体模型以外,绝大多数研究者都采用基于雷诺方程的弹流 润滑(elasto-hydrodynamic lubrication, EHL) 模型[11 ] . 由于求解雷诺方程十分困难,通常采用Grubin 提出的近似解或数值解法[12 ] . Chen 等[13 ] 将轮轨接触简化为线接触,用Grubin 解首次计算了与轮轨表面粗糙度相关的、运动速度达300 km/h 的黏 着系数与速度的演变关系. 平均流量模型是Patir 提出的另一种求解雷诺方程的方法[14 ] ,该方法假设流经接触区的流量是恒定的,即:设定平均流量因子$\Phi_x$, $\Phi_y$,并利用参数$\gamma$表征表面形貌取向($\gamma <1$表示横纹, $\gamma =1$表示均匀形貌, $\gamma >1$表示纵纹,这种表征方法也称为随机模型). 该方法可求解与表面形貌取向相关的弹流润滑问题[15 ] . Chen 等[16 -17 ] 用该方法研究了表面粗糙度及其取向对水润滑轮轨黏着系数的影响规律. Wu 等[18 -20 ] 把平均流量模型推广到弹塑性接触并考虑接触热效应,给出了最高运动速度为350 km/h 时, 黏着系数与速度之间的关系. 文献[17 ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用. ...
... 本文采用文献[25 ] 提出的统一雷诺方程模型计算水润滑轮轨接触问题,该模型的核心思想是:当液膜或间隙为零 时,利用退化的雷诺方程可以求解干接触问题. 因此,对固体接触区和液体接触区都用雷诺方程求解,从而避免了确定固体区与液体区边界条件所带来的困难. 在形貌方面,以实测的表面形貌为基础,以拟合的形貌函数为输入文件. 在文献[22 ] 的基础上,将统一雷诺方程模型用于计算车轮表面具有宏观规则形貌的水润滑高速轮轨接触,研究表面 形貌取向、黏着系数及运动速度的之间关系. ...
... 文献[22 ] 在小尺度试样表面制备了激光毛化形貌,单个激光毛化形貌的直径约为150 m,深度约为3 m (图1 ),这些单个激光形貌以400 m 和 200 m 的间距规则分布,形成纵纹、横纹、菱形三种宏观形貌. 由于高速列车车轮踏面的平均磨耗约为230 ~ 500 m 每10 万公里[31 ] ,从实际应用的角度考虑,本文将单个激光形貌及其分布按比例放大,构建车轮表面激光宏观规则 形貌,使单个激光形貌的直径约为1.0 mm. 图2 (a) 为采用二维分段函数拟合的半个激光形貌的纵剖面,函数表达式如下 ...
... 本文作者用统一雷诺方程模型研究了表面形貌取向对黏着系数的影响规律,对于油润滑、线接触,结论是[22 ] :$\mu_{\hbox{菱形}}> \mu_{\hbox{纵纹}}> \mu _{\hbox{横纹}}$,对于水润滑、$k<1$ 的点接触,结论是: $\mu_{\hbox{菱形}}> \mu_{\hbox{横纹}}> \mu_{\hbox{纵纹}}$. 这充分说明,关于表面形貌取向对黏着系数的影响规律不是一成不变的. 表面形貌取向、黏度、接触区形状等因素决定了接触区的流动状态,进而改变固体接触压力与总压力之比. 方程(9) 表明,在混合润滑状态下,影响黏着系数的主要原因是固体接触压力与总压力之比[17 ] . 表2 是速度为300 km/h,蠕滑率为1.0% 时,接触压力与总压力的比值. 可以看出比值的大小关系为,菱形大于横纹,横纹大于纵纹,而纵纹又大于随机形貌. 因此,黏着系数大小的顺序为:菱形的最大,横纹其次,纵纹次之,随机形貌的最小. ...
轮轨试样表面粗糙度取向对油润滑下摩擦系数的影响,
4
2016
... 关于水润滑轮轨接触研究的数学模型除了文献[9 ,10 ] 用界面流体模型以外,绝大多数研究者都采用基于雷诺方程的弹流 润滑(elasto-hydrodynamic lubrication, EHL) 模型[11 ] . 由于求解雷诺方程十分困难,通常采用Grubin 提出的近似解或数值解法[12 ] . Chen 等[13 ] 将轮轨接触简化为线接触,用Grubin 解首次计算了与轮轨表面粗糙度相关的、运动速度达300 km/h 的黏 着系数与速度的演变关系. 平均流量模型是Patir 提出的另一种求解雷诺方程的方法[14 ] ,该方法假设流经接触区的流量是恒定的,即:设定平均流量因子$\Phi_x$, $\Phi_y$,并利用参数$\gamma$表征表面形貌取向($\gamma <1$表示横纹, $\gamma =1$表示均匀形貌, $\gamma >1$表示纵纹,这种表征方法也称为随机模型). 该方法可求解与表面形貌取向相关的弹流润滑问题[15 ] . Chen 等[16 -17 ] 用该方法研究了表面粗糙度及其取向对水润滑轮轨黏着系数的影响规律. Wu 等[18 -20 ] 把平均流量模型推广到弹塑性接触并考虑接触热效应,给出了最高运动速度为350 km/h 时, 黏着系数与速度之间的关系. 文献[17 ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用. ...
... 本文采用文献[25 ] 提出的统一雷诺方程模型计算水润滑轮轨接触问题,该模型的核心思想是:当液膜或间隙为零 时,利用退化的雷诺方程可以求解干接触问题. 因此,对固体接触区和液体接触区都用雷诺方程求解,从而避免了确定固体区与液体区边界条件所带来的困难. 在形貌方面,以实测的表面形貌为基础,以拟合的形貌函数为输入文件. 在文献[22 ] 的基础上,将统一雷诺方程模型用于计算车轮表面具有宏观规则形貌的水润滑高速轮轨接触,研究表面 形貌取向、黏着系数及运动速度的之间关系. ...
... 文献[22 ] 在小尺度试样表面制备了激光毛化形貌,单个激光毛化形貌的直径约为150 m,深度约为3 m (图1 ),这些单个激光形貌以400 m 和 200 m 的间距规则分布,形成纵纹、横纹、菱形三种宏观形貌. 由于高速列车车轮踏面的平均磨耗约为230 ~ 500 m 每10 万公里[31 ] ,从实际应用的角度考虑,本文将单个激光形貌及其分布按比例放大,构建车轮表面激光宏观规则 形貌,使单个激光形貌的直径约为1.0 mm. 图2 (a) 为采用二维分段函数拟合的半个激光形貌的纵剖面,函数表达式如下 ...
... 本文作者用统一雷诺方程模型研究了表面形貌取向对黏着系数的影响规律,对于油润滑、线接触,结论是[22 ] :$\mu_{\hbox{菱形}}> \mu_{\hbox{纵纹}}> \mu _{\hbox{横纹}}$,对于水润滑、$k<1$ 的点接触,结论是: $\mu_{\hbox{菱形}}> \mu_{\hbox{横纹}}> \mu_{\hbox{纵纹}}$. 这充分说明,关于表面形貌取向对黏着系数的影响规律不是一成不变的. 表面形貌取向、黏度、接触区形状等因素决定了接触区的流动状态,进而改变固体接触压力与总压力之比. 方程(9) 表明,在混合润滑状态下,影响黏着系数的主要原因是固体接触压力与总压力之比[17 ] . 表2 是速度为300 km/h,蠕滑率为1.0% 时,接触压力与总压力的比值. 可以看出比值的大小关系为,菱形大于横纹,横纹大于纵纹,而纵纹又大于随机形貌. 因此,黏着系数大小的顺序为:菱形的最大,横纹其次,纵纹次之,随机形貌的最小. ...
Effect of surface roughness on the point contact EHL
1
1988
... 关于水润滑轮轨接触研究的数学模型除了文献[9 ,10 ] 用界面流体模型以外,绝大多数研究者都采用基于雷诺方程的弹流 润滑(elasto-hydrodynamic lubrication, EHL) 模型[11 ] . 由于求解雷诺方程十分困难,通常采用Grubin 提出的近似解或数值解法[12 ] . Chen 等[13 ] 将轮轨接触简化为线接触,用Grubin 解首次计算了与轮轨表面粗糙度相关的、运动速度达300 km/h 的黏 着系数与速度的演变关系. 平均流量模型是Patir 提出的另一种求解雷诺方程的方法[14 ] ,该方法假设流经接触区的流量是恒定的,即:设定平均流量因子$\Phi_x$, $\Phi_y$,并利用参数$\gamma$表征表面形貌取向($\gamma <1$表示横纹, $\gamma =1$表示均匀形貌, $\gamma >1$表示纵纹,这种表征方法也称为随机模型). 该方法可求解与表面形貌取向相关的弹流润滑问题[15 ] . Chen 等[16 -17 ] 用该方法研究了表面粗糙度及其取向对水润滑轮轨黏着系数的影响规律. Wu 等[18 -20 ] 把平均流量模型推广到弹塑性接触并考虑接触热效应,给出了最高运动速度为350 km/h 时, 黏着系数与速度之间的关系. 文献[17 ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用. ...
Effects of rough surface topography and orientation on the characteristics of EHD and mixed lubrication in both circular and elliptical contacts
1
2001
... 关于水润滑轮轨接触研究的数学模型除了文献[9 ,10 ] 用界面流体模型以外,绝大多数研究者都采用基于雷诺方程的弹流 润滑(elasto-hydrodynamic lubrication, EHL) 模型[11 ] . 由于求解雷诺方程十分困难,通常采用Grubin 提出的近似解或数值解法[12 ] . Chen 等[13 ] 将轮轨接触简化为线接触,用Grubin 解首次计算了与轮轨表面粗糙度相关的、运动速度达300 km/h 的黏 着系数与速度的演变关系. 平均流量模型是Patir 提出的另一种求解雷诺方程的方法[14 ] ,该方法假设流经接触区的流量是恒定的,即:设定平均流量因子$\Phi_x$, $\Phi_y$,并利用参数$\gamma$表征表面形貌取向($\gamma <1$表示横纹, $\gamma =1$表示均匀形貌, $\gamma >1$表示纵纹,这种表征方法也称为随机模型). 该方法可求解与表面形貌取向相关的弹流润滑问题[15 ] . Chen 等[16 -17 ] 用该方法研究了表面粗糙度及其取向对水润滑轮轨黏着系数的影响规律. Wu 等[18 -20 ] 把平均流量模型推广到弹塑性接触并考虑接触热效应,给出了最高运动速度为350 km/h 时, 黏着系数与速度之间的关系. 文献[17 ,20 ] 模拟计算结果都认为:横纹形貌的黏着系数小于纵纹形貌的黏着系数. 这与高速轮轨水润滑黏着系数的实验结果相矛盾[21 ] . 本文作者曾经指出[22 ] ,平均流量模型的主要假设是接触区流量恒定,这相当于在物理上忽略了侧流. 因此,当侧流不能忽略时,采用平均流量模型进行计算将带来较大的误差. Zhu 等[23 -24 ] 也指出,平均流量模型在数量上夸大了横纹对来流的阻碍作用. ...
A full numerical solution to the mixed lubrication in point contacts
1
2000
... 本文采用文献[25 ] 提出的统一雷诺方程模型计算水润滑轮轨接触问题,该模型的核心思想是:当液膜或间隙为零 时,利用退化的雷诺方程可以求解干接触问题. 因此,对固体接触区和液体接触区都用雷诺方程求解,从而避免了确定固体区与液体区边界条件所带来的困难. 在形貌方面,以实测的表面形貌为基础,以拟合的形貌函数为输入文件. 在文献[22 ] 的基础上,将统一雷诺方程模型用于计算车轮表面具有宏观规则形貌的水润滑高速轮轨接触,研究表面 形貌取向、黏着系数及运动速度的之间关系. ...
Effect of pressure on the viscosity of water
1
1965
... 水看作可压缩牛顿流体,方程(1) 中$\eta $代表水的黏压关系[26 ] ...
On some aspects in numerical solution of thin-film and mixed elastohydrodynamic lubrication
2007
Estimation of wheel/rail adhesion coefficient under wet condition with measured boundary friction coefficient and real contact area
2011
Elastohydrodynamic and micro-elastohydrodynamic lubrication
1
1995
... 其中, $\mu_{\rm s}$ 是固体接触区的摩擦系数,它的大小由边界条件决定,一般由实验确定. 对于水的混合润滑,通常取0.14$\sim $0.45 之间的数值[16, 29 ] ,本文取0.2. $\mu _{\rm l}P_{\rml}$ 为液体接触区的剪切力,对于水润滑条件,剪切力满足如下牛顿流体形式[30 ] ...
服役动车组车轮磨耗及振动性能跟踪研究
1
2014
... 文献[22 ] 在小尺度试样表面制备了激光毛化形貌,单个激光毛化形貌的直径约为150 m,深度约为3 m (图1 ),这些单个激光形貌以400 m 和 200 m 的间距规则分布,形成纵纹、横纹、菱形三种宏观形貌. 由于高速列车车轮踏面的平均磨耗约为230 ~ 500 m 每10 万公里[31 ] ,从实际应用的角度考虑,本文将单个激光形貌及其分布按比例放大,构建车轮表面激光宏观规则 形貌,使单个激光形貌的直径约为1.0 mm. 图2 (a) 为采用二维分段函数拟合的半个激光形貌的纵剖面,函数表达式如下 ...
服役动车组车轮磨耗及振动性能跟踪研究
1
2014
... 文献[22 ] 在小尺度试样表面制备了激光毛化形貌,单个激光毛化形貌的直径约为150 m,深度约为3 m (图1 ),这些单个激光形貌以400 m 和 200 m 的间距规则分布,形成纵纹、横纹、菱形三种宏观形貌. 由于高速列车车轮踏面的平均磨耗约为230 ~ 500 m 每10 万公里[31 ] ,从实际应用的角度考虑,本文将单个激光形貌及其分布按比例放大,构建车轮表面激光宏观规则 形貌,使单个激光形貌的直径约为1.0 mm. 图2 (a) 为采用二维分段函数拟合的半个激光形貌的纵剖面,函数表达式如下 ...
高速轮轨黏着特性数值分析. [硕士论文]
1
2009
... 计算表明,(1) 在水润滑状态下,随机形貌以及纵纹、横纹、菱形对应的轮轨黏着系数都随速度的增大而降低(图8 和图9 只显示 蠕滑率分别为0.3% 和2.0% 的两情况). 这与油润滑或其他液体润滑的结果是一致的,即:流体动压随速度的增大而增大,膜厚增大,因而,黏着系数减小. (2) 蠕滑率$s$的变化对黏着系数的影响不大,如图10 (图中仅显示了300 km/h 时的情况). 这是因为本文的计算没有考虑接触摩擦热导致的温度的变化,这与文献[33 ] 的结果是一致的. 如果考虑接触摩擦热使轮轨接触区温度升高,则对应的黏着系数都减小[20 ] . 无论是干接触态还是润滑态,各种实验结果都显示,当蠕滑率增大到一定程度时,黏着系数有一个峰值,过了峰值之后, 黏着系数将随蠕滑率的增大而减小[34 -38 ] . 因为在实验中,接触摩擦热是必定存在的. ...
高速轮轨黏着特性数值分析. [硕士论文]
1
2009
... 计算表明,(1) 在水润滑状态下,随机形貌以及纵纹、横纹、菱形对应的轮轨黏着系数都随速度的增大而降低(图8 和图9 只显示 蠕滑率分别为0.3% 和2.0% 的两情况). 这与油润滑或其他液体润滑的结果是一致的,即:流体动压随速度的增大而增大,膜厚增大,因而,黏着系数减小. (2) 蠕滑率$s$的变化对黏着系数的影响不大,如图10 (图中仅显示了300 km/h 时的情况). 这是因为本文的计算没有考虑接触摩擦热导致的温度的变化,这与文献[33 ] 的结果是一致的. 如果考虑接触摩擦热使轮轨接触区温度升高,则对应的黏着系数都减小[20 ] . 无论是干接触态还是润滑态,各种实验结果都显示,当蠕滑率增大到一定程度时,黏着系数有一个峰值,过了峰值之后, 黏着系数将随蠕滑率的增大而减小[34 -38 ] . 因为在实验中,接触摩擦热是必定存在的. ...
Twin disc assessment of wheel-rail adhesion
1
2008
... 计算表明,(1) 在水润滑状态下,随机形貌以及纵纹、横纹、菱形对应的轮轨黏着系数都随速度的增大而降低(图8 和图9 只显示 蠕滑率分别为0.3% 和2.0% 的两情况). 这与油润滑或其他液体润滑的结果是一致的,即:流体动压随速度的增大而增大,膜厚增大,因而,黏着系数减小. (2) 蠕滑率$s$的变化对黏着系数的影响不大,如图10 (图中仅显示了300 km/h 时的情况). 这是因为本文的计算没有考虑接触摩擦热导致的温度的变化,这与文献[33 ] 的结果是一致的. 如果考虑接触摩擦热使轮轨接触区温度升高,则对应的黏着系数都减小[20 ] . 无论是干接触态还是润滑态,各种实验结果都显示,当蠕滑率增大到一定程度时,黏着系数有一个峰值,过了峰值之后, 黏着系数将随蠕滑率的增大而减小[34 -38 ] . 因为在实验中,接触摩擦热是必定存在的. ...
An experimental investigation of transient traction characteristics in rolling-sliding wheel-rail contacts under dry-wet conditions
Sub-scale simulation and measurement of railroad wheel/rail adhesion under dry and wet conditions
2013
The role of slip ratio in rolling contact fatigue of rail materials under wet conditions
2017
Effect of oil and water mixtures on adhesion in the wheel-rail contact
1
2009
... 计算表明,(1) 在水润滑状态下,随机形貌以及纵纹、横纹、菱形对应的轮轨黏着系数都随速度的增大而降低(图8 和图9 只显示 蠕滑率分别为0.3% 和2.0% 的两情况). 这与油润滑或其他液体润滑的结果是一致的,即:流体动压随速度的增大而增大,膜厚增大,因而,黏着系数减小. (2) 蠕滑率$s$的变化对黏着系数的影响不大,如图10 (图中仅显示了300 km/h 时的情况). 这是因为本文的计算没有考虑接触摩擦热导致的温度的变化,这与文献[33 ] 的结果是一致的. 如果考虑接触摩擦热使轮轨接触区温度升高,则对应的黏着系数都减小[20 ] . 无论是干接触态还是润滑态,各种实验结果都显示,当蠕滑率增大到一定程度时,黏着系数有一个峰值,过了峰值之后, 黏着系数将随蠕滑率的增大而减小[34 -38 ] . 因为在实验中,接触摩擦热是必定存在的. ...
The draining of a vertical plate
1
1930
... 关于表面形貌取向对黏着系数的影响,存在不同的、甚至是相互矛盾的研究结果. Akbarzadeh 根据从Jeffreys 方程推导出的Moes 模型计算得到的结果是:横纹的黏着系数大于纵纹的黏着系 数[39 -42 ] . 这个模拟方法既没有设定接触区的形状,也没有“流量恒定” 这个假设. Zhu 等[43 ] 用统一雷诺方程模型系统地研究了从线接触到点接触、从低速到高速、从边界润滑到全膜润滑的各种情 况下表面形貌取向对膜厚比($\gamma$) 的影响规律,结论是:在混合润滑条件下($0.05 < \gamma < 1.0$),对于线接触和点接触椭圆率$k > 1$的情况,侧流效应可忽略,因而,横纹的膜厚比大于纵纹的膜厚比,相当于横纹 黏着系数小于纵纹黏着系数;对于点接触椭圆率$k < 1$的情况,侧流效应不能忽略,因而,纵纹的膜厚比大于横纹的膜厚比,相当于纵纹黏着系数小于横纹黏着系数. 这说明,平均流量模型所假设的接触区流量恒定只对于线接触和点接触中椭圆率$k \gg 1$的情况适用,对于$k \ll 1$和$k \approx 1$的情况,平均流量模型可能导致谬误. ...
Optimum similarity analysis with applications to elastohydrodynamic lubrication
1992
Effect of surface pattern on Stribeck curve
2010
On the prediction of running in behavior in mixed-lubrication line contact
1
2010
... 关于表面形貌取向对黏着系数的影响,存在不同的、甚至是相互矛盾的研究结果. Akbarzadeh 根据从Jeffreys 方程推导出的Moes 模型计算得到的结果是:横纹的黏着系数大于纵纹的黏着系 数[39 -42 ] . 这个模拟方法既没有设定接触区的形状,也没有“流量恒定” 这个假设. Zhu 等[43 ] 用统一雷诺方程模型系统地研究了从线接触到点接触、从低速到高速、从边界润滑到全膜润滑的各种情 况下表面形貌取向对膜厚比($\gamma$) 的影响规律,结论是:在混合润滑条件下($0.05 < \gamma < 1.0$),对于线接触和点接触椭圆率$k > 1$的情况,侧流效应可忽略,因而,横纹的膜厚比大于纵纹的膜厚比,相当于横纹 黏着系数小于纵纹黏着系数;对于点接触椭圆率$k < 1$的情况,侧流效应不能忽略,因而,纵纹的膜厚比大于横纹的膜厚比,相当于纵纹黏着系数小于横纹黏着系数. 这说明,平均流量模型所假设的接触区流量恒定只对于线接触和点接触中椭圆率$k \gg 1$的情况适用,对于$k \ll 1$和$k \approx 1$的情况,平均流量模型可能导致谬误. ...
Effect of roughness orientation on the elastohydrodynamic lubrication film thickness
1
2013
... 关于表面形貌取向对黏着系数的影响,存在不同的、甚至是相互矛盾的研究结果. Akbarzadeh 根据从Jeffreys 方程推导出的Moes 模型计算得到的结果是:横纹的黏着系数大于纵纹的黏着系 数[39 -42 ] . 这个模拟方法既没有设定接触区的形状,也没有“流量恒定” 这个假设. Zhu 等[43 ] 用统一雷诺方程模型系统地研究了从线接触到点接触、从低速到高速、从边界润滑到全膜润滑的各种情 况下表面形貌取向对膜厚比($\gamma$) 的影响规律,结论是:在混合润滑条件下($0.05 < \gamma < 1.0$),对于线接触和点接触椭圆率$k > 1$的情况,侧流效应可忽略,因而,横纹的膜厚比大于纵纹的膜厚比,相当于横纹 黏着系数小于纵纹黏着系数;对于点接触椭圆率$k < 1$的情况,侧流效应不能忽略,因而,纵纹的膜厚比大于横纹的膜厚比,相当于纵纹黏着系数小于横纹黏着系数. 这说明,平均流量模型所假设的接触区流量恒定只对于线接触和点接触中椭圆率$k \gg 1$的情况适用,对于$k \ll 1$和$k \approx 1$的情况,平均流量模型可能导致谬误. ...