引言

水平井多段压裂是开发低渗透油气藏、页岩气藏和致密气藏等非常规油气藏的有效方法^[1,2]。压裂的设计、压裂后裂缝参数的获取和压裂效果的评价是水平井多段压裂需要解决的问题^[3]。试井测试是评价压裂效果和获取裂缝及储层参数的重要手段。

1993年,Guo和Evans^[4,5,6,7]建立了一种均匀流量裂缝的多段压裂水平井模型,该模型假设流体只能通过裂缝流入井筒,不考虑水平井筒的流动阻力,因此可以简化为二维问题。采用格林函数、源函数和叠加原理,得到了多裂缝压裂水平井的井底压力解。该模型采用流量平均的假设对于井底压力响应的分析精度不够,且没有考虑裂缝间的流动干扰,只能适用于早期流动描述。1994年,Larsen和Hegre^[8]建立了有限导流能力裂缝模型的多裂缝压力水平井模型,裂缝的处理采用Cinco-Ley^[9]处理有限导流能力裂缝的方法。该模型得到多裂缝水平井井底压力响应的四个流动阶段：裂缝径向流、径向-线性流、底层线性流和系统径向流。1995年,Horne和Temeng^[10]采用格林函数和源函数方法建立了考虑井筒储存、表皮效应和裂缝间干扰的均匀流量多裂缝压裂水平井模型。对于无井储的情况,该模型得到的井底压力响应可以分为四个阶段：第一线性流、第一拟径向流、第二线性流和第二拟径向流。1991年,Ozkan和Raghavan^[11]给出了考虑不同井类型、不同边界类型、不同油藏类型的广泛解。1997年,Chen和Raghavan^[12]建立了矩形油藏中多段压裂水平井的试井模型,采用Ozkkan和Raghavan基本点源解,其裂缝处理方法与Horne和Temeng的方法类似,但其裂缝为有限导流裂缝。该模型的流动段划分与Horne和Temeng相比多了早期的双线性流。2009年,Ozkan和Brown^{[13, 14]}等人提出三线性流模型,该模型计算简单,但无法表征压裂水平井的各个流动阶段。

1996年,国内的李笑萍^[15]最早研究了压裂水平井井底压力响应动态特征,其模型的裂缝为有限导流裂缝,采用积分变换方法获得井底压力解,但其没有考虑井筒储存和表皮效应。2011年,姚军^[16]等利用三线性流模型研究了低渗透具有启动压力梯度的压裂水平井井底压力动态响应,分析启动压力梯度、裂缝导流能力、裂缝间距、裂缝储能等因素的影响。2013年,王本成^[17]等建立了综合考虑无限导流能力裂缝、裂缝倾角、裂缝间距不等、裂缝纵向未完全贯穿地层等多重情况建立了多段压裂水平井的解析试井模型。利用源函数理论、三维特征值和正交变化等分析方法对模型进行了求解。2014年,王晓冬等^[18]通过确定导流能力影响函数,给出了有限导流垂直裂缝井不稳定渗流的解析解,再利用叠加原理得到了多段压裂水平井的不稳定压力分析模型,模型计算结果表明,试井曲线表现的流动特征是早期双线性流-早期线性流-中期径向流-中期线性流-晚期拟径稳态流。2014年,欧阳伟平^[19,20]等建立了无限导流能力裂缝的压裂水平井数值试井模型,模型考虑了水平井筒的流量,分析了不同裂缝条数下的射孔产率比,得到了最佳压裂段数的计算公式。孙致学和姚军^[21]等人基于离散裂缝模型研究了复杂裂缝系统的水平井动态特征,研究了分支裂缝对井底压力动态特征的影响。许多其他学者也都针对不同的压裂水平井特征建立了试井模型^{[22,23,24,25,26,27,28]},分析了水平井的流动阶段。

目前的压裂水平井的研究方法多以解析解为主,而解析解只能处理简单的裂缝情况,目前多数的多段压裂水平井模型未能考虑到裂缝间的干扰对试井理论曲线的影响。实际水力压裂产生的裂缝是非常复杂的,裂缝不对称、裂缝长度不等、某段压裂失败造成裂缝缺失等情况都可能存在。对于这些复杂裂缝情况,只能采用数值解的方法建立数值试井模型进行描述。本文基于离散裂缝模型,建立了复杂裂缝情况的多段压裂水平井数值试井模型,得到了多段压裂水平井试井理论曲线和压力场分布,分析了裂缝不等长、裂缝不对称、裂缝导流能力等因素对试井理论曲线的影响,给出压裂设计时需考虑的因素。基于建立的模型,对现场一口多段压裂水平井气井压力恢复测试的数据进行了试井解释,获得了裂缝和储层参数。

1 物理模型

为建立数学模型,作如下假设：

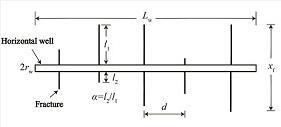
1）考虑二维情况,储层均质。水平井筒长度L_w,井筒半径r_w。裂缝间距相等为d,裂缝全长x_f,裂缝不等长,关于井筒不对称,裂缝的不对称系数为α,α定义为井筒两边短裂缝与长裂缝的比值。裂缝为有限导流裂缝,其渗透率为K_f,宽度为e,裂缝条数为n。基于离散裂缝模型,将裂缝简化为线,其宽度e不体现在物理模型当中。模型示意图如图1所示。

2）储层中流体为弱可压缩、定常黏度的单相牛顿流体,流体在储层中流动状态为层流,符合达西定律。

3）假设井筒具有无限大导流能力,即流体在井筒中流动没有阻力,水平井井筒的压力处处相等。

显示原图| 下载原图ZIP| 生成PPT

图1   多段压裂水平井物理模型示意图

Fig.1   Conceptual model of multi-fractured horizontal well

2 数学模型及其求解

2.1 数学模型

由于裂缝宽度较小,其数量级通常是毫米量级。因此,如果基于真实的裂缝宽度建立几何模型进行网格划分,则网格数量大,网格质量差,计算中可能存在震荡和不收敛情况。为简化裂缝建模,利用离散裂缝模型,忽略裂缝中垂直于裂缝方向的流动,将裂缝中的流动简化为一维,裂缝采用线来描述^[29,30]。

系统的控制方程在离散裂缝模型简化前可表示为：

$\int_{\Omega }{\text{FEQ}}\text{d}\Omega =\int_{{{ \Omega }_{\text{m}}}}{\text{FEQd}{{ \Omega }_{\text{m}}}}+\int_{{{ \Omega }_{\text{f}}}}{\text{FEQd}{{ \Omega }_{\text{f}}}}$ （1）

其中,FEQ表示流动控制方程,$\Omega $表示整个研究区域,${{\Omega }_{\text{f}}}$为裂缝区域,${{\Omega }_{\text{m}}}$为基质区域。离散裂缝模型简化之后的控制方程为：

$\int_{\Omega} FEQd \Omega=\int_{\Omega_{m}} FEQ d\Omega_{m} +e \cdot \int_{\Omega '_{f}} FEQ'd \Omega '_{f}$ （2）

${{\Omega }_{\text{f}}}^{\prime }$为离散裂缝模型中裂缝区域。

因此,整个模型的控制方程分为二维的储层区域和一维的裂缝区域。

储层流动控制方程为

$\frac{{{K}_{\text{m}}}}{\mu }\frac{{{\partial }^{2}}{{p}_{\text{m}}}}{\partial {{x}^{2}}}+\frac{{{K}_{\text{m}}}}{\mu }\frac{{{\partial }^{2}}{{p}_{\text{m}}}}{\partial {{y}^{2}}}={{\phi }_{\text{m}}}{{C}_{\text{t}}}\frac{\partial {{p}_{\text{m}}}}{\partial t}$ （3）

其中,K_m储层渗透率, m²;μ为流体粘度,Pa·s;p_m储层压力,Pa;${{\phi }_{\text{m}}}$为储层孔隙度;${{C}_{t}}$为综合压缩系数,Pa^-1;t为时间,s。

裂缝流动控制方程为

$\frac{{{K}_{\text{f}}}}{\mu }\frac{{{\partial }^{2}}{{p}_{\text{f}}}}{\partial {{l}^{2}}}={{\phi }_{\text{f}}}{{C}_{\text{t}}}\frac{\partial {{p}_{\text{f}}}}{\partial t}$ （4）

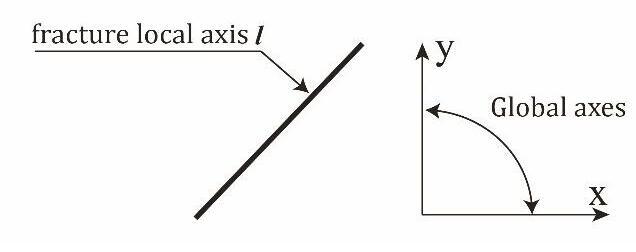
其中,${{p}_{\text{f}}}$为裂缝压力,Pa;K_f为裂缝的渗透率,m²; l为裂缝的一维局部坐标,其与整体坐标的关系如图2所示。

显示原图| 下载原图ZIP| 生成PPT

图2   裂缝局部坐标与全局坐标关系图

Fig.2   Relationship of the local coordinates of fractures and global coordinates

初始条件

${{p}_{\text{m}}}={{p}_{\text{i}}},{{p}_{\text{f}}}={{p}_{\text{i}}}$ （5）

内边界条件

${{\left. -\sum\limits_{j=1}^{N}{{{L}_{j}}h}\frac{K}{\mu }\frac{\partial {{p}_{j}}}{\partial n} \right|}_{{{\Gamma }_{i}}}}=Bq+C\frac{d{{p}_{\text{w}}}}{dt}$ （6）

${{p}_{j}}={{p}_{\text{w}}}$ （7）

外边界条件

定压边界：${{\left. p \right|}_{{{\Gamma }_{o}}}}={{p}_{\text{i}}}$ （8）

或

封闭边界：${{\left. \frac{\partial p}{\partial n} \right|}_{{{\Gamma }_{o}}}}=0$ （9）

其中,p_i为原始地层压力,Pa;L_j井筒内边界上离散单元的边长,m;h为储层有效厚度,m;B为流体体积系数,m³/m³;q为井筒的总流量,m³/s;C井筒储存系数,m³/Pa;p_w为井底压力,Pa;N为内边界离散单元的边数。

2.2 有限元方法求解

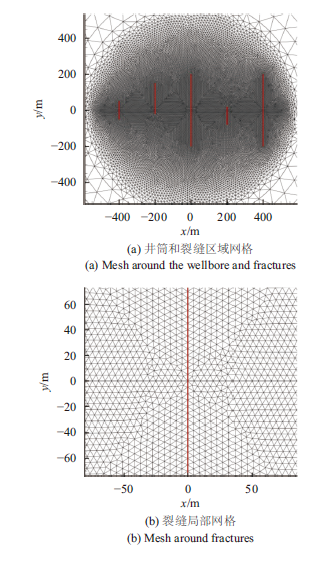
利用有限元方法求解模型,首先需要对模型进行网格剖分。图3是有限元计算使用的网格图。储层采用二维三角形单元离散,裂缝采用一维线单元离散。由于井筒和裂缝附近压力梯度很大,为提高计算精度,在水平井筒和裂缝附近进行局部网格加密。

显示原图| 下载原图ZIP| 生成PPT

图3   储层和裂缝网格图

Fig.3   Mesh of the physical model

在图3所示的二维三角形单元和一维线单元上推导有限元方程。采用Garlerkin加权余量法,可得储层流动控制方程的Garlerkin方程为

$\iint_{A}{\left( \frac{{{K}_{\text{m}}}}{\mu }\frac{{{\partial }^{2}}p_{_{\text{m}}}^{\text{e}}}{\partial {{x}^{2}}}+\frac{{{K}_{\text{m}}}}{\mu }\frac{{{\partial }^{2}}p_{_{\text{m}}}^{\text{e}}}{\partial {{y}^{2}}}+{{\phi }_{\text{m}}}{{C}_{\text{t}}}\frac{\partial p_{_{\text{m}}}^{\text{e}}}{\partial t} \right)\delta p_{_{\text{m}}}^{\text{e}}}dA=0$（10）

其弱形式为

$\begin{align} \iint_{A}{\left( \frac{{{K}_{\text{m}}}}{\mu }\frac{\partial p_{_{\text{m}}}^{\text{e}}}{\partial x}\frac{\partial \delta p_{_{\text{m}}}^{\text{e}}}{\partial x}+\frac{{{K}_{\text{m}}}}{\mu }\frac{\partial p_{_{\text{m}}}^{\text{e}}}{\partial y}\frac{\partial \delta p_{_{\text{m}}}^{\text{e}}}{\partial y}+{{\phi }_{\text{m}}}{{C}_{\text{t}}}\frac{\partial p_{_{\text{m}}}^{\text{e}}}{\partial t}\delta p_{_{\text{m}}}^{\text{e}} \right)}dA =\int_{s}{\delta p_{_{\text{m}}}^{\text{e}}\frac{{{K}_{\text{m}}}}{\mu }\frac{\partial p_{_{\text{m}}}^{\text{e}}}{\partial n}}ds \\ \end{align}$ (11)

其中$p_{_{m}}^{e}$为储层网格单元压力,表达式为

$p_{_{\text{m}}}^{\text{e}}={{N}_{\text{m}i}}p_{\text{m}i}^{\text{e}}+{{N}_{\text{m}j}}p_{\text{m}j}^{\text{e}}+{{N}_{\text{m}k}}p_{\text{m}k}^{\text{e}}$ （12）

$p_{\text{m}i}^{\text{e}}$、$p_{\text{m}j}^{\text{e}}$、$p_{\text{m}k}^{\text{e}}$为单元结点上的压力值。

${{N}_{\text{m}}}$为单元线性插值函数,表达式为

${{N}_{\text{m}j}}={{a}_{j}}+{{b}_{j}}x+{{c}_{j}}y$ （13）

将（12）式和（13）式代入（11）式,可得储层有限元单元刚度方程为

$\begin{align}A\left( \frac{{{K}_{\text{m}}}}{\mu }b_{i}^{2}+\frac{{{K}_{\text{m}}}}{\mu }c_{i}^{2}+\frac{{{\phi }_{\text{m}}}{{C}_{\text{t}}}}{6\Delta t} \right)p_{\text{m}i}^{\text{e},n+1}+A\left( \frac{{{K}_{\text{m}}}}{\mu }{{b}_{i}}{{b}_{j}}+\frac{{{K}_{\text{m}}}}{\mu }{{c}_{i}}{{c}_{j}}+\frac{{{\phi }_{\text{m}}}{{C}_{\text{t}}}}{12\Delta t} \right)p_{\text{m}j}^{\text{e},n+1}+ \\A\left( \frac{{{K}_{\text{m}}}}{\mu }{{b}_{i}}{{b}_{k}}+\frac{{{K}_{\text{m}}}}{\mu }{{c}_{i}}{{c}_{k}}+\frac{{{\phi }_{\text{m}}}{{C}_{\text{t}}}}{12\Delta t} \right)p_{\text{m}k}^{\text{e},n+1}-\frac{L}{3}\frac{\partial p_{\text{m}i}^{\text{e},n+1}}{\partial n}-\frac{L}{6}\frac{\partial p_{\text{m}\left( j,k \right)}^{\text{e},n+1}}{\partial n}= \\\frac{{{\phi }_{\text{m}}}{{C}_{\text{t}}}}{6\Delta t}p_{\text{m}i}^{\text{e},n}+\frac{{{\phi }_{\text{m}}}{{C}_{\text{t}}}}{12\Delta t}p_{\text{m}j}^{\text{e},n}+\frac{{{\phi }_{\text{m}}}{{C}_{\text{t}}}}{12\Delta t}p_{\text{m}k}^{\text{e},n} \\ \end{align}$ （14）

裂缝单元弱形式的流动控制方程为

$\begin{align} \int_{l}{\left( \frac{{{K}_{\text{f}}}}{\mu }\frac{\partial p_{_{\text{f}}}^{\text{e}}}{\partial l}\frac{\partial \delta p_{\text{f}}^{\text{e}}}{\partial l}+{{\phi }_{\text{f}}}{{C}_{\text{t}}}\frac{\partial p_{_{\text{f}}}^{\text{e}}}{\partial t}\delta p_{\text{f}}^{\text{e}} \right)}\delta p_{\text{f}}^{\text{e}}dl =\left. \delta p_{\text{f}}^{\text{e}}\frac{{{K}_{\text{f}}}}{\mu }\frac{\partial p_{_{\text{f}}}^{\text{e}}}{\partial l} \right|_{1}^{2} \\ \end{align}$ （15）

其中$p_{\text{f}}^{\text{e}}$裂缝单元压力,表达式为

$p_{_{\text{f}}}^{\text{e}}={{N}_{\text{f}i}}p_{\text{f}i}^{\text{e}}+{{N}_{\text{f}j}}p_{\text{f}j}^{\text{e}}$ （16）

$p_{\text{f}i}^{\text{e}}$、

$p_{\text{f}j}^{\text{e}}$

为裂缝单元上结点的压力值。

${{N}_{\text{f}}}$为裂缝单元的插值函数,表达式为

${{N}_{\text{f}i}}=\frac{{{l}_{j}}-l}{{{L}_{\text{f}}}},{{N}_{\text{f}j}}=\frac{l-{{l}_{i}}}{{{L}_{\text{f}}}}$ （17）

将（16）式和（17）式代入（15）式可得裂缝有限元单元刚度方程为

$\begin{align} (\frac{{{K}_{\text{f}}}}{\mu }\frac{1}{{{L}_{\text{f}}}}+\frac{{{\phi }_{\text{f}}}{{C}_{\text{t}}}}{3\Delta t})p_{\text{f}i}^{\text{e},n+1}+(-\frac{{{K}_{\text{f}}}}{\mu }\frac{1}{{{L}_{\text{f}}}}+\frac{{{\phi }_{\text{f}}}{{C}_{\text{t}}}}{3\Delta t})p_{\text{f}j}^{\text{e},n+1} =\frac{{{\phi }_{\text{f}}}{{C}_{\text{t}}}}{3\Delta t}p_{\text{f}i}^{\text{e},n}+\frac{{{\phi }_{\text{f}}}{{C}_{\text{t}}}}{6\Delta t}p_{\text{f}j}^{\text{e},n} \\ \end{align}$（18）

从上式可知,裂缝流动控制方程经有限元方法离散后,空间变量（即裂缝局部坐标）变为裂缝单元的长度,而裂缝单元的长度是已知的。因此,不需要将裂缝的局部坐标向全局坐标进行转换。

由内边界流量之和等于产量可得：

${{\left. \sum\limits_{j=1}^{N}{{{L}_{j}}h}\frac{K}{\mu }\frac{\partial p_{_{j}}^{n+1}}{\partial n} \right|}_{{{\Gamma }_{i}}}}+\frac{p_{\text{w}}^{n+1}}{\Delta t}=-Bq+C\frac{p_{\text{w}}^{n}}{\Delta t}$ (19)

内边界各点压力相等,可得：

${{p}_{j}}={{p}_{\text{w}}}$ (20)

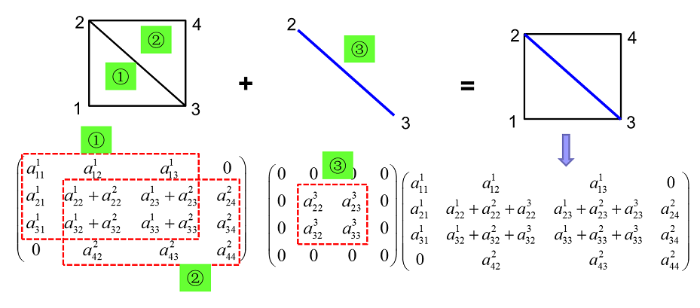
联立(14)式、(18)式、(19)式、(20)式,根据结点编号规则,将裂缝线单元刚度方程和储层面单元刚度方程组装成总体刚度方程,其组装方式如图4所示 ^[31,32]。利用SuperLU^[33,34]求解有限元总体刚度方程可得各时刻网格结点的压力值。

显示原图| 下载原图ZIP| 生成PPT

图4   三角形单元和线单元的叠加处理过程图（1,2,3,4为结点编号;①,②为储层三角形单元,③为裂缝线单元）

Fig.4   The superposition process of triangle elements and line elements. (1,2,3,4 are the node number, ①, ② are triangle elements, ③ is a line element)

3 计算结果及分析

3.1 井底压力响应曲线及储层压力扩散特征

利用有限元方法对建立的模型进行求解,为分析其井底压力响应特征,先考虑裂缝等长、关于井筒对称且等间距的情况。图5为该情况下的底压力响应曲线,从曲线特征上可以看出,井底流动可以分为7个阶段：

显示原图| 下载原图ZIP| 生成PPT

图5   多段压裂水平井试井理论曲线

Fig.5   Well test type curves of the multi-fractured horizontal wells

（1）井筒储存阶段。该阶段主要反映井筒流体压缩特征,压力和压力导数呈现斜率为1的直线。

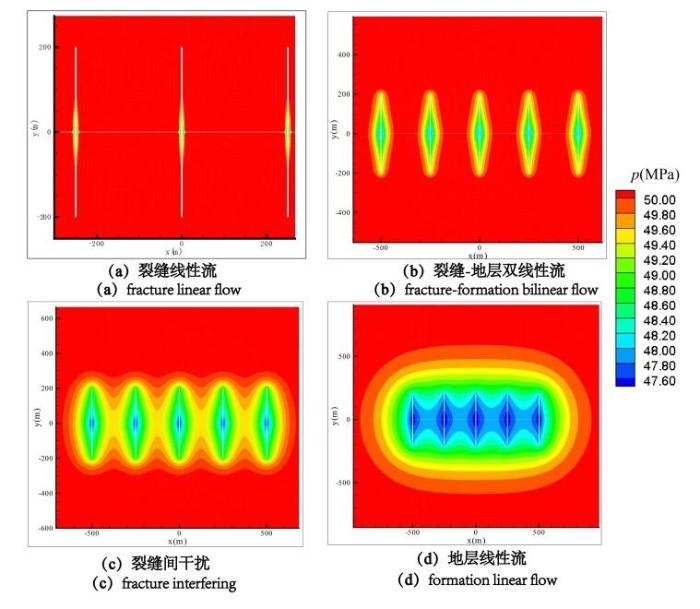
（2）裂缝线性流阶段。本文模型假设裂缝为有限导流能力裂缝,因此,在井筒储存系数较小情况下,在流动到达裂缝端部以前,流体沿着裂缝向井筒流动,形成裂缝的线性流动阶段。如图6-(a)所示。压力和压力导数曲线表现为斜率为1/2的平行线。

显示原图| 下载原图ZIP| 生成PPT

图6   多段压裂水平井的压力场扩展特征

Fig.6   Pressure field of the multi-fractured horizontal well

（3）裂缝-地层双线性流动阶段。流体沿裂缝向井筒流动,同时地层中流体向裂缝流动,形成裂缝-地层的双线性流,其压力分布如图6-(b)所示。该阶段的压力和压力导数平行,斜率为1/4.

（4）裂缝干扰阶段。随着压力扩展,相邻裂缝之间的压力产生相互干扰,压力导数开始上翘,压力和压力导数之间的距离减小。从图6-(c)所示的压力场图可以看出,裂缝之间的压力等直线开始关联,表明流动受裂缝之间相互干扰。

（5）地层线性流阶段。压力继续向外扩展,流体形成垂直于水平井筒且平行于裂缝面的线性流动,压力场如图6-(d)所示。该阶段的压力和压力导数表现为斜率等于1/2的平行线。

（6）系统径向流阶段。压力扩展到远处时,整个压裂水平井可以看作一个点,流体的流程整体上呈现出径向流动。此时压力导数为水平线直线。

（7）边界反映段。当压力扩展到达封闭边界时,

逐渐过渡到拟稳态流动,压力和压力导数开始上翘,最终两者均为斜率为1的直线。

需要说明的是,以上各个流动阶段并不是全部都可以在试井理论曲线上表现出来,在某些参数组合下,许多特征都会被其他特征掩盖。例如,井筒储存系数较大时,井筒储存效应会掩盖裂缝的线性流;裂缝间距离较小的情况下,裂缝间流动干扰可能会掩盖地层-裂缝双线性流。但整体上多段压裂水平井表现出的主要特征是线性流特征。

3.2 裂缝数量对试井理论曲线的影响

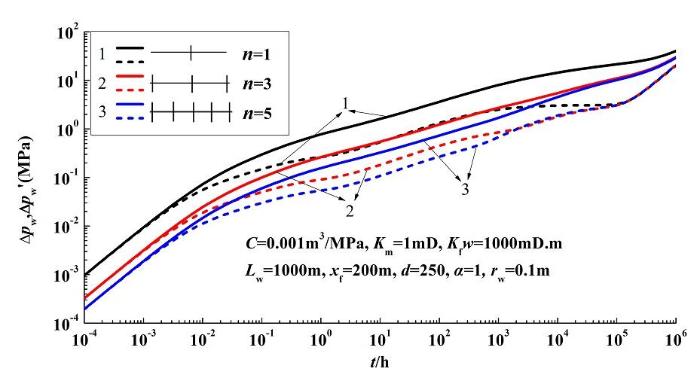
图7是裂缝条数分别为1条、3条和5条情况下的试井理论曲线。从图可以看出,裂缝条数越多,裂缝间距越小,裂缝间出现干扰的时间越早,干扰幅度越大,曲线上表现为压力导数越早偏移双线性流,偏离幅度越大;裂缝条数多井底压力值远大于裂缝条数少的井底压力值,说明相同产量下,裂缝越多,井底压降越小,即井筒的流动阻力越小。

显示原图| 下载原图ZIP| 生成PPT

图7   不同裂缝数量的多段压裂水平井试井理论曲线

Fig.7   Well test type curves at different numbers of fractures

3.3 裂缝间距对试井理论曲线的影响

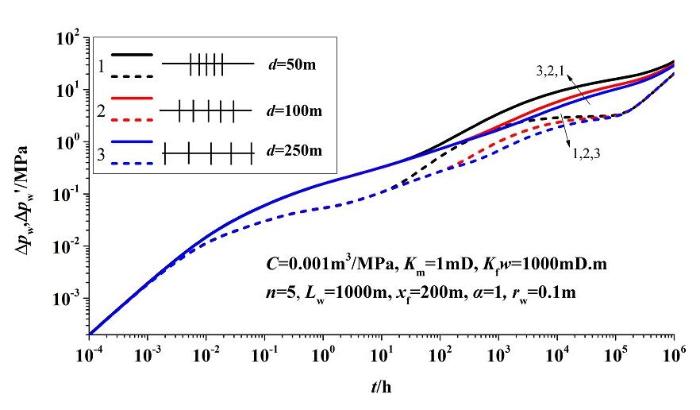
图8是不同裂缝间距下的试井理论曲线。裂缝间距分别为50m、100m和250m。从图可以看出,裂缝间距主要影响试井理论曲线的第三阶段,即裂缝干扰段。裂缝间距越小,干扰出现越早,干扰程度越大,曲线上表现为压力导数越早偏离1/2斜率线,且偏离幅度越大。裂缝间距小的井底压力值比裂缝间距大的井底压力值大,说明裂缝间距越大,改造的储层范围越大,井底流动阻力越小。因此,当确定了压裂段数后,应尽量使各压裂段之间的距离最大。

显示原图| 下载原图ZIP| 生成PPT

图8   不同裂缝间距的多段压裂水平井试井理论曲线

Fig.8   Well test type curves at different spacing of fractures

3.4 裂缝间距对试井理论曲线的影响

图9是裂缝不对称情况下的试井理论曲线。各组曲线的裂缝全长x_f相同,裂缝的不对称系数依次为1/19、1/3和1。从图可知,裂缝不对称主要影响裂缝线性流段和裂缝-地层双线性流段,裂缝的不对称程度越大,裂缝线性流段持续时间越长,且由于裂缝不对称的影响,裂缝-地层双线性流段的早期压力导数斜率偏小。裂缝对称情况下压力值比裂缝不对称的压力值小,说明裂缝对称时井底流动阻力小,因此,在压裂施工过程中应尽量保证裂缝对称,以减小井底的流动阻力,提高产能。

显示原图| 下载原图ZIP| 生成PPT

图9   不对称裂缝的多段压裂水平井试井理论曲线

Fig.9   Well test types curves of asymmetrical fractures

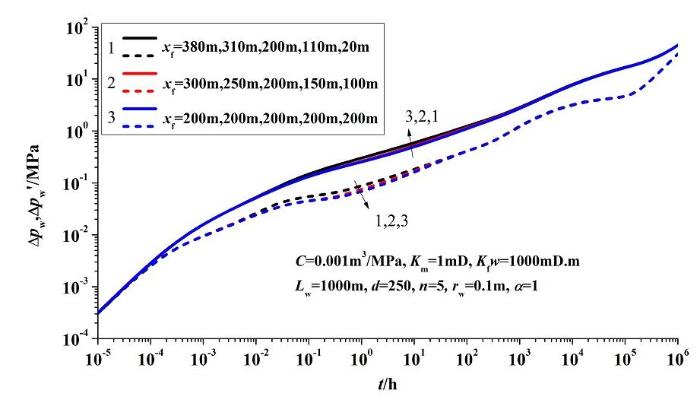
3.5 裂缝不等长对试井理论曲线的影响

图10是裂缝不等长情况下的试井理论曲线。三组曲线均为5条裂缝,裂缝总长度均为1000m。三组曲线的裂缝长度分别为：380m按线性递减到20m、300m按线性递减到100m和等长100m。从图可知,裂缝长度不等时同样影响裂缝的线性流段和裂缝-地层双线性流段。在裂缝总长一样的情况下,裂缝等长时井底的流动阻力小于裂缝不等长,因此压裂时建议尽量保证裂缝等长,但裂缝不等长对试井理论曲线的影响比裂缝的不对称要小得多。

显示原图| 下载原图ZIP| 生成PPT

图10   不等长裂缝的多段压裂水平井试井理论曲线

Fig.10   Well test types curves at different length of fractures

3.6 部分裂缝缺失对试井理论曲线的影响

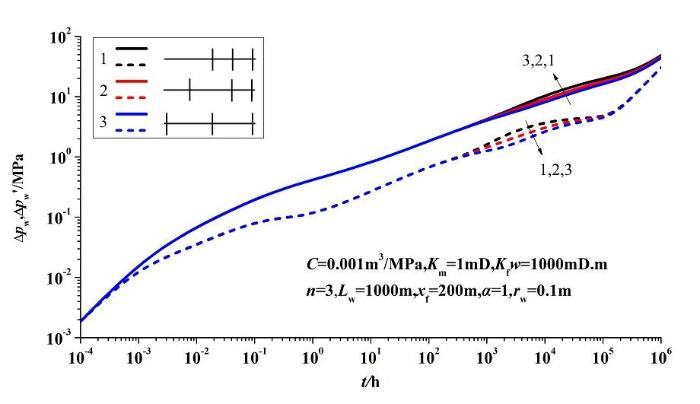
压裂施工过程中,可能某些压裂段压裂不成功,不能在水平井筒的某些位置形成有效裂缝。图11是进行五段压裂水平井中两段压裂失效情况下的试井理论曲线,其中曲线1裂缝失效位置为从左至右的第1段和第2段,曲线2裂缝失效位置为第1段和第3段,曲线3裂缝失效位置为第2段和第3段。由图可知,在裂缝参数一样,缺失裂缝数量一样的情况下,裂缝缺失对试井理论曲线的影响主要反映在裂缝干扰段和裂缝地层线性流段。某段裂缝缺失后,裂缝间距发生变化,造成裂缝间的干扰程度不一样,其对试井的影响与裂缝间距类似。多段压裂水平井进行试井解释时,可以结合压裂施工的过程,进一步验证裂缝的失效情况。

显示原图| 下载原图ZIP| 生成PPT

图11   部分裂缝缺失情况的多段压裂水平井试井理论曲线

Fig.10   Well test types curves of some fractures lost.

4 实例分析

利用多建立的数值试井模型对四川盆地多口压裂水平井进行了试井解释,以其中一口井A为例说明试井解释的过程和结果。A井的基础参数如表1所示。

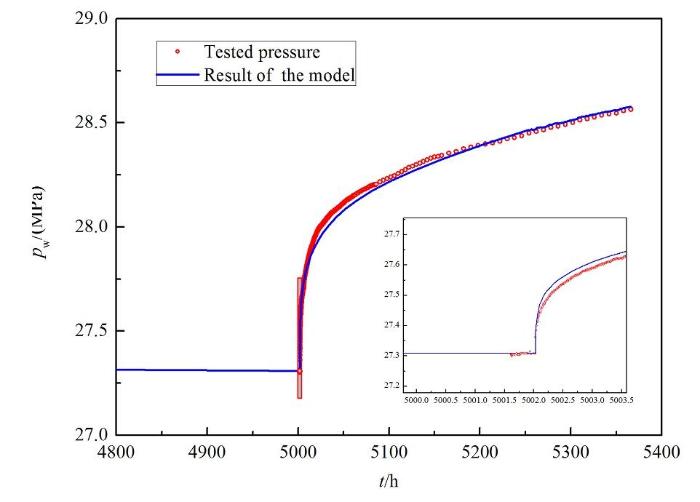
该井进行了压力恢复测试,关井前以9.1×10⁴m³/d的产量生产201天,关井约363.97小时。压力恢复测试的压力历史图如图12所示。A井本次测试关井时测点流压为27.35MPa,关井约363.97小时,压力恢复至28.61MPa,恢复幅度为1.26MPa;实测关井压力恢复曲线直观反映：整个关井压力恢复过程恢复缓慢,后期压力仍然呈上升趋势,表明储层整体的渗流能力较差。

显示原图| 下载原图ZIP| 生成PPT

图12   A井压力恢复历史拟合图

Fig.12   The pressure history matching of well-A.

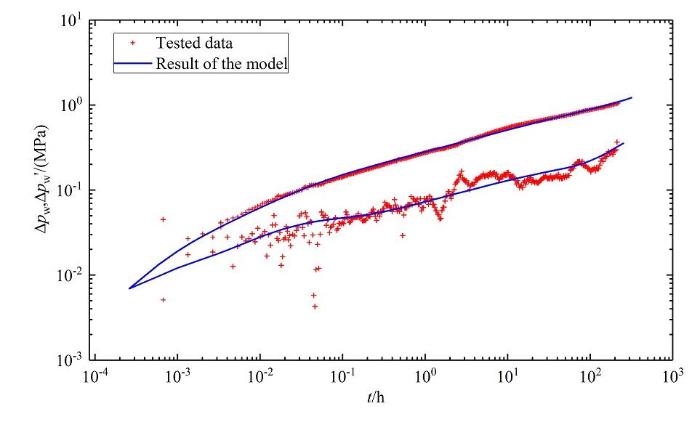
做出压力恢复的双对数压力和压力导数曲线,如图13所示。从图可以看出,A井的压力恢复双对数曲线特征主要是线性流段,与本文建立的模型相符。

显示原图| 下载原图ZIP| 生成PPT

图13   A井压力恢复测试双对数曲线拟合图

Fig.13   The log-log type curves matching of well A.

该井分17段进行了水力加砂压裂,整个压裂过程消耗的总液量26905.18m³、总砂量934.50m³,各段加砂量见表2。数值试井解释过程中,需要先建立

储层的几何模型,即需要已知裂缝的位置及裂缝长度信息,同时为了提高拟合效率和拟合精度,也需要给定裂缝几何参数的初始值。裂缝长度的初始值利用下面的公式由加砂量估算：

${{V}_{p}}=\frac{\pi }{5}{{x}_{f}}{{w}_{f}}{{h}_{w}}$ (22)

其中,V_p为总砂量;x_f为裂缝长度;w_f为近井地带裂缝宽度,取值8mm;h_w为裂缝垂向高度,取储层的厚度。该公式的计算方法即认为加入的砂填满整个裂缝,裂缝形态为一定厚度的椭圆。利用该公式初步计算裂缝的半长,如表2所示。从表中计算结果可以看出,用该方法估算的裂缝长度基本在100m左右,其中第10段裂缝长度偏小的原因是未加入线性胶,导致加砂量不足。

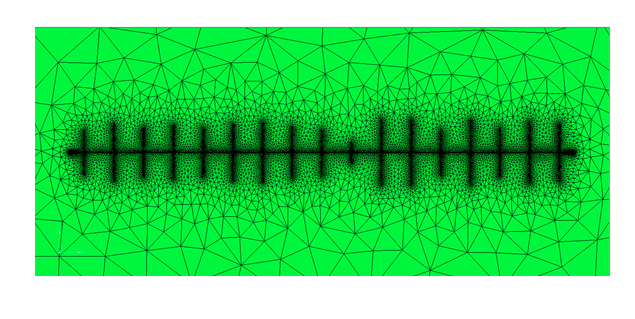
以表2中估算得到的裂缝长度参数为基础,建立几何模型进行网格划分,并在井筒周围及裂缝上对网格进行加密。划分网格如图14所示,网格单元数为25238,网格结点数为13139.

显示原图| 下载原图ZIP| 生成PPT

图14   A井数值试井解释模型网格图

Fig.14   The mesh of the numerical well test model of well-A

以图14所示的网格为基础,利用数值计算获得井底压力的双对数曲线,通过调整渗透率、井筒储存系数、裂缝长度和裂缝导流能力等参数拟合实测双对数曲线。需要指出的是,调整裂缝长度参数后,需要重新进行几何建模和网格划分。最终的双对数曲线拟合图如图13所示,压力历史拟合图如图12所示。解释得到的裂缝参数信息见表2,储层相关参数见表3。从解释结果上看,该井压裂形成的裂缝长度均在100m左右,导流能力也均在100mD·m左右,表明该井压裂效果较好。

5 结论

（1）建立了一种多段压裂水平井的数值试井模型,采用离散裂缝模型对裂缝进行简化,利用有限元方法求解试井模型,得到了多段压裂水平井的试井理论曲线和压力分布场。通过对试井理论曲线和压力场的分析,将多段压裂水平井的流体流动分为了七个阶段：井筒储存段、裂缝线性流段、裂缝-地层双线性流段、裂缝干扰段、地层线性流段、系统径向流段和边界反映段。

（2）裂缝条数对试井理论曲线有较大影响。裂缝条数越多,对储层改造程度越大,试井理论曲线中压力值更小,即井底的流动阻力越小。

（3）裂缝间距主要影响试井理论曲线的裂缝干扰段,裂缝间距越小,干扰段出现的时间越早,干扰幅度越大,且裂缝间距越小,井底流动阻力越大。因此,为减小流动阻力,提高产能,在确定压裂段数的情况下应尽可能增大裂缝间距离。

（4）裂缝关于井筒不对称主要影响早期裂缝的线性流和裂缝-地层双线性流段。相同裂缝长度的条件下,裂缝不对称时的井底流动阻力比裂缝对称时井底流动阻力大。因此,压裂施工时尽可能保证裂缝关于井筒的对称性。

（5）裂缝不等长对试井理论曲线的影响与裂缝关于井筒不对称的影响类似,裂缝间长度差别越大,井底流动阻力也越大。因此,在裂缝总长度一样的情况下,尽量保持裂缝长度一致。但与裂缝关于井筒不对称相比,裂缝不等长的影响要小得多。

（6）部分裂缝缺失对试井理论曲线的影响与裂缝间距类似,可以结合试井解释和压裂施工对裂缝失效情况进行判断。

The authors have declared that no competing interests exist.

参考文献

文献选项

• 原文顺序
• 文献年度倒序
• 文中引用次数倒序
• 被引期刊影响因子