0 引言
近年来,超燃冲压发动机受到了越来越多的关注,关键技术已取得了重大突破[1-5].超燃冲压发动机在高马赫数飞行时,气动加热十分严重,当飞行马赫数为6时,来流总温将达到1700 K以上,燃气温度更是超过2 800 K[6-7].为了获得长时间的持续飞行,冲压发动机燃烧室必须采用主动冷却方式[1, 8-9].
在主动冷却系统中,燃料在喷入燃烧室前通过燃烧室壁面等需要冷却结构中的冷却通道,通过物理和化学反应吸热带走待冷却结构的热量,对冷却结构进行对流冷却[10-11].因此,主动冷却结构防热效率高,可以保证发动机长时间工作.另一方面,由于主动冷却系统结构和边界条件十分复杂,一维或二维简化模型无法准确模拟,需采用三维数值方法进行热、力分析.
常用的热、力分析数值算法包括有限单元法、有限差分法和边界元法等.其中有限单元法[12-14]作为目前使用最为广泛的数值计算方法,可以分析包括主动冷却管道在内的各类复杂结构,但由于有限单元法需要对主动冷却结构整体进行建模和网格剖分,需要的单元、节点多,计算量大,且建模复杂,需要耗费大量人力和时间.有限差分法[15-16]则由于边界条件处理麻烦,建模工作量大,也不适用于这种包含许多管道复杂结构的分析.边界元法[17-19]作为新型的数值计算方法,仅需在结构边界上剖分单元,计算节点少,建模简单,且对于复杂结构有较好的精度[20-22].传统的边界元法在组集系数矩阵时,需要遍及计算域内所有构件的边界节点积分,十分耗时,不利于求解大型复杂问题.高效伟[23]提出的三步变量凝聚法$\!$--$\!$多域边界元法可以将复杂的计算域划分成多个简单区域,只需针对各个简单区域独立组集系数矩阵,然后将域内的独立边界节点变量凝聚到域间的公共边界节点上,最终求解只含公共边界节点变量的方程,方程规模大幅减小,显著提高了边界元法解决大型复杂问题的计算效率.尽管多域边界元法已经可以求解一些复杂问题,但对于主动冷却管道这种内部结构复杂的计算模型,由于其需要划分为许多个计算域,且域间公共边界节点数目也很多,最终求解方程的规模仍然很大,计算十分缓慢.除此之外,由于三步变量凝聚法需要将域内独立边界点变量凝聚到域间的公共边界上,需要在变量凝聚前先处理边界条件,不适用于多种工况的计算分析.
将一个大型复杂结构划分为若干个子结构,先分别确定各子结构的系数矩阵,然后再将子结构装配成整体结构,得到整体结构的系数矩阵,这种结构分析方法称为子结构法[12, 24].本文针对冷却通道阵列排布的主动冷却系统,基于子结构法的思想提出了集成单元边界元算法,仅需针对主动冷却结构中仅含一根冷却通道的胞元结构建立边界元模型,形成具有常规单元性能的集成单元,并对集成单元进行组集,建立总体结构的系统方程组.在组集过程中,采用子结构消去法逐步消去集成单元间公共边界节点变量,最终得到只含最外部边界节点变量的系统方程.由于集成单元系数矩阵只需计算一次,且总系数矩阵只含结构最外部边界节点变量,计算规模大幅减小,计算效率显著提高.本文所述方法的思想类似于传统结构分析中的子结构法,但集成单元的功能与使用又具有传统有限单元、边界单元的特征,便于大型空间周期性结构的快速分析,特别是对管道阵列排布的主动冷却结构非常有效.
1 功能梯度材料边界元法
1.1 边界积分方程推导
假设各向同性功能梯度材料的剪切模量$\mu ({ x})$ 随坐标${x}$变化,泊松比$\nu $为常量,弹性体应力张量$\sigma _{ij}$可以表示成位移梯度$u_{k,l} $ 的函数[25-26]
|
$\sigma _{ij} = \mu ({ x})C_{ijkl}^0 u_{k,l}$
|
(1) |
其中
|
$u_{k,l} = \partial u_k / \partial x_l $
|
(2) |
|
$C_{ijkl}^0 = \frac{2\upsilon }{1-\upsilon }\delta _{ij} \delta _{kl} + \delta _{ik} \delta _{jl} + \delta _{il} \delta _{jk}$
|
(3) |
在不考虑体积力的平衡方程$\sigma _{ij,j} = 0$ 两边乘以权函数 $U_{ij} ({{ x}}^p,{{ x}})$,并在计算域内积分可得
|
$\int_\Omega {U_{ij} ({{ x}}^{\rm p},{{ x}}\sigma _{jk,k} ({{ x}}){\rm d}\Omega ({{ x}})} =
0$
|
(4) |
将式(1)代入式(4),并取规格化位移$\tilde {u}_j$和规格化剪切模量$\tilde {\mu }$为
|
$\left. {\begin{array}{l} \tilde {u}_j = \mu u_j \\ \tilde {\mu } = \ln \mu \\ \end{array}} \right\}$
|
(5) |
使用分部积分和高斯散度定理后,则可以得到计算域的位移积分方程
|
$\eqalign{
& \matrix{
{{{\tilde u}_i}({x^{\rm{p}}}) = \int_\Gamma {{U_{ij}}} ({x^{\rm{p}}},x){t_j}(x){\rm{d}}\Gamma (x) - } \cr
{\int_\Gamma {{T_{ij}}({x^{\rm{p}}},x){{\tilde u}_j}(x){\rm{d}}\Gamma (x)} + } \cr
} \cr
& \int_\Omega {{V_{ij}}({x^{\rm{p}}},x){{\tilde u}_j}(x){\rm{d}}\Omega (x)} \cr} $
|
(6) |
其中,$t_j = \sigma _{ij} n_i $为计算域边界上的面力;$U_{ij}({{ x}}^{\rm p},{{ x}})$和$T_{ij} ({{ x}}^{\rm p},{ {x}}$)分别为开尔文位移基本解和面力基本解[19];另外,域积分中的核函数为
|
$V_{ij} ({{ x}}^{\rm p},{{ x}}) = \frac{-(1-2\nu )}{4\pi \alpha (1-\nu )r^\alpha }[\tilde {\mu }_{,k} r_{,k}(\delta _{ij} + \beta r_{,i} r_{,j} ) + \tilde {\mu }_{,i} r_{,j}-\tilde {\mu }_{,j} r_{,i}]$
|
(7) |
其中,二维问题时{$\beta $} 取2,三维问题时取3,并且{$\alpha $}={$\beta-$}1.
2.2 域积分到边界积分的转化
式(6)位移积分方程的第三项含有域积分,破坏了边界元法只需在边界上离散单元的优势.因此,需要通过径向积分法[27]将其转换成等价的边界积分.
根据径向积分法,位移积分方程中的域积分可以写为
|
$\eqalign{
& \int_\Omega {{V_{ij}}({x^{\rm{p}}},x){{\tilde u}_j}} (x){\rm{d}}\Omega (x) = \cr
& \int_\Gamma {{1 \over {{r^\alpha }({x^{\rm{p}}},y)}}{{\partial r} \over {\partial n}}} F({x^{\rm{p}}},y){\rm{d}}\Gamma (y) \cr} $
|
(8) |
其中
|
$F({{ x}}^{\rm p},{{ y}}) = \int_0^{r({{ x}}^{\rm p},{{ y}})} {V_{ij} ({{ x}}^{\rm p},{{ x}})\tilde {u}_j ({{ x}})r^\alpha {\rm d}r}$
|
(9) |
将式(8)代入式(6),得到只含边界积分的纯边界位移积分方程
|
$\eqalign{
& {{\tilde u}_i}({x^{\rm{p}}}) = \int_\Gamma {{U_{ij}}({x^{\rm{p}}},x){t_j}(x){\rm{d}}\Gamma (x)} - \cr
& \int_\Gamma {{T_{ij}}({x^{\rm{p}}},x){{\tilde u}_j}(x){\rm{d}}\Gamma (x)} + \cr
& \int_\Gamma {{1 \over {{r^\alpha }({x^{\rm{p}}},y)}}{{\partial r} \over {\partial n}}} F({x^{\rm{p}}},y){\rm{d}}\Gamma (y) \cr} $
|
(10) |
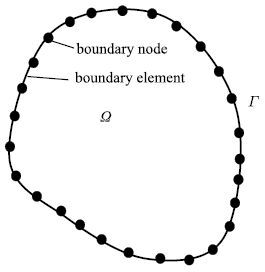
如图 1所示,对计算域$\Omega $的边界进行单元离散,根据形函数[20] $u_i = N_l u_i^l$ 和 $t_i = N_l t_i^l$,将边界上的位移 $u_i $和面力$ t_i$ 用单元节点上的位移${ u}$ 和面力${t}$表示,并在边界单元内进行积分,最终得到关于边界单元节点位移和面力的控制方程
|
${ H}{ u} = { G}{ t}$
|
(11) |
其中,${ H}$和${ G}$为积分得到的系数矩阵.
式(11)是针对弹性力学问题导出的,但对于热传导问题也可以得到类似的公式,因此本文算法既可以用于力学问题,也可以用于热传导问题的求解.
2 集成单元边界元法
2.1 集成单元的形成
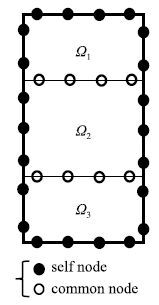
集成单元的概念是单元概念的推广和扩大,即将构成胞元结构的若干个基本胞元组装在一起,构成一个新的结构单元,这个新的结构单元称为集成单元.在多域边界元中,可以将整体结构中的一个或多个计算子域看作一个集成单元,如图 2中的三个计算子域可以看作一个集成单元.首先按照常规多域边界元方法得到各子域的系数矩阵,然后通过子结构消去法[28-29]逐个将多个子域组合在一起,最终得到集成单元的只含外部边界节点的系数矩阵.对于阵列排布等有重复结构的问题,只需针对重复出现的集成单元,组集一次系数矩阵,总体结构可由集成单元组集而成,减少了组集系数矩阵所需的时间,可以显著提高计算效率.
下面以图 2中由三个计算子域构成的集成单元为例介绍集成单元的形成过程.如图 2所示,多域边界元中每个计算域的边界节点都可以分为独立边界节点(self node)和公共边界节点(common node ).这样,对节点顺序进行重排后,任意计算域$\Omega _{i}$的边界元基本方程(式(11))可以写为
|
$H_{\rm ss}^i u_{\rm s}^i + H_{\rm sc}^i u_{\rm c}^i = G_{\rm ss}^i t_{\rm s}^i + G_{\rm sc}^i t_{\rm c}^i$
|
(12) |
|
$H_{\rm cs}^i u_{\rm s}^i + H_{\rm cc}^i u_{\rm c}^i = G_{\rm cs}^i t_{\rm s}^i + G_{\rm cc}^i t_{\rm c}^i$
|
(13) |
式(12)和(13)分别为计算域$\Omega _{i}$中独立边界节点和公共边界节点的基本方程. 其中,$u_{\rm s}^i $,$t_{\rm s}^i $表示独立边界节点的位移和面力,$u_{\rm c}^i$和 $t_{\rm c}^i$表示公共边界节点的位移和面力.
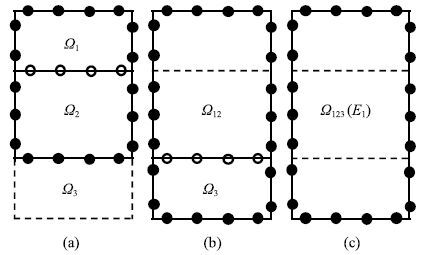
首先考虑计算域$\Omega _{1}$和计算域$\Omega _{2}$之间的组合,此时,计算域$\Omega _{2}$和计算域$\Omega _{3}$之间的公共边界节点变为独立边界节点,如图 3(a)所示.
计算域 $\Omega _{1}$的基本方程为
|
$H_{\rm ss}^1 u_{\rm s}^1 + H_{\rm sc}^1 u_{\rm c}^1 = G_{\rm ss}^1t_{\rm s}^1 + G_{\rm sc}^1 t_{\rm c}^1$
|
(14) |
|
$H_{\rm cs}^1 u_{\rm s}^1 + H_{\rm cc}^1 u_{\rm c}^1 = G_{\rm cs}^1t_{\rm s}^1 + G_{\rm cc}^1 t_{\rm c}^1$
|
(15) |
由式(15)变换可以得到公共边界节点面力$t_{\rm c}^1$的表达式
|
$t_{\rm c}^1 = (G_{\rm cc}^1 )^{-1}(H_{\rm cs}^1 u_{\rm s}^1 +
H_{\rm cc}^1 u_{\rm c}^1-G_{\rm cs}^1 t_{\rm s}^1 )$
|
(16) |
同理可以得到计算域$\Omega _{2}$的基本方程和公共边界节点面力$t_{\rm c}^2 $的表达式
|
$H_{\rm ss}^2 u_{\rm s}^2 + H_{\rm sc}^2 u_{\rm c}^2 = G_{\rm ss}^2t_{\rm s}^2 + G_{\rm sc}^2 t_{\rm c}^2~~~~~~~~~$
|
(17) |
|
$H_{\rm cs}^2 u_{\rm s}^2 + H_{\rm cc}^2 u_{\rm c}^2 = G_{\rm cs}^2t_{\rm s}^2 + G_{\rm cc}^2 t_{\rm c}^2~~~~~~~~~$
|
(18) |
|
$t_{\rm c}^2 = (G_{\rm cc}^2 )^{-2}(H_{\rm cs}^2 u_{\rm s}^2 +
H_{\rm cc}^2 u_{\rm c}^2-G_{\rm cs}^2 t_{\rm s}^2 )$
|
(19) |
计算域$\Omega _{1}$和计算域$\Omega _{2}$的公共边界满足界面协调条件,即
|
$u_{\rm c}^1 = u_{\rm c}^2 = u_{\rm c}$
|
(20) |
|
$t_{\rm c}^1 + t_{\rm c}^2 = 0$
|
(21) |
将式(16)、(19)、(20)代入式(21),并进行化简,得到公共边界节点位移 $u_{\rm c}$ 的表达式
|
$u_{\rm c} = U_1 u_{\rm s}^1 + U_2 t_{\rm s}^1 + U_3 u_{\rm s}^2 +
U_4 t_{\rm s}^2$
|
(22) |
其中,$U_1 $,$U_2 $,$U_3 $和$U_4 $的表达式分别为
|
$\begin{array}{lll} U_1 =-[(G_{\rm cc}^1 )^{-1}H_{\rm cc}^1 + (G_{\rm cc}^2 )^{-1}H_{\rm cc}^2]^{-1}(G_{\rm cc}^1 )^{-1}H_{\rm cs}^1 \\ U_2 = [(G_{\rm cc}^1 )^{-1}H_{\rm cc}^1 + (G_{\rm cc}^2 )^{-1}H_{\rm cc}^2]^{-1}(G_{\rm cc}^1 )^{-1}G_{\rm cs}^1 \\ U_3 =-[(G_{\rm cc}^1 )^{-1}H_{\rm cc}^1 + (G_{\rm cc}^2 )^{-1}H_{\rm cc}^2]^{-1}(G_{\rm cc}^1 )^{-1}H_{\rm cs}^2 \\ U_4 = [(G_{\rm cc}^1 )^{-1}H_{\rm cc}^1 + (G_{\rm cc}^2 )^{-1}H_{\rm cc}^2]^{-1}(G_{\rm cc}^1 )^{-1}G_{\rm cs}^2 \end{array}$
|
将式(22)代入式(16),得到计算域$\Omega _{1}$和计算域$\Omega _{2}$的公共边界节点面力
|
$t_{\rm c}^1 = T_1 u_{\rm s}^1 + T_2 t_{\rm s}^1 + T_3 u_{\rm s}^2+ T_4 t_{\rm s}^2$
|
(23) |
其中,$T_1 $,$T_2$,$T_3$和 $T_4$的表达式为
|
$\begin{array}{l} T_1 = (G_{\rm cc}^1 )^{-1}(H_{\rm cc}^1 U_1 + H_{\rm cs}^1 ) \\ T_2 = (G_{\rm cc}^1 )^{-1}(H_{\rm cc}^1 U_2-G_{\rm cs}^1 ) \\ T_3 = (G_{\rm cc}^1 )^{-1}H_{\rm cc}^1 U_3 \\ T_4 = (G_{\rm cc}^1 )^{-1}H_{\rm cc}^1 U_4 \\ \end{array}$
|
将式(21)、(22)、(23)代入式(14)、(17),化简后得到计算域$\Omega _{1}$和计算域$\Omega _{2}$独立边界点的控制方程
|
${ H}_{12} { u}_{12} = { G}_{12} { t}_{12}$
|
(24) |
其中,系数矩阵
|
$\eqalign{
& {H_{12}} = \left[ {\matrix{
{H_{{\rm{ss}}}^1 + H_{{\rm{sc}}}^1{U_1} - G_{{\rm{sc}}}^1{T_1}} & {H_{{\rm{sc}}}^1{U_3} - G_{{\rm{sc}}}^1{T_3}} \cr
{H_{{\rm{sc}}}^2{U_1} + G_{{\rm{sc}}}^2{T_1}} & {H_{{\rm{ss}}}^2 + H_{{\rm{sc}}}^2{U_3} + G_{{\rm{sc}}}^2{T_3}} \cr
} } \right] \cr
& {G_{12}} = \left[ {\matrix{
{G_{{\rm{ss}}}^1 - H_{{\rm{sc}}}^1{U_2} + G_{{\rm{sc}}}^1{T_2}} & { - H_{{\rm{sc}}}^1{U_4} + G_{{\rm{sc}}}^1{T_4}} \cr
{ - H_{{\rm{sc}}}^2{U_2} - G_{{\rm{sc}}}^2{T_2}} & {G_{{\rm{ss}}}^2 - H_{{\rm{sc}}}^2{U_4} - G_{{\rm{sc}}}^2{T_4}} \cr
} } \right] \cr} $
|
位移、面力向量为
|
${ u}_{12} = \left[{{\begin{array}{*{20}c} {u_{\rm s}^1 } \\ {u_{\rm s}^2 } \\\end{array} }} \right],\quad { t}_{12} = \left[{{\begin{array}{*{20}c} {t_{\rm s}^1 } \\ {t_{\rm s}^2 } \\\end{array} }} \right]
$
|
下面考虑计算域$\Omega _{12}$ 和计算域$\Omega _{3}$的组合,此时,计算域$\Omega _{2}$和计算域 $\Omega _{3}$之间的边界节点变为公共边界节点,如图 3(b)所示.经过节点重新排序,计算域$\Omega _{12}$的基本方程(式(24))同样可以写成独立边界节点和公共边界节点的形式
|
$H_{\rm ss}^{12} u_{\rm s}^{12} + H_{\rm sc}^{12} u_{\rm c}^{12} =
G_{\rm ss}^{12} t_{\rm s}^{12} + G_{\rm sc}^{12} t_{\rm c}^{12}$
|
(25) |
|
$H_{\rm cs}^{12} u_{\rm s}^{12} + H_{\rm cc}^{12} u_{\rm c}^{12} =
G_{\rm cs}^{12} t_{\rm s}^{12} + G_{\rm cc}^{12} t_{\rm c}^{12}$
|
(26) |
按照式(22)$\sim$式(24)的操作过程,消去计算域$\Omega _{12}$和计算域 $\Omega _{3}$间的公共边界,可得到计算域$\Omega _{123}$边界节点的基本方程,即集成单元$E_{1}$ 的基本方程
|
${ H}_{{\rm E}1} { u}_{{\rm E}1} = { G}_{{\rm E}1} {t}_{{\rm E}1}$
|
(27) |
2.2 集成单元的组集
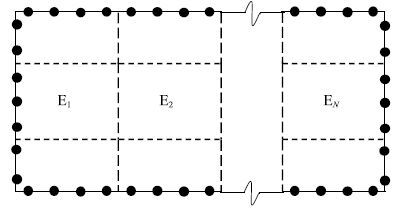
集成单元的概念是普通有限元法、边界元法中单元概念的推广,在得到集成单元的基本方程(式(27))后,可以像普通有限单元法、边界元法那样用集成单元来组集重复出现的复杂结构.因此,集成单元既可以作为独立结构进行热、力学分析,也可以由多个集成单元按照2.1节所述方法继续组集,形成总体结构计算公式,如图 4所示.
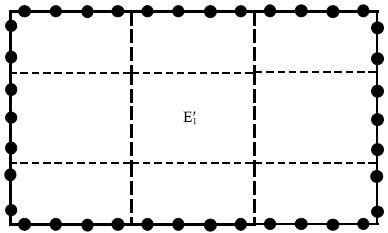
对于阵列排布的结构,由于只需针对重复出现的集成单元形成一次系数矩阵,避免了边界元法必须遍及计算域内所有节点积分的缺点,计算效率显著提高.且对于更为复杂的问题,集成单元可以继续组集成更高级的集成单元,如图 5所示,组集效率可以显著提高.
2.3 集成单元的旋转
对于图 6所示的带弧度的结构,总体结构可能需要通过集成单元旋转一定角度组集而成.
考虑图 6所示的二维问题,集成单元整体顺时针旋转$\alpha $角.任意节点旋转前后的坐标关系为[30-31]
|
${{ {X}'}} = {{ Q}} \cdot {{ X}}$
|
(28) |
其中,${{ X}}$为旋转前的节点坐标,$ {{{X}'}}$为旋转后的节点坐标,节点坐标旋转矩阵为
|
${{ Q}} = \left[{{\begin{array}{*{20}c} {\cos \alpha } & {\sin \alpha } & 0 \\ {-\sin \alpha } & {\cos \alpha } & 0 \\ 0 & 0 & 1 \\\end{array} }} \right]$
|
(29) |
旋转后集成单元的位移可表示为
|
${{ {U}'}} = {{ Q}}_{\rm r} \cdot {{ U}}$
|
(30) |
其中,${{ U}}$,${{{U}'}}$为旋转前、后集成单元边界上的位移,位移旋转矩阵为
|
${{ Q}}_{\rm r} = \left[{{\begin{array}{*{20}c} {{ Q}} & {{ 0}} & \ldots & {{ 0}} \\ {{ 0}} & {{ Q}} & \cdots & {{ 0}} \\ \vdots & \vdots & \ddots & \vdots \\ {{ 0}} & {{ 0}} & \cdots & {{ Q}} \\\end{array} }} \right]$
|
则旋转前位移可表示为
|
${{ U}} = {{ Q}}_{\rm r}^{-1} \cdot {{ {U}'}}$
|
(31) |
同理,可得旋转前集成单元边界上的面力表达式
|
${{ T}} = {{Q}}_{\rm r}^{-1} \cdot {{ {T}'}}$
|
(32) |
将式(31)、(32)代入集成单元基本方程式(27),得到
|
${{ {H}'}} \cdot {{ {U}'}} = {{ {G}'}} \cdot {{{T}'}}$
|
(33) |
其中,${{ {H}'}}$和${{ {G}'}}$分别为旋转后集成单元的系数矩阵
|
${{ {H}'}} = {{ H}} \cdot {{ Q}}^{-{{1}}}_{\rm r} $
|
(34) |
|
${{ {G}'}} = {{ G}} \cdot {{ Q}}_{\rm r}^{-{{1}}}$
|
(35) |
这样,对于需要旋转的集成单元,只需在旋转前的系数矩阵上右乘旋转矩阵${Q}_{\rm r}$ 的逆矩阵,之后按2.1节介绍的方法进行组集即可.
3 算例
3.1 矩形功能梯度平板
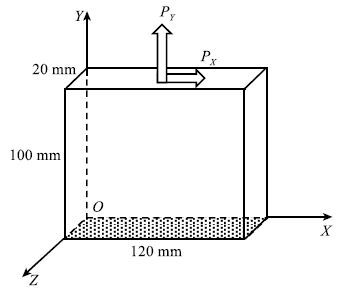
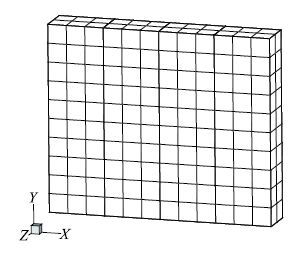
算例一用图 7所示的矩形功能梯度平板对本文算法进行验证,并对计算效率进行分析.矩形功能梯度平板的尺寸如图 7所示,弹性模量$E$沿$Y$方向线性变化,表达式为$E=0.5y+130.0$GPa,泊松比为常数$\nu =0.3$.平板下表面固定,上表面分别受$X$方向和$Y$方向的均布力:$P_{X
}=$100.0 MPa,$P_Y = $ 1 000.0 MPa,其它表面受力为零.
为了对本文算法进行验证,分别采用单域边界元法(berim_1)、多域边界元法(berim_4)和本文提出的集成单元边界元法(present)对功能梯度平板进行分析.三种算法采用相同尺寸的网格,单域边界元法所用网格如图 8所示,多域边界元将模型沿$X$方向均分为四个计算域.集成单元边界元法取模型的1/4作为一个集成单元,只需针对该1/4结构建立模型和剖分网格.
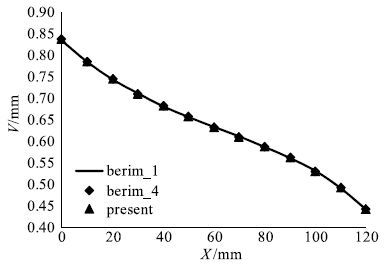
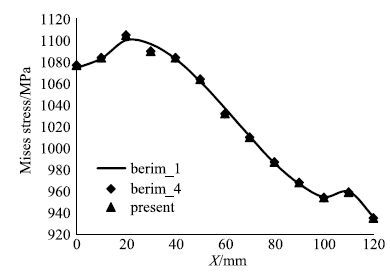
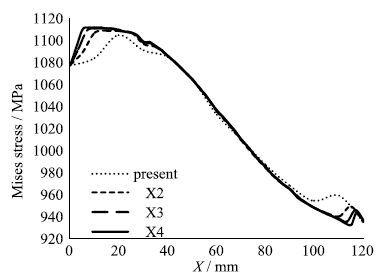
图 9和10分别给出了三种算法计算得到的上表面$z=10$mm中线上$Y$方向位移$V$和米塞斯应力的比较情况.可以看出,本文提出的集成单元边界元法计算结果与单域边界元算法和多域边界元算法符合很好,满足工程问题的精度需要.本文给出的网格已经能够得到精度较高的位移结果,为了进一步考察网格对应力精度的影响,分别对网格加密2$\sim$4倍来比较应力计算结果.图 11给出了四种网格计算得到的上表面$z=10$mm中线上米塞斯应力的比较情况.可以看出,本文给出的粗糙网格得到的米塞斯应力在两端存在较大误差,当网格加密后,应力结果趋于稳定.
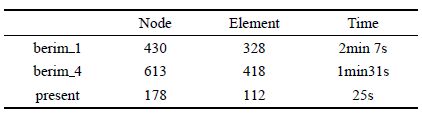
表 1给出了三种算法的边界节点数、边界单元数和计算时间的比较情况.由于单域边界元法需要遍及域内所有边界点积分,所以耗时最长(2 min 7 s).多域边界元法虽然使用的边界节点和边界单元更多,但由于其只需在4个计算域内单独积分,计算耗时少于单域边界元法(1min 31 s).本文算法只需针对集成单元积分一次,计算效率较前两种方法显著提高(25s).
表 1(Table 1)

表 1 计算效率比较
Table 1 Comparison of computational effciency
|
表 1 计算效率比较
Table 1 Comparison of computational effciency
|
3.2 含冷却通道的圆筒结构
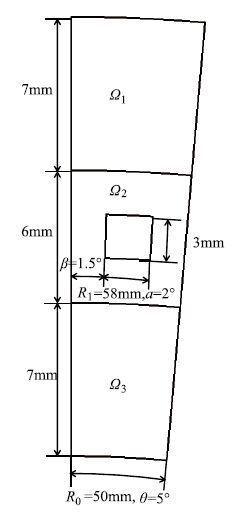
算例二对图 12所示的含冷却通道的圆筒结构进行分析.整个圆筒分为三层,其中中间一层包含方形冷却通道. 圆筒内壁半径为50mm,从里到外三层结构厚度分别为7 mm,6 mm和7 mm,$Z$方向厚度均为20mm. 包含冷却通道的胞元结构夹角$\theta =5^\circ$,冷却通道具体尺寸见图 13所示.内、外两层为均质材料,材料参数为:导热系数$\lambda _{\rm in}$= 10.0 W/(m$ \cdot$K),$\lambda_{\rm out}$=16.0W/(m$ \cdot $K) ;弹性模量$E_{\rm in}$= 140.0GPa,$E_{\rm out}$=200.0 GPa.中间一层是导热系数和弹性模量沿径向变化的功能梯度材料,表达式为$\lambda _{\rm mid}=R-47.0$ W/(m$ \cdot$K),$E_{\rm mid}$=10.0$R-$430.0GPa,$R$为圆筒结构半径. 整个圆筒的泊松比为常数$\nu =0.3$.
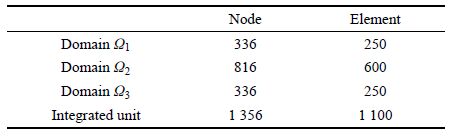
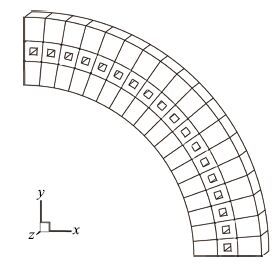
首先按照几何对称面取出含一个通道的胞元结构作为集成单元,将集成单元划分为三个边界元计算域,如图 13和14所示.表 2给出了三个计算域的边界节点数和边界单元数.形成集成单元的系数矩阵后,通过旋转组集,可以快速集成如图 12所示的四分之一圆筒结构分析模型.圆筒内、外壁面温度分别取1 000 K和300 K,其他壁面绝热.$x=0$面固定,$y=0$面受$X$向的均布拉力$F_{X}=1.0$ MPa,其它面自由.
表 2(Table 2)

表 2 集成单元信息
Table 2 Numbers of mesh and node
|
表 2 集成单元信息
Table 2 Numbers of mesh and node
|
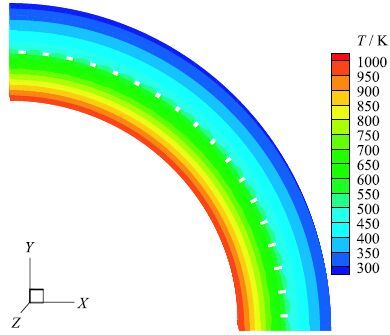
图 15和16给出了由18个集成单元组成的四分之一圆筒结构的温度和$X$方向位移分布云图.由于结构和温度边界条件的轴对称性,采用多域边界元法(berim)计算一个集成单元结构的温度分布来验证本文算法.图 17给出了两种算法计算的 $z=20$ mm面上$x=3$mm处截线的温度值比较情况.可以看出,本文提出的集成单元结果与berim结果符合得很好.
3.3 超燃冲压发动机燃烧室热分析
算例三对图 18所示的超燃冲压发动机燃烧室凹腔进行分析.取含一根冷却通道的胞元结构建立边界元计算模型,并将其定义为一个集成单元.整个结构由9个集成单元组成,每个厚度为5 mm,截面尺寸如图 19所示.如图 20和图 21所示,每个集成单元的外壁面离散成1 326个边界节点和1022个四节点边界单元;内部冷却通道壁面离散成552个边界节点和560个边界单元.
燃烧室材料导热系数$\lambda =11.30 ~{\rm W/(m \cdot K)}$,上表面指定温度$T_{\rm up}$=500K,下表面隔离段给定温度$T_{\rm low1}$=1 000K,燃烧室段指定温度$T_{\rm low2}$=2 000K,冷却通道壁面给定热流密度$q=-1.2$MW/m$^{2}$,其他表面热流密度为零.
图 22给出了整体结构的温度分布云图,图 23给出了冷却管道热流密度分别为$q=$$-1.2$ MW/m$^{2}$(cooling)和$q=0$(no cooling)时,燃烧室过冷却通道中心截面$z=30$mm处AB线(如图 19所示)上的温度分布.从图中可以看出,冷却通道明显降低了燃烧室壁面的温度,起到了比较明显的冷却效果.
4 结论
本文提出了基于子结构法思想的集成单元边界元法,可对主动冷却系统等周期性结构进行快速分析.本文算法只需针对重复出现的胞元结构建立边界元模型,建模方便;系数矩阵只需计算一次,且最终系数矩阵只含结构外部边界节点变量,计算规模大幅减小,计算效率显著提高.
参考文献
| [1] |
黄伟, 罗世彬, 王振国. 临近空间高超声速飞行器关键技术及展望[J].
宇航学报,2010, 31 (5) : 1259-1265.
( Huang Wei, Luo Shibin, Wang Zhen guo. Key techniques and prospect of near-space hypersonic vehicle[J].
Journal of Astronautics,2010, 31 (5) : 1259-1265.
(in Chinese) ) ( 0) 0)
|
| [2] |
王振国, 梁剑寒, 丁猛, 等. 高超声速飞行器动力系统研究进展[J].
力学进展,2009, 39 (6) : 716-739.
( Wang Zhenguo, Liang Jianhan, Ding Meng, et al. A review on hypersonic air-breathing propulsion system[J].
Advances in Mechanics,2009, 39 (6) : 716-739.
(in Chinese) ) ( 0) 0)
|
| [3] |
刘兴洲. 中国超燃冲压发动机研究回顾[J].
推进技术,2008, 29 (4) : 385-395.
( Liu Xingzhou. Review of scramjet research in China[J].
Journal of Propulsion Technology,2008, 29 (4) : 385-395.
(in Chinese) ) ( 0) 0)
|
| [4] |
韩洪涛, 王友利. 2013 年国外高超声速技术发展回顾[J].
中国航天,2014, 03 : 16-20.
( Han Hongtao, Wang Youli. Review of overseas hypersonic technology development in 2013[J].
Aerospace China,2014, 03 : 16-20.
(in Chinese) ) ( 0) 0)
|
| [5] |
牛文, 李文杰, 胡冬冬, 等. 2014 年国外高超声速技术发展动态回顾[J].
飞航导弹,2015, 01 : 27-34.
( Niu Wen, Li Wenjie, Hu Dongdong, et al. Review of overseas hypersonic technology development in 2014[J].
Aerodynamic Missile Journal,2015, 01 : 27-34.
(in Chinese) ) ( 0) 0)
|
| [6] |
贺武生. 超燃冲压发动机研究综述[J].
火箭推进,2005, 31 (1) : 29-32.
( He Wusheng. Review of scramjet engine development[J].
Journal of Rocket Propulsion,2005, 31 (1) : 29-32.
(in Chinese) ) ( 0) 0)
|
| [7] |
Thermal-structural design study of an airframe-integrated scramjet finial report. NASA CR 159039,1980
( 0) 0)
|
| [8] |
肖红雨, 高峰, 李宁. 再生冷却技术在超燃冲压发动机中的应用与发展[J].
飞航导弹,2013, 8 (8) : 78-81.
( Xiao Hongyu, Gao feng, Li Ning. Application and development of regenerative cooling technology in scramjet[J].
Aerodynamic Missile Journal,2013, 8 (8) : 78-81.
(in Chinese) ) ( 0) 0)
|
| [9] |
任加万, 谭永华. 冲压发动机燃烧室热防护技术[J].
火箭推进,2006, 32 (4) : 38-42.
( Ren Jiawan, Tan Yonghua. Thermal protection techniques of ramjet combustor[J].
Journal of Rocket Propulsion,2006, 32 (4) : 38-42.
(in Chinese) ) ( 0) 0)
|
| [10] |
刘世俭, 刘兴洲. 超燃冲压发动机可贮存碳氢燃料再生主动冷却换热过程分析[J].
飞航导弹,2009, 3 (3) : 48-52.
( Liu Shijian, Liu Xingzhou. Analysis of scramjet hydrocarbon fuel storage regeneration active cooling heat transfer process[J].
Aerodynamic Missile Journal,2009, 3 (3) : 48-52.
(in Chinese) ) ( 0) 0)
|
| [11] |
仲峰泉, 范学军, 俞刚. 带主动冷却的超声速燃烧室传热分析[J].
推进技术,2009, 30 (5) : 513-517.
( Zhong Fengquan, Fan Xuejun, Yu Gang. Heat transfer analysis for actively cooled supersonic combustor[J].
Journal of Propulsion Technology,2009, 30 (5) : 513-517.
(in Chinese) ) ( 0) 0)
|
| [12] |
王勖成.
有限单元法[M]. 北京: 清华大学出版社, 2003 .
( Wang Xucheng.
Finite Element Method[M]. Beijing: Tsinghua University Press, 2003 .
(in Chinese) ) ( 0) 0)
|
| [13] |
Zienkiewicz OC, Taylor RL.
The Finite Element Method. Butterworth-Heinemann[M]. 2000 .
( 0) 0)
|
| [14] |
Liu GR, Quek SS. The Finite Element Method: A Practical Course. Elsevier, 2013
( 0) 0)
|
| [15] |
Richtmyer RD, Morton KW. Difference Methods for Initial-Value Problems, New York, Banerjee PK, 1967
( 0) 0)
|
| [16] |
Mitchell AR, Griffiths DF. The finite difference method in partial differential equations//Mitchell AR, Griffiths DF[J].
AWiley-Interscience Publication,1980, 43 (1) : S76-S78.
( 0) 0)
|
| [17] |
Becker AA. The Boundary Element Method in Engineering. London: McGraw –Hill Book Co.,1992
( 0) 0)
|
| [18] |
Brebbia CA, Dominguez J. Boundary Elements: An Introductory Course. Southampton and Boston: Comput. Mech. Publicatons and Mc Graw-Hill Book Co.,1992
( 0) 0)
|
| [19] |
Beer G, Smith I, Duenser C.
The Boundary Element Method with Programming[M]. Wien: Springer-Verlag, 2008 .
( 0) 0)
|
| [20] |
Gao XW, Davies TG.
Boundary Element Programming in Mechanics. Cambridge, Cambridge University Press[M]. 2002 .
( 0) 0)
|
| [21] |
Tanaka M, Sladek V, Sladek J. Regularization techniques applied to boundary element methods[J].
Appl. Mech. Rev,1994, 47 : 457-499.
DOI: 10.1115/1.3111062. ( 0) 0)
|
| [22] |
Beer G. Programming the Boundary Element Method. An Introduction for Engineers. Chichester, John Wiley & Sons, Ltd, 2001
( 0) 0)
|
| [23] |
Gao X W, Guo L, Zhang C. Three-step multi-domain BEM solver for nonhomogeneous material problems[J].
Engineering Analysis with Boundary Elements,2007, 31 (12) : 965-973.
DOI: 10.1016/j.enganabound.2007.06.002. ( 0) 0)
|
| [24] |
王永岩.
动态子结构方法理论及应用. 科学出版社[M]. 1999 .
( Wang Yongyan.
Theory and Application of Dynamic Substructure Method. Science Press[M]. 1999 .
(in Chinese) ) ( 0) 0)
|
| [25] |
Liu J, Peng HF, Gao XW, et al. A traction-recovery method for evaluating boundary stresses on thermal elasticity problems of FGMs[J].
Engineering Analysis with Boundary Elements,2015, 61 : 226-231.
DOI: 10.1016/j.enganabound.2015.07.016. ( 0) 0)
|
| [26] |
高效伟, 杨恺. 功能梯度材料结构的热应力边界元分析[J].
力学学报,2011, 43 (1) : 136-143.
( Gao Xiaowei, Yang Kai. Thermal stress analysis of functionally graded material structures using boundary element method[J].
Chinese Journal of Theoretical and Applied Mechnics,2011, 43 (1) : 136-143.
(in Chinese) ) ( 0) 0)
|
| [27] |
Gao XW. The radial integration method for evaluation of domain integrals with boundary-only discretization[J].
Engineering Analysis with Boundary Elements,2002, 26 : 905-916.
DOI: 10.1016/S0955-7997(02)00039-5. ( 0) 0)
|
| [28] |
Przemieniecki JS. Theory of Matrix Structural Analysis. New York: Dover Publications, 2001
( 0) 0)
|
| [29] |
王刚, 齐朝晖, 汪菁. 含铰接杆系结构几何非线性分析子结构方法[J].
力学学报,2014, 46 (2) : 273-283.
( Wang Gang, Qi Zhaohui, Wang Jing. Substructure methods of geometric nonlinear analysis for member structures with hinged supports[J].
Chinese Journal of Theoretical and Applied Mechnics,2014, 46 (2) : 273-283.
(in Chinese) ) ( 0) 0)
|
| [30] |
黄筑平.
连续介质力学基础[M]. 北京: 高等教育出版社, 2004 .
( Huang Zhuping.
The Basis of Continuum Mechanics[M]. Beijing: Higher Education Press, 2004 .
(in Chinese) ) ( 0) 0)
|
| [31] |
黄克智, 薛明德, 陆明万.
张量分析. 清华大学出版社[M]. 2003 .
( Huang Kezhi, Xue Mingde, Lu Mingwan.
Tensor Analysis. Tsinghua University Press[M]. 2003 .
(in Chinese) ) ( 0) 0)
|
INTEGRATED UNIT BEM AND ITS APPLICATION IN ANALYSIS OF ACTIVELY COOLING TPS
Gao Xiaowei

,
Liu Jian,
Peng Haifeng
State Key Laboratory of Structural Analysis for Industrial Equipment, School of Aeronautics and Astronautics, Dalian University of Technology, Dalian 116024, China
Abstract:
With the fast development of hypersonic aircrafts, the traditional passive thermal protection system (TPS) can't a ord the increasing demand of the thermal protection for aircrafts and engines. As a result, the actively cooling TPS has received more and more attentions. The commonly used technologies do require a substantially much more time due to the complexity of the structures. In this paper, the integrated unit method is proposed for solving spatially periodical structural problems using the boundary element method (BEM) and it is used to solve the thermal and mechanical problems appearing in the TPS with actively cooling channels. In this method, the BEM cell equation only needs to be established for one computational cell and the integrated unit can be formed by a specified number of cell equations. The equations of final system can be formed by the integrated unit equations. The proposed integrated unit method inherits the variableelimination idea of the sub-structure technique and assimilates the easy assembling characteristic of the conventional finite and boundary elements, and therefore is suitable for fast analysis of large-scale spatially periodical structural problems. As the coefficient matrices of the integrated unit only needs to be established once and the equations of final system only includes boundary nodal variables, the computational efficiency can be improved considerably. Three numerical examples for actively cooling combustors of scramjet engine are given to demonstrate the computational accuracy and efficiency of the proposed method.
Key words: integrated unit boundary element method fast computational algorithm actively cooling channels










 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 2016, Vol. 48
2016, Vol. 48