引言

二次大战期间，大量的美国自由轮出现严重的断裂事故. 战后的事故分析研究促使一门崭新的固体力学分支"断裂力学"的诞生. 据此发展出重大结构防断裂设计的理论，并产生了巨大的安全效益和经济效益.

断裂力学并不是一般所谓的"断裂"的力学. 一般的断裂现象，如一根试棒的拉伸断裂，试棒的拉伸断裂的判据是拉应力达到材料的强度极限，早已为人们所熟知. 对于钢试棒，其断裂总是发生在显著的塑性变形之后. 然而自由轮的钢板船身的断裂却发生在舱口角点处出现裂纹之后，呈脆性的断裂. 所以，断裂力学的任务是要找到含裂纹的韧性构件在载荷作用下，裂纹发生扩展而导致脆性断裂的规律和条件.

断裂力学在实际问题中的研究对象是含疲劳裂纹的韧性构件，在弹性理论里被看作是带理想裂纹的弹性连续介质，得到的弹性理论严格解(rigorous solution)里有应力奇异性的项，使得裂纹端点处应力为无限大. 在以往的固体力学里没有处理应力奇异性的办法.应力奇异性迫使断裂力学放弃应力分量的判据，改用应力强度因子的判据，形成了整套断裂力学的新概念.事实上，断裂力学从开始研究到概念的形成有一个发展的过程，要在断裂力学中不用应力作为判据的力学参量，换成应力强度因子和断裂韧性的判据，如果没有足够的实践证据的支持是难以令人接受的.1955年的deHavilland Comet喷气式飞机，1955---1956年的3个新发电机组的重型转子，以及1957年的北极星和民兵火箭燃烧室，接连了发生重大事故.这些事故的事后分析结果，证明Irwin的应力强度因子脆性断裂判据是可靠的，因而断裂力学得到了国际工程界的认可^[1].断裂力学的历史不长，却包含了丰富的研究和实践经验.

尽管今天的断裂力学^[2-3]在理论、概念、实验、应用等各个方面都已趋于成熟，但研究仍在继续.

本文对断裂力学的判据作了扼要的综述，从Inglis 和 Griffith 的著名论文到Irwin和Rice等的奠基性贡献. 在综述中归纳出断裂力学判据中目前还没有较好解决的几个问题. 在总结以往断裂力学研究经验的基础上，探讨了对判据作进一步研究的可能切入点，并对裂纹端应力奇异性的来源及裂纹端应力强度因子的物理意义进行了讨论.

Rossmanith^[1]以丰富的文献和史料记述了断裂力学发展的全过程. 他在结语中说道："格言云：经验是最好的教师，而经验来自毕生的学习过程. 反映一个主题的发展中的新发现有根在以前的经验中，它将揭开一个又一个的真理并带来正确的展望". 把这句话应用到本文就是：断裂力学的下一个发展要在断裂力学的上一个发展期所取得的经验中借鉴. 前人只能从断裂力学的一个问题到下一个问题逐个进行研究，而当下断裂力学的研究的一个特点是我们可以把断裂力学的全部遗留问题综合起来研究，用前人在逐个问题的研究经验中所累积的智慧集成，来对综合起来的断裂力学问题进行研究.

本文第1节是与断裂力学有关的弹性理论平面问题的内容的介绍，第2节是对断裂力学起步阶段的探索过程的回顾，第3节为线弹性断裂力学的建立及拓展过程的描述，第4节为${{K}_{\text{IC}}},{{J}_{\text{IC}}}$测试的标准化的介绍，第5节是关于断裂力学的判据原理的讨论，第6节是在断裂力学判据研究中归纳出目前还没有得到较好解决的几个问题，第7节是关于Sinclair的应力奇异性的研究的介绍，第8节是关于双材料角界面端应力奇异性的介绍，第9节是关于裂纹端应力奇异性的源及裂纹端应力强度因子的物理意义的讨论，第10节为总结与展望.

1 弹性理论提供的理论基础 1.1 Inglis椭圆孔应力集中

Kirsch^[4]于1898年，用平面问题极坐标通解，得到了带圆孔的无限平板受拉伸的解析解，圆孔的应力集中系数等于3.继第一个应力集中问题之后，1913年，Inglis^[5] 用椭圆坐标系解带椭圆孔的无限平板受拉应力σ的平面问题.由得到的解析解知，最大应力发生在长轴的端点，应力集中系数公式是

${{\sigma }_{\max }}=(1+2\frac{a}{b})\sigma$

(1)

式中，2a和 2b 分别是椭圆的长轴和短轴. Inglis扩展了对应力集中的了解. 由式(1)可知：a/b=1 000时，应力集中系数k=2 001,当a/b=2 000时,k=4 001,当b → 0时，$k\to \infty $. Inglis 把裂纹看作是b趋于0的椭圆孔，并由此得出裂纹端部应力集中为无限大，首次把裂纹作为短轴为零的椭圆孔而引入到应力分析中.

1.2 Westergaard裂纹端应力场复变函数解

1939年，Westergaard^[6] 用应力函数法解带理想裂纹(裂纹长度为2a)的无限大平板受到拉伸的问题.坐标原点在裂纹的中点. 他取一个复变数$z=x+{\rm i}y$的复变解析函数$Z_{\rm I}(z)$. 并以 $Z_{\rm I}(z)$的一次积分$\tilde Z_{\rm I}(z)$的虚部和二次积分$\tilde{\tilde{Z}}_{\rm I}(z)$的实部组成Airy应力函数$U={\rm Re} \tilde{\tilde{Z}}_{\rm I}(z)+y {\rm Im} \tilde{Z}_{\rm I}(z)$令

${Z}_{\rm I}(z)=\dfrac{\sigma z}{\sqrt{z^2-a^2}}$

(2)

这个应力函数U是重调和函数，正好满足无限远和理想裂纹的全部边界条件. 得到了在裂纹之外的裂纹所在面上的拉应力为

${{\sigma }_{y}}=\frac{\sigma }{\sqrt{1-{{a}^{2}}/{{x}^{2}}}}$

(3)

Westergaard解的意义在于它不同于Inglis解，它是第一个直接按理想裂纹的边界条件而求得的弹性理论解，它对断裂力学的诞生起到了关键的作用. 这里，理想裂纹定义为二个自由的裂纹平面重合的裂纹.

1.3 Williams裂纹端奇异性应力场的模式

1957年，Williams^[7] 用分离变量法求带半无限长裂纹的无限大平板不受载荷作用的齐次问题，采用极坐标，坐标原点放在裂纹的端点. 应力函数取如下的级数形式

$U(r,\theta ,\lambda )=\sum\limits_{\lambda =-\infty }^{\infty }{{{r}^{\lambda +1}}}{{F}_{\lambda }}(\theta )$

(4)

$\begin{align} & {{F}_{\lambda }}\left( \theta \right)={{A}_{\lambda }}\cos [\left( \lambda +1 \right)\theta ]+{{B}_{\lambda }}\sin [\left( \lambda +1 \right)\theta ]+ \\ & {{C}_{\lambda }}\cos [\left( \lambda -1 \right)\theta ]+{{D}_{\lambda }}\sin [\left( \lambda -1 \right)\theta ] \\ \end{align}$

(5)

λ为特征值，理想裂纹处的边界条件为

${{\sigma }_{\theta }}={{\tau }_{r\theta }}=0(\theta =\pm \pi )$

(6)

极坐标原点放在裂纹尖端. 按照边界条件，待定系数$A_\lambda,B_\lambda,C_\lambda,D_\lambda$有非零解的条件是

$\sin (2\lambda \pi)=0 $

(7)

故有，特征值$\lambda =n/2(n=0,1,2,\cdots )$.

由此得到在对称载荷下，取 $\lambda =1/2$，Ⅰ型裂纹端附近的对称应力场的应力分量的渐近式 (r→0) 为

$\left. \begin{align} & {{\sigma }_{x}}=\frac{{{K}_{\text{I}}}}{\sqrt{2\pi }}{{r}^{\lambda -1}}\cos \frac{\theta }{2}(1-\sin \frac{\theta }{2}\sin \frac{3\theta }{2}) \\ & {{\sigma }_{y}}=\frac{{{K}_{\text{I}}}}{\sqrt{2\pi }}{{r}^{\lambda -1}}\cos \frac{\theta }{2}(1+\sin \frac{\theta }{2}\sin \frac{3\theta }{2}) \\ & {{\sigma }_{xy}}=\frac{{{K}_{\text{I}}}}{\sqrt{2\pi }}{{r}^{\lambda -1}}\sin \frac{\theta }{2}\cos \frac{\theta }{2}\cos \frac{3\theta }{2} \\ \end{align} \right\}$

(8)

在反对称载荷下，取$\lambda =n/2(n=0,1,2,\cdots )$,Ⅱ型裂纹端附近的反对称应力场的应力分量的渐近式 (r→0) 为

$\left. \begin{align} & {{\sigma }_{x}}=\frac{{{K}_{II}}}{\sqrt{2\pi }}{{r}^{\lambda -1}}\sin \frac{\theta }{2}(1+\cos \frac{\theta }{2}\sin \frac{3\theta }{2}) \\ & {{\sigma }_{y}}=\frac{{{K}_{II}}}{\sqrt{2\pi }}{{r}^{\lambda -1}}\sin \frac{\theta }{2}\cos \frac{\theta }{2}\cos \frac{3\theta }{2} \\ & {{\sigma }_{xy}}=\frac{{{K}_{II}}}{\sqrt{2\pi }}{{r}^{\lambda -1}}\cos \frac{\theta }{2}(1-\sin \frac{\theta }{2}\sin \frac{3\theta }{2}) \\ \end{align} \right\}$

(9)

式(8)和式(9)十分清晰地描绘出Ⅰ型和 Ⅱ型裂纹端邻近四周的应力分布的情况.Williams的这个结果揭示裂纹端附近应力分布有一个特殊规律：即应力与r的平方根成反比，式中，$\lambda-1=-1/2$称为奇异性指数，当$ r \to 0 $,应力趋于无限大. 公式中与θ有关的角分布函数具有恒定不变的形式，即与平板的形状及载荷的分布无关. 此外，裂纹端附近邻域内的各应力分量$\sigma_{ij}(r,\theta)$的数值仅依赖于一个常数 $K_{\rm I}$或$K_{\rm II}$.

在面外剪切载荷下，取$\lambda =n/2(n=0,1,2,\cdots )$，Ⅲ型裂纹端的反对称应力场的应力分量的渐近式 (r→0)为

$\left. \begin{align} & {{\tau }_{xz}}=\frac{{{K}_{\text{Ⅲ}}}}{\sqrt{2\pi }}{{r}^{\lambda -1}}\sin \frac{\theta }{2} \\ & {{\tau }_{yz}}=\frac{{{K}_{\text{Ⅲ}}}}{\sqrt{2\pi }}{{r}^{\lambda -1}}\cos \frac{\theta }{2} \\ \end{align} \right\}$

(10)

根据式(8) ~式(10)可知，裂纹端邻域应力场只有Ⅰ,Ⅱ,Ⅲ,3种特定的应力分布规律. 裂纹端的应力奇异性以此为定义，即Ⅰ,Ⅱ,Ⅲ,3种裂纹端应力场对应Ⅰ型,Ⅱ型,Ⅲ型,3种裂纹端应力奇异性. Williams开启了裂纹端应力奇异性的研究.

1.4 弹性力学平面问题复变函数解法

Muskhelishvili的复变函数法^[8]是对带椭圆孔的无限平板的边值问题的十分有效的解法. 对于带理想裂纹的无限平板的边值问题，Muskhelishvili的复变函数法同样有效. 通过保角变换，把求解域变换到单位圆的外域，然后按单位圆域用复变函数理论求解.

设含单个椭圆孔的无限平板，在无限远处的应力状态为${{\sigma }_{x}}=\varepsilon P$${{\sigma }_{y}}=p,{{\tau }_{xy}}=q$,取映射函数

$Z=\omega (\zeta )=R(\zeta +\frac{m}{\zeta })$

(11)

将椭圆孔的外部映射到单位圆的外域.

当m=1时，映射函数(11)将理想裂纹的外部映射到单位圆的外域. 当带裂纹的无限平板受到单向拉伸时，得到裂纹端的应力分量^[9]由式(8)表示，且同时得到$K_{\rm I}=p\sqrt{\pi a}$.

由此可见，弹性理论平面问题复变函数解法是解决理想裂纹问题的理想工具^[10]，它提供裂纹端应力奇异性的解析解，以促进断裂力学研究的拓展和深化.

1.5 Williams界面裂纹端的应力震荡性

1959年，Williams^[11]把单体裂纹研究推广到双材料界面裂纹的齐次问题，用分离变量法求出界面裂纹尖端应力场的奇异性指数为出人意料的复数 $\left( -1/2+\text{i}\varepsilon \right),\varepsilon $ 称为震荡指数，是与双材料的弹性系数有关的常数. 在裂纹尖端前缘附近的应力可以下式表示

$\sigma \tilde{\ }{{r}^{-1/2}}\left( \begin{matrix} \sin \\ cos \\ \end{matrix} \right)\left( \lg r \right)$

(12)

由式(12)知，界面裂纹端应力场除了$r^{-1/2} \to \infty$外，还出现应力的震荡性.

1.6 England 界面裂纹端的自由面相互嵌入现象

1965年，England^[12]用复变函数法求解了带界面裂纹的双材料无限平板受单向拉伸σ的边值问题. 由弹性理论的解析解得到裂纹端附近的上下裂纹面的法向位移$u_{1y}$和$u_{2y}$之差的渐近式为

$\begin{align} & {{u}_{iy}}-{{u}_{2y}}=\frac{\sigma \sqrt{\alpha }}{2\left( 1+\alpha \right)}\left( \frac{1+{{\kappa }_{1}}}{{{\mu }_{1}}}+\frac{1+{{\kappa }_{2}}}{{{\mu }_{2}}} \right)\cdot \\ & {{\left( {{a}^{2}}-{{x}^{2}} \right)}^{1/2}}\cos \left( \varepsilon \lg \left| \frac{x+a}{x-a} \right| \right) \\ \end{align}$

(13)

式中,$\mu_1,\mu_2,\kappa_1,\kappa_2$是材料的弹性常数，ε是震荡指数，2a是裂纹长度,

$\alpha =\frac{{{\mu }_{1}}+{{\mu }_{2}}{{\kappa }_{1}}}{{{\mu }_{2}}+{{\mu }_{1}}{{\kappa }_{2}}}$

(14)

由式(13)看出：在界面裂纹端点后缘附近，上下裂纹面相互嵌入的皱纹状现象.这是界面裂纹端应力奇异性解中显示出来的另外一个病态现象.

2 断裂力学研究的开端

根据前述弹性理论对带理想裂纹的弹性连续介质问题的解析结果，从中推不出"含裂纹的韧性构件在载荷作用下发生脆性断裂的规律和条件". 断裂力学判据的产生，仅依靠弹性理论是不够的，这中间还有一个研究过程，这个过程要靠应用力学来完成.应用力学是在弹性理论裂纹分析的基础上通过假设来建立断裂力学判据的.

在美国自由轮钢板脆性断裂事故引起关注前，Griffith已经研究了玻璃的理论强度比实际强度大几个数量级的问题，他把原因归结为玻璃内部存在裂纹. Griffith的玻璃低应力脆断问题的研究，对自由轮钢板脆性断裂问题起到了参考的作用.

2.1 Griffith概念

1920年，Griffith^[13]对玻璃的理论强度和实际强度有数量级的差别提出了力学的解释. 玻璃的理论强度约为11 000 MPa,而实际强度仅为180 MPa. Griffith把原因归之于玻璃内部存在微小裂纹. 他认为裂纹扩展单位长度时，玻璃的表面能因自由表面积增加而增加，需有玻璃在裂纹扩展单位长度时所释放的应变能G来平衡. 当二者相等时，裂纹具有了扩展的条件.令玻璃的表面能为$\gamma_{\rm s}$,当应变能释放率G达到玻璃的表面能$\gamma_{\rm s}$

$G={{\gamma }_{\text{s}}}$

(15)

玻璃因裂纹扩展而断裂.

他用 Inglis^[5] 的关于短轴为零的椭圆孔应力集中的公式的解来计算G

$G=\frac{\pi {{\sigma }^{2}}a}{E}$

(16)

于是Griffith 得到一个玻璃强度公式

${{\sigma }_{\text{f}}}\sqrt{\pi a}=\sqrt{2{{\gamma }_{\text{s}}}E}$

(17)

式中，$\sigma_{\rm f}$是玻璃的实际强度，E是弹性模量，2a是裂纹的长度，$\gamma_{\rm s}$是玻璃的表面能.

Griffith关于玻璃脆断的解释在当时就受到极大的关注，被Timoshenko收入1933年出版的《弹性理论》^[14]书中.

2.2 Irwin和Orowan的推广

20世纪40年代末，美国海军研究实验室(NRL)的研究人员进行自由轮钢板脆性断裂事故问题的研究. Irwin注意到Griffith和Inglis的工作，但是他那时并不知道Westergaard的裂纹解也已存在了.

Griffith概念认为裂纹是玻璃低应力脆断的原因，Irwin^[15]和Orowan^[16]都认为含裂纹韧性构件脆性断裂问题与Griffith问题的差别在于玻璃是脆性材料，而钢板是塑性材料.他们将Griffith概念从脆性材料推广应用到塑性材料，来解决含裂纹韧性构件在载荷作用下发生脆性断裂的问题.对于塑性材料裂纹扩展时，除表面能外，需要计入塑性应变能.

他们从热力学的观点，提出了能量平衡原理

$\frac{dW}{dt}=\frac{dU}{dt}+\frac{dT}{dt}+\frac{dD}{dt}$

(18)

式中，W,U,T分别为外力功，应变能和动能，D为不可恢复的消耗能. 设G为裂纹扩展单位长度时所释放的应变能，$\gamma _{\rm p}$为裂纹扩展单位长度时耗散的塑性应变能，${{\gamma }_{\text{s}}}$裂纹扩展单位长度时增加的表面能. 对于金属材料，$\gamma_{\rm s} \ll \gamma_{\rm p}$，式(18)简化为

$G={{\gamma }_{\text{p}}}$

(19)

即当能量释放率G达到裂纹扩展时塑性应变能耗损率$\gamma _{\rm p}$，裂纹扩展.

式(19)用于判断金属材料的裂纹扩展时，有两点不方便，其一能量平衡原理要求裂纹扩展时系统是封闭的，没有其他能量进出. 其二是塑性应变能耗损率$\gamma _{\rm p}$难以实验测定或计算确定.

3 断裂力学的奠基工作 3.1 裂纹端应力场的光弹性实验

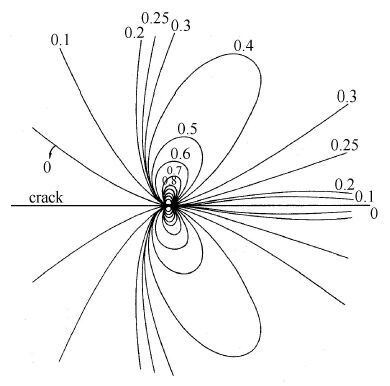
Post^[17] 进行了带裂纹试件的光弹性实验，并用有机玻璃试件进行了干涉条纹实验. 试件上的裂纹用薄刀片压入试件而成，形成的裂纹端的半径估计为2.54 μm.由光弹性实验得到等色线条纹图如图 1所示.用等色线条纹图和由干涉条纹实验得到的等厚条纹图可以确定二个主应力P和Q.

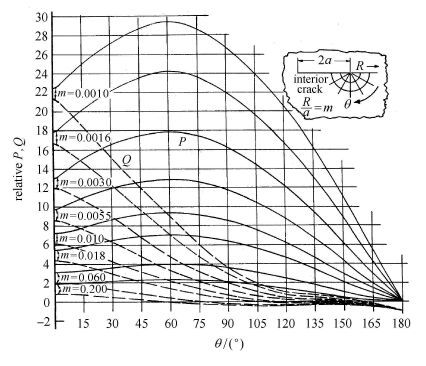
裂纹端应力分布的实验结果与Inglis的裂纹状椭圆孔应力集中解及Westergaard的理想裂纹解做了比较，结果是互相符合的. 说明Westergaard解对断裂力学是适用的. 图 2中的实线和虚线给出裂纹端主应力分布的理论曲线，实线和虚线分别为主应力P和Q，$m=R/a$,a为裂纹的半长，R为到裂纹端的距离.

不过，限于光弹性实验和干涉条纹实验的灵敏度，上述实验和理论结果的比较，并不包括紧靠裂纹端的微小邻域(例如：m<0.001).严格说来，Inglis的裂纹状椭圆孔应力集中解及Westergaard的理想裂纹应力奇异性解是有差别的，差别就在紧靠裂纹端的微小邻域内，否则这两个解就重合了.Westergaard的理想裂纹解在紧靠裂纹端的微小邻域内，有应力场的渐近式(式(8))，显示应力奇异性.而Inglis的裂纹状椭圆孔应力集中解在紧靠裂纹端的微小邻域内，没有奇异应力场的渐近式.

3.2 能量释放率和应力强度因子

在Post^[17]的论文中，Irwin^[18]看到了Wester- gaard^[6]论文的价值.他从Westergaard解出发，令$z=a+r{\rm e}^{{\rm i}\theta}$，在裂纹端邻域内，$\dfrac ra \ll 1$，得裂纹端应力场$\sigma_x$和$\sigma_y$的渐近表达式

$\left. \begin{align} & {{\sigma }_{x}}=\frac{{{K}_{\text{I}}}}{\sqrt{2\pi r}}\cos \frac{\theta }{2}(1-\sin \frac{\theta }{2}\sin \frac{3\theta }{2}) \\ & {{\sigma }_{y}}=\frac{{{K}_{\text{I}}}}{\sqrt{2\pi r}}\cos \frac{\theta }{2}(1+\sin \frac{\theta }{2}\sin \frac{3\theta }{2}) \\ \end{align} \right\}$

(20)

$K_{\rm I}$在渐近式中起到表征裂纹端邻域应力场的作用，$K_{\rm I}$的值决定整个裂纹端邻域的应力场应力的大小. $K_{\rm I}$称为应力强度因子.

用$\sigma_y$的渐近表达式计算应变能释放率$G_{\rm I}$，$d W$相当于裂纹扩展$d a$时释放的弹性应变能，B是板的厚度，E是杨氏模量

${{G}_{\text{I}}}=\frac{1}{B}\underset{da\to 0}{\mathop{\lim }}\,\frac{dW}{da}$

(21)

$dW=\frac{B}{E}K_{\text{I}}^{2}da$

(22)

由式(21)和式(22)得应变能释放率$G_{\rm I}$与应力强度因子$K_{\rm I}$的关系式

$K_{\text{I}}^{2}=E{{G}_{\text{I}}}$

(23)

3.3 线弹性断裂力学

含裂纹韧性构件脆性断裂问题促成了断裂力学的诞生. 断裂力学的诞生经历了一个概念发展的过程.

首先得到的是由Griffith 概念推广而来的能量平衡原理公式

$G={{\gamma }_{\text{p}}}$

(24)

Griffith采用Inglis 裂纹状椭圆孔应力集中解来计算应变能释放率G,Irwin 改用Westergaard理想裂纹应力奇异性解来计算应变能释放率 $G_{\rm I}$，于是

${{G}_{\text{I}}}={{\gamma }_{\text{p}}}$

(25)

成为裂纹扩展的条件.

考虑到塑性应变能耗损率$\gamma _{\rm p}$难以实验测定或计算确定，以实测的应变能释放率$ G_{\rm I}$的极限值$ G_{\rm IC}$取代之

${{G}_{\text{I}}}={{G}_{\text{IC}}}$

(26)

这就是线弹性断裂力学中的应变能释放率判据，$ G_{\rm IC}$由带裂纹试件的断裂实验测定，称为临界变能释放率，也叫断裂韧性. 这个判据虽然用到了应变能释放率，只是把应变能释放率当作裂纹扩展判据的力学参量. 应变能释放率判据(26)已经与原来的能量平衡的概念无关，也不再要求裂纹扩展时系统是封闭的.

另一方面，应力强度因子$K_{\rm I}$与应变能释放率$ G_{\rm I}$之间有关系式(23)，所以应力强度因子$K_{\rm I}$也可以当作裂纹扩展判据的力学参量

${{K}_{\text{I}}}={{K}_{\text{IC}}}$

(27)

这就是线弹性断裂力学中的应力强度因子判据，$ K_{\rm IC}$由带裂纹试件的断裂实验测定，或者

$K_{\text{IC}}^{2}=E{{G}_{\text{IC}}}$

(28)

考虑到Williams^[7]把裂纹端奇异应力场归结为 Ⅰ 型、 Ⅱ 型、 Ⅲ型. 于是，按 Ⅰ 型、Ⅱ 型、Ⅲ 型，采用应力强度因子 K建立的裂纹扩展判据^[19]分别为

${{K}_{\text{I}}}={{K}_{\text{ⅠC}}}{{K}_{\text{II}}}={{K}_{\text{IIC}}}{{K}_{\text{Ⅲ}}}={{K}_{\text{ⅢC}}}$

(29)

至此，线弹性断裂力学成功建立了应力强度因子判据，并迅速获得广泛应用^[2-3]. 许多裂纹问题的应力强度因子可从相关的手册^[20-21]中查到.

3.4 界面断裂力学

界面裂纹端的应力奇异性指数是一个复数($-1/2+ {\rm i}\varepsilon $),ε 为震荡指数. 界面裂纹端应力场除了按$r^{-1/2}$趋于无限大外，在渐近解中，还出现应力的震荡性^[11]和自由面相互嵌入现象^[12]，令人无法理解和接受. 界面断裂力学的判据研究因而受到延阻. 1988年，Rice^[22]撇开上述奇特现象，仍把线弹性断裂力学的概念推广到界面裂纹. 他用Muskhelishvili法求解了半无限长界面裂纹的无限域齐次问题，得到界面裂纹端应力场渐近式

$\begin{align} & {{\sigma }_{ij}}=\frac{1}{\sqrt{2\pi r}}[\text{Re}(K{{r}^{\text{i}\varepsilon }})\hat{\sigma }_{ij}^{\text{I}}(\theta ,\varepsilon )+ \\ & \text{Im}(K{{r}^{\text{i}\varepsilon }})\hat{\sigma }_{ij}^{\text{I}}(\theta ,\varepsilon )] \\ \end{align}$

(30)

式中,$\hat{\sigma }_{ij}^{\text{I}}(\theta ,\varepsilon )$和 $\hat{\sigma }_{ij}^{\text{II}}(\theta ,\varepsilon )$分别是Ⅰ型和Ⅱ型界面裂纹应力场的无量纲角分布函数,$K={{K}_{\text{I}}}+\text{i}{{K}_{\text{II}}}$是Rice 定义的界面裂纹复应力强度因子，$ K_{\rm I}$和${{K}_{\text{II}}}$分别是Ⅰ型和Ⅱ型的应力强度因子. Rice和 Sih^[23]用Muskhelishvili法求解了有限长中心界面裂纹受无限远平面应力$\sigma^\infty_{yy}$,$\sigma^\infty_{xy}$的边值问题，得到的复应力强度因子是

$K=(1+2\text{i}\varepsilon )(\sigma _{yy}^{\infty }+\text{i}\sigma _{xy}^{\infty }){{(2a)}^{-\text{i}\varepsilon }}\sqrt{\pi a}$

(31)

得到复应力强度因子的实部与虚部是

$\left. \begin{align} & {{K}_{\text{1}}}=\sqrt{\pi a}[\cos [\varepsilon \ln (2a)](\sigma _{yy}^{\infty }-2\varepsilon \sigma _{xy}^{\infty }) \\ & +\sin [\varepsilon \text{ln}(2a)](\sigma _{xy}^{\infty }+2\varepsilon \sigma _{yy}^{\infty })] \\ & {{K}_{\text{2}}}=\sqrt{\pi a}[\cos [\varepsilon \ln (2a)](\sigma _{yy}^{\infty }+2\varepsilon \sigma _{yy}^{\infty }) \\ & -\sin [\varepsilon \text{ln}(2a)](\sigma _{xy}^{\infty }-2\varepsilon \sigma _{xy}^{\infty })] \\ \end{align} \right\}$

(32)

由式(32)可见，界面裂纹端的Ⅰ型和Ⅱ型应力场总是相互耦合的，即使在单向拉伸或纯剪切载荷下，Ⅰ型和Ⅱ型应力场也总是同时出现的.

此外，由式(30)可见，复应力强度因子K的量纲是

$[K]=[\sigma ][{{L}^{1/2}}][{{L}^{-\text{i}\varepsilon }}]$

(33)

这个量纲与$-\text{i}\varepsilon $有关，ε是与双材料的弹性常数有关的震荡指数，所以按照Irwin 的办法，用复应力强度因子K来构建界面裂纹扩展判据会遇到量纲问题.

为了克服量纲困难，Suo等^[24-25]引入一个组合量$K{{l}^{\text{i}\varepsilon }}$ (l是任意设定的长度)，$K{{l}^{\text{i}\varepsilon }}$的量纲与单体裂纹的应力强度因子相同，它的模与原来的复应力强度因子K一样.但是问题还是没有完全解决，因为$K{{l}^{\text{i}\varepsilon }}$ 的实部和虚部和 l 有关，为此他们改用界面裂纹应变能释放率G来构建界面裂纹扩展判据. 他们定义界面裂纹应力场的相位角 .$\psi =\text{ta}{{\text{n}}^{-1}}[\text{Im}(K{{l}^{\text{i}\varepsilon }})/RE(K{{l}^{\text{i}\varepsilon }})]$ 于是，界面裂纹的应变能释放率判据为

$G(\psi )={{G}_{\text{C}}}(\psi )$

(34)

$ G_{\rm C}$是材料的界面裂纹临界应变能释放率. G和$ G_{\rm C}$都是ψ的函数.

嵇醒^[26] 注意到：复应力强度因子K 存在量纲问题，而界面裂纹端应力场的应力分量不存在量纲问题(见式(30)). 因此，令

$K=\hat{K}{{s}^{-\text{i}\varepsilon }}$

(35)

s为具有长度量纲的量，出现在复应力强度因子的公式中. 以式(31)为例，$s^{ - {\rm i}\varepsilon } = (2a)^{ - {\rm i}\varepsilon }$. 式(35)代入式(30)

$\begin{align} & {{\sigma }_{ij}}=\frac{1}{\sqrt{2\pi r}}\{\text{Re}[\hat{K}{{(\frac{r}{s})}^{\text{i}\varepsilon }}]\hat{\sigma }_{ij}^{\text{I}}(\theta ,\varepsilon )+ \\ & \text{Im}[\hat{K}{{(\frac{r}{s})}^{\text{I}\varepsilon }}]\hat{\sigma }_{ij}^{II}(\theta ,\varepsilon )\} \\ \end{align}$

(36)

由式(36)可见，$\hat K$表征界面裂纹端应力场，而且其量纲 $[\hat K]=[{\rm stress}][{\rm length}]^{1/2}$.所以，复应力强度因子$\hat{K}={{{\hat{K}}}_{\text{I}}}+\text{i}{{{\hat{K}}}_{\text{II}}}$ 可以直接用来构建界面裂纹扩展判据.

该文对界面裂纹端的Ⅰ型和Ⅱ型应力场总是相互耦合的问题，也做了相应的处理. 把界面裂纹的简单拉伸和纯剪切的混合型(Ⅰ/Ⅱ型)分别定义为准Ⅰ型和准Ⅱ型，准Ⅰ型的应力强度因子为$\hat K_{\rm QI}$，准Ⅱ型的应力强度因子的${{\hat{K}}_{\text{QII}}}$，准Ⅰ型和准Ⅱ型的界面裂纹扩展判据得以建立^[26]，

${{\hat{K}}_{\text{QI}}}={{\hat{K}}_{\text{QIC}}}$

(37)

${{\hat{K}}_{QII}}={{\hat{K}}_{QIIC}}$

(38)

混合型界面裂纹的扩展判据^[26]可用经验公式

${{(\frac{{{{\hat{K}}}_{\text{QI}}}}{{{{\hat{K}}}_{\text{QIC}}}})}^{2}}+{{(\frac{{{{\hat{K}}}_{\text{QII}\!\!\grave{\mathrm{o}}\!\!\text{ }}}}{{{{\hat{K}}}_{\text{QII}\!\!\grave{\mathrm{o}}\!\!\text{ C}}}})}^{2}}=1$

(39)

混合型界面裂纹的相位角定义为

$\hat{\psi }=\text{ta}{{\text{n}}^{-1}}\frac{{{{\hat{K}}}_{\text{QII}\!\!\grave{\mathrm{o}}\!\!\text{ }}}}{{{{\hat{K}}}_{\text{QI}}}}$

(40)

混合型界面裂纹扩展判据(39)与界面裂纹断裂实验的结果^{[25, 27]}比较，基本相符^[26].

至此，界面断裂力学也实现了以应力强度因子来建立判据.

界面断裂力学的综述见Banks-Sills^[28].

3.5 弹塑性断裂力学

20世纪60年代中，线弹性断裂力学判据建立后，弹塑性断裂力学的研究就开始了. 1965年，Wells^[29]提出了COD准则.该准则用裂纹顶端的张开位移 δ 为控制断裂的参量，并以 δ 达到裂纹顶端张开位移的临界值$\delta_{C}$作为断裂判据. 1968年,Rice^[30]提出了$J $积分.同年，Hutchinson^[31]，以及Rice和Rosegren^[32]用弹塑性全量理论对幂硬化材料的Ⅰ型裂纹问题进行了简化与分析，求得裂纹端应力场具有$r^{\tfrac1{n+1}}$ 奇异性(n为硬化指数)，裂纹端奇异应力场由塑性应力强度因子${{K}_{P}}$表征，并指出，塑性应力强度因子${{K}_{P}}$与外加应力σ之间的关系可通过J积分求出，因而J积分被用作表征该奇异应力场强度的控制参量，以J积分为特征参量的弹塑性断裂判据得以了建立，称为HRR理论.

$J={{J}_{\text{C}}}$

(41)

Sipes^[33]对弹塑性断裂力学的发展作了综述.

4 K_IC,J_IC测试与ASTM 的标准化

1959年，美国材料试验协会(ASTM)组织了一个特别技术委员会(E24)，以加强断裂力学的推广应用及规范断裂韧性的测试方法，不定期出版ASTM STC Report. 出版的报告中提到：用裂纹尖端应力场的应力强度因子K 建立裂纹扩展判据比用应变能释放率好.1964年的第5个报告对 ${K}_{\rm IC}$ 的测试方法做了改进，推荐试件上切削出缺口后，应再制作疲劳裂纹.由此可见E24对断裂力学起到的推动作用，及其对理论的鉴别力和洞察力.

${{K}_{\text{IC}}}$和${{K}_{\text{IC}}}$的测试结果，对断裂力学应用于结构的防断设计是至关重要的，${{K}_{\text{IC}}}$和${J}_{\rm IC}$的测试标准是${K}_{\rm IC}$和${J}_{\rm IC}$的测试结果可靠性的保证. 美国材料试验协会于1970年颁发了世界第一个断裂韧性试验标准ASTME399-70T. ASTM E1820-11是2011年的${{K}_{\text{IC}}}$试验标准^[34]，ASTM E399-09e2是2011年的${J}_{\rm IC}$的试验标准^[35].

Zhu等^[36]对金属材料的断裂韧性测试研究作了综述.

5 断裂力学的判据原理

Irwin^[18]提到："在二战和战后对断裂力学的研究中，分享了应用力学的成熟(During and subsequent to the recent World War,investigations fracturing have shared in the general growth of applied-mechanics)".那么，应用力学如何在断裂力学的研究中起到作用呢？应用力学的作用是帮断裂力学寻找判据原理.

固体力学判据原理的依据是应力原理. 应力原理认为材料的破坏由一点的应力状态决定，而与此点之外的应力状态无关. 固体力学中的古典强度理论就是这样提出来的，判据的准确性由实验来检验.

Ⅰ型裂纹端奇异应力场$(\sigma^{\rm I}_{ij})_{r\to 0} \to \infty$,不论施加的载荷任意小，裂纹端的应力还是无限大，上述固体力学判据原理不再适用. 断裂力学的判据改用$K_{\rm I}$为控制参量，断裂力学的$K_{\rm I}$判据的准确性也是由实验验证来确认的. 据此，断裂力学的判据原理变成：材料的破坏由裂纹端的应力强度因子判定.

6 断裂力学判据中尚存在的问题 6.1 裂纹角的预测问题

混合型的裂纹判据中，需包括裂纹扩展方向(开裂角)的预测. 1963 年，Erdogan和 Sih^[37]提出最大拉应力理论，1972 年，Palaniswamy 等^[38]提出最大能量释放率理论，1973年，Sih^[39]提出应变能密度理论. 3种开裂角预测方法的结果互有差别，与实验比较，难分优劣^[40].

6.2 界面裂纹端的震荡奇异性和相互嵌入问题

迄今为止，界面裂纹端的应力震荡性和裂纹面相互嵌入现象仍然是未被阐明的问题. 不明白为什么弹性理论的严格的数学分析得到的解中，会有这样的现象出现在解中，也不明白为什么界面断裂力学在建立判据的时候，避开了这些现象，也能得到满意的判据. 要使得界面断裂力学的判据有充分的理论根据，需要对界面裂纹端的震荡奇异性和相互嵌入问题作透彻的说明.

6.3 裂纹端弹塑性应力场的分析问题

弹塑性断裂力学的COD判据^[29]采用D-M模型，假设裂纹端前缘的塑性区为狭条形，认为材料是理想弹塑性的，塑性区内的应力等于屈服应力，换言之，裂纹尖端不存在应力奇异性.而弹塑性断裂力学的J判据以材料是硬化弹塑性，裂纹端存在应力奇异性为依据. HRR的弹塑性裂纹分析^[31-32]得出的奇异性指数为$- 1/(n+1)$,n 为强化指数.目前这二个判据是并存的，任人选用.J判据所以不能胜过COD判据的原因是由于弹塑性裂纹分析是非线性的，得不到精确解，HRR的弹塑性裂纹分析作了一些简化，简化对问题带来的误差未能确定是否在许可范围内.由此可见，需要对裂纹端弹塑性应力场作出有误差估计的可靠的近似分析，以确保简化对裂纹端奇异性的影响在许可范围内.

7 Sinclair的应力奇异性研究

1980年起，Sinclair等^[41-42]关注断裂力学的应力奇异性的研究，2004年，Sinclair^[43-44]对弹性理论应力奇异性作了全面的综述，阐明他对应力奇异性的观点.他的研究，集中在怎样改进弹性理论建模来去除应力奇异性，使得断裂力学能够免除应力奇异性的困扰.虽然他的研究未能对断裂力学产生积极的效果，但是，他对应力奇异性研究的方向是独树一帜的，体现了他的研究思想的前瞻性.他所研究的问题是：(1) 应力奇异性的源^[45]; (2) 去除应力奇异性^[42]; (3)应力强度因子的物理意义^[43].

7.1 应力奇异性的源

断裂力学中关于应力奇异性的已有研究集中在裂纹端的奇异应力场，而未曾涉及裂纹端的奇异应力场从何而来. Sinclair要知道应力奇异性的源，就是要进一步探求应力奇异性的本质，就是要知道裂纹端的奇异应力场是真实的，还是不真实的.

因为裂纹端的奇异性出现在弹性理论的解中，所以应力奇异性的源在弹性理论的数学模型中^[43].可是在弹性理论的几何、本构和静力学方程中没有找到应力奇异性的源，所以应力奇异性的源应该是在边界条件中.不过，迄今尚未在边界条件中确切找到应力奇异性的源.

7.2 去除应力奇异性

去除应力奇异性的研究本身就是一种对应力奇异性的看法和态度，认为应力奇异性不是一种力学的正常，认为应力奇异性去除之后，才能恢复力学的正常. 如果能做到去除应力奇异性，断裂力学中遇到的麻烦问题也就一笔勾销了.

去除应力奇异性的研究由来已久，人们想了各种办法，实现去除应力奇异性的研究. 例如：Barenblatt^[46]的分子间内聚力模型，Sinclair ^[47]的cohesive stress-separation law模型等，均是在弹性理论数学模型之外引入额外的附加条件来达到去除应力奇异性的目的.

Sinclair^[43]提出去除应力奇异性的目的是要求得裂纹端点处实际存在的有限值的应力，他认为裂纹端点处存在的有限值的应力才是控制裂纹扩展的力学参量.如果能够证明裂纹端点处存在有限值的应力，那么，裂纹扩展判据也可以按照应力原理来建立了.按照这个要求，可以看到，所有上述去除应力奇异性的方法，都不符合这个要求.符合要求的去除应力奇异性的研究至今没有进展.

应力奇异性是由理想裂纹伴随而来的. Westergaard的理想裂纹解的裂纹边界条件是

${{\sigma }_{\theta }}={{\tau }_{r\theta }}=0,\theta =\pm \pi $

(42)

如上节假定所述，裂纹端前缘的应力是

${{\sigma }_{\theta }}={{\sigma }_{\text{I}}},\theta =0,r\to {{0}^{+}}$

(43)

裂纹端应力奇异性由此产生.

Inglis 的椭圆孔应力集中解的孔边边界条件是

${{\sigma }_{n}}={{\tau }_{nt}}=0,\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1$

(44)

椭圆孔长轴端的应力是

${{\sigma }_{y}}={{\sigma }_{\max }},y=0,x\to {{a}^{+}}$

(45)

在椭圆孔长轴端值出现应力集中，没有应力奇异性.

由此可见，Inglis 的裂纹状椭圆孔($0\ne b\to 0$)应力集中解做到了去除裂纹端的应力奇异性. 可是，裂纹状椭圆孔应力集中的弹性解得到的结果还是无限大应力，不能用作判据的力学参量，所以还是没有达到Sinclair 的去除应力奇异性后要得到有限值应力的要求.

按照对实际的疲劳裂纹的测量，把疲劳裂纹处理成等宽钝头孔^[48](即实际裂纹模型)的做法，能得到的结果与椭圆孔类似.

7.3 应力强度因子的物理意义

在去除应力奇异性没有成功的情况下，退路是继续采用应力强度因子判据^[43].为此，至少要能阐明应力强度因子的物理意义，说明为什么应力强度因子可以作为裂纹扩展的力学参量，使得断裂力学的K判据原理具有力学的物理基础.

${{K}_{\text{I}}}$来自Ⅰ型裂纹端奇异应力场渐近表达式，可以写成

${{K}_{\text{I}}}={{(\frac{d\sigma _{ij}^{\text{I}}}{d{{r}^{-1/2}}})}_{r\to 0}}$

(46)

由此可见，应力强度因子${{K}_{\text{I}}}$是裂纹端的奇异应力$\sigma _{ij}^{\text{I}}$对$ r^{-1/2}$的导数. 换言之，应力强度因子除了它可以表征裂纹端应力场外，难以根据式(46)给出另外的具有明确物理意义的力学定义.

8 双材料角界面端应力奇异性 8.1 界面端应力奇异性指数

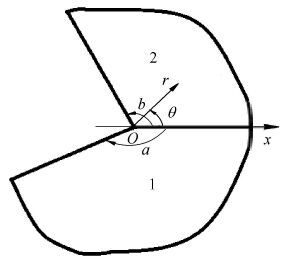
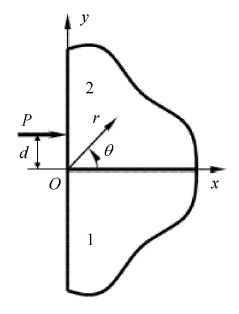
双材料角由二个不同材料的锲角平面接合而成(图 3)，锲角平面的锲角为a和b，两种材料1和2的Dundurs常数^[49]为α和β.Dundurs常数是2种材料的4个弹性常数的组合，见下式

$\alpha =\frac{{{\mu }_{1}}(1-{{\nu }_{2}})-{{\mu }_{2}}(1-{{\nu }_{1}})}{{{\mu }_{1}}(1-{{\nu }_{2}})+{{\mu }_{2}}(1-{{\nu }_{1}})}$

(47)

$\beta =\frac{1}{2}\frac{{{\mu }_{1}}(1-2{{\nu }_{2}})-{{\mu }_{2}}(1-2{{\nu }_{1}})}{{{\mu }_{1}}(1-{{\nu }_{2}})+{{\mu }_{2}}(1-{{\nu }_{1}})}$

(48)

Bogy ^[50-51]，Hein 等^[52]采用Airy应力函数和Mellin变换，求解了双材料角的平面特征值问题. 双材料角的界面端会出现应力奇异性，但也可能不出现应力奇异性. 界面端处的界面应力以下式表示

${{\tau }_{ij}}=\underset{r\to 0}{\mathop{\lim }}\,{{K}_{ij}}{{r}^{\lambda }}$

(49)

式中，λ为应力奇异性指数，K_ij 是界面端应力场的应力强度因子，r是界面上的场点到界面端的距离. 双材料角界面端的奇异性指数λ 不是常数，而是与Dundurs常数α,β及双材料角的2个顶角a和b 有关的函数，即

$ \lambda =\lambda (\alpha ,\beta ;a,b) $

(50)

双材料角的奇异性指数一般以复数的形式来表示：$\lambda =\gamma +\text{i}\varepsilon $. 根据γ和ε的值，双材料角可分为3种情形：

(1) 无奇异性 ($\gamma =0,\varepsilon =0$);

(2) 变指数奇异性 (-1 < γ <0,ε= 0);

(3) 变指数振荡奇异性 (-1 < γ <0,ε ≠ 0).

由此可见，双材料角的应力奇异性是弹性理论中最复杂的应力奇异性.

虽然双材料角界面上没有裂纹，但是和断裂力学却有着密切的关系. 当双材料角的界面端发生了界面脱粘，界面裂纹就形成了. 另外，如果$a=b=\pi$，则双材料角问题就变为界面裂纹问题，如果$a=b=\pi ,\alpha =\beta =0$，则双材料角问题就变成单体裂纹问题.

8.2 双材料角界面端初始脱粘判据的研究

Gradin^[53]用界面端应力强度因子建立90°/90°双材料角的初始脱粘判据，Akisanya 和 Fleck ^[54],Reedy ^[55],Labossiere 等^[56],Nied ^[57]等以同样方法研究了给定锲角的双材料角的初始脱粘判据.

要建立适用于任意锲角的双材料角界的初始脱粘判据，却遇到了前所未有的困难，困难来自界面端奇异性指数不是常数.以Dundurs常数$\alpha =0.7\text{,}\beta =0$的双材料为例，90°/90°界面端的奇异性指数是λ = -0.234 6，其应力强度因子的量纲是${{K}_{1}}]=[\sigma ][{{L}^{1/2}}][{{L}^{-0.2346}}]$,而90°/180°界面端的奇异性指数是λ = - 0.421 3，其应力强度因子的量纲是$[{{K}_{2}}]=[\sigma ][{{L}^{1/2}}][{{L}^{-0.4213}}]$. 它们的临界应力强度因子$K_{\rm cr1} $和$K_{\rm cr2}$因量纲不同而无法相互比较及换算.

嵇醒^[58]对90°/90°和90°/180°界面端建立了$K_{\rm cr1} $和$K_{\rm cr2}$的关系

${{K}_{\text{cr2}}}={{K}_{\text{cr1}}}\frac{\rho _{\text{T1}}^{{{\lambda }_{1}}}}{\rho _{\text{T2}}^{{{\lambda }_{2}}}}$

(51)

式中，λ₁和λ₂分别是90°/90°和90°/180°界面端的奇异性指数^[58].

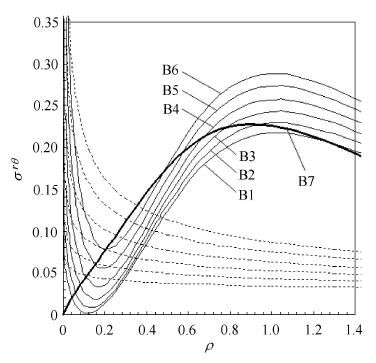
8.3 90°/90°双材料角界面端应力奇异性的源

Bogy^[59] 采用Airy应力函数和Mellin变换，求解了90°/90°双材料角的受集中力作用的边值问题(图 4)，得到了界面应力的严格解和渐近解.嵇醒^[60]用Bogy^[59]的严格解和渐近解计算了B1~B7七种90°/90°双材料角的界面应力，界面剪应力分布如图 5所示. 实线是严格解，虚线是渐近解.

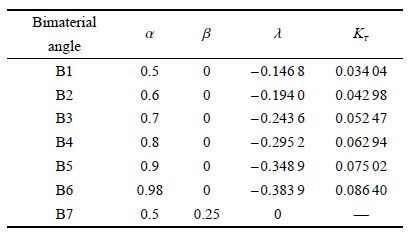
B1到B7 七种双材料的Dundurs常数α,β 和奇异性指数λ见表 1. $K_\tau $是界面端剪应力强度因子.

由表 1及图 5可见，B1到B6的90°/90°双材料角的界面端存在应力奇异性，在界面端界面剪应力趋于无限大. 而B7的90°/90°双材料角的界面端不存在应力奇异性，在界面端界面剪应力等于零.需要注意的是在90°/90°双材料角的界面端没有任何应力集中的因素(见图 4).由此可见，B1到B6的90°/90°双材料角界面端的应力奇异性不是应力集中造成的，90°/90°双材料角应力奇异性的无限大界面剪应力不是无限大应力集中系数造成的. 那么，B1到B6的90°/90°双材料角的界面端的无限大界面剪应力是从哪里来的？由图 4可见，由集中力P=1引起的在界面端的界面剪应力不可能是无限大.界面端剪应力的数值只有两种可能，或者由于自由边界条件而等于零，如B7，或者由于2种材料的弹性差异而在界面端产生有限值的剪应力，如B1 到B6. 如果B1 到B6的90°/90°双材料角界面端的界面剪应力为有限值，而界面端的自由面上又给定剪应力为零，于是，界面端点剪应力互等定律不满足，也就是该点的平衡条件不完全满足. 显然，这样的界面端点就成为边界上的一个奇点.于是，合理的推断^[60]是：正是这个剪应力互等定律不满足的奇点成为990°/90°界面端应力奇异性的源，导致应力奇异性解，并在界面端出现无限大剪应力.

9 裂纹端应力奇异性的源 9.1 关于裂纹端应力奇异性的源的讨论

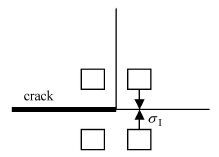
现在，参考90°/90°界面端应力奇异性的产生机理，以Ⅰ型裂纹为例，来讨论裂纹端应力奇异性的产生机理.

假设在裂纹前缘存在有限值拉应力${{\sigma }_{\text{I}}}$(图 6)，裂纹后缘为自由裂纹面，在裂纹端前后缘的伸长应变出现间断，使得弹性理论连续性条件不能满足，裂纹端点成为伸长应变间断的奇点，这个奇点使得弹性理论的解里出现Ⅰ型应力奇异性.换言之，裂纹前缘存在的有限值拉应力${{sigma }_{ ext{I}}}$导致裂纹端的应力奇异性及表征渐近应力场的应力强度因子K_Ⅰ. 这个假设需要有足够的理论证据来证实.

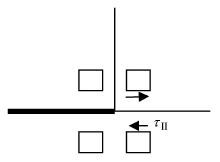
对于Ⅱ型和 Ⅲ型裂纹端应力奇异性的产生机理，可以作同样的讨论 (见图 7和图 8).

9.2 去除裂纹端应力奇异性的讨论

基于裂纹端应力奇异性的源的讨论，可以看到，只要能求出导致应力奇异性的实际存在于裂纹前缘的有限值拉应力${{\sigma }_{\text{I}}}$，就找到了导致裂纹扩展的应力分量. 所以，研究的目标应该是求出有限值拉应力${{\sigma }_{\text{I}}}$，而不仅仅是想方设法来去除应力奇异性. 或者，去除应力奇异性的研究应该以得到有限值拉应力${{\sigma }_{\text{I}}}$为目的.

9.3 关于裂纹端应力强度因子的物理意义的讨论

以Ⅰ型裂纹端为例，如果裂纹端应力奇异性产生的源是由于裂纹端拉应力${{\sigma }_{\text{I}}}$造成二側的应变间断，裂纹端应力奇异性表现为以K_Ⅰ表征的裂纹端奇异应力场. 所以，K_Ⅰ的出现是由于${{\sigma }_{\text{I}}}$的存在，换言之，${{\sigma }_{\text{I}}}$对裂纹扩展的控制，实际上是${{\sigma }_{\text{I}}}$在起作用. 因此，裂纹端应力强度因子K_Ⅰ的物理意义可以通过裂纹端应力${{\sigma }_{\text{I}}}$来理解.

10 总结与展望 10.1 应力强度因子判据

断裂力学取得成功，主要因为做了三方面的研究：即数学弹性理论方面、应用力学方面和材料力学试验方面.数学弹性理论着重研究的是应力奇异性，应用力学着重研究的是判据原理，材料力学试验着重研究的是断裂韧性.

断裂力学的数学弹性理论方面从裂纹问题的求解入手，揭示裂纹端应力奇异性. 应用力学着重研究的是判据原理.由于裂纹端的应力奇异性，固体力学的应力原理不能成为断裂力学建立判据的依据，只能从裂纹端奇异性应力场中提取别的力学参量.应力强度因子K的发现，是断裂力学取得成功的关键.断裂力学建立应力强度因子判据取得成功，由此形成了一种新的判据原理------K原理.材料力学试验为应力强度因子判据提供实验验证，提供临界应力强度因子数据，并保证测得的临界应力强度因子是材料本身的断裂韧性性能.

10.2 裂纹端应力奇异性的源

断裂力学是固体力学中的一个新分支，又是一个与固体力学不完全相同的分支. 应力奇异性赋予断裂力学很不一般的特殊性. 基于应力原理的强度理论在固体力学中一向是通行无阻的，可是在目前的断裂力学中却行不通了.

然而，断裂力学还在继续发展，对裂纹端的应力奇异性的研究还要深入下去. 裂纹端的应力奇异性的源是一个新问题，是一个能把断裂力学的研究引向深入的问题. 迄今为止，弹性理论只研究如何按照边界条件求得相应的解答，而不研究为何按理想裂纹的边界条件求得的解答会含有应力奇异性；也不研究裂纹端的无限大奇异应力是物理真实的，还是仅仅出现在数学解的表达式中. 然而，缺少了这些研究，断裂力学的判据研究就会深入不下去.

假设在裂纹前缘存在有限值拉应力${{\sigma }_{\text{I}}}$，则可以用应变间断来解释为什么裂纹端存在应力奇异性. 但是，在Ⅰ型理想裂纹问题的严格解和渐近解中，都没有给出有限值的裂纹端应力${{\sigma }_{\text{I}}}$因此，用什么办法可以把有限值的裂纹端应力${{\sigma }_{\text{I}}}$找到，是弹性理论的一个值得研究的重要问题.

如果能够证明：裂纹端的Ⅰ型应力奇异性确是由于裂纹端应力${{\sigma }_{\text{I}}}$ (有限值)与裂纹端应变间断所造成的，而且的确是裂纹端应力${{\sigma }_{\text{I}}}$ 控制裂纹的扩展. 那么，K_Ⅰ起到的作用，实际上是${{\sigma }_{\text{I}}}$ 在起作用. 换言之，在断裂力学中，应力原理并未失效，K原理和应力原理是互通的.

10.3 裂纹端应力奇异性弹塑性分析

有了${{\sigma }_{\text{I}}}$，前面提到的弹塑性断裂力学判据问题，就有了新的研究思路. 设裂纹端存在应力${{\sigma }_{\text{I}}}$，而裂纹扩展时临界的裂纹端应力是σ_IC. 若σ_IC小于材料的屈服应力σ_s时，则断裂是脆性的，属于线弹性断裂力学. 如果σ_IC> σ_s，则断裂是弹塑性的，属于弹塑性断裂力学. 此时，裂纹端的塑性区是大于σ_s的裂纹端应力${{\sigma }_{\text{I}}}$产生的，弹塑性裂纹端的应力奇异性是裂纹端的弹塑性应变的间断造成的，裂纹端的应力强度因子K_p需用裂纹端在${{\sigma }_{\text{I}}}$作用下的弹塑性应力奇异性分析来计算.