随着机械设备的高速化、精密化,如何建立具有高计算效率的非线性大变形多柔体系统求解策略已成为当务之急.在多柔体系统动力学领域,浮动坐标法[1] 应用最为广泛,该方法将构件弹性变形视为浮动坐标系大范围运动和相对于该坐标系弹性变形的叠加,利用刚体坐标和柔性体节点坐标或模态坐标建立动力学模型. 但该方法也存在缺陷[2-3],例如: 慢变大幅值的刚体坐标和快变微幅的弹性变形坐标会使数值计算病态;边界计算不精确;基于小变形、小转动假设,描述柔性体大变形必须考虑高次耦合项等. 为解决上述问题,Shabana等[4-5]基于有限元与连续介质力学理论提出了绝对节点坐标法(absolute nodal coordinate formulation,ANCF).该方法将单元节点坐标定义在全局坐标系下,采用斜率矢量代替节点转角坐标,具有常数质量阵,不存在科氏力、离心力等.ANCF可以精确处理柔性多体系统的非线性大变形问题,被视为多体系统动力学历史上的一个重要进展[6].
ANCF的求解策略目前主要依据拉格朗日方程、哈密顿原理等分析力学方法,将多体系统动力学问题转换为数学的微分-代数方程(differential algebraic equation, DAE)形式,再根据Baumgarte方法、Newmark方法、HHT方法、广义a方法、增广拉格朗日方法等进行求解[7].但是DAE存在违约问题,在误差累积过程中可能出现精度降阶[8].并且相比于浮动坐标法一般采用的模态坐标,ANCF采用的有限元节点坐标会使方程组维数大幅提高,因此其计算也会更加复杂.
许多学者对ANCF的计算效率问题进行了研究,并取得了一定的成果. Shabana [9] 对ANCF广义雅可比矩阵进行QR分解,利用得到的分解矩阵进行坐标转换,将质量矩阵转换成单位阵,使计算效率提高.但该方法不能按照传统有限元方法进行单元集成. Yakoub等[10] 对ANCF质量矩阵进行Cholesky分解,同样将质量矩阵归一化,但解决了上述单元集成的问题. Garcia-Vallejo等[11] 提出不变矩阵法,将ANCF非线性刚度矩阵分解成常数阵与迭代矩阵之和,简化了雅可比矩阵的运算. 但该方法在处理大规模问题时需消耗很大内存以提前存储预处理常数矩阵. Hussein等[12] 利用HHT方法求解ANCF指标$-3$的DAE,通过与显示ADAMS方法对比发现HHT方法在求解具有高频响应的系统动力学问题时效率更高.Tian等[13] 从约束方程违约、计算效率等方面对ANCF的多种DAE求解算法进行了详细的比较,并基于增广拉格朗日方程提出了一种高效算法.刘铖等[14]采用第一类Piola-Kirchhoff应力张量方法推导弹性力和雅可比矩阵的解析表达式,大幅提高了ANCF的计算效率.近年来,也有一些学者[15-21] }对ANCF方法效率进行了研究.
在多体系统算法方面,传统的方法如牛顿-欧拉法、拉格朗日法、凯恩方法 [22]、Birkhoff方法 [23] }等,其算法复杂度为O(n2)或O(n3).为了提高计算效率,得到算法复杂度更低的算法,学者们进行了大量的研究[24]. Featherstone [25-26] 首先创造性提出复杂度为$O(n)$的铰接体算法. Rodriguez [27] 将Featherstone算法和随机估计理论中的Kalman滤波及平滑方法相结合提出了空间算子代数方法. 此后,Rodriguez等 [28-31] 完善了一般拓扑结构多体系统和多柔体系统的空间算子代数理论,并将其推广应用.
本文提出了一种$O(n)$算法复杂度的递推绝对节点坐标法RANCF.该方法保留了ANCF可精确描述柔性体大变形的优点,同时极大地提升了算法效率,是一种高效的非线性大变形多柔体系统求解方法.本文主要由以下几个部分构成:第一部分阐述递推绝对节点坐标法理论;第二部分通过算例进行验证说明;第三部分是本文的结论和展望.
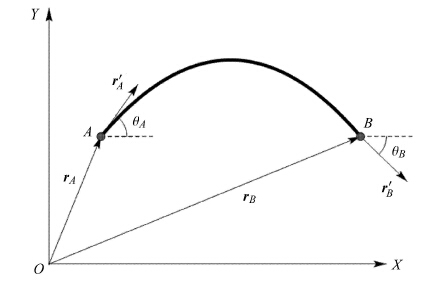
1 递推绝对节点坐标法RANCF 1.1 Shabana一维两节点梁单元模型递推绝对节点坐标法适用于各种ANCF有限单元,为了阐述方便,本文以Shabana一维梁单元 [4] 为例进行推导, Shabana一维梁单元如图 1所示.
|
图 1 Shabana一维梁单元 Figure 1 Shabana one-dimensional beam element |
Shabana 选取绝对坐标系下梁单元两端点的位置坐标和斜率矢量作为该单元的节点坐标,即
| $ { e} = \left[\!\!\begin{array}{c} { r}_A \\ { r}_B \\ { r}'_A \\ { r}'_B \end{array}\!\! \right] ,\ \left.\!\! \begin{array}{l} { r}'_A = \dfrac{\partial { r}_A }{\partial s} \\ { r}'_B = \dfrac{\partial { r}_B }{\partial s} \end{array}\!\! \right\} $ | (1) |
其中$s$为梁单元未变形时沿轴线的单元局部坐标,$s \in \left[ 0 l \right]$,$l$为单元初始长度. 绝对坐标系下梁单元上任意一点的位置坐标可以表述为
| $ { r} = { S e} $ | (2) |
其中梁单元形函数为
| $ { S} = \left[\!\! \begin{array}{c} \left( {1 - 3\xi ^2 + 2\xi ^3} \right){ I}_2 \\ l\left( {\xi - 2\xi ^2 + \xi ^3} \right){ I}_2 \\ \left( {3\xi ^2 - 2\xi ^3} \right){ I}_2 \\ l\left( {\xi ^3 - \xi ^2} \right){ I}_2 \end{array} \!\! \right]^{\rm T} ,\xi = \dfrac{s}{l} $ | (3) |
其中${ I}$为单位阵,该单元的质量阵为
| $ { M}_E = \int_V \rho { S}^{\rm T}{ S}d V =\\ \quad \left[\!\!\begin{array}{cccc} \dfrac{13}{35}{ I}_2 & \dfrac{11l}{210}{ I}_2 & \dfrac{9}{70}{ I}_2 & - \dfrac{13l}{420}{ I}_2 \\ & \dfrac{l^2}{105}{ I}_2 & \dfrac{13l}{420}{ I}_2 & - \dfrac{l^2}{140}{ I}_2 \\ & & \dfrac{13}{35}{ I}_2 & - \dfrac{11l}{210}{ I}_2 \\ {\rm symmetric} & & & \dfrac{l^2}{105}{ I}_2 \end{array} \!\! \right] $ | (4) |
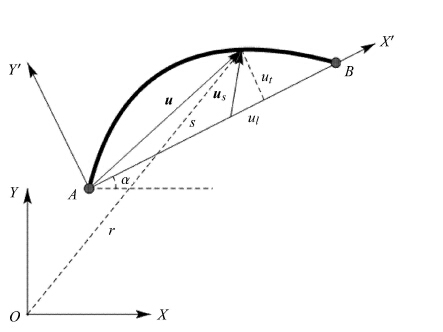
如图 2所示,在梁单元端点处建立随体坐标系,其中$X'$轴为梁单元两端点连线.
|
图 2 一维梁单元变形 Figure 2 Deformation of a one-dimensional beam element |
因此,梁单元上任意一点的变形在随体坐标系下的描述为
| $ { u}_s = \left[\!\!\begin{array}{c} {u_l } \\ {u_t } \end{array}\!\! \right] = \left[\!\! \begin{array}{cc} {{\rm cos}\alpha } & {{\rm sin}\alpha } \\ { - {\rm sin}\alpha } & {{\rm cos}\alpha } \end{array} \!\!\right]\left( {{ r} - { r}_A } \right) - \left[\!\! \begin{array}{c} s \\ 0 \end{array} \!\! \right] $ | (5) |
其中$\alpha $为随体坐标系相对于惯性系的转角. 根据线弹性模型,梁单元弹性势能可表述为
| $ U = \dfrac{1}{2}\int_0^l \left[{Ea\left( {{u}'_l } \right)^2 + EI\left( {{u}"_t } \right)^2} \right] d s \\ \left( {{u}'_l = \dfrac{\partial u_l }{\partial s},{u}"_t = \dfrac{\partial ^2u_t }{\partial s^2}} \right) $ | (6) |
其中,$E$是弹性模量,$a$为梁的横截面积,$I$为梁的截面惯性矩.将式(2)和式(5)代入式(6),可以得到梁单元的弹性力为
| $\begin{align} & {{F}_{EK}}={{K}_{E}}e=\left( \frac{\partial U}{\partial e} \right)=\left( \text{co}{{\text{s}}^{2}}\alpha \right)\left( {{A}_{11}}+{{B}_{22}} \right)e+ \\ & {{e}^{\text{T}}}\left( {{A}_{11}}+{{B}_{22}} \right)\cdot e\left( \text{cos}\alpha \frac{\partial \left( \text{cos}\alpha \right)}{\partial e} \right)+\left( \text{si}{{\text{n}}^{2}}\alpha \right) \\ & \left( {{A}_{22}}+{{B}_{11}} \right)e+\text{T}\left( {{A}_{22}}+{{B}_{11}} \right)e\left( \text{sin}\alpha \frac{\partial \left( \text{sin}\alpha \right)}{\partial e} \right)+ \\ & \left( \text{sin}\alpha \text{cos}\alpha \right)\left( {{A}_{12}}+{{A}_{21}}-{{B}_{12}}-{{B}_{21}} \right)e+ \\ & \frac{1}{2}{{e}^{\text{T}}}\left( {{A}_{12}}+{{A}_{21}}-{{B}_{12}}-{{B}_{21}} \right)\cdot e\left( \text{sin}\alpha \frac{\partial \left( \text{cos}\alpha \right)}{\partial e}+\text{cos}\alpha \frac{\partial \left( \text{sin}\alpha \right)}{\partial e} \right) \\ & -\left( \text{cos}\alpha \right)A_{1}^{\text{T}}-\left( \text{sin}\alpha \right)A_{2}^{\text{T}}-{{A}_{1}}e\left( \frac{\partial \left( \text{cos}\alpha \right)}{\partial e} \right)-{{A}_{2}}e\left( \frac{\partial \left( \text{sin}\alpha \right)}{\partial e} \right) \\ \end{align}$ | (7) |
其中,${ A}_{11} ,{ A}_{12} ,{ A}_{21} ,{ A}_{22} ,{ B}_{11} ,{ B}_{12} ,{ B}_{21} ,{ B}_{22} ,{ A}_1 ,{ A}_2 $为常数阵,其具体形式可参考文献[4].根据虚功率原理,当梁单元上受到外力${ F}$时,其对应的单元节点力为
| $ { F}_E = { S}^{\rm T}{ F} $ | (8) |
特别地,重力所对应的单元节点力为
| $ { F}_{EG} = mg\left[\!\!\begin{array}{cccccccc} 0 & {\dfrac{1}{2}} & 0 & {\dfrac{l}{12}} & 0 & {\dfrac{1}{2}} & 0 & { - \dfrac{l}{12}} \end{array} \!\! \right]^{\rm T} $ | (9) |
采用绝对节点坐标法处理柔性体时,单元的质量阵为常数阵,刚度阵为强非线性阵,其离心力和科氏力为0,所以单元的动力学方程为
| $ { M}_E \ddot{ e} + { K}_E { e} = { F}_E $ | (10) |
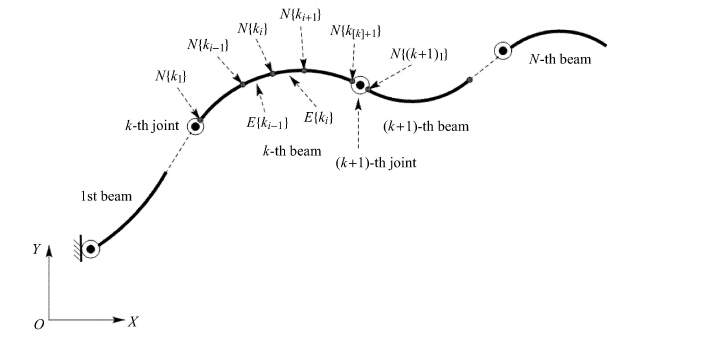
如图 3所示,一个由Shabana一维两节点梁单元组成的链式多柔体系统,其柔性体数目为$N$,从基座向端部对柔性体编号,依次为$1,2,\cdots ,N$. 第$k$个柔性体的单元数记为$\left[k \right]$,对每个单元顺序编号$E\left\{ {k_1 } \right\},E\left\{ {k_2 } \right\},\cdots ,E\left\{ {k_{\left[k \right]} } \right\}$. 同样第$k$个柔性体的节点数为$\left[k \right] + 1$,对每个节点顺序编号${N}\left\{ {k_1 } \right\},{N}\left\{ {k_2 } \right\},\cdots ,{N}\left\{ {k_{\left[k \right] + 1} } \right\}$.
|
图 3 RANCF多柔体系统 Figure 3 The flexible multibody system by RANCF |
首先分析柔性体内有限单元之间的运动学递推关系. 梁单元中每个节点的节点速度记为
| $ { V}_N \left\{ {k_i } \right\} = \left[\!\!\begin{array}{cccc} {\dot {x}\left\{ {k_i } \right\}} & {\dot {y}\left\{ {k_i } \right\}} & {\dot {{x}'}\left\{ {k_i } \right\}} & {\dot {{y}'}\left\{ {k_i } \right\}} \end{array} \!\! \right]^{\rm T} $ | (11) |
所以第$k_i $个单元的单元速度可以表述为
| $ { V}_E \left\{ {k_i } \right\} = \dot{ e}\left\{ {k_i } \right\} = \left[\!\!\begin{array}{c} {{ V}_N \left\{ {k_i } \right\}} \\ {{ V}_N \left\{ {k_{i + 1} } \right\}} \end{array} \!\! \right] $ | (12) |
因为柔性体内相邻单元之间是完全固结的,所以其速度递推关系为
| $ { V}_E \left\{ {k_i } \right\} = { \varPhi }\left\{ {k_i ,k_{i - 1} } \right\}{ V}_E \left\{ {k_{i - 1} } \right\} + { C}\left\{ {k_i } \right\}{ \beta }\left\{ {k_i } \right\} $ | (13) |
其中
| $ \left.\!\! { \varPhi }\left\{ {k_i ,k_{i - 1} } \right\} = \left[\!\!\begin{array}{cc} {{\bf 0}_4 } & {{ I}_4 } \\ {{\bf 0}_4 } & {{\bf 0}_4 } \end{array} \!\! \right] ,\ { C}\left\{ {k_i } \right\} = \left[\!\!\begin{array}{c} {{\bf 0}_4 } \\ {{ I}_4 } \end{array}\!\! \right] \\ { \beta }\left\{ {k_i } \right\} = { V}_N \left\{ {k_{i + 1} } \right\} \right\} $ | (14) |
${ \varPhi }\left\{ {k_i ,k_{i - 1} } \right\}$为从第 $k_{i - 1}$个有限单元到第$k_i$ 个有限单元的空间算子矩阵,${ \beta }\left\{ {k_i } \right\}$为第$k_i$ 个有限单元的广义速度,${ C}\left\{ {k_i } \right\}$为第$k_i $个有限单元的广义速度向节点速度投影的映射矩阵.对式(13)进行求导,可以得到柔性体内加速度递推关系为
| $ \dot{ V}_E \left\{ {k_i } \right\} = { \varPhi }\left\{ {k_i ,k_{i - 1} } \right\}\dot{ V}_E \left\{ {k_{i - 1} } \right\} + { C}\left\{ {k_i } \right\} \dot{ \beta }\left\{ {k_i } \right\} + { c}\left\{ {k_i } \right\} $ | (15) |
其中
| $ { c}\left\{ {k_i } \right\} = \dot{ \varPhi }\left\{ {k_i ,k_{i - 1} } \right\} { V}_E \left\{ {k_{i - 1} } \right\} + \dot{ C}\left\{ {k_i } \right\} { \beta }\left\{ {k_i } \right\} $ | (16) |
考虑到在柔性体内${ \varPhi }\left\{ {k_i ,k_{i - 1} } \right\}$和$ { C}\left\{ {k_i } \right\}$为常数阵,所以${ c}\left\{ {k_i } \right\}$为0.
其次分析两个相邻柔性体之间的运动学递推关系. 第$k$个柔性体的第$k_{\left[k \right] + 1} $个节点与第$k + 1$个柔性体的第$\left( {k + 1} \right)_1 $个节点之间通过铰链连接,铰链两端的速度关系为
| $ { V}_N \left\{ {\left( {k + 1} \right)_1 } \right\} = { \chi }_{k + 1} { V}_N \left\{ {k_{\left[k \right] + 1} } \right\} + { \varepsilon }_{k + 1} { \eta }_{k + 1} $ | (17) |
其中,${ \chi }_{k + 1} $为第$k + 1$个铰链速度传递矩阵,${ \eta }_{k + 1} $为第$k + 1$个铰链的广义速度,${ \varepsilon }_{k + 1} $为第$k + 1$个铰链关节空间到节点空间的速度映射矩阵. 在平面系统中,常用的铰链为平面转动副和平面移动副,下面以这两种铰链为例进行分析.
平面转动副完全约束平动,但不约束转动,其约束关系式为
| $ { r}\left\{ {\left( {k + 1} \right)_1 } \right\} = { r}\left\{ {k_{\left[k \right] + 1} } \right\} $ | (18) |
所以
| $ { \eta }_{k + 1} = \left[\!\!\begin{array}{c} {{\dot {x}}'\left\{ {\left( {k + 1} \right)_1 } \right\}} \\ {{\dot {y}}'\left\{ {\left( {k + 1} \right)_1 } \right\}} \end{array} \!\! \right] ,\ { \chi }_{k + 1} = \left[\!\! \begin{array}{cc} {{ I}_2 } \!\! &\!\! \\ \!\! & \!\! {{\bf 0}_2 } \end{array} \!\! \right] ,\ { \varepsilon }_{k + 1} = \left[\!\!\begin{array}{c} {{\bf 0}_2 } \\ {{ I}_2 } \end{array} \!\!\right] $ | (19) |
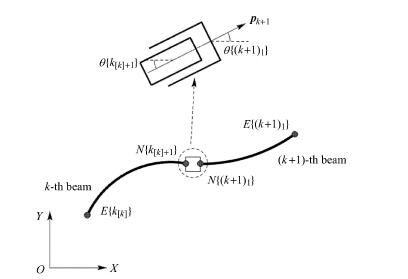
如图 4所示,平面移动副约束一个方向的平动,同时限制铰链两端转角相同.
|
图 4 平面移动副 Figure 4 The planar translational joint |
假设平面移动副的滑动方向为$ { p}_{k + 1} $,其约束方程为
| $\begin{align} & \theta \left\{ {{\left( k+1 \right)}_{1}} \right\}=\theta \left\{ {{k}_{\left[ k \right]+1}} \right\}\Rightarrow {r}'\left\{ {{\left( k+1 \right)}_{1}} \right\}={{\lambda }_{k+1}}{r}'\left\{ {{k}_{\left[ k \right]+1}} \right\} \\ & \Rightarrow {\dot{r}}'\left\{ {{\left( k+1 \right)}_{1}} \right\}={{\lambda }_{k+1}}{\dot{r}}'\left\{ {{k}_{\left[ k \right]+1}} \right\}+{{{\dot{\lambda }}}_{k+1}}{r}'\left\{ {{k}_{\left[ k \right]+1}} \right\}\dot{r}\left\{ {{\left( k+1 \right)}_{1}} \right\} \\ & =\dot{r}\left\{ {{k}_{\left[ k \right]+1}} \right\}+{{p}_{k+1}}{{{\dot{\gamma }}}_{k+1}} \\ \end{align}$ | (20) |
所以
| $ \left.\!\! { \eta }_{k + 1} = \left[\!\!\begin{array}{c} {\dot {\gamma }_{k + 1} } \\ {\dot {\lambda }_{k + 1} } \end{array}\!\! \right] ,\ { \chi }_{k + 1} = \left[\!\!\begin{array}{cc} {{ I}_2 } & {\bf 0} \\ {\bf 0} & {\lambda _{k + 1} { I }_2 } \end{array}\!\! \right]\\ { \varepsilon }_{k + 1} = \left[\!\! \begin{array}{cc} {{ p }_{k + 1} } & {\bf 0} \\ {\bf 0} & {{ r}'\left\{ {k_{\left[k \right] + 1} } \right\}} \end{array}\!\! \right] \right\} $ | (21) |
由式(17)可以得到柔性体之间单元的速度递推关系
| $ { V }_E \left\{ {\left( {k + 1} \right)_1 } \right\} = { \varPhi }\left\{ {\left( {k + 1} \right)_1 ,k_{\left[k \right]} } \right\}{ V }_E \left\{ {k_{\left[k \right]} } \right\} + \\ { C }\left\{ {\left( {k + 1} \right)_1 } \right\}{ \beta }\left\{ {\left( {k + 1} \right)_1 } \right\} $ | (22) |
其中
| $\begin{align} & \beta \left\{ {{\left( k+1 \right)}_{1}} \right\}=\left[ \begin{matrix} {{\eta }_{k+1}} \\ {{V}_{N}}\left\{ {{\left( k+1 \right)}_{2}} \right\} \\ \end{matrix} \right]\left\{ {{\left( k+1 \right)}_{1}},{{k}_{\left[ k \right]}} \right\} \\ & =\left[ \begin{matrix} {{\mathbf{0}}_{4}} & {{\chi }_{k+1}} \\ {{\mathbf{0}}_{4}} & {{\mathbf{0}}_{4}} \\ \end{matrix} \right]C\left\{ {{\left( k+1 \right)}_{1}} \right\}=\left[ \begin{matrix} {{\varepsilon }_{k+1}} & \mathbf{0} \\ \mathbf{0} & {{I}_{4}} \\ \end{matrix} \right] \\ \end{align}$ | (23) |
对式(22)进行求导,可以得到加速度递推关系
| $\begin{align} & {{{\dot{V}}}_{E}}\left\{ {{\left( k+1 \right)}_{1}} \right\}=\left\{ {{\left( k+1 \right)}_{1}},{{k}_{\left[ k \right]}} \right\}{{{\dot{V}}}_{E}}\left\{ {{k}_{\left[ k \right]}} \right\}+ \\ & C\left\{ {{\left( k+1 \right)}_{1}} \right\}\dot{\beta }\left\{ {{\left( k+1 \right)}_{1}} \right\}+c\left\{ {{\left( k+1 \right)}_{1}} \right\} \\ \end{align}$ | (24) |
其中
| $ { c}\left\{ {\left( {k + 1} \right)_1 } \right\} = \dot {\varPhi }\left\{ {\left( {k + 1} \right)_1 ,k_{\left[k \right]} } \right\}{ V}_E \left\{ {k_{\left[k \right]} } \right\} + \\ \dot { C}\left\{ {\left( {k + 1} \right)_1 } \right\}{ \beta } \left\{ {\left( {k + 1} \right)_1 } \right\} $ | (25) |
对于平面转动副,${ \varPhi }\left\{ {\left( {k + 1} \right)_1 ,k_{\left[k \right]} } \right\}$和${ C}\left\{ {\left( {k + 1} \right)_1 } \right\}$为常数阵,${ c}\left\{ {\left( {k + 1} \right)_1 } \right\}$为 0;对于平面移动副,${ \varPhi }\left\{ {\left( {k + 1} \right)_1 ,k_{\left[k \right]} } \right\}$和${ C}\left\{ {\left( {k + 1} \right)_1 } \right\}$不为常数阵,${ c}\left\{ {\left( {k + 1} \right)_1 } \right\}$不为 0.
定义系统空间算子矩阵SKO为
| $ { \varepsilon }_\varPhi = \left[\begin{array}{ccccc} {{ \varepsilon }_{\varPhi \left\{ 1 \right\}} } & & & & \\ {{ \varepsilon }_{\varPhi \left\{ {2,1} \right\}} } & { { \varepsilon }_{\varPhi \left\{ 2 \right\}} } & & {\bf 0} & \\ & {{ \varepsilon }_{\varPhi \left\{ {3,2} \right\}} } & {{ \varepsilon }_{\varPhi \left\{ 3 \right\}} } & & \\ & & \ddots & \ddots & \\ & {\bf 0} & & {{ \varepsilon }_{\varPhi \left\{ {N,N - 1} \right\}} } & {{ \varepsilon }_{\varPhi \left\{ N \right\}} } \end{array} \!\! \right] $ | (26) |
其中
| $\begin{align} & {{\varepsilon }_{\Phi \left\{ k \right\}}}=\left[ \begin{matrix} \mathbf{0} & {} & {} & {} & {} \\ \Phi \left\{ {{k}_{2}},{{k}_{1}} \right\} & 0 & {} & 0 & {} \\ {} & \Phi \left\{ {{k}_{3}},{{k}_{2}} \right\} & 0 & {} & {} \\ {} & {} & \ddots & \ddots & {} \\ \mathbf{0} & {} & {} & \Phi \left\{ {{k}_{\left[ k \right]}},{{k}_{\left[ k \right]-1}} \right\} & \mathbf{0} \\ \end{matrix} \right] \\ & {{\varepsilon }_{\Phi \left\{ k+1,k \right\}}}=\left[ \begin{matrix} {} & \mathbf{0} & {} & {} & \left\{ {{\left( k+1 \right)}_{1}},{{k}_{\left[ k \right]+1}} \right\} \\ {} & {} & {} & {} & {} \\ {} & {} & {} & {} & {} \\ {} & \mathbf{0} & {} & {} & \mathbf{0} \\ \end{matrix} \right] \\ \end{align}$ | (27) |
无论是柔性体内速度传递还是柔性体间速度传递,相邻有限单元$a,b,c$之间的空间算子${ \varPhi }_{a,b} ,{ \varPhi }_{b,c} $都满足如下形式
| $ { \varPhi }_{a,b} = \left[\!\! \begin{array}{cc} {{\bf 0}_4 } & * \\ {{\bf 0}_4 } & {{\bf 0}_4 } \end{array} \!\! \right] ,\ { \varPhi }_{b,c} = \left[\!\! \begin{array}{cc} {{\bf 0}_4 } & * \\ {{\bf 0}_4 } & {{\bf 0}_4 } \end{array} \!\! \right] $ | (28) |
所以
| $ { \varPhi }_{a,c} = { \varPhi }_{a,b} { \varPhi }_{b,c} = {\bf 0} $ | (29) |
因此系统空间算子矩阵SKO满足如下关系
| $ \left( {{ \varepsilon }_\varPhi } \right)^m = {\bf 0} ,\ m ≥ 2 $ | (30) |
定义系统空间算子矩阵SPO为
| $ { \varPhi} = \left[\!\! \begin{array}{ccccc} {{ \varPhi }_{\left\{ 1 \right\}} } & & & & \\ {{ \varPhi }_{\left\{ {2,1} \right\}} } & {{ \varPhi }_{\left\{ 2 \right\}} } & & {\bf 0} & \\ & {{ \varPhi }_{\left\{ {3,2} \right\}} } & {{ \varPhi }_{\left\{ 3 \right\}} } & & \\ & & \ddots & \ddots & \\ & {\bf 0} & & {{ \varPhi }_{\left\{ {N,N - 1} \right\}} } & {{ \varPhi }_{\left\{ N \right\}} } \end{array}\!\! \right] $ | (31) |
其中
| $\begin{align} & {{\Phi }_{\left\{ k \right\}}}=\left[ \begin{matrix} I & {} & {} & {} & {} \\ \Phi \left\{ {{k}_{2}},{{k}_{1}} \right\} & I & {} & 0 & {} \\ {} & \Phi \left\{ {{k}_{3}},{{k}_{2}} \right\} & I & {} & {} \\ {} & {} & \ddots & \ddots & {} \\ \mathbf{0} & {} & {} & \Phi \left\{ {{k}_{\left[ k \right]}},{{k}_{\left[ k \right]-1}} \right\} & I \\ \end{matrix} \right] \\ & {{\Phi }_{\left\{ k+1,k \right\}}}=\left[ \begin{matrix} {} & \mathbf{0} & {} & {} & \Phi \left\{ {{\left( k+1 \right)}_{1}},{{k}_{\left[ k \right]+1}} \right\} \\ {} & {} & {} & {} & {} \\ {} & {} & {} & {} & {} \\ {} & \mathbf{0} & {} & {} & 0 \\ \end{matrix} \right] \\ \end{align}$ | (32) |
根据式(30)和式(31),可以得到空间算子矩阵SPO满足如下关系
| $ { \varPhi } = { I } + { \varepsilon }_\varPhi = { I} + { \varepsilon }_\varPhi + \sum_{m = 2}^{ + \infty } {\left( {{ \varepsilon }_\varPhi } \right)^m} = \left( {{ I} -{ \varepsilon }_\varPhi } \right)^{ - 1} $ | (33) |
定义
| ${{V}_{E}}=\text{col}\left\{ {{V}_{E}}\left\{ k \right\} \right\},\beta =\text{col}\left\{ \beta \left\{ k \right\} \right\}C=\text{diag}\left\{ C\left\{ k \right\} \right\},c=\text{col}\left\{ c\left\{ k \right\} \right\}$ | (34) |
其中
| $\begin{align} & {{V}_{E}}\left\{ k \right\}=\text{col}\left\{ {{V}_{E}}\left\{ {{k}_{i}} \right\} \right\},\beta \left\{ k \right\}=\text{col}\left\{ \beta \left\{ {{k}_{i}} \right\} \right\} \\ & C\left\{ k \right\}=\text{diag}\left\{ C\left\{ {{k}_{i}} \right\} \right\},c\left\{ k \right\}=\text{col}\left\{ c\left\{ {{k}_{i}} \right\} \right\} \\ \end{align}$ | (35) |
结合式(13),式(15),式(22),式(24),式(26),式(33)和式(34),可以得到系统整体的运动学递推关系
| $\begin{align} & \left\{ \begin{array}{*{35}{l}} {{V}_{E}}={{\varepsilon }_{\Phi }}{{V}_{E}}+C\beta \\ {{{\dot{V}}}_{E}}={{\varepsilon }_{\Phi }}{{{\dot{V}}}_{E}}+C\dot{\beta }+c \\ \end{array} \right.\Rightarrow \left\{ \begin{array}{*{35}{l}} {{V}_{E}}={{\left( I-{{\varepsilon }_{\Phi }} \right)}^{-1}}C\beta \\ {{{\dot{V}}}_{E}}={{\left( I-{{\varepsilon }_{\Phi }} \right)}^{-1}}\left( C\dot{\beta }+c \right) \\ \end{array} \right. \\ & \Rightarrow \left\{ \begin{array}{*{35}{l}} {{V}_{E}}=\Phi C\beta \\ {{{\dot{V}}}_{E}}=\Phi \left( C\dot{\beta }+c \right) \\ \end{array} \right. \\ \end{align}$ | (36) |
根据虚功率原理
| $ { f}_{E} \cdot \delta { V}_E = { Q} \cdot \delta { \beta } $ | (37) |
其中,${ f}_E $为系统单元所受到的主动力,${ Q}$为广义力.
| ${{f}_{E}}={{M}_{E}}{{\dot{V}}_{E}}+{{F}_{EK}}-{{F}_{E}}$ | (38) |
其中,${ F}_E $为系统所受外力${ F}$所对应的单元节点力.将式(36)和式(38)代入式(37),可以得到
| $ { Q} = { C}^{\rm T}{ \varPhi }^{\rm T}{ f}_E = { C}^{\rm T}{ \varPhi }^{\rm T}\left( {{ M}_E \dot{ V}_E + { F}_{EK} - { F}_E } \right) $ | (39) |
将式(36)代入式(39),可以得到系统总动力学方程为
| $ { Q} = { \Omega} \dot {\beta } + { \Gamma } $ | (40) |
其中,${ \Omega }$为广义质量,${ \Gamma }$为广义外力.
| $ \left. { \Omega } = { C}^{\rm T}{ \varPhi }^{\rm T}{ M}_E { \varPhi C} \\ { \Gamma } = { C}^{\rm T}{ \varPhi }^{\rm T}\left( {{ M}_E { \varPhi c} + { F}_{EK} - { F}_E } \right) \right\} $ | (41) |
为了阐述方便,从基座向端部逐单元重新编号,即$1,2,\cdots ,s,\cdots,\bar {N}$,其中总单元数$\bar {N} = \sum_{k = 1}^N {\left[k\right]} $,
第$k$个柔性体的第$i$个单元所对应的单元编号为
| $ s\left\{ {k_i } \right\} = \sum_{j = 1}^{k - 1} {\left[j \right]} + i $ | (42) |
两种编号标记下,任意矢量${ X }$分量关系为
| $ { X}_s = { X}\left\{ {k_i } \right\} $ | (43) |
根据式(41),广义质量矩阵可以写成如下形式
| $\Omega ={{C}^{\text{T}}}{{\Phi }^{\text{T}}}{{M}_{E}}C=\quad \left[ \begin{matrix} {{\tau }_{1}} & \upsilon _{2,1}^{\text{T}} & {} & {} & {} \\ {} & {} & {} & {} & {} \\ {{\upsilon }_{2,1}} & {{\tau }_{2}}\upsilon _{3,2}^{\text{T}} & \mathbf{0} & {} & {} \\ {} & {{\upsilon }_{3,2}} & {{\tau }_{3}} & \ddots & {} \\ {} & {} & \ddots & \ddots & \upsilon _{\bar{N},\bar{N}-1}^{\text{T}} \\ {} & \mathbf{0} & {} & {{\upsilon }_{\bar{N},\bar{N}-1}} & {{\tau }_{{\bar{N}}}} \\ \end{matrix} \right]$ | (44) |
其中
| ${{\tau }_{s}}=C_{s}^{\text{T}}\left( {{M}_{E\left( s \right)}}+\Phi _{s+1,s}^{\text{T}}{{M}_{E\left( s+1 \right)}}{{\Phi }_{s+1,s}} \right){{C}_{s}}{{\upsilon }_{s+1,s}}=C_{s+1}^{\text{T}}{{M}_{E\left( s+1 \right)}}{{\Phi }_{s+1,s}}{{C}_{s}}$ | (45) |
令
| $\left. \matrix{ \left. \matrix{ {P_1} = {\tau _1} \hfill \cr {P_s} = {\tau _s} - {\upsilon _{s,s - 1}}P_{s - 1}^{ - 1}\upsilon _{s,s - 1}^{\rm{T}},s = 2,3, \cdots \bar N \hfill \cr} \right\} \hfill \cr \left. {\matrix{ {{\Psi _{s,s - 1}} = - {\upsilon _{s,s - 1}}P_{s - 1}^{ - 1},s = 2,3, \cdots \bar N} \hfill \cr {{\Psi _{m,n}} = \mathop {\mathop \Pi \limits^{n + 1} }\limits_{i = m} {\mkern 1mu} {\Psi _{i,i - 1}}} \hfill \cr } } \right\} \hfill \cr} \right\}$ | (46) |
则广义质量矩阵的逆可以如下分解
| $ { \Omega }^{ - 1} = { \varPsi }^{\rm T}{ P }^{ - 1} { \varPsi } $ | (47) |
其中
| $ \left. \!\! { \varPsi } = \left[\!\! \begin{array}{ccccc} { I } & & & & \\ {{ \varPsi }_{2,1} } & { I } & & {\bf 0} & \\ {{ \varPsi }_{3,1} } & {{ \varPsi }_{3,2} } & { I } & & \\ \vdots & \vdots & \ddots & \ddots & \\ {{ \varPsi }_{\bar {N},1} } & {{ \varPsi }_{\bar {N},2} } & {{ \varPsi }_{\bar {N},3} } & \cdots & { I } \end{array}\!\! \right] \\ { P } = \left[\!\! \begin{array}{ccccc} {{ P }_1 } & & & & \\ & {{ P }_2 } & & {\bf 0} & \\ & & {{ P }_3 } & & \\ & & & \ddots & \\ & {\bf 0} & & & {{ P }_{\bar N} } \end{array} \!\! \right] \!\! \right\} $ | (48) |
所以将式(47)代入式(40),动力学方程可以写成
| $\dot{\beta }={{\Omega }^{-1}}\left( Q-\Gamma \right)={{\Phi }^{\text{T}}}{{P}^{-1}}\Psi \left[ Q-{{C}^{\text{T}}}{{\Phi }^{\text{T}}}\left( {{M}_{E}}\Psi c+{{F}_{EK}}-{{F}_{E}} \right) \right]$ | (49) |
令
| $ { \gamma } = { Q} - { C}^{\rm T}{ \varPhi }^{\rm T}\left( {{ M}_E { \varPhi c} + { F}_{EK} - { F}_E } \right) $ | (50) |
其分量形式为
| $\begin{align} & \left[ \begin{matrix} {{\gamma }_{1}} \\ {{\gamma }_{2}} \\ {{\gamma }_{3}} \\ \vdots \\ {{\gamma }_{{\bar{N}}}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{Q}_{1}} \\ {{Q}_{2}} \\ {{Q}_{3}} \\ \vdots \\ {{Q}_{{\bar{N}}}} \\ \end{matrix} \right]-\left[ \begin{matrix} C_{1}^{\text{T}} & C_{1}^{\text{T}}\Phi _{2,1}^{\text{T}} & {} & {} & {} \\ {} & C_{2}^{\text{T}} & C_{2}^{\text{T}}\Phi _{3,2}^{\text{T}} & {} & \mathbf{0} \\ {} & {} & C_{3}^{\text{T}} & \ddots & {} \\ {} & {} & {} & \ddots & C_{\bar{N}-1}^{\text{T}}\Phi _{\bar{N},\bar{N}-1}^{\text{T}} \\ {} & \mathbf{0} & {} & {} & C_{{\bar{N}}}^{\text{T}} \\ \end{matrix} \right] \\ & \$\left( \left[ \begin{matrix} {{M}_{E(1)}}\left( {{c}_{1}} \right) \\ {{M}_{E(2)}}\left( \text{ }{{\Phi }_{2,1}}{{c}_{1}}+{{c}_{2}} \right) \\ {{M}_{E(3)}}\left( \text{ }{{\Phi }_{3,2}}{{c}_{2}}+{{c}_{3}} \right) \\ \vdots \\ {{M}_{E\left( {\bar{N}} \right)}}\left( \text{ }{{\Phi }_{\bar{N},\bar{N}-1}}{{c}_{\bar{N}-1}}+{{c}_{{\bar{N}}}} \right) \\ \end{matrix} \right]+\left[ \begin{matrix} {{F}_{EK(1)}}-{{F}_{E(1)}} \\ {{F}_{EK(2)}}-{{F}_{E(2)}} \\ {{F}_{EK(3)}}-{{F}_{E(3)}} \\ \vdots \\ {{F}_{EK(\bar{N})}}-{{F}_{E(\bar{N})}} \\ \end{matrix} \right] \right) \\ \end{align}$ | (51) |
所以对应的递推算法1为
| $\begin{align} & \left[ \begin{array}{*{35}{l}} \text{for}s=1,2,\cdots ,\bar{N} \\ \text{if}s=1 \\ {{\kappa }_{s}}={{M}_{E\left( s \right)}}\left( {{c}_{s}} \right)+{{F}_{EK\left( s \right)}}-{{F}_{E\left( s \right)}} \\ \text{else} \\ {{\kappa }_{s}}={{M}_{E\left( s \right)}}\left( {{\Phi }_{s,s-1}}{{c}_{s-1}}+{{c}_{s}} \right)+{{F}_{EK\left( s \right)}}-{{F}_{E\left( s \right)}} \\ \text{endloop} \\ \end{array} \right] \\ & \left[ \begin{array}{*{35}{l}} \text{for}s=\bar{N},\cdots ,2,1 \\ \text{if}s=\bar{N} \\ {{\gamma }_{s}}={{Q}_{s}}-C_{s}^{\text{T}}\left( {{\kappa }_{s}} \right) \\ \text{else} \\ {{\gamma }_{s}}={{Q}_{s}}-C_{s}^{\text{T}}\left( {{\kappa }_{s}}+\Phi _{s+1,s}^{\text{T}}{{\kappa }_{s+1}} \right) \\ \text{endloop} \\ \end{array} \right] \\ \end{align}$ | (52) |
式(49)可以写成
| $ \dot{ \beta } = \left( {{ \varPsi }^{\rm T}{ P}^{ -1}{ \varPsi }} \right){ \gamma } $ | (53) |
其分量形式为
| $\begin{align} & \$\left[ \begin{matrix} {{{\dot{\beta }}}_{1}} \\ {{{\dot{\beta }}}_{2}} \\ {{{\dot{\beta }}}_{3}} \\ \vdots \\ {{{\dot{\beta }}}_{{\bar{N}}}} \\ \end{matrix} \right]=\left[ \begin{matrix} I & \psi _{2,1}^{\text{T}} & \psi _{3,1}^{\text{T}} & \cdots & \psi _{\bar{N},1}^{\text{T}} \\ {} & I & \psi _{3,2}^{\text{T}} & \cdots & \psi _{\bar{N},2}^{\text{T}} \\ {} & {} & I & \cdots & \psi _{\bar{N},3}^{\text{T}} \\ {} & \mathbf{0} & {} & \ddots & \vdots \\ {} & {} & {} & {} & I \\ \end{matrix} \right]\text{diag}\left\{ P_{s}^{-1} \right\} \\ & \$\left[ \begin{matrix} I & {} & {} & {} & {} \\ \text{ }{{\psi }_{2,1}} & I & {} & \mathbf{0} & {} \\ {{\psi }_{3,1}} & \text{ }{{\psi }_{3,2}} & I & {} & {} \\ \vdots & \vdots & \vdots & \ddots & {} \\ \text{ }{{\psi }_{\bar{N},1}} & \text{ }{{\psi }_{\bar{N},2}} & \text{ }{{\psi }_{\bar{N},3}} & \cdots & I \\ \end{matrix} \right]\left[ \begin{matrix} {{\gamma }_{1}} \\ {{\gamma }_{2}} \\ {{\gamma }_{3}} \\ \vdots \\ {{\gamma }_{{\bar{N}}}} \\ \end{matrix} \right] \\ \end{align}$ | (54) |
所以对应的递推算法2为
| $\left[ \begin{array}{*{35}{l}} \text{for}s=1,2,\cdots ,\bar{N} \\ \text{if}s=1 \\ {{\varepsilon }_{s}}={{\gamma }_{s}} \\ \text{else} \\ {{\varepsilon }_{s}}={{\Phi }_{s,s-1}}{{\varepsilon }_{s-1}}+{{\gamma }_{s}} \\ \text{endloop} \\ \end{array} \right]\left[ \begin{array}{*{35}{l}} \text{for}s=\bar{N},\cdots ,2,1 \\ \text{if}s=\bar{N} \\ {{{\dot{\beta }}}_{s}}=P_{s}^{-1}{{\varepsilon }_{s}} \\ \text{else} \\ {{{\dot{\beta }}}_{s}}=\Phi _{s+1,s}^{\text{T}}{{{\dot{\beta }}}_{s+1}}+P_{s}^{-1}{{\varepsilon }_{s}} \\ \text{endloop} \\ \end{array} \right]$ | (55) |
RANCF的动力学递推算法由式(52)和式(55)两部分组成.
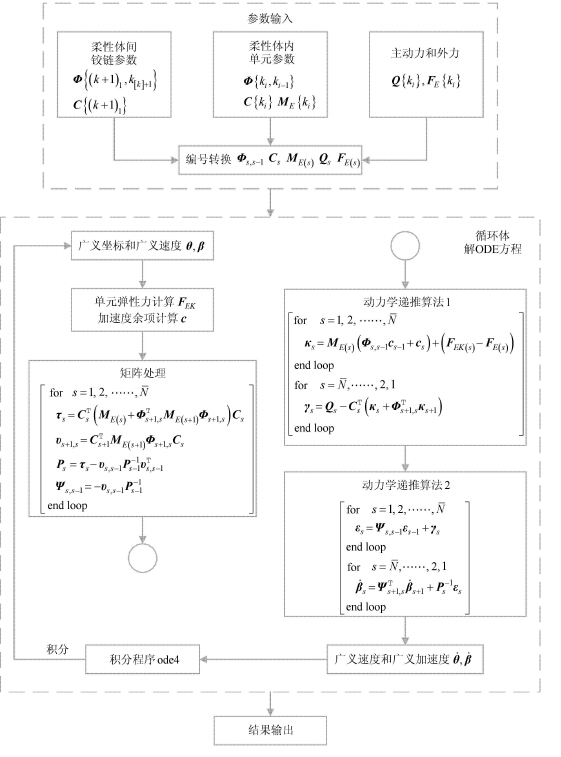
1.4 RANCF算法流程和算法复杂度分析RANCF算法流程如图 5所示,包括参数设定(输入),循环体计算和结果输出3个部分. 算法复杂度主要考虑算法中乘法的次数,下面对RANCF算法复杂度进行简单的分析.
|
图 5 RANCF 算法流程 Figure 5 The algorithm flow of RANCF |
参数输入和结果输出部分主要完成数据的输入输出,计算量很小,可以忽略.算法主体在循环体内对系统ODE形式动力学方程的求解.
对于单元弹性力的计算,根据式(7)以及参数阵${ A }_{11} ,{ A }_{12} ,{ A }_{21} ,{ A }_{22} ,{ B }_{11} ,{ B }_{12} ,{ B }_{21} ,{ B }_{22} $相互关系[4],可使其运算量小于$4\times 8^2\bar {N}$;而对于加速度余项的计算,根据式(16)和式(25),只有与平面移动副连接的单元,其加速度余项才不为0,所以计算量可忽略不计.每个块矩阵的维数均小于$8\times 8$,矩阵处理部分计算量小于$10\times 8^3\bar {N}$,动力学递推算法部分计算量小于$8\times 8^2\bar {N}$.
综上,算法总计算量小于$\left( {92\times 64} \right)\bar {N}$,对于平面转动副和平面移动副连接的系统,其自由度为
| $n=4\bar{N}+2N$ | (56) |
所以算法总计算量
| $ f\left( n \right) < \left( {92\times 64} \right)\bar {N} <147 2n \sim O\left( n \right) $ | (57) |
所以RANCF方法的计算复杂度为$O(n)$.
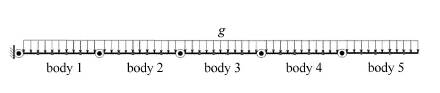
2 算例如图 6所示,平面柔性摆系统由5段柔性梁组成,每段柔性梁分成5个有限单元,单元模型采用Shabana一维两节点梁单元模型.系统初始时刻位于水平位置,在重力作用下来回摆动,其参数如表 1所示.
|
图 6 平面柔性摆系统 Figure 6 The planar flexible pendulum system |
参照文献[32]的思路,表 1中单元弹性模量为210 GPa,近似为刚体,此时MSC.ADAMS多刚体动力学的计算结果可视为准确解,以此为基准可以对RANCF方法的误差进行分析.
| 表 1 平面柔性摆系统参数表 Table 1 The parameters of the planar flexible pendulum system |
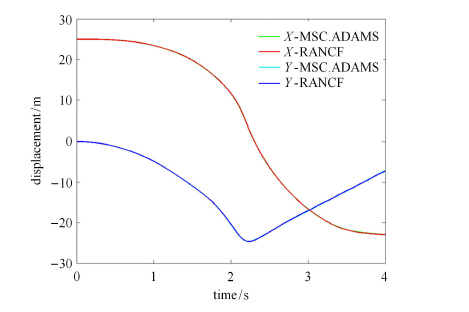
利用MSC.ADAMS软件和RANCF计算的平面柔性摆末端点的位移曲线如图 7所示,可以看出两者几乎完全吻合.
|
图 7 平面柔性摆末端点位移曲线($E = 210$ GPa) Figure 7 The displacement of the end note of the planar flexible pendulum system ($E = 210$ GPa) |
以MSC.ADAMS软件计算结果作为精确解,令系统的特征长度$L = 25$ m,则RANCF方法计算的平面柔性摆末端点位移的归一化误差为
| $ \delta _X = \Delta X / L\times 100% ,\ \delta _Y = \Delta Y / L\times 100% $ | (58) |
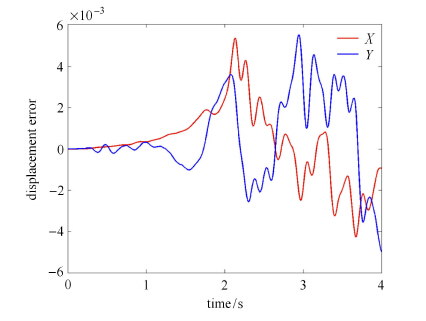
如图 8所示,RANCF的归一化误差在0.6%以内,证明了其精确性符合实际要求.
|
图 8 平面柔性摆末端点位移误差曲线($E = 210$ GPa) Figure 8 The displacement error of the end note of the planar flexible pendulum system ($E = 210$ GPa) |
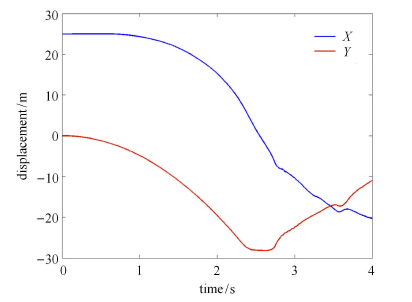
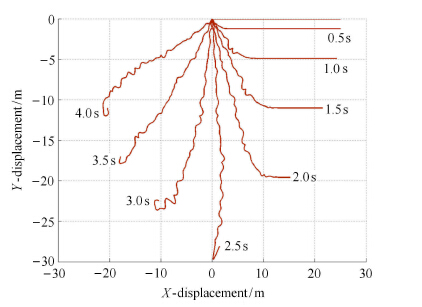
在表 1其余参数不变的情况下,将弹性模量改为21 MPa,此时系统变为非线性大变形多体系统.令仿真步长0.001 s,仿真时间4 s,利用RANCF计算的平面柔性摆末端点的位移曲线如图 9所示.图 10显示了平面柔性摆在不同时刻下的位型(每个单元的位型曲线用11个点差值近似),可以看出当弹性模量为21 MPa时,系统存在显著的柔性大变形现象.
|
图 9 平面柔性摆末端点位移曲线($E = 21$ MPa) Figure 9 The displacement of the end note of the planar flexible pendulum system($E = 21$ MPa) |
|
图 10 $t = 0.5$ s,1.0 s,1.5 s,2.0 s,2.5 s,3.0 s,3.5 s,4.0 s时刻平面柔性摆($E = 21$ MPa) Figure 10 The planar flexible pendulum at the time $t = 0.5$ s,1.0 s,1.5 s,2.0 s,2.5 s,3.0 s,3.5 s,4.0 s |
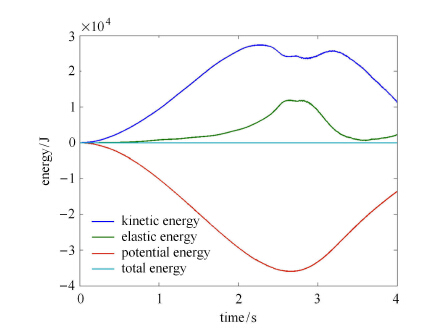
图 11显示了系统的动能、弹性能、势能和总能量曲线,其中总能量波动在0.1 J量级,相比于动能、弹性能、势能的10$^{4}$J 量级,其相对误差在0.01%,符合能量守恒定律,进一步证明了RANCF方法的准确性.
|
图 11 中平面柔性摆系统能量曲线($E = 21$ MPa)文标题 Figure 11 The Energy curve of the planar flexible pendulum system ($E = 21$ MPa) |
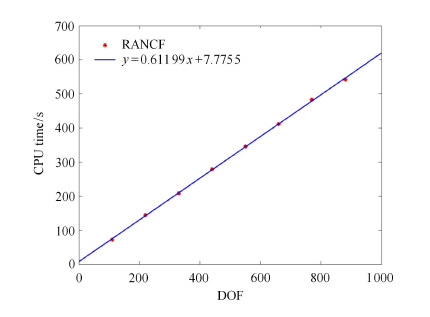
在系统其余参数不变的情况下,增加柔性梁个数,系统自由度DOF也相应增加. 计算机处理器为Inter Core i7-5500U@2.40 GHz双核,内存为16 GB,采用MATLAB仿真. 图 12显示了在DOF为110,220,330,440,550,660,770, 880时,RANCF的CPU计算时间. 为了保证数据的可靠性,CPU计算时间采用3次计算的平均值.对数据进行拟合,可以看出RANCF的DOF-CPU时间曲线符合线性关系,进而验证了RANCF计算复杂度为$O(n)$.
|
图 12 RANCF的CPU计算时间曲线 Figure 12 The DOF-CPU time curve of the RANCF |
本文针对传统绝对节点坐标法(ANCF)计算效率低的问题,提出了一种算法复杂度为$O(n)$的递推绝对节点坐标法(RANCF). 该方法借鉴Featherstone铰接体递推算法思路建立多柔体系统逐单元的运动学和动力学递推关系,在得到的ODE方程中,系统广义质量阵为三对角块矩阵,通过恰当的矩阵处理,可以逐单元递推求解该方程,从而实现$O(n)$的算法复杂度. RANCF方法保留了ANCF对大转动、大变形多柔体系统精确计算的优点,同时极大的提升了算法效率. 并且该方法采用ODE求解,无DAE的违约问题,因此具有更高的算法精度. 在算例部分,利用5梁25单元的平面柔性摆系统进行验证,通过小变形(E=210 GPa)情况下与MSC.ADAMS软件的对比,以及大变形(E=21 MPa)情况下能量指标校核,证明RANCF的精确性. 通过DOF-CPU计算时间曲线进一步验证了RANCF的算法复杂度为$O(n)$. 通过引入拓扑结构,可使RANCF适用于所有的柔性多体系统,后续工作将对RANCF进行进一步完善.
| 1 |
Likins PW. Finite element appendage equations for hybrid coordinate dynamic analysis.
International Journal of Solids and Structures,1972, 8 (5) : 709-731.
DOI: 10.1016/0020-7683(72)90038-8. ( 0) 0)
|
| 2 |
洪嘉振.
计算多体系统动力学. 北京: 高等教育出版社, 2003 .
( Hong Jiazhen.
Computational Multibody Dynamics. Beijing: Higher Education Press, 2003 .
(in Chinese) ) ( 0) 0)
|
| 3 |
陈思佳, 章定国, 洪嘉振. 大变形旋转柔性梁的一种高次刚柔耦合动力学模型.
力学学报,2013, 45 (2) : 251-256.
( Chen Sijia, Zhang Dingguo, Hong Jiazhen. A high-order rigid-flexible coupling model of a rotating flexible beam under large deformation.
Chinese Journal of Theoretical and Applied Mechanics,2013, 45 (2) : 251-256.
(in Chinese) ) ( 0) 0)
|
| 4 |
Shabana AA. An absolute nodal coordinate formulation for the large rotation and deformation analysis of flexible bodies. Department of Mechanical and Industrial Engineering, University of Illinois at Chicago, 1996
( 0) 0)
|
| 5 |
Escalona JL, Hussien HA, Shabana AA. Application of the absolute nodal coordinate formulation to multibody system dynamics. Department of Mechanical and Industrial Engineering, University of Illinois at Chicago, 1997
( 0) 0)
|
| 6 |
Eberhard P, Schiehlen W. Computational dynamics of multibody systems history, formalisms, and applications.
ASME Journal of Computational and Nonlinear Dynamics,2006, 1 : 3-12.
DOI: 10.1115/1.1961875. ( 0) 0)
|
| 7 |
张雄, 王天舒.
计算动力学. 2007 .
( Zhang Xiong, Wang Tianshu.
Computational Dynamics. Beijing: Tsinghua University Press, 2007 .
(in Chinese) ) ( 0) 0)
|
| 8 |
马秀腾, 翟彦博, 罗书强. 多体动力学超定运动方程广义-求解新算法.
力学学报,2012, 44 (5) : 948-52.
( Ma Xiuteng, Zhai Yanbo, Luo Shuiqiang. New generalized-method for over-determined motion equations in multibody dynamics.
Chinese Journal of Theoretical and Applied Mechanics,2012, 44 (5) : 948-52.
(in Chinese) ) ( 0) 0)
|
| 9 |
Shabana AA. Computer implementation of the absolute nodal coordinate formulation for flexible multibody dynamics.
Nonlinear Dynamics,1998, 16 (3) : 293-306.
DOI: 10.1023/A:1008072517368. ( 0) 0)
|
| 10 |
Yakoub R, Shabana A. Use of Cholesky coordinates and the absolute nodal coordinate formulation in the computer simulation of flexible multibody systems.
Nonlinear Dynamics,1999, 20 (3) : 267-282.
DOI: 10.1023/A:1008323106689. ( 0) 0)
|
| 11 |
García-Vallejo D, Mayo J, Escalona J, et al. Effcient evaluation of the elastic forces and the Jacobian in the absolute nodal coordinate formulation.
Nonlinear Dynamics,2004, 35 (4) : 313-329.
DOI: 10.1023/B:NODY.0000027747.41604.20. ( 0) 0)
|
| 12 |
Hussein B, Negrut D, Shabana AA. Implicit and explicit integration in the solution of the absolute nodal coordinate differential/algebraic equations.
Nonlinear Dynamics,2008, 54 (4) : 283-296.
DOI: 10.1007/s11071-007-9328-9. ( 0) 0)
|
| 13 |
Tian Q, Chen LP, Zhang YQ, et al. An effcient hybrid method for multibody dynamics simulation based on absolute nodal coordinate formulation.
Journal of Computational and Nonlinear Dynamics,2009, 4 (2) : 021009.
DOI: 10.1115/1.3079783. ( 0) 0)
|
| 14 |
刘铖, 田强, 胡海岩. 基于绝对节点坐标的多柔体系统动力学高效计算方法.
力学学报,2010, 42 (6) : 1197-1205.
( Liu Cheng, Tian Qiang, Hu Haiyan. Effcient computational method for dynamics of flexible multibody system based on absolute nodal coordinate.
Chinese Journal of Theoretical and Applied Mechanics,2010, 42 (6) : 1197-1205.
(in Chinese) ) ( 0) 0)
|
| 15 |
Ren H. A simple absolute nodal coordinate formulation for thin beams with large deformations and large rotations.
Journal of Computational and Nonlinear Dynamics,2015, 10 (6) : 061005.
DOI: 10.1115/1.4028610. ( 0) 0)
|
| 16 |
Hara K. A formulation of a thin plate element based on the absolute nodal coordinate formulation with artificial constraints. In:ECCOMAS Thematic Conference on Multibody Dynamics, Barcelona, Catalonia Spain. 2015
( 0) 0)
|
| 17 |
章孝顺, 章定国, 陈思佳, 等. 基于绝对节点坐标法的大变形柔性梁几种动力学模型研究.
物理学报,2016, 65 (9) : 094501.
( Zhang Xiaoshun, Zhang Dingguo, Chen Sijia, et al. Several dynamic models of a large deformation flexible beam based on the absolute nodal coordinate formulation.
Acta Phys Sin,2016, 65 (9) : 094501.
(in Chinese) ) ( 0) 0)
|
| 18 |
孔伟顺, 田强. 基于绝对节点坐标法的多体系统动力学仿真软件开发. 见:北京力学会第二十二届学术年会论文集, 北京力学会第二十二届学术年会, 北京, 2016
( Kong Weishun, Tian Qiang. The multi-system dynamics software development based on the absolute nodal coordinate formulation. In:The Twenty-Second Academic Annual Conference of the Beijing Mechanical Association, Beijing,2016(in Chinese)
) ( 0) 0)
|
| 19 |
马超, 魏承, 赵阳, 等. 绝对节点坐标列式实体梁单元建模方法及应用.
航空学报,2015, 36 (10) : 3316-3326.
( Ma Chao, Wei Cheng, Zhao Yang, et al. Modelling method and application of solid beam element based on absolute nodal coordinate formulation.
Acta Aeronautica et Astronautica Sinica,2015, 36 (10) : 3316-3326.
(in Chinese) ) ( 0) 0)
|
| 20 |
Luo K, Liu C, Tian Q, et al. Nonlinear static and dynamic analysis of hyper-elastic thin shells via the absolute nodal coordinate formulation.
Nonlinear Dynamics,2016 : 1-23.
( 0) 0)
|
| 21 |
Hyldahl P, Andersen S, Mikkelsen S, et al. Modeling and feasibility study of nonlinear suspension components in multibody systems using absolute nodal coordinate formulation based beam elementsapplication to stabilizer bar.
Human Factors,2015 : 4-14.
( 0) 0)
|
| 22 |
胡权, 贾英宏, 徐世杰. 多体系统动力学Kane方法的改进.
力学学报,2011, 43 (5) : 968-972.
( Hu Quan, Jia Yinghong, Xu Shijie. An improved Kane's method for multibody dynamics.
Chinese Journal of Theoretical and Applied Mechanics,2011, 43 (5) : 968-972.
(in Chinese) ) ( 0) 0)
|
| 23 |
梅凤翔, 吴惠彬, 李彦敏, 等. Birkho力学的研究进展.
力学学报,2016, 48 (2) : 263-268.
( Mei Fengxiang, Wu Huibin, Li Yanmin, et al. Advances in research on Birkho mechanics.
Chinese Journal of Theoretical and Applied Mechanics,2016, 48 (2) : 263-268.
(in Chinese) ) ( 0) 0)
|
| 24 |
刘菲, 胡权, 张景瑞. 树形多体系统动力学约束力算法.
力学学报,2016, 48 (1) : 201-212.
( Liu Fei, Hu Quan, Zhang Jingrui. Constraint force algorithm for tree-like multibody system dynamics.
Chinese Journal of Theoretical and Applied Mechanics,2016, 48 (1) : 201-212.
(in Chinese) ) ( 0) 0)
|
| 25 |
Featherstone R. The calculation of robot dynamics using articulatedbody inertias.
The International Journal of Robotics Research,1983, 2 (1) : 13-30.
DOI: 10.1177/027836498300200102. ( 0) 0)
|
| 26 |
Featherstone R.
Robot Dynamics Algorithm. Norwell: Kluwer Academic Publishers, 1987 .
( 0) 0)
|
| 27 |
Rodriguez G. Kalman filtering, smoothing, and recursive robot arm forward and inverse dynamics.
IEEE Journal of Robotics and Automation,1987, 3 (6) : 624-639.
DOI: 10.1109/JRA.1987.1087147. ( 0) 0)
|
| 28 |
Rodriguez G, Abhinandan J. Kreutz-Delgado K. Spatial operator algebra for multibody system dynamics.
Journal of the Astronautical Sciences,1992, 40 (1) : 27-50.
( 0) 0)
|
| 29 |
Jain A, Rodriguez G. Recursive flexible multibody system dynamics using spatial operators.
Journal of Guidance, Control, and Dynamics,1992, 15 (6) : 1453-1466.
DOI: 10.2514/3.11409. ( 0) 0)
|
| 30 |
Jain A, Rodriguez G. An analysis of the kinematics and dynamics of underactuated manipulators.
IEEE Transactions on Robotics and Automation,1993, 9 (4) : 411-422.
DOI: 10.1109/70.246052. ( 0) 0)
|
| 31 |
Omar M. Multibody dynamics formulation for modeling and simulation of roller chain using spatial operator.
In MATEC Web of Conferences, EDP Sciences,2016, 51 : 01003.
DOI: 10.1051/matecconf/20165101003. ( 0) 0)
|
| 32 |
田强. 基于绝对节点坐标方法的柔性多体系统动力学研究与应用.[博士论文]. 武汉:华中科技大学, 2009
( Tian Qiang. Flexible multibody dynamics research and application based on the absolute nodal coordinate method.[PhD Thesis]. Wuhan:Huazhong University of Science & Technology, 2009(in Chinese)
) ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48
