2. 北京信息科技大学机电工程学院, 北京 100192
随着人类对太空探索的不断深入,自由漂浮空间机器人在空间任务中发挥着越来越重要的作用,如故障卫星的在轨捕获、在轨空间站装配和维修、太空垃圾清理和空间环境下的科学实验等.空间机器人的路径优化是完成这些复杂空间任务的基础,也是实现空间任务成败的关键.由于空间机器人不具有固定基座,机械臂和载体之间存在非完整约束,使得自由漂浮空间机器人路径规划完全不同于地面机器人而变得具有挑战性.这一方面给路径规划带来一定的困难,另一方面也为控制航天器载体姿态提供了一种方法,即通过机械臂关节的运动使系统或载体的姿态达到期望的目标姿态.Dubowsky等[1]首先提出了利用关节角的周期运动改变载体姿态的思想.Krishman等[2]研究了通过机械臂的运动,调节载体姿态的最优控制问题.Yamada等[3]提出了基于操作臂沿一闭合路径运动来实现载体姿态的变化的反馈控制方法.Nakamura等[4]利用Lyapunov方法提出了一种驱动机械臂关节来同时控制载体姿态和机械臂关节角的非完整约束"双向"控制方法.刘延柱等[5]改进了文献[4]的方法,提出空间机械臂在臂端负载位形空间内的非完整运动路径规划问题.Coverstone等[6]和Cerven等[7]利用平均方法通过机械臂关节铰运动调整航天器载体最优定向.Fenandes等[8]基于泛函分析中的Ritz近似理论建立了非完整运动规划的控制方法,并求解了空间机械臂系统的优化输入和航天器姿态运动轨线.Rui等[9]研究了多体航天器通过内运动的形状改变调控航天器的姿态定位.王景等[10]对双臂自由漂浮空间机器人系统提出了利用内部运动的机器人本体姿态控制算法.赵晓东等[11]对空间机器人抓取运动目标体的问题,提出了基于轨迹规划的空间机器人优化方法.笔者[12-13]利用遗传算法和粒子群优化方法研究了航天器太阳帆板展开过程和空间机械臂的姿态最优控制问题.
近年来,伪谱法已经成为求解最优控制问题的重要方法之一[14-16],其基本原理是在正交配点处将连续最优控制问题离散化,并通过全局插值多项式逼近状态和控制变量,从而将最优控制问题(OCP)转化为非线性规划问题(NLP)求解.Elnagar等[14]首次将伪谱法转化理论应用于动态系统的最优控制,证明了该方法可以有效地将最优控制问题转化为非线性规划问题.Fahroo和Ross[15-16]基于Legendre伪谱法提出了最优控制问题转化为非线性规划问题满足的协态映射定理,即非线性规划问题的一阶必要条件KKT(Karush-Kuhn-Tucker)与最优控制所诱导的最优必要条件是等价的,实现了直接法与间接法联系和统一,奠定了伪谱法求解最优控制问题的理论基础. Rao等[17]采用Legendre伪谱法研究了再入机动飞行器的轨迹优化问题.Huntington等[18]采用Gauss伪谱法对航天器编队的轨迹优化问题进行了研究,以最小燃料消耗为性能指标,规划了航天器编队的最优轨道.雍恩米等[19]采用Gauss伪谱法求解了高超声速飞行器滑翔式再入的快速轨迹优化问题,提出了轨迹分段的优化策略.Li等[20-21]基于Gauss伪谱法求解了自由漂浮空间机器人路径优化问题,针对时间、燃料和对基座扰动最小的任务目标,得到空间机器人从初始位姿到目标位姿的最优路径.廖一寰等[22-23]结合Gauss伪谱法的计算效率以及直接打靶法的精确性,提出了空间机械臂一类混合规划策略, 分别求解了全程振动最小化与残余振动最小化的运动规划问题.
本文基于Legendre 伪谱法研究自由漂浮空间机器人最小能量的路径规划最优控制问题.首先,建立空间机器人系统的动力学方程,结合空间机器人非完整性质,选取机械臂关节耗散能最小为性能指标,并考虑实际控制输入受限,规划空间机器人从初始位形到目标位形的关节运动轨迹的最优控制问题.然后利用Legendre伪谱法,将状态变量和控制变量在Legendre-Gauss-Lobatto(LGL)点上离散,并以离散点为节点构造Lagrange插值多项式逼近系统状态和控制变量,通过对全局插值多项式求导来近似状态变量对时间的导数,将微分方程约束转换为一组代数约束,从而将连续最优控制问题转化为离散的非线性规划问题进行求解. 文末给出相应的仿真算例.
1 空间机器人动力学方程
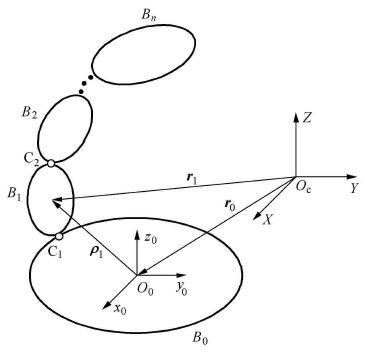
设空间机器人系统由航天器载体B0和机械臂
|
图 1 空间机械臂示意图 Fig.1 Space manipulator sketch |
| ${{r}_{i}}={{r}_{0}}+\sum\limits_{i=1}^{i}{{{\rho }_{i}}},\quad i=1,2,\cdots ,n$ | (1) |
| ${{\Omega }_{j}}={{\Omega }_{0}}+\sum\limits_{i=1}^{j}{{{\Omega }_{i-1,i}}},\quad j=1,2,\cdots ,n$ | (2) |
式中
|
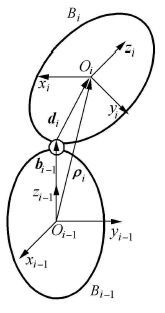
图 2 邻接刚体示意图 Fig.2 Sketch of contiguous bodies |
| ${{\rho }_{i}}={{b}_{i-1}}+{{d}_{i}}$ | (3) |
其中
| ${{m}_{0}}{{r}_{0}}+\sum\limits_{i=1}^{n}{{{m}_{i}}}{{r}_{i}}=\mathbf{0}$ | (4) |
其中m0 为载体 B0的质量,mi 为机械臂各刚体
| ${{r}_{0}}=-\frac{1}{m}\sum\limits_{i=1}^{n}{{{m}_{i}}}\sum\limits_{j=1}^{i}{{{\rho }_{j}}}=-\frac{1}{m}\sum\limits_{j=1}^{n}{(}\sum\limits_{i=j}^{n}{{{m}_{i}}}){{\rho }_{j}}$ | (5) |
式中,m为系统的总质量. 空间机器人系统相对质心
| ${{H}_{c}}={{I}_{0}}{{\Omega }_{0}}+{{m}_{0}}{{\tilde{r}}_{0}}{{\dot{r}}_{0}}+\sum\limits_{i=1}^{n}{{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{I}}}_{i}}}{{\Omega }_{\text{c},i}}+\sum\limits_{i=1}^{n}{{{m}_{i}}}{{\tilde{r}}_{i}}{{\dot{r}}_{i}}$ | (6) |
其中,符号"∼"表示矢径的反对称投影方阵,I0 为载体B0在其连体基的转动惯量,
| ${{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{I}}_{i}}={{R}_{0,i}}{{I}_{i}}R_{0,i}^{\text{T}}$ | (7) |
式中,
| ${{r}_{0}}=-\frac{1}{m}\sum\limits_{j=1}^{n}{\left[ (\sum\limits_{i=j}^{n}{{{m}_{i}}})({{R}_{0,i-1}}{{b}_{i-1}}+{{R}_{0,i}}{{d}_{i}}) \right]}$ | (8) |
式(8)对时间求导,并利用式(2)和关系式
| $\begin{align} & {{{\dot{r}}}_{0}}=\frac{1}{m}\sum\limits_{j=1}^{n}{\left[ (\sum\limits_{i=j}^{n}{{{m}_{i}}})({{R}_{0,i-1}}{{{\tilde{b}}}_{i-1}}R_{0,i-1}^{\text{T}}+{{R}_{0,i}}{{{\tilde{d}}}_{i}}R_{0,i}^{\text{T}}) \right]}{{\Omega }_{0}}+ \\ & \frac{1}{m}\sum\limits_{j=1}^{n-1}{\left[ \sum\limits_{j=k}^{n-1}{(}\sum\limits_{i=k+1}^{n}{{{m}_{i}}}){{R}_{0,i}}{{{\tilde{b}}}_{i}}R_{0,i}^{\text{T}} \right.}+ \\ & \left. \sum\limits_{j=k}^{n}{(}\sum\limits_{i=k}^{n}{{{m}_{i}}}){{R}_{0,i}}{{{\tilde{d}}}_{i}}R_{0,i}^{\text{T}} \right]{{\Omega }_{j-1,j}}+ \\ & \frac{1}{m}{{m}_{n}}{{R}_{0,m}}{{{\tilde{d}}}_{m}}R_{0,m}^{\text{T}}{{\Omega }_{n-1,n}} \\ \end{align}$ | (9) |
将式(3)代入式(1)并对时间求导,得到
| $\begin{align} & {{{\dot{r}}}_{i}}={{{\dot{r}}}_{0}}-\sum\limits_{j=1}^{n}{({{R}_{0,i-1}}{{{\tilde{b}}}_{i-1}}R_{0,i-1}^{\text{T}}+{{R}_{0,i}}{{{\tilde{d}}}_{i}}R_{0,i}^{\text{T}}}){{\Omega }_{0}}- \\ & \sum\limits_{j=1}^{n-1}{\left[ \sum\limits_{i=j}^{n-1}{{{R}_{0,i-1}}{{{\tilde{b}}}_{i-1}}R_{0,i-1}^{\text{T}}+\sum\limits_{i=j}^{n}{{{R}_{0,i}}{{{\tilde{d}}}_{i}}R_{0,i}^{\text{T}}}} \right]}{{\Omega }_{j-1,j}} \\ & -{{R}_{0,i}}{{{\tilde{d}}}_{i}}R_{0,i}^{\text{T}}{{\Omega }_{i-1,i}} \\ \end{align}$ | (10) |
将式(1)、 式(5)、 式(9)和式(10)代入式(6),可写为如下形式
| ${{H}_{\text{c}}}={{J}_{0}}{{\Omega }_{0}}+\sum\limits_{i=1}^{n}{{{J}_{i}}}{{\Omega }_{i-1,i}}$ | (11) |
其中
| $\begin{align} & {{J}_{0}}={{I}_{0}}+\sum\limits_{j=1}^{n}{{{R}_{0,j}}{{I}_{j}}R_{0,j}^{\text{T}}+\frac{1}{m}({{m}_{0}}{{{\tilde{r}}}_{0}}+\sum\limits_{i=1}^{n}{{{m}_{i}}}{{{\tilde{r}}}_{i}})}\times \\ & \sum\limits_{k=1}^{n}{\left[ (\sum\limits_{i=k}^{n}{{{m}_{i}}})({{R}_{0,k-1}}{{{\tilde{b}}}_{k-1}}R_{0,k-1}^{\text{T}}+{{R}_{0,k}}{{{\tilde{d}}}_{k}}R_{0,k}^{\text{T}}) \right]}+ \\ & \sum\limits_{k=1}^{n}{\left[ (\sum\limits_{i=k}^{n}{{{m}_{i}}}{{{\tilde{r}}}_{i}})({{R}_{0,k-1}}{{{\tilde{b}}}_{k-1}}R_{0,k-1}^{\text{T}}+{{R}_{0,k}}{{{\tilde{d}}}_{k}}R_{0,k}^{\text{T}}) \right]} \\ \end{align}$ | (12) |
| $\begin{align} & {{J}_{i}}=\left\{ \sum\limits_{j=1}^{n}{{{R}_{0,j}}}{{I}_{j}}R_{0,j}^{\text{T}}+\frac{1}{m}({{m}_{0}}{{{\tilde{r}}}_{0}}+\sum\limits_{i=1}^{n}{{{m}_{i}}}{{{\tilde{r}}}_{i}}) \right.\times \\ & \left[ \sum\limits_{k=1}^{n-1}{(}\sum\limits_{i=k-1}^{n}{{{m}_{i}}}){{R}_{0,k}}{{{\tilde{b}}}_{k}}R_{0,k}^{\text{T}} \right.+ \\ & \sum\limits_{k=1}^{n}{(}\sum\limits_{i=k}^{n}{{{m}_{i}}}){{R}_{0,k}}{{{\tilde{d}}}_{k}}R_{0,k}^{\text{T}}- \\ & \left. \sum\limits_{k=1}^{n-1}{(}\sum\limits_{i=k-1}^{n}{{{m}_{i}}}{{{\tilde{r}}}_{i}}){{R}_{0,k}}{{{\tilde{b}}}_{k}}R_{0,k}^{\text{T}} \right]- \\ & \left. \sum\limits_{k=1}^{n}{(}\sum\limits_{i=k}^{n}{{{m}_{i}}}{{{\tilde{r}}}_{i}}){{R}_{0,k}}{{{\tilde{d}}}_{k}}R_{0,k}^{\text{T}} \right\}{{R}_{0,k}}, \\ & i=1,2,\cdots ,n-1 \\ \end{align}$ | (13) |
| $\begin{align} & {{J}_{n}}=[{{R}_{0,n}}{{I}_{n}}R_{0,n}^{\text{T}}+\frac{1}{m}({{m}_{0}}{{{\tilde{r}}}_{0}}+\sum\limits_{i=1}^{n}{{{m}_{i}}}{{{\tilde{r}}}_{i}})\times \\ & {{m}_{n}}{{R}_{0,n}}{{{\tilde{d}}}_{n}}R_{0,n}^{\text{T}}-{{m}_{n}}{{{\tilde{r}}}_{n}}{{R}_{0,n}}{{{\tilde{d}}}_{n}}R_{0,n}^{\text{T}}]{{R}_{0,n}} \\ \end{align}$ | (14) |
若系统为无外力矩作用状态,设系统初始动量矩
| ${{\Omega }_{0}}=-J_{0}^{-1}\sum\limits_{i=1}^{n}{{{J}_{i}}}{{\Omega }_{i-1,i}}$ | (15) |
设机械臂各关节铰均为圆柱铰联接,令
| ${{\Omega }_{i-1,i}}={{e}_{i}}{{\dot{\theta }}_{i}}$ | (16) |
引入Cayley参数[25],航天器载体 B0 相对系统质心
| ${{\Omega }_{0}}=\frac{1}{1+{{a}^{2}}}\left[ \begin{matrix} 1 & {{a}_{3}} & -{{a}_{2}} \\ -{{a}_{3}} & 1 & {{a}_{1}} \\ {{a}_{2}} & -{{a}_{1}} & 1 \\ \end{matrix} \right]\dot{a}=\Gamma \dot{a}$ | (17) |
式中
| $\dot{a}=-{{\Gamma }^{-1}}J_{0}^{-1}\sum\limits_{i=1}^{n}{{{J}_{i}}}{{e}_{i}}{{\dot{\theta }}_{i}}$ | (18) |
式(18)为空间机器人系统的动力学非完整约束方程,机械臂的运动可产生对载体姿态的扰动.设空间机器人系统广义坐标为
| $\dot{x}=\left[ \begin{matrix} E \\ B \\ \end{matrix} \right]u=G(x)u$ | (19) |
其中E为
自由漂浮空间机器人系统路径优化问题是在指定时间内按照某一性能指标,求解从初始位姿到目标位姿的最优或近似最优的路径,同时满足某些固有的状态约束或控制受限.因此,可将上述问题转化Bolza型最优控制问题[26],即描述为:求解最优控制律u(t),确定系统从一个状态转移至另一状态过程中使得Bolza性能泛函J取最小值
| $J=\phi (x({{t}_{f}}),\ {{t}_{f}})+\int_{{{t}_{0}}}^{{{t}_{f}}}{G(x(t),\ u(t),\ t)}dt$ | (20) |
动力学方程
| $\dot{x}(t)=f(x(t),u(t),\ t)$ | (21) |
边界条件
| $\varphi (x({{t}_{0}}),\ x({{t}_{f}}),\ {{t}_{0}},\ {{t}_{f}})=0$ | (22) |
不等式路径约束
| $C(x(t),\ u(t),\ t)\le \mathbf{0}$ | (23) |
其中,
针对空间机器人系统给定的初末端姿态,选取空间机器人的机械臂关节耗散能最小为优化性能指标,根据最小能量控制原理,相应的性能指标函数可表示为[13]
| $J(u,\ t)=\int_{{{t}_{0}}}^{{{t}_{f}}}{\langle u(}t),\ u(t)\rangle dt$ | (24) |
在实际工程应用中,空间机器人系统执行机构的控制输出是有界的,因此,在设计最优控制算法的同时,还应考虑控制输入受限的情况,即将其转化为如下不等式约束
| $\left| {{u}_{i}}(t) \right|<{{u}_{m}},i=1,2,\cdots ,n$ | (25) |
其中
| $x({{t}_{0}})={{x}_{0}},x({{t}_{f}})={{x}_{f}}$ | (26) |
Legendre伪谱法属于一类典型的直接法,该方法使用正交多项式的根为配点,采用全局插值多项式作为有限基,将状态和控制变量在LGL点离散,通过Lagrange插值多项式逼近状态和控制变量,得到节点上的离散动力学方程.从而将状态方程的微分运算和性能函数中的积分运算转化为代数运算,最终将OCP转化为以节点处的状态、控制变量为待优化参量的NLP.
最优控制问题的时间取值范围为
| $t=\frac{{{t}_{f}}+{{t}_{0}}}{2}-\frac{{{t}_{0}}-{{t}_{f}}}{2}\tau $ | (27) |
在区间
| ${{L}_{N}}(\tau )=\frac{1}{{{2}^{N}}N!}\frac{{{d}^{N}}}{d{{x}^{N}}}{{({{\tau }^{2}}-1)}^{N}}$ | (28) |
这里
| ${{\Phi }_{i}}(\tau )=\frac{1}{N(N+1){{L}_{N}}({{\tau }_{i}})}\frac{({{\tau }^{2}}-1){{{\dot{L}}}_{N}}({{\tau }_{i}})}{\tau -{{\tau }_{i}}}$ | (29) |
式中
| $x(\tau )\approx X(\tau )=\sum\limits_{i=0}^{N}{{{\Phi }_{i}}(\tau ){{X}_{i}}}$ | (30) |
| $u(\tau )\approx U(\tau )=\sum\limits_{i=0}^{N}{{{\Phi }_{i}}(\tau ){{U}_{i}}}$ | (31) |
将状态变量通过插值多项式参数化后,对状态方程的微分运算可以近似为插值基函数的微分运算,则状态变量
| $\dot{x}({{\tau }_{k}})\approx {{\dot{X}}_{k}}=\sum\limits_{i=0}^{N}{{{{\dot{L}}}_{i}}({{\tau }_{k}}){{X}_{i}}}=\sum\limits_{i=0}^{N}{{{D}_{ki}}{{X}_{i}}}$ | (32) |
其中
| ${{D}_{ki}}=\left\{ \begin{array}{*{35}{l}} \frac{{{L}_{N}}({{\tau }_{k}})}{{{L}_{N}}({{\tau }_{j}})}\cdot \frac{1}{{{\tau }_{k}}-{{\tau }_{j}}}, & k\ne j \\ -\frac{N(N+1)}{4}, & k=j=0 \\ \frac{N(N+1)}{4}, & k=j=N \\ 0, & \text{other} \\ \end{array} \right.$ | (33) |
由此可将状态方程约束转化为$N + 1$组LGL配点处的离散的状态方程,有
| $\sum\limits_{i=0}^{N}{{{D}_{ki}}{{X}_{i}}}-\frac{{{t}_{f}}-{{t}_{0}}}{2}f({{X}_{k}},\ {{U}_{k}},\ {{\tau }_{k}})=\mathbf{0}$ | (34) |
离散后的边界约束及路径约束可描述为
| $\varphi ({{X}_{0}},\ {{X}_{N}},\ {{\tau }_{0}},\ {{\tau }_{N}})=0$ | (35) |
| $C({{X}_{k}},\ {{U}_{k}},\ {{\tau }_{k}})\le \mathbf{0}$ | (36) |
式中
| $J=\phi +\frac{{{t}_{f}}-{{t}_{0}}}{2}\sum\limits_{i=0}^{N}{{{w}_{i}}G({{X}_{i}},\ {{U}_{i}},\ {{\tau }_{i}})}$ | (37) |
其中
| ${{w}_{i}}=\int_{-1}^{1}{{{\Phi }_{i}}(\tau )d\tau =}\frac{2}{N(N+1)}{{\left[ {{L}_{N}}\left( {{\tau }_{i}} \right) \right]}^{-2}}$ | (38) |
通过上述离散和拟合处理,最优控制问题式(20) ∼式(23)可进一步描述为:求解状态量
针对本文的空间机器人系统能量最优路径规划问题,以自由漂浮空间三杆机械臂系统为例[27],给定系统初末端姿态
| $J=\frac{{{t}_{f}}-{{t}_{0}}}{2}\sum\limits_{i=0}^{3}{{{\left\| {{U}_{i}} \right\|}^{2}}}{{w}_{i}}$ | (39) |
最小,且满足如下离散的系统动态方程约束
| $\left. \begin{align} & \sum\limits_{i=0}^{N}{{{D}_{ki}}{{X}_{1i}}}=\frac{{{t}_{f}}-{{t}_{0}}}{2}{{U}_{1k}} \\ & \sum\limits_{i=0}^{N}{{{D}_{ki}}{{X}_{2i}}}=\frac{{{t}_{f}}-{{t}_{0}}}{2}{{U}_{2k}} \\ & \sum\limits_{i=0}^{N}{{{D}_{ki}}{{X}_{3i}}}=\frac{{{t}_{f}}-{{t}_{0}}}{2}{{U}_{3k}} \\ & \sum\limits_{i=0}^{N}{{{D}_{ki}}{{X}_{4i}}}=\frac{{{t}_{f}}-{{t}_{0}}}{2}\left( {{B}_{11}}{{U}_{1k}}+{{B}_{12}}{{U}_{2k}}+{{B}_{13}}{{U}_{3k}} \right) \\ & \sum\limits_{i=0}^{N}{{{D}_{ki}}{{X}_{5i}}}=\frac{{{t}_{f}}-{{t}_{0}}}{2}\left( {{B}_{21}}{{U}_{1k}}+{{B}_{22}}{{U}_{2k}}+{{B}_{23}}{{U}_{3k}} \right) \\ & \sum\limits_{i=0}^{N}{{{D}_{ki}}{{X}_{6i}}}=\frac{{{t}_{f}}-{{t}_{0}}}{2}\left( {{B}_{31}}{{U}_{1k}}+{{B}_{32}}{{U}_{2k}}+{{B}_{33}}{{U}_{3k}} \right) \\ \end{align} \right\}$ | (40) |
其中
| $\left| {{U}_{ik}} \right|\le {{U}_{\max }}$ | (41) |
式中
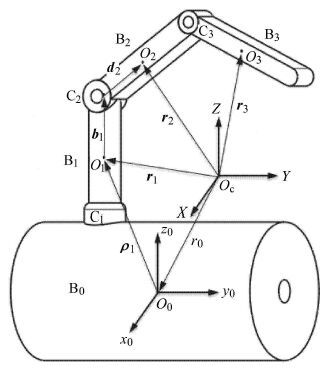
以6自由度空间自由漂浮机器人系统作为算例,设系统为航天器载体B0和三杆机械臂Bi (i = 1,2,3)以圆柱铰Ci (i = 1,2,3)联接组成(见图 3).图中
|
图 3 带空间机械臂的刚体航天器简图 Fig.3 Rigid spacecraft with space manipulators diagram |
航天器载体姿态由Cayley参数
| $\dot{x}=\left[ \begin{matrix} {{E}_{3\times 3}} \\ -{{\Gamma }^{-1}}J_{0}^{-1}[{{J}_{1}}{{e}_{1}}{{J}_{2}}{{e}_{2}}{{J}_{3}}{{e}_{3}}] \\ \end{matrix} \right]u$ | (42) |
式中
给定机器人系统初始位形
| 表 1 空间机器人系统质量几何参数 Table 1 Geometric parameters of the space manipulator system |
算例1 设系统的初始位形和终端目标位形分别为
| $\begin{align} & {{x}_{0}}={{[-\pi /2-\pi /2-0.5-1-11]}^{\text{T}}} \\ & {{x}_{f}}={{[\pi /2-\pi /2-0.5-1-11]}^{\text{T}}} \\ \end{align}$ |
空间机械臂与载体相连的第一杆件由初始位形
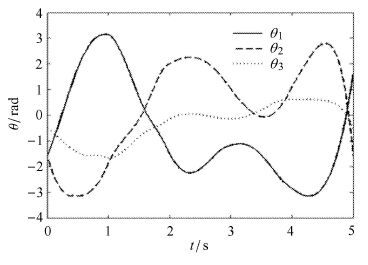
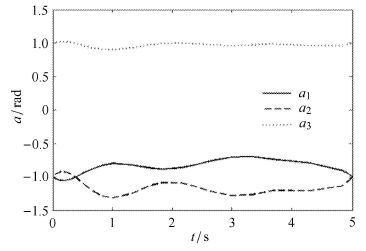
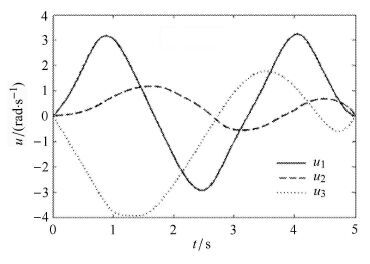
仿真结果如图 4 -图 6所示,其中图 4为空间机械臂关节角从初始位形转动到终端目标位形的优化轨迹,图 5为航天器载体从初始位形到终端目标位形姿态运动优化轨迹,图 6为空间机械臂关节相对转动的最优控制输入规律.
|
图 4 空间机械臂关节角运动优化轨迹 Fig.4 Space manipulator joint angle motion optimization trajectory |
|
图 5 航天器载体姿态运动优化轨迹 Fig.5 Spacecraft attitude motion optimization trajectory |
|
图 6 空间机械臂最优控制输入规律 Fig.6 Optimal control input of space manipulator |
算例2 设空间机器人系统的机械臂初始位形和终端目标位形保持不变,航天器载体由初始姿态
| $\begin{align} & {{x}_{0}}={{[-\pi /2-\pi /2-0.51-1-1]}^{\text{T}}} \\ & {{x}_{f}}={{[-\pi /2-\pi /2-0.5111]}^{\text{T}}} \\ \end{align}$ |
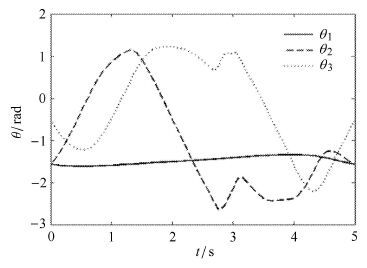
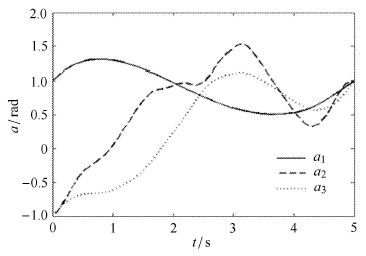
仿真结果如图 7 -图 9所示,其中图 7为空间机械臂关节角运动的优化轨迹,图 8为航天器载体姿态运动优化轨迹,图 9为空间机械臂关节的最优控制输入规律.
|
图 7 空间机械臂关节角运动优化轨迹 Fig.7 Space manipulator joint angle motion optimization trajectory |
|
图 8 航天器载体姿态运动轨迹 Fig.8 Spacecraft attitude motion optimization trajectory |
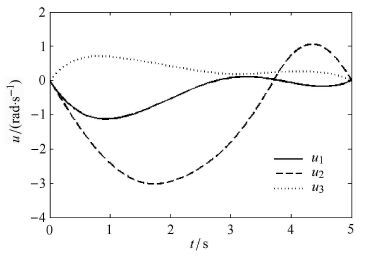
|
图 9 空间机械臂最优控制输入规律 Fig.9 Optimal control input of space manipulator |
上述仿真算例中,设置最大控制输入
(1) 应用Legendre 伪谱法求解了空间机器人的最优路径规划问题.在已知系统初末位形的情况下,文中以机械臂关节最小能量为待优化目标函数,同时考虑实际应用中的控制输入受限,将空间机器人的最优路径规划问题离散化为非线性参数规划问题,从而应用成熟的非线性规划算法进行求解.
(2) 伪谱法通过对系统状态空间和最优空间的全局逼近,将状态变量和控制变量同时离散为一组未知参数,使得非线性规划问题的未知量数目较多.但考虑到伪谱法可以利用少量的节点而获得"谱精度",因此在获得同等精度条件下,Legendre 伪谱法的未知量的个数要远小于基于有限元配置的直接法,使得Legendre伪谱法的计算速度和计算精度都要优于传统的基于有限元配置的直接法.
(3) 本文的结果主要针对非完整系统模型,应用伪谱法得到的自由漂浮空间机器人最优路径能够较好地满足各种约束条件,并具有精度较高和计算速度快的优点,为解决非完整运动规划问题提供了一条新的途径.
| [1] |
Dubowsky S, Papadopoulos E. The kinematics, dynamics, and control of free-flying and free-floating space robotic systems[J].
IEEE Transactions on Robotics and Automation,1993, 9 (5) : 531-542.
DOI: 10.1109/70.258046. ( 0) 0)
|
| [2] |
Krishman S. Vadali SR. Optimal rotational maneuvers of spacecraft using manipulator arms. Proc. of AIAA Conference on Guidance, Navigation and Control, 1994
( 0) 0)
|
| [3] |
Yamada K, Yoshikawa S. Feedback control of space robot attitude by cyclic arm motion[J].
Journal of Guidance,Control,and Dynamics,1997, 20 (4) : 715-720.
DOI: 10.2514/2.4102. ( 0) 0)
|
| [4] |
Nakamura Y, Mukherjee R. Nonholonomic path planning of space robots via a bi-directional approach[J].
IEEE Transactions on Robotics and Automation,1991, 7 (4) : 500-514.
DOI: 10.1109/70.86080. ( 0) 0)
|
| [5] |
刘延柱, 顾晓勤. 空间机械臂逆动力学的Liapunov 方法[J].
力学学报,1996, 28 (5) : 558-563.
( Liu Yanzhu, Gu Xiaoqin. The Liapunov method for the inverse dynamics of a space manipulator[J].
Acta Mechanica Sinica,1996, 28 (5) : 558-563.
(in Chinese) ) ( 0) 0)
|
| [6] |
Coverstone VL, Wilkey NM. Optimal control of a satellite-robot system using direct collocation with non-linear programming[J].
Acta Astronautica,1995, 36 (3) : 149-162.
DOI: 10.1016/0094-5765(95)00096-I. ( 0) 0)
|
| [7] |
Cerven WT, Coverstone VL. Optimal reorientation of multibody spacecraft through joint motion using averaging theory[J].
Journal of Guidance,Control,and Dynamics,2001, 24 (4) : 788-795.
DOI: 10.2514/2.4779. ( 0) 0)
|
| [8] |
Fenandes C, Gurvits L, Li ZX. Attitude control of a space platform/manipulator system using internal motion[J].
The Inter Journal of Robotics Research,1994, 13 (4) : 289-304.
DOI: 10.1177/027836499401300401. ( 0) 0)
|
| [9] |
Rui C, Kolmanovsky IV, McClamroch NH. Nonlinear attitude and shape control of spacecraft with articulated appendages and reaction wheels[J].
IEEE Transactions on Automatic Control,2000, 45 (8) : 1455-1469.
DOI: 10.1109/9.871754. ( 0) 0)
|
| [10] |
王景, 刘良栋. 双臂空间机器人利用内部运动的姿态控制[J].
宇航学报,2000, 21 (1) : 28-35.
( Wang Jing, Liu Liangdong. Attitude control of dual-arm space robot using internal control[J].
Journal of Astronautics,2000, 21 (1) : 28-35.
(in Chinese) ) ( 0) 0)
|
| [11] |
赵晓东, 王树国, 严艳军, 等. 基于轨迹规划的自由漂浮空间机器人抓取运动物体的研究[J].
宇航学报,2002, 23 (3) : 48-51.
( Zhao Xiaodong, Wang Shuguo, Yan Yanjun, et al. Algorithm of capturing at a moving body for a free-floating space manipulator based on trajectory planning[J].
Journal of Astronautics,2002, 23 (3) : 48-51.
(in Chinese) ) ( 0) 0)
|
| [12] |
Ge XS, Chen LQ, Liu YZ. Optimal control of the deployment process of solar wings on spacecraft[J].
Acta Astronautics,2007, 60 (8) : 684-690.
( 0) 0)
|
| [13] |
戈新生, 孙鹏伟. 自由漂浮空间机械臂的非完整运动规划粒子群优化算法[J].
机械工程学报,2007, 43 (4) : 34-38.
DOI: 10.3901/JME.2007.04.034. ( Ge Xinsheng, Sun Pengwei. Nonholonmic motion planning of space manipulator system using particle swarm optimization[J].
Chinese Journal of Mechanical Engineering,2007, 43 (4) : 34-38.
(in Chinese) DOI: 10.3901/JME.2007.04.034. ) ( 0) 0)
|
| [14] |
Elnagar G, Kazemi MA, Razzaghi M. The pseudospectral Legendre method for discretizing optimal control problems[J].
IEEE Trans on Automatic Control,1995, 40 (10) : 1793-1796.
DOI: 10.1109/9.467672. ( 0) 0)
|
| [15] |
Fahroo F, Ross IM. Costate estimation by a Legendre pseudospectral method[J].
Journal of Guidance,Control and Dynamics,2001, 24 (2) : 270-277.
DOI: 10.2514/2.4709. ( 0) 0)
|
| [16] |
Ross IM, Fahroo F. Pseudospectral knotting methods for solving optimal control problem[J].
Journal of Guidance,Control and Dynamics,2004, 27 (3) : 397-405.
DOI: 10.2514/1.3426. ( 0) 0)
|
| [17] |
Rao AV, Clarke KA. Performance optimization of a maneuvering re-entry vehicle using a legendre pseudospectral method. 2002 AIAA Atmospheric Flight Mechanics Conference, AIAA Paper 2002-4885, Monterey, CA August 5–8, 2002
( 0) 0)
|
| [18] |
Huntington GT, Rao AV. Optimal reconfiguration of spacecraft formations using the gauss pseudospectral method[J].
Journal of Guidance, Control,and Dynamics,2012, 31 (3) : 689-698.
( 0) 0)
|
| [19] |
雍恩米, 唐国金, 陈磊. 基于Gauss 伪谱方法的高超声速飞行器再入轨迹快速优化[J].
宇航学报,2008, 29 (6) : 1766-1772.
( Yong Enmi, Tang Guojin, Chen Lei. Rapid trajectory optimization for hypersonic reentry vehicle via gauss pseudospectral method[J].
Journal of Astronautics,2008, 29 (6) : 1766-1772.
(in Chinese) ) ( 0) 0)
|
| [20] |
Li S, Duan GR. A pseudospectral method for trajectory optimization of free-floating space manipulator[J].
Chinese Control Conference,2012 : 2395-2399.
( 0) 0)
|
| [21] |
Duan GR, Li S. FFSM trajectory optimization via multiphase Gauss pseudospectral method[J].
The 10th World Congress on Intelligent Control and Automation,2012 : 1615-1620.
( 0) 0)
|
| [22] |
廖一寰, 李道奎, 唐国金. 基于混合规划策略的空间机械臂运动规划研究[J].
宇航学报,2011, 32 (1) : 98-103.
( Liao Yihuan, Li Daokui, Tang Guojin. Motion planning of space manipulator system based on a hybrid programming strategy[J].
Journal of Astronautics,2011, 32 (1) : 98-103.
(in Chinese) ) ( 0) 0)
|
| [23] |
Liao YH, Li DK, Tang GJ. Motion planning for vibration reducing of free-floating redundant manipulators based on hybrid optimization approach[J].
Chinese Journal of Aeronautics,2011, 24 (4) : 533-540.
DOI: 10.1016/S1000-9361(11)60062-9. ( 0) 0)
|
| [24] |
刘延柱, 潘振宽, 戈新生.
多体系统动力学[M]. 北京: 高等教育出版社, 2014 .
( Liu Yanzhu, Pan Zhenkuan, Ge Xinsheng.
Dynamics of Multibody Systems[M]. Beijing: Higher Education Press, 2014 .
(in Chinese) ) ( 0) 0)
|
| [25] |
Shuster MD. A survey of attitude representations[J].
Journal of Astronautics Science,1993, 41 (4) : 439-518.
( 0) 0)
|
| [26] |
Hull DG.
Optimal Eontrol Theory for Applications[M]. New York: Springer-Verlag, 2003 .
( 0) 0)
|
| [27] |
戈新生. 多体航天器姿态运动建模和非完整运动控制. [博士论文]. 上海: 上海大学, 2004: 114-121
( Ge Xinsheng. Multibody spacecraft modelling of attitude motion and nonholonomic motion planning. [PhD Thesis]. Shanghai: Shanghai University, 2004: 114-121(in Chinese)
) ( 0) 0)
|
2. School of Mechanical & Electrical Engineering, Beijing Information Science & Technology University, Beijing 100192, China
 2016, Vol. 48
2016, Vol. 48